↗ OpenReview ↗ NeurIPS Homepage ↗ Hugging Face ↗ Chat
TL;DR#
Scaling up large language models (LLMs) is crucial for improved performance but comes with the challenges of increased computational costs. Mixture of Experts (MoE) models offer a solution by distributing the computational workload across multiple experts, but existing MoE models have limitations such as discontinuity and instability. These factors limit their efficiency and scalability.
This paper introduces a novel approach called Mixture of Tokens (MoT). Unlike traditional MoE, MoT adopts a continuous architecture that mixes tokens from different examples to each expert. This approach ensures full compatibility with autoregressive decoding and offers improved training stability and efficiency. The experiments demonstrate a 3x increase in training speed compared to dense transformer models, while maintaining state-of-the-art performance. The method also demonstrates a novel transition tuning method that allows for fine-tuning a pre-trained MoT model for use with sparse MoE inference.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with large language models (LLMs) due to its focus on improving training efficiency and scalability. The proposed Mixture of Tokens (MoT) architecture offers a novel approach to overcome the limitations of existing Mixture of Experts (MoE) models. By introducing a continuous MoE design, MoT achieves significant speedups in training while maintaining state-of-the-art performance. This opens up new avenues for research on optimizing LLM training and for developing more efficient and scalable LLMs for various applications. The transition tuning technique further enhances the practical applicability of MoT by providing a pathway for adapting MoT-trained models to sparse MoE inference.
Visual Insights#
The figure illustrates the Mixture of Tokens architecture. Tokens from different examples are grouped, and each group is processed by a set of experts. Each expert receives a weighted mixture of tokens, determined by a controller (not shown for clarity). The output of each expert is a weighted combination that contributes to the final token updates. This design allows for scaling parameters without proportionally increasing computation.

This table compares the training loss of MoT-Medium/32E and Expert Choice-Medium/32E models using mixed precision and bfloat16 precision. It shows that MoT achieves lower loss, especially in the bfloat16-only setting, indicating greater robustness to lower precision training. Learning rates were optimized separately for each model and precision level.
In-depth insights#
Cont. MoE via Tokens#
The concept of “Cont. MoE via Tokens” presents a novel approach to Mixture of Experts (MoE) models. It tackles the limitations of existing continuous MoE methods, which often lag behind sparse MoEs in performance or lack compatibility with autoregressive decoding. The core innovation lies in how it handles token processing. Instead of routing individual tokens to experts, it groups tokens from different examples and feeds these combined representations to each expert. This clever design, enabling continuous model behavior and full compatibility with autoregressive training and generation, simultaneously increases parameter count without a corresponding increase in FLOPs, similar to sparse MoEs. The elimination of the discrete top-k selection process, a significant source of instability in sparse MoEs, promotes smoother training and enhanced stability. Furthermore, a notable finding is the architectural connection between this method and traditional MoEs, demonstrated via a “transition tuning” technique, showcasing adaptability and flexibility. This approach promises improved efficiency and scalability in training large language models, offering a compelling alternative to existing MoE architectures.
Scaling MoT Models#
Scaling Mixture of Tokens (MoT) models involves exploring how efficiently the model’s capacity can be increased without proportionally increasing computational cost. This is achieved by adjusting key architectural parameters like the number of experts, the size of each expert, and the number of tokens per group. Increasing the number of experts allows for greater specialization and can improve model performance, but also increases the computational load. Reducing expert size while simultaneously increasing their number offers a potential solution, enabling more parameters without a proportional increase in FLOPs per token. Adjusting the number of tokens per group allows a trade-off between computational efficiency and the richness of the information each expert processes. Understanding the interplay of these parameters is crucial for optimizing scaling. Furthermore, investigating the effects of different precision levels (e.g., bfloat16) on scaling is vital, as it impacts training speed and stability. Finally, a comprehensive evaluation framework should assess the effects of scaling on both training time and downstream task performance. This multifaceted analysis will unveil the optimal scaling strategies for MoT models, paving the way for developing larger, more powerful, and efficient language models.
MoT Training Speed#
The Mixture of Tokens (MoT) architecture demonstrates a significant advantage in training speed compared to traditional dense Transformer models. MoT achieves a 3x speedup in language pretraining, showcasing its efficiency in processing large datasets. This improvement stems from MoT’s unique approach of mixing tokens from different examples before feeding them to expert networks. This strategy decouples parameter count from computational cost, allowing for scaling without a proportional increase in FLOPs (floating-point operations). Unlike sparse MoE methods which suffer from discontinuities and instability, MoT’s continuous nature contributes to its enhanced training stability and speed. The efficient vectorized implementation further contributes to the speed gains. The results suggest that MoT’s continuous design and token mixing strategy are key factors contributing to its superior training efficiency when compared to both dense Transformers and even existing sparse MoE architectures.
Transition Tuning#
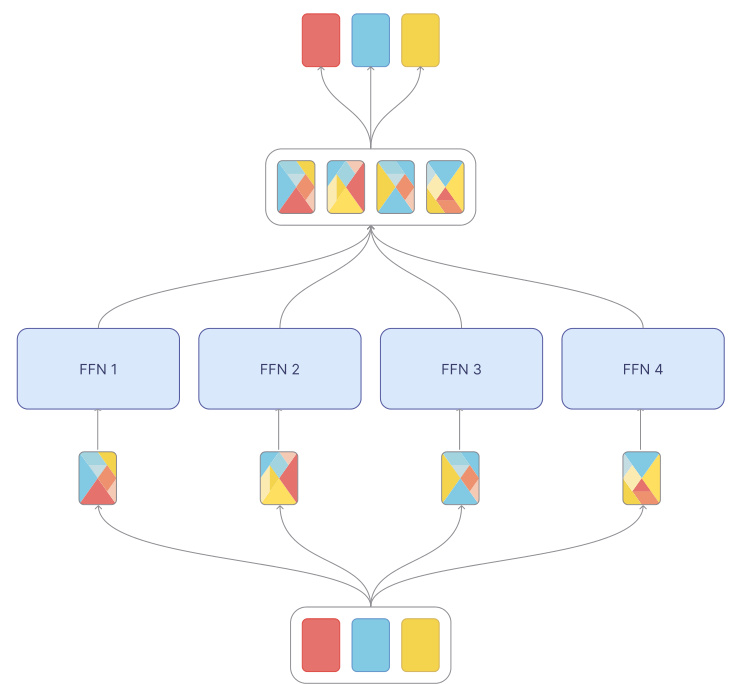
The heading ‘Transition Tuning’ highlights a crucial contribution of the research: bridging the gap between the efficient training of Mixture of Tokens (MoT) models and the requirement for unbatched inference, often necessary for deployment on resource-constrained devices. MoT’s inherent batch processing limits its direct applicability in scenarios demanding individual token processing. Transition tuning cleverly addresses this by leveraging the knowledge gained during MoT’s training to initialize a sparse MoE model. This initialization jumpstarts the training of the sparse MoE, significantly reducing the required training time. This technique essentially allows for a smooth transition from the computationally advantageous training phase of MoT to the deployment-friendly inference phase of sparse MoE. The effectiveness of transition tuning is demonstrated experimentally, achieving comparable performance to fully trained sparse MoE models with considerably less computational effort. This is a significant step toward making the benefits of MoT accessible in real-world applications, where the constraints of batched inference might be prohibitive. The technique showcases a practical approach to transfer learning between different MoE architectures, offering valuable insights into the relationship between continuous and sparse MoE models. It potentially opens avenues for exploring similar transfer mechanisms within other model architectures, paving the way for more adaptable and versatile deep learning systems.
MoT Limitations#
The Mixture of Tokens (MoT) architecture, while demonstrating significant improvements in training speed and performance, presents certain limitations. Its reliance on batched inference restricts its applicability in scenarios requiring individual token processing, hindering its use in certain applications. The computational cost associated with large-scale models, although improved over sparse MoE methods, remains a barrier to widespread adoption. While MoT exhibits greater stability during low-precision training than sparse MoE, further investigation into its robustness across varied model sizes is necessary. Finally, the lack of detailed analysis on the impact of token mixing on model performance warrants additional research to fully understand the intricacies of this novel approach. Addressing these limitations will be crucial for maximizing MoT’s potential and broadening its applications.
More visual insights#
More on figures
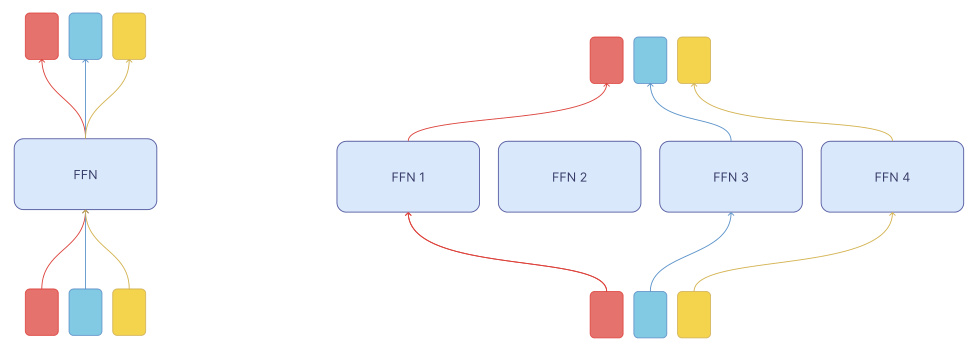
The figure illustrates the difference between a standard Feed-Forward layer in a Transformer and a Token Choice layer in a Mixture of Experts model. In the standard Feed-Forward layer, each token is processed independently by the same Multi-Layer Perceptron (MLP). In contrast, the Token Choice layer allows each token to choose an expert to process it. This creates sparsity as not all experts are utilized for every token, and if an expert is overloaded, some tokens might be dropped, resulting in unequal treatment of tokens and potential training instability.
This figure shows how tokens are grouped in Mixture of Tokens (MoT). Tokens from different sequences are grouped together, and each group contains tokens that occupy the same position within their respective sequences. The size of these groups influences the number of experts used, maintaining a balance between model size and computational efficiency. The maximum group size is limited by the batch size.
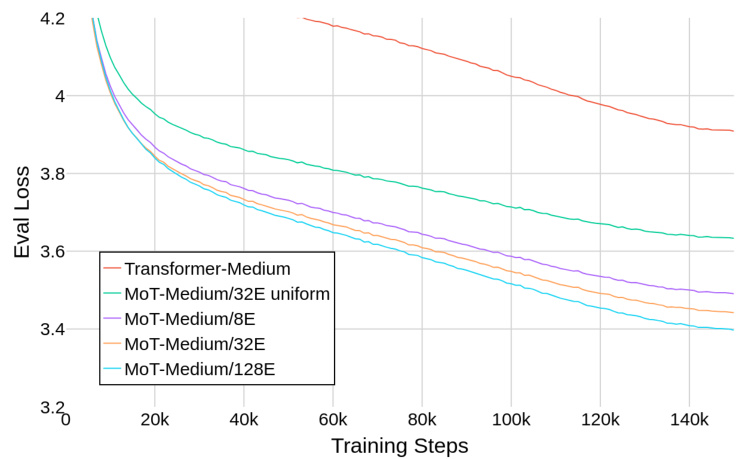
The figure shows the evaluation loss for different models during training, plotted against the number of training steps. The models compared include a standard Transformer-Medium model and several Mixture of Tokens (MoT) models with varying numbers of experts (8, 32, 128). An additional MoT model with a uniform (non-learnable) routing strategy is also included for comparison. The plot demonstrates the scaling properties of MoT models, showing that increasing the number of parameters (by increasing the number of experts) consistently improves performance, exceeding that of the standard Transformer model.
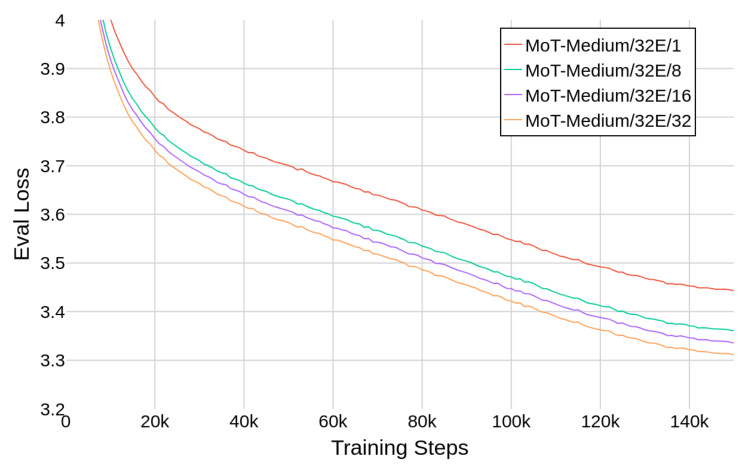
The figure shows how the model’s evaluation loss changes as the number of token mixtures per expert increases during training. Different lines represent models with varying numbers of mixtures (1, 8, 16, and 32). The results demonstrate that increasing the number of mixtures consistently improves model performance, as indicated by a lower evaluation loss. This suggests that allowing each expert to process multiple mixtures of tokens enhances the model’s expressiveness and learning capabilities.
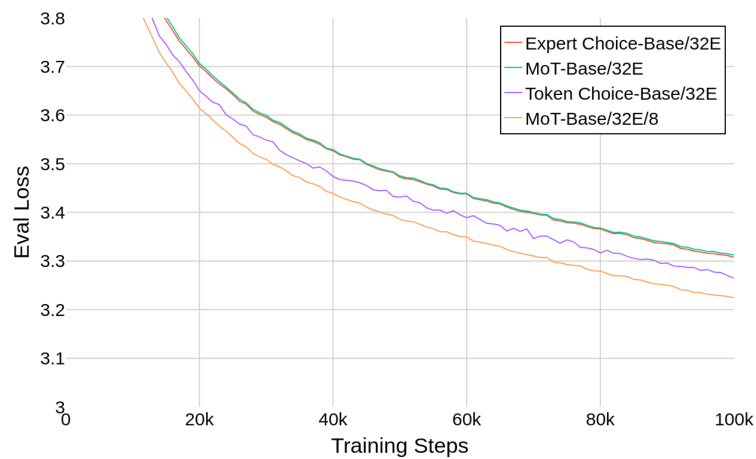
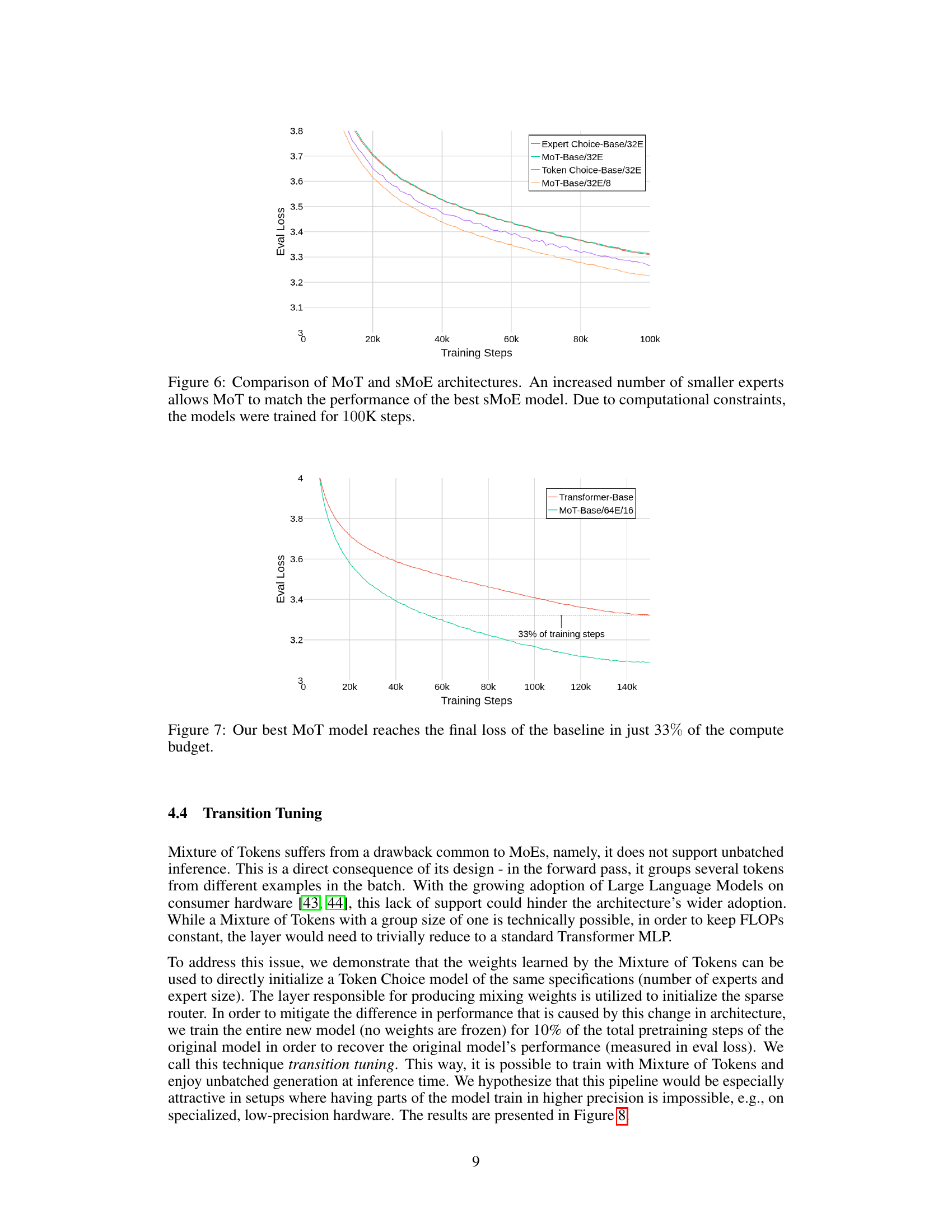
This figure compares the performance of Mixture of Tokens (MoT) against two state-of-the-art sparse Mixture of Experts (sMoE) models: Expert Choice and Token Choice. The results show that MoT, using a larger number of smaller experts, achieves comparable performance to the best-performing sMoE model. Due to limitations in computational resources, all models were trained for a reduced number of steps (100K).
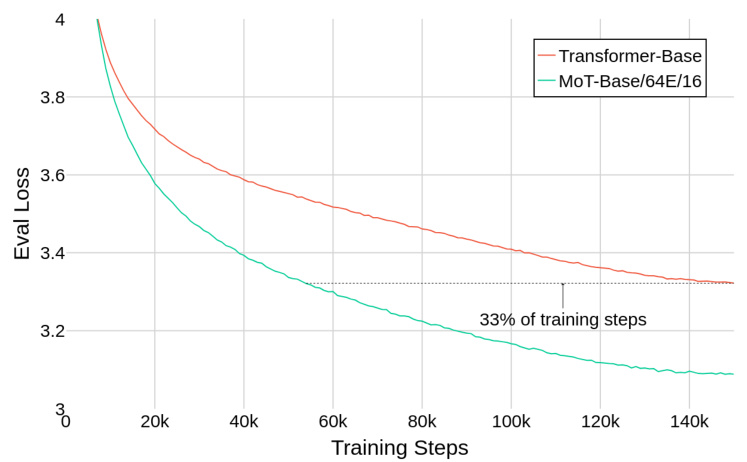
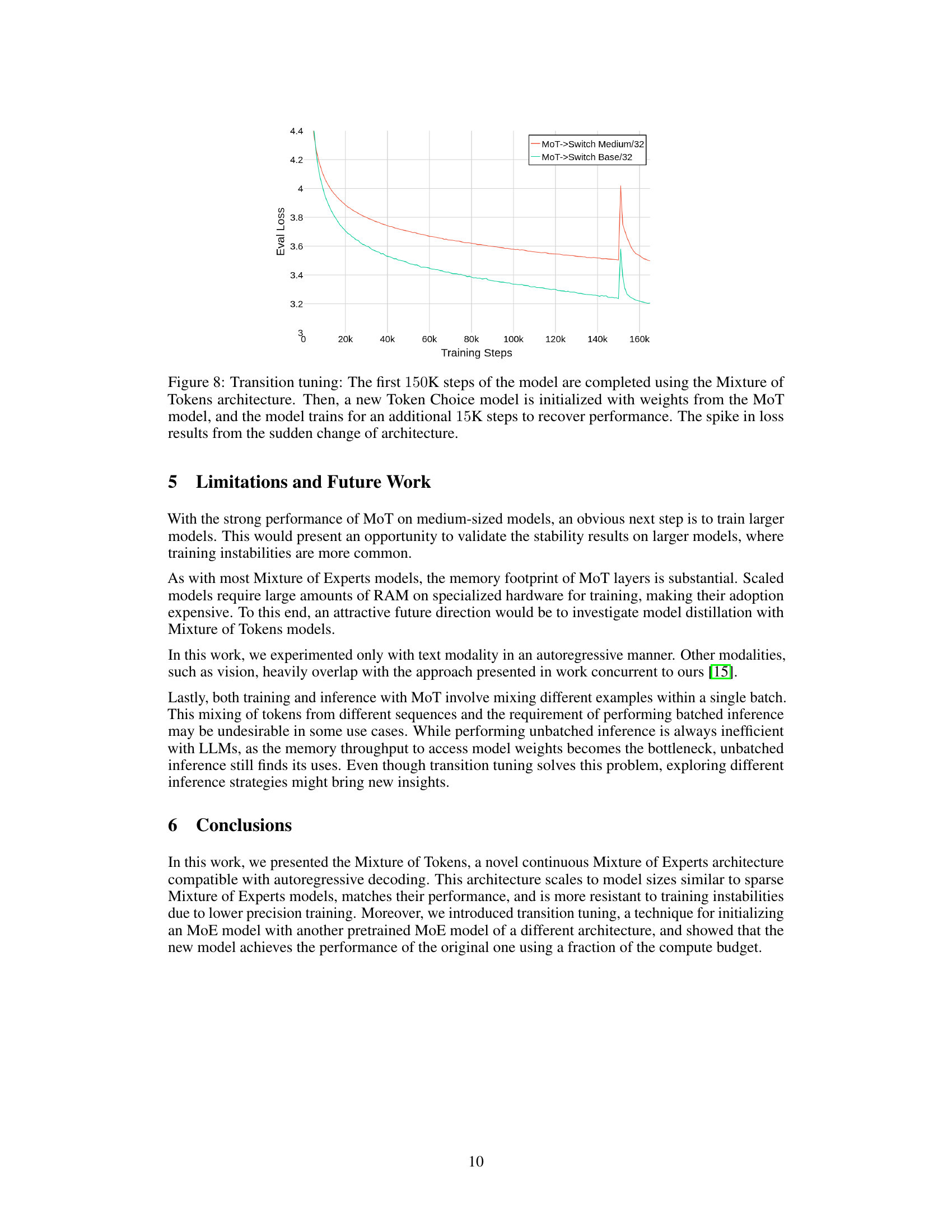
This figure shows a comparison of training curves between a standard Transformer-Base model and the best performing Mixture of Tokens (MoT) model from the paper. The y-axis represents the evaluation loss, and the x-axis represents the number of training steps. The MoT model achieves a similar final loss to the Transformer model but in significantly fewer training steps – approximately one-third the number of steps. This demonstrates the computational efficiency of the MoT architecture.

This figure shows the training loss curves for transition tuning. Two models, one medium-sized and one base-sized, are initially trained using the Mixture of Tokens (MoT) architecture for 150,000 steps. Then, these models are converted to Token Choice models (a type of sparse Mixture of Experts architecture). The weights from the MoT models are used to initialize the Token Choice models, and training continues for an additional 15,000 steps. The spike in loss at around 150,000 steps is attributed to the architecture switch.
More on tables

This table compares the training loss of MoT-Medium/32E and Expert Choice-Medium/32E models under two different precision settings: mixed precision and bfloat16 only. The results show that MoT exhibits lower training loss in both settings, and particularly demonstrates superior stability compared to Expert Choice when using bfloat16 precision only. The comparison highlights MoT’s robustness to lower precision training.
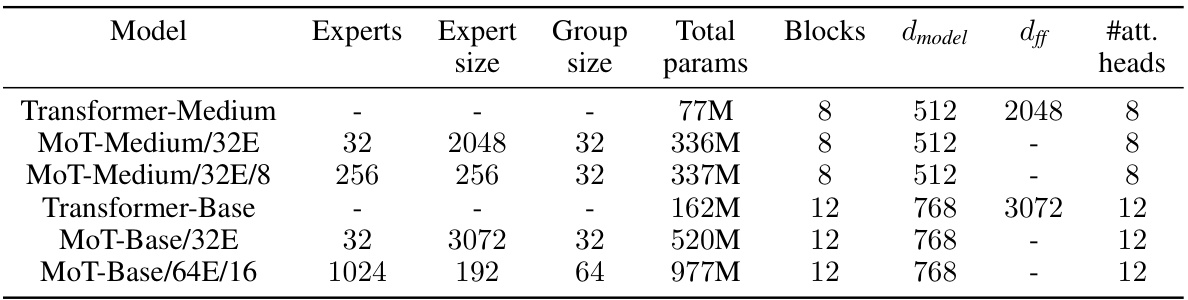
This table lists the hyperparameters used for training different models in the paper’s experiments. It shows the number of experts, expert group size, total parameters, number of blocks, d_model dimension, d_ff dimension (feed-forward network hidden units), and number of attention heads for each model configuration (Transformer-Medium, MoT-Medium/32E, MoT-Medium/32E/8, Transformer-Base, MoT-Base/32E, and MoT-Base/64E/16). This allows readers to reproduce the experiments.

This table presents the performance results of three different models—Transformer-Medium, MoT-Medium/32E/1, and MoT-Medium/32E/16—on three downstream benchmarks: PIQA, HellaSwag, and ARC-e. The results demonstrate the improved performance of the MoT models (especially MoT-Medium/32E/16) over the Transformer-Medium baseline in a zero-shot setting.
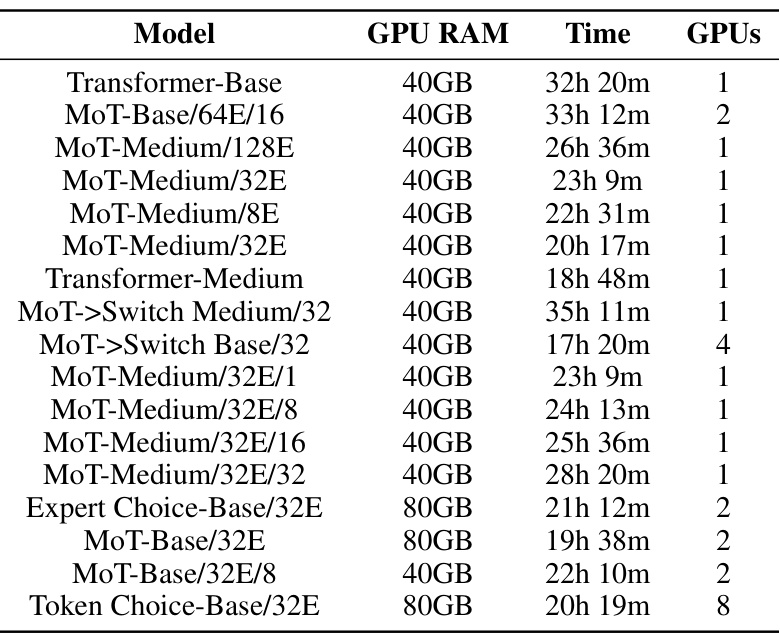
This table details the computational resources used for training different models mentioned in the paper. It shows the GPU RAM, training time, and number of GPUs used for each model. The models include various sizes of Transformers, MoT (Mixture of Tokens), and sparse MoE (Mixture of Experts) models.
Full paper#