Dense Associative Memory Through the Lens of Random Features

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is highly important for researchers working on associative memory and neural networks. It presents a novel approach to improve the scalability and efficiency of these models, which is a significant challenge in the field. The method has implications for various applications including pattern recognition and AI, opening up avenues for further research into more efficient and scalable memory systems.

Visual Insights

#

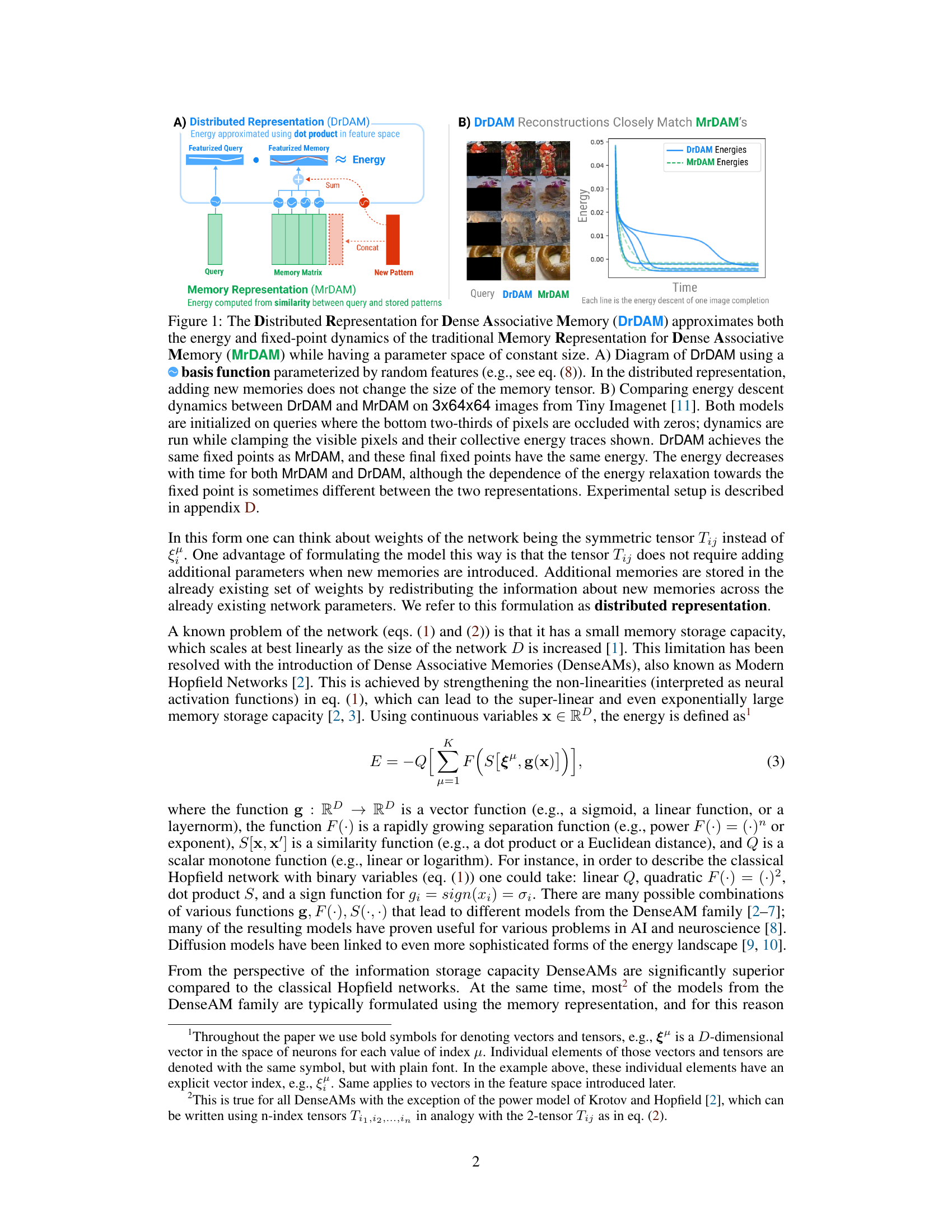
This figure compares two methods for dense associative memory: the traditional memory representation (MrDAM) and a new distributed representation (DrDAM) using random features. Part A illustrates the DrDAM architecture, showing how random features are used to approximate energy and how adding new memories doesn’t increase the number of parameters. Part B shows a comparison of energy descent dynamics for both methods on image completion tasks, demonstrating that DrDAM closely approximates MrDAM’s behavior.

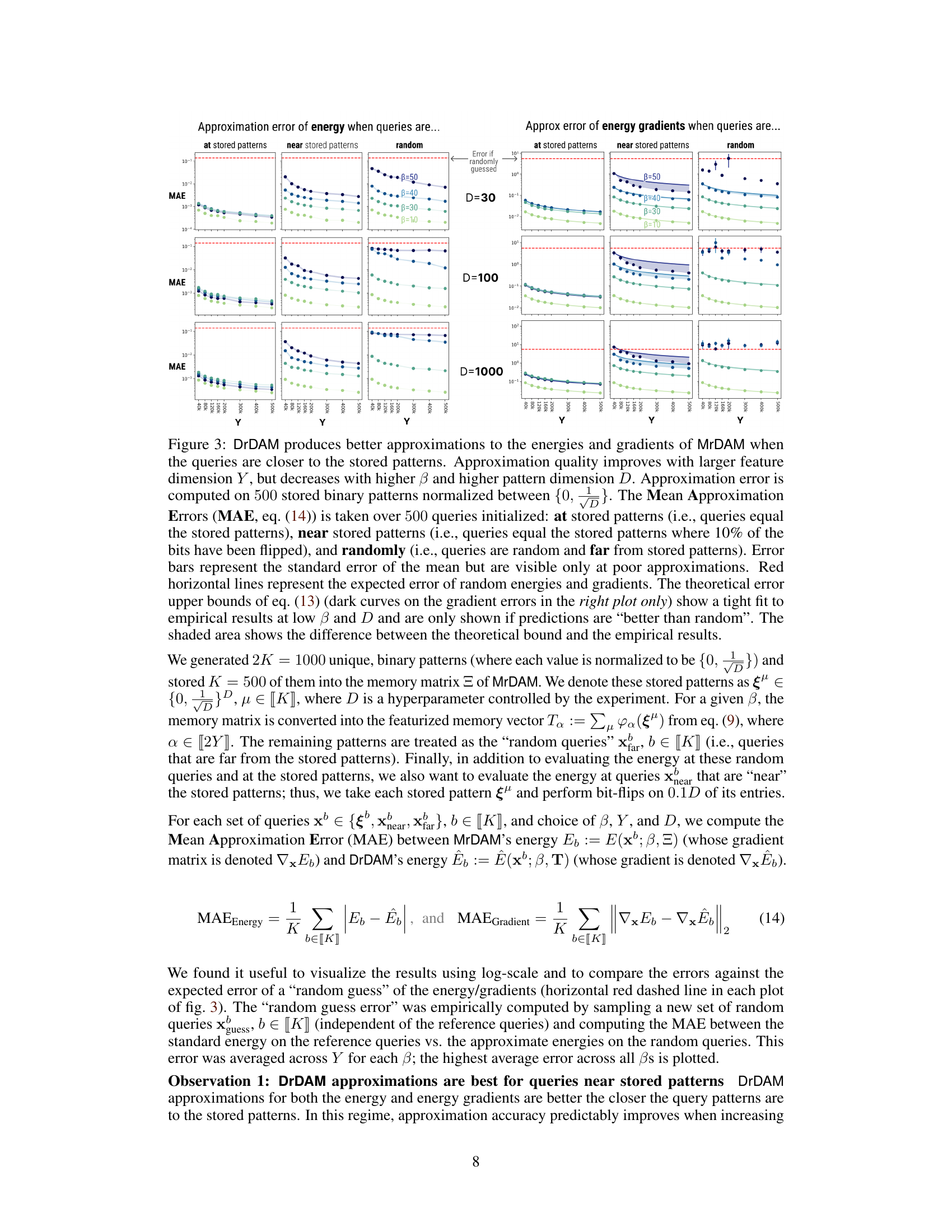
This figure shows the approximation errors of DrDAM compared to MrDAM for energy and gradients under different conditions. The approximation error is evaluated on queries initialized at stored patterns, near stored patterns, and randomly. The results demonstrate that DrDAM performs better when queries are closer to the stored patterns. The approximation quality also improves with a larger feature dimension (Y) but decreases with higher inverse temperature (β) and pattern dimension (D). The figure includes error bars and a comparison to the expected error of random energies and gradients, along with theoretical error bounds.

In-depth insights

#

DrDAM: A New Model

#

DrDAM, as a novel model, presents a significant advancement in dense associative memory by leveraging random features. Its core innovation lies in approximating the energy landscape of traditional Dense Associative Memories (MrDAM) without the need for storing individual memories explicitly. This results in a fixed parameter space, irrespective of the number of stored memories, offering significant parameter efficiency and the ability to easily incorporate new memories. DrDAM achieves this by mapping the memory representation into a feature space, cleverly enabling the approximation of the energy function and its dynamics. While there are inherent approximation errors, especially with higher inverse temperatures and when queries are distant from stored memories, the model proves highly effective in retrieving stored patterns and its computational cost scales favorably. The theoretical analysis thoroughly examines the approximation error, providing valuable insights into its dependence on various parameters, such as the feature space dimensionality and the number of stored memories. The empirical results validate these theoretical findings, showcasing the effectiveness of DrDAM as a practical and efficient alternative to MrDAM.

Random Feature Map

#

Random feature maps offer a powerful technique for approximating kernel methods, particularly useful in high-dimensional spaces where explicit computation of kernel functions becomes intractable. The core idea is to randomly project high-dimensional data into a lower-dimensional space using a set of random features. These projections are designed such that the inner product of the projected data approximates the kernel function in the original high-dimensional space. This allows for significant computational savings since operations are now performed in the lower-dimensional feature space. The quality of approximation depends on several factors, including the choice of random features (trigonometric, exponential, etc.), the number of random features used, and the properties of the kernel function being approximated. Careful consideration of these factors is crucial to ensure that the approximation is sufficiently accurate for the downstream task. The trade-off between accuracy and computational efficiency becomes a critical design consideration. In essence, random feature maps transform a computationally complex non-parametric kernel method into a simpler, parameterizable model, making kernel methods applicable to larger datasets and higher-dimensional data.

Approximation Limits

#

The section on “Approximation Limits” would be crucial for assessing the practical applicability of the proposed DrDAM model. It should rigorously analyze the sources and magnitudes of approximation errors introduced by using random features to represent the energy landscape. This includes quantifying the error introduced in the energy function and its gradient, ideally with theoretical bounds to show how the approximation error scales with key parameters like the dimensionality of the data, the number of random features, and the number of stored memories. The analysis needs to distinguish between approximation errors that significantly impact the model’s performance (e.g., leading to incorrect fixed points) and those that are relatively benign. Furthermore, a discussion of the trade-off between approximation accuracy and computational efficiency is essential, as employing more random features reduces error but increases the computational cost. Finally, empirical validation demonstrating the approximation limits under various conditions would lend further credence to the theoretical analysis.

Empirical Evaluation

#

An empirical evaluation section in a research paper is crucial for validating theoretical claims. It should meticulously detail experimental setup, including datasets, parameters, and metrics. Transparency is key, with clear descriptions allowing for reproducibility. The evaluation should address multiple aspects, comparing the proposed method to existing baselines under various conditions. Robustness is vital, exploring the algorithm’s performance across different settings and potential failure modes. The analysis shouldn’t just present results; it needs insightful discussion, interpreting findings in the context of the hypothesis and limitations. Statistical significance should be carefully assessed and reported, as well as error analysis, ensuring that observed trends aren’t due to random chance. A well-executed empirical evaluation builds confidence in the research, establishing its practical value and highlighting potential limitations for future research. Visualization of the results (graphs, tables) is also important to facilitate understanding and communication of the findings.

Future Work

#

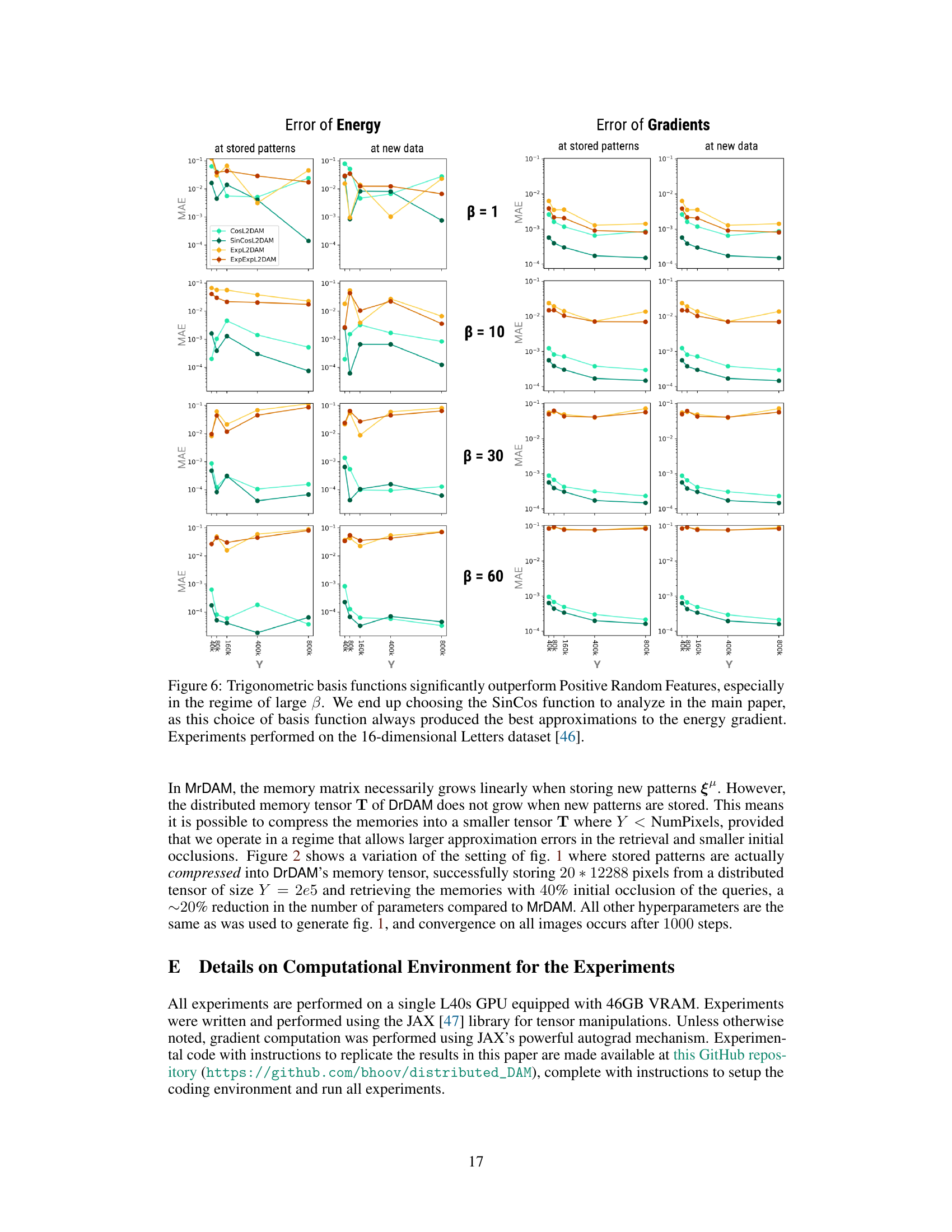
The paper’s ‘Future Work’ section could explore several promising avenues. Extending DrDAM to handle more complex data types beyond images and binary patterns is crucial. This would involve investigating appropriate kernel functions and random feature mappings for various modalities like text, audio, and sensor data. Furthermore, a thorough investigation into the effects of different random feature map choices is warranted. While SinCos is shown to perform well, other methods might offer better performance or greater scalability for specific applications. Developing a deeper theoretical understanding of the approximation error and its relationship to various hyperparameters (like inverse temperature β, feature dimensionality Y, and dataset characteristics) would strengthen the paper’s contributions. Finally, empirical validation on larger datasets and a broader range of tasks would solidify the claims of parameter efficiency and performance gains. In particular, a detailed comparison with state-of-the-art associative memory models is needed for conclusive evidence of DrDAM’s effectiveness. Integrating DrDAM into practical applications across diverse domains would showcase the model’s true capabilities.

More visual insights

#

More on figures

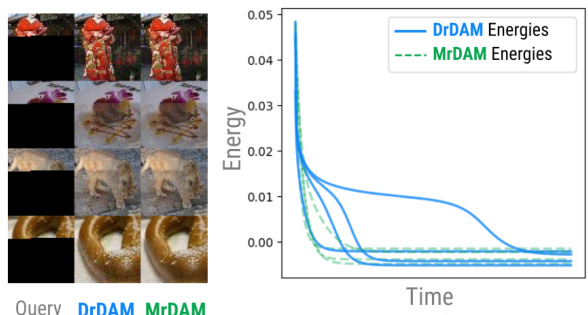
This figure demonstrates that the proposed DrDAM model effectively approximates both the energy and fixed-point dynamics of the traditional MrDAM model, while maintaining a constant parameter space size, regardless of the number of stored memories. Panel A shows a schematic of the DrDAM architecture using random features, while Panel B provides a comparison of the energy descent dynamics between DrDAM and MrDAM. The comparison shows that both models converge to the same fixed points with similar energy levels, even though the energy descent process itself can vary.

This figure compares the performance of DrDAM and MrDAM in storing and retrieving images from the TinyImagenet dataset. DrDAM demonstrates parameter compression by achieving similar retrieval accuracy with fewer parameters than MrDAM. The figure shows examples of occluded query images, the retrieved images from DrDAM, and the ground truth from MrDAM, highlighting the similarity between the two methods while demonstrating DrDAM’s reduced parameter count. The results suggest that DrDAM offers a more efficient way to store and recall images with minimal loss of accuracy.

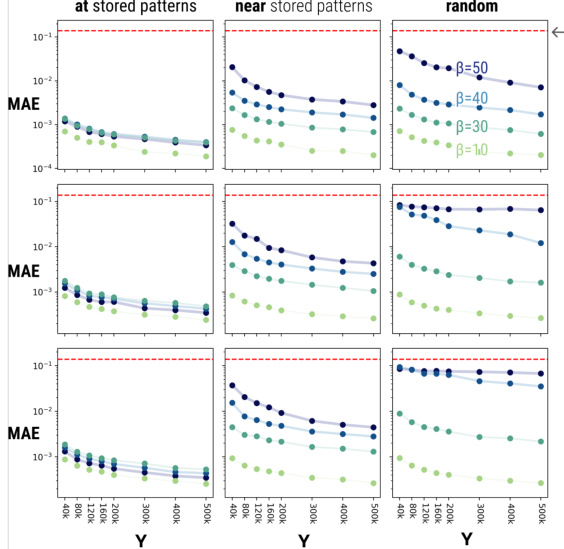
This figure shows the approximation error of DrDAM compared to MrDAM for energy and gradients. It demonstrates how well DrDAM approximates MrDAM’s energy and gradient under different conditions, considering queries at stored patterns, near stored patterns, and random queries. The results are shown for varying feature dimension (Y), inverse temperature (β), and pattern dimension (D). Error bars represent standard error of the mean. Red lines indicate the error of a random guess. The plot shows DrDAM performs better when queries are closer to stored patterns and that approximation quality improves with larger feature dimension (Y) but decreases with higher inverse temperature (β) and pattern dimension (D).

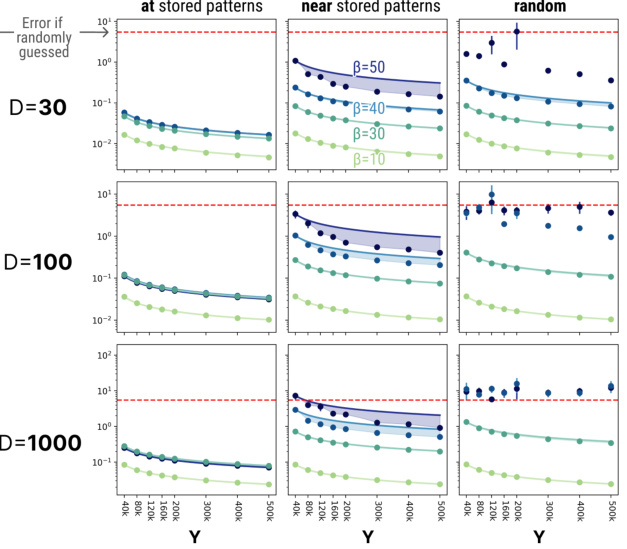
This figure analyzes the approximation quality of DrDAM compared to MrDAM under various conditions. It shows how the Mean Absolute Error (MAE) in energy and gradient approximations changes with the number of random features (Y), inverse temperature (β), and pattern dimension (D). Three scenarios are considered for query initialization: at stored patterns, near stored patterns (10% bit flips), and random queries. The figure includes error bars, theoretical error bounds, and a comparison against random guesses, providing a comprehensive assessment of DrDAM’s accuracy across diverse settings.

This figure shows the relationship between retrieval error, approximation quality, and hyperparameters (β and Y). Part A demonstrates how retrieval errors correlate with approximation quality from Figure 3, emphasizing the randomness of errors at high β and D. Part B visually demonstrates how DrDAM’s approximation quality improves with increasing Y, especially at lower β values, but requires larger Y for good approximations at higher β values. The experiment uses a corrupted CIFAR-10 image where the bottom half is masked, showing the fixed points of DrDAM and MrDAM for different β and Y values.

This figure shows the approximation errors of DrDAM compared to MrDAM for energy and gradients. It demonstrates that DrDAM’s accuracy is better when queries are close to stored patterns, increases with more features (Y), but decreases with higher inverse temperature (β) and dimensionality (D). The plots show MAE for three query types: at, near, and far from stored patterns. The results are compared to the expected error of random guesses and theoretical upper bounds.

Full paper

#