Learning to Shape In-distribution Feature Space for Out-of-distribution Detection

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working on out-of-distribution (OOD) detection because it introduces a novel framework that addresses the limitations of existing methods by deterministically shaping the in-distribution feature space during pre-training. This approach offers improved flexibility and generality, leading to state-of-the-art performance on various benchmarks. The theoretical framework and empirical results provide valuable insights and open up new avenues for research in this critical area of machine learning.

Visual Insights

#

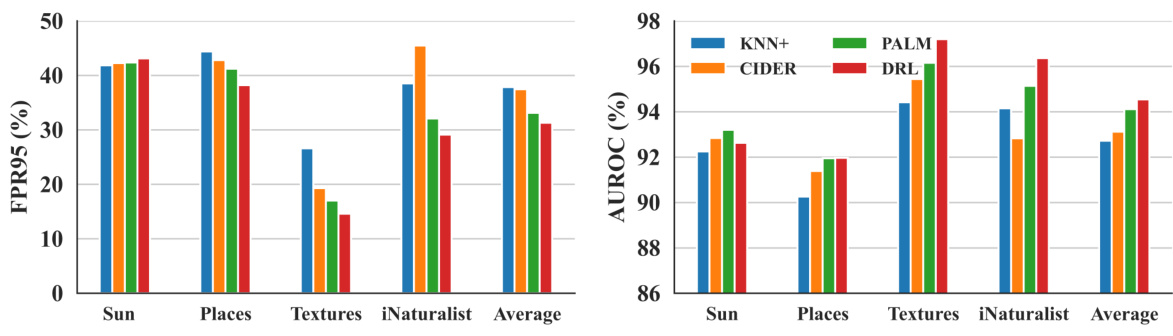
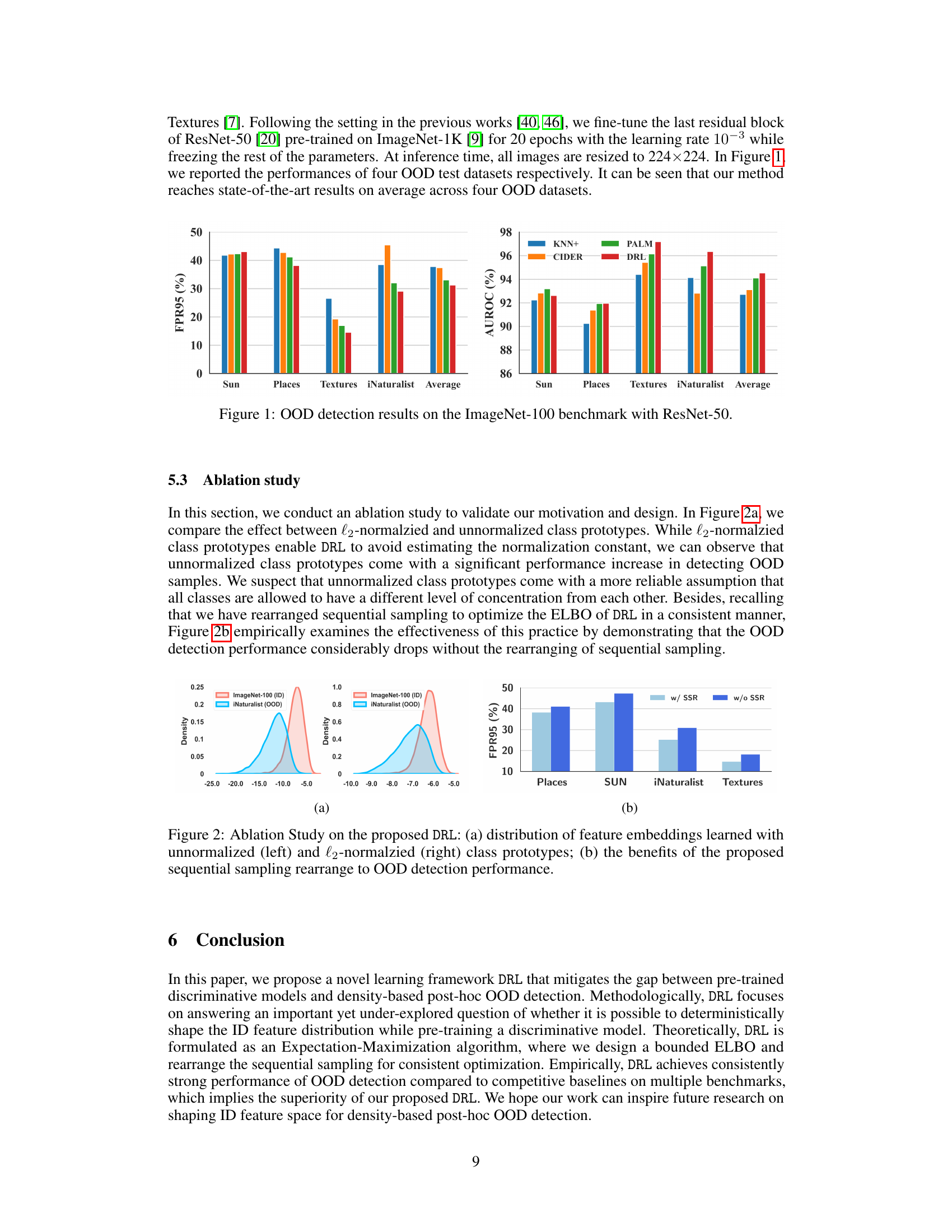
This figure presents a comparison of OOD detection performance on the ImageNet-100 benchmark using ResNet-50. The results show the FPR95 (False Positive Rate at 95% True Positive Rate) and AUROC (Area Under the Receiver Operating Characteristic curve) for four different OOD datasets (SUN, Places, Textures, iNaturalist) and the average performance across these datasets. Multiple methods are compared: KNN+, PALM, CIDER, and the proposed DRL method. The figure visually demonstrates the superior performance of the DRL method compared to the other methods, especially in terms of FPR95 (lower is better).

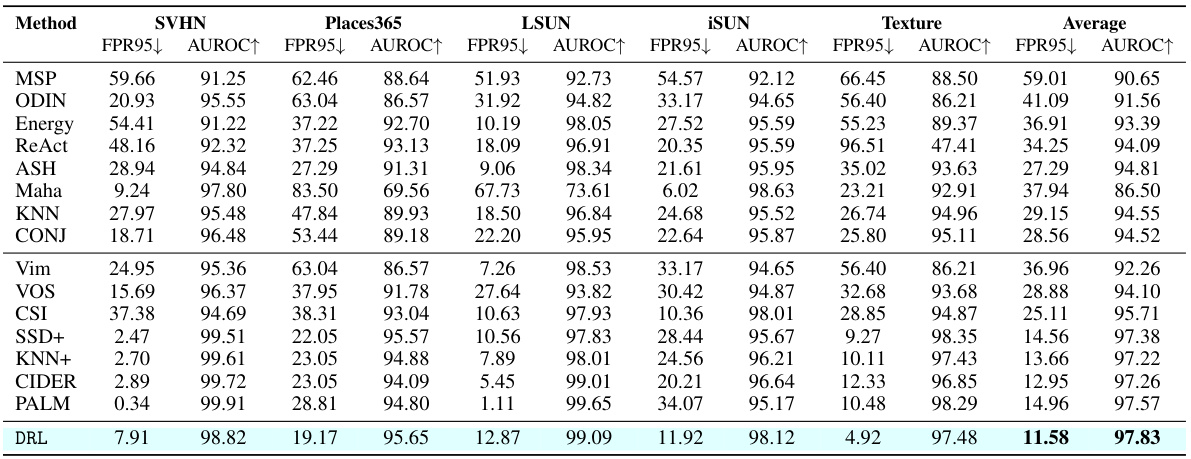
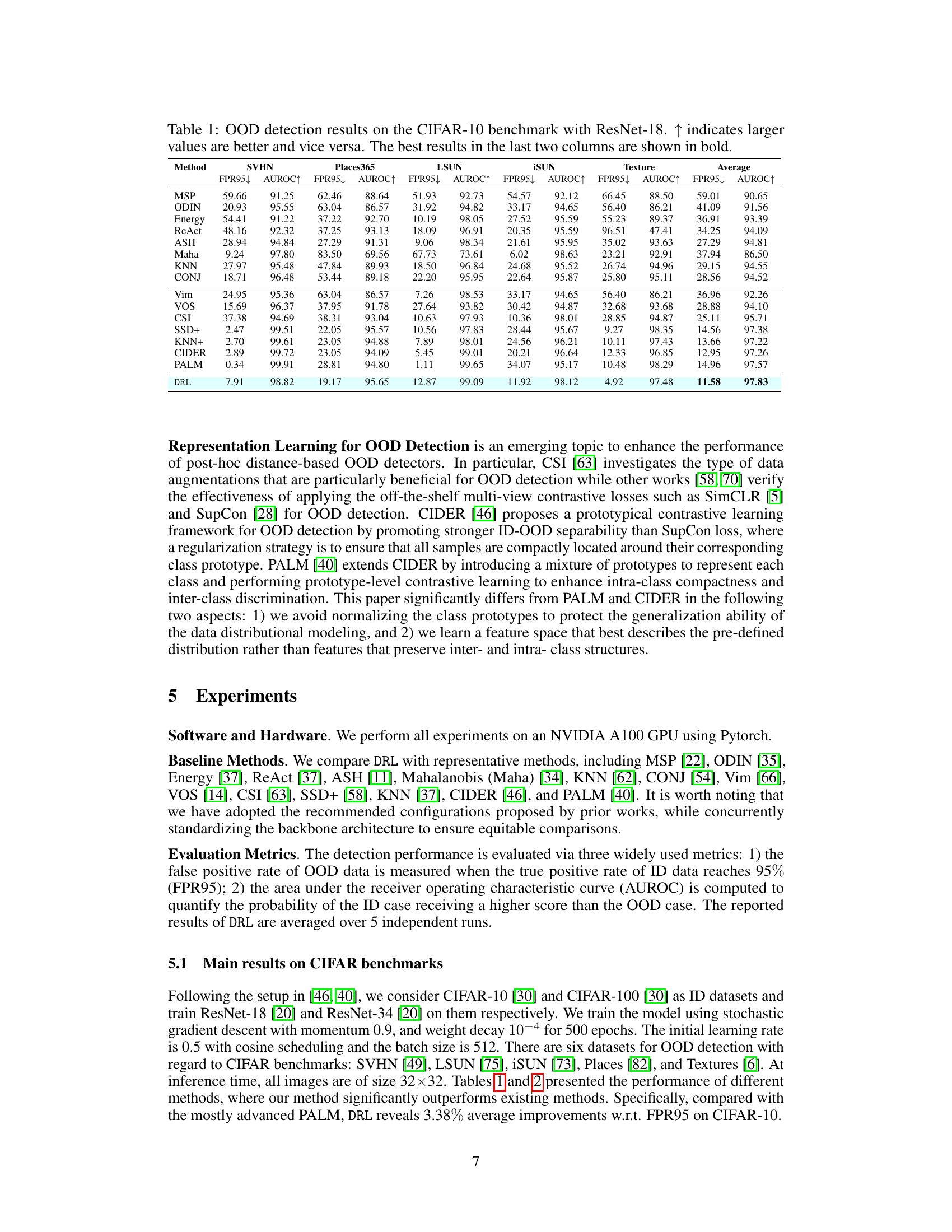
This table presents the out-of-distribution (OOD) detection performance of various methods on the CIFAR-10 dataset using a ResNet-18 model. The results are evaluated using two metrics: False Positive Rate at 95% True Positive Rate (FPR95) and Area Under the Receiver Operating Characteristic curve (AUROC). Lower FPR95 values and higher AUROC values indicate better performance. The table compares the proposed DRL method with several existing state-of-the-art OOD detection methods.

In-depth insights

#

OOD Detection

#

Out-of-distribution (OOD) detection is a crucial aspect of robust machine learning, addressing the challenge of model performance when encountering data differing significantly from training data. Existing methods often rely on strong distributional assumptions, either explicitly defining the in-distribution (ID) data’s characteristics or implicitly assuming a specific distribution in the learned feature space. This reliance poses a limitation as real-world data often deviates from these assumptions. A key focus of current research is moving beyond these rigid assumptions to develop more flexible and generalizable OOD detection techniques. This involves exploring techniques that learn and model the ID feature distribution directly during the model’s pre-training phase, eliminating the need for post-hoc analyses and the inherent inconsistencies between assumed and actual distributions. Furthermore, improving the accuracy of methods in hard OOD scenarios, where OOD data closely resembles ID data, is another crucial area of development. The pursuit of assumption-free and scalable solutions, along with a more theoretical understanding of OOD detectability, represents the future direction of research in this domain.

DRL Framework

#

A Distributional Representation Learning (DRL) framework for out-of-distribution (OOD) detection is proposed to address the limitations of existing methods that rely on strong distributional assumptions. DRL deterministically shapes the in-distribution (ID) feature space during pre-training, ensuring that the underlying distribution conforms to a pre-defined mixture model. This approach moves away from making explicit distributional assumptions about the feature space, offering increased flexibility and generality. An online approximation of normalization constants is employed to enable end-to-end training, addressing the computational challenges associated with conventional methods. Furthermore, DRL is formulated as a provably convergent Expectation-Maximization (EM) algorithm, preventing trivial solutions and enhancing training consistency via a strategic rearrangement of sequential sampling. This framework’s superior performance across various benchmarks underscores its ability to reliably model feature distributions and improve OOD detection accuracy.

EM Algorithm

#

The Expectation-Maximization (EM) algorithm is a powerful iterative method for finding maximum likelihood estimates of parameters in statistical models, especially when dealing with latent variables. Its core strength lies in its ability to handle situations where direct maximization is computationally intractable. The algorithm alternates between two steps: the Expectation (E-step), which computes the expected value of the complete-data log-likelihood given the observed data and current parameter estimates; and the Maximization (M-step), which maximizes this expected log-likelihood with respect to the parameters to obtain updated estimates. This iterative process continues until convergence, producing improved parameter estimates with each iteration. A crucial aspect of the EM algorithm’s effectiveness is its guaranteed convergence to a local maximum of the likelihood function, provided certain regularity conditions are satisfied. However, the algorithm’s convergence can be slow, and its final solution might be just a local rather than a global optimum. The choice of initial parameter values can significantly influence the algorithm’s convergence path and the final solution obtained. Therefore, careful consideration of initialization strategies is often crucial. Despite these limitations, the EM algorithm remains a versatile and widely-used tool in various machine learning and statistical applications, particularly in scenarios involving hidden or latent variables where direct parameter estimation is challenging.

Empirical Results

#

An ‘Empirical Results’ section in a research paper demands a thorough analysis. It should not simply present metrics; rather, a compelling narrative explaining the significance of findings is crucial. The discussion should connect results directly to the paper’s hypotheses and research questions. Careful consideration of baseline methods is essential to establish the novelty and improvement of the proposed approach. Visualizations, such as graphs and tables, can effectively communicate complex results, but clarity and concise labeling are critical. The writing style should be precise and avoid ambiguity, ensuring that the reader understands the methodology and implications of each experiment. Statistical significance should be explicitly addressed, and any limitations of the empirical study should be openly acknowledged.

Future Work

#

Future research could explore alternative distribution modeling techniques beyond the Gaussian mixture model used in this paper, potentially improving the accuracy and robustness of OOD detection. Investigating the effects of different latent feature space dimensions on the performance would be valuable. Furthermore, a thorough investigation into the sensitivity of the hyperparameters, especially the weighting factor between classification and ELBO, could reveal optimal settings for various datasets and tasks. Addressing the computational cost associated with online approximation of normalization constants, while maintaining accuracy, is crucial for scaling the approach to larger datasets. Finally, applying the DRL framework to other tasks beyond OOD detection such as anomaly detection or domain adaptation would provide insights into the broader applicability and impact of the approach. A direct comparison with recently proposed, more advanced methods in a unified evaluation setting would solidify the reported improvements.

More visual insights

#

More on figures

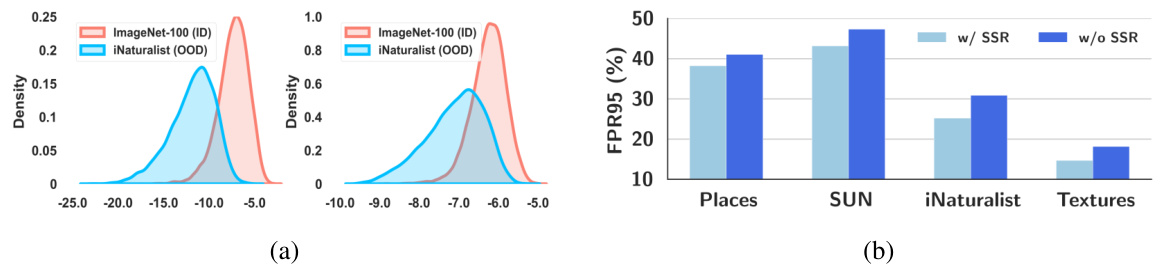
This figure presents an ablation study to support the claims made in the paper. The first sub-figure (a) compares the distribution of feature embeddings using unnormalized versus l2-normalized class prototypes. It shows that unnormalized prototypes lead to better OOD detection performance. The second sub-figure (b) demonstrates the impact of the proposed sequential sampling rearrangement strategy on OOD detection performance. It highlights a significant performance drop when this strategy is not used, indicating its importance for consistent optimization.

This figure shows the accuracy of the approximation used in the paper for the modified Bessel function of the first kind. The left panel plots the actual value of the approximation (log Îp(ε)) against the concentration parameter (ε) for different values of p (the order of the Bessel function). The right panel shows the difference (δ(ε)) between the approximation and the exact value obtained using the scipy library, illustrating the approximation error. The graphs demonstrate that the approximation becomes more accurate as p increases.

More on tables

This table presents the results of out-of-distribution (OOD) detection experiments using the CIFAR-10 dataset and a ResNet-18 model. It compares the performance of the proposed DRL method against various existing OOD detection methods. The metrics used are the False Positive Rate at 95% True Positive Rate (FPR95) and the Area Under the Receiver Operating Characteristic curve (AUROC). Lower FPR95 values and higher AUROC values indicate better performance. The table highlights the superior performance of DRL compared to other methods across different OOD datasets.

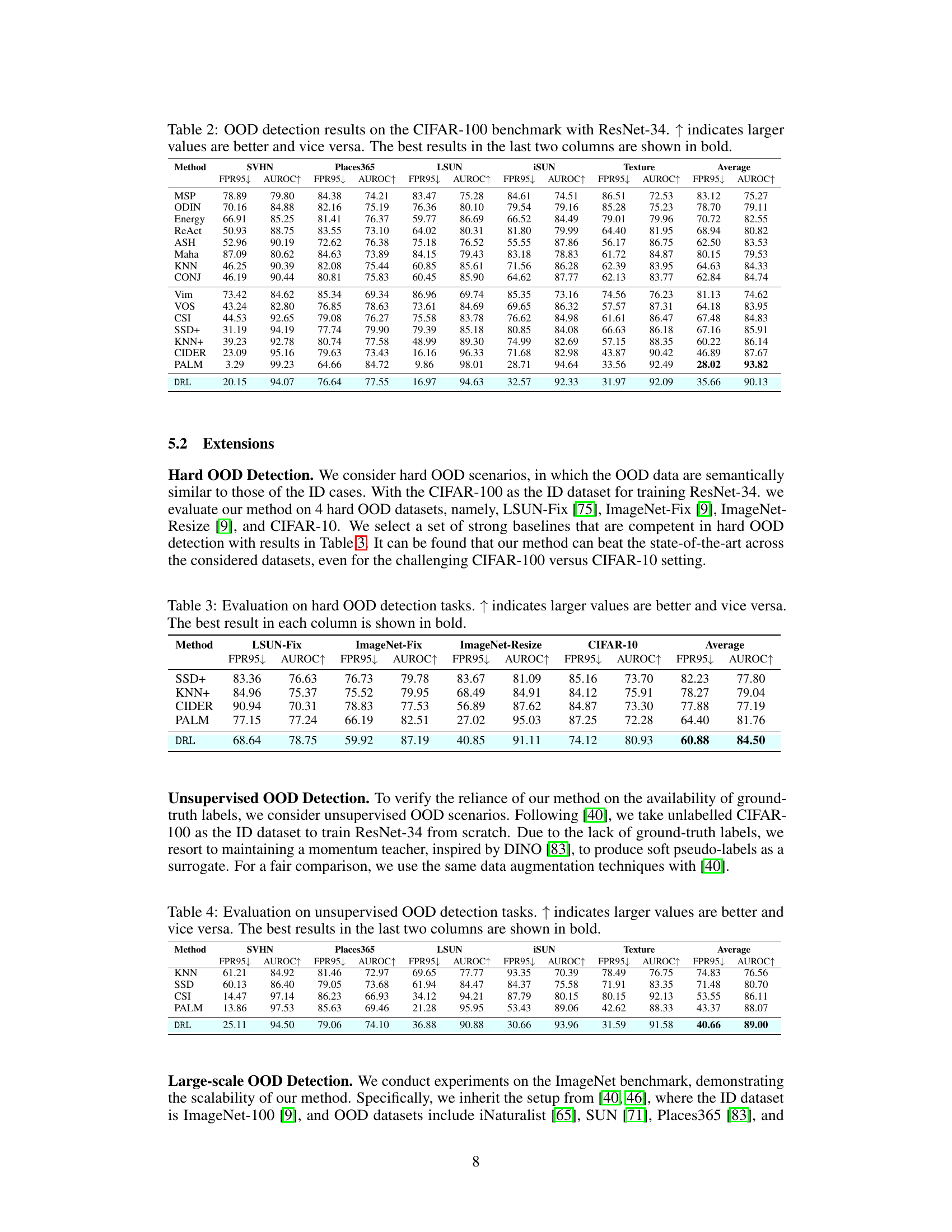
This table presents the results of hard out-of-distribution (OOD) detection experiments. Four challenging datasets (LSUN-Fix, ImageNet-Fix, ImageNet-Resize, and CIFAR-10) were used to evaluate the performance of several methods, including the proposed DRL approach. The performance is measured using two metrics: False Positive Rate at 95% true positive rate (FPR95) and Area Under the ROC curve (AUROC). Lower FPR95 and higher AUROC values are preferred. The table shows that DRL outperforms other methods on average.

This table presents the results of out-of-distribution (OOD) detection experiments using the CIFAR-10 dataset and a ResNet-18 model. It compares various OOD detection methods across multiple metrics (False Positive Rate at 95% true positive rate (FPR95) and Area Under the ROC Curve (AUROC)). Higher AUROC and lower FPR95 values indicate better performance. The table shows that the proposed DRL method significantly outperforms existing methods.

This table presents the results of an ablation study on the stability of the proposed method (DRL) for out-of-distribution (OOD) detection on the CIFAR-100 dataset. Five independent runs were conducted, and the mean and standard deviation of the FPR95 (False Positive Rate at 95% true positive rate) and AUROC (Area Under the Receiver Operating Characteristic curve) are reported for several OOD datasets (SVHN, Places365, LSUN, iSUN, Texture). This demonstrates the consistent performance of DRL across multiple runs.

Full paper

#