↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many imaging tasks involve solving linear inverse problems, where the goal is to reconstruct a clean image from noisy or incomplete measurements. A promising approach uses generative models, specifically those based on flow matching, as image priors to improve reconstruction quality. However, a major obstacle is the slow computation of log-likelihoods, which are crucial for efficient estimation. This is particularly problematic for high-dimensional images.
This paper introduces Iterative Corrupted Trajectory Matching (ICTM), a novel algorithm to efficiently solve these problems. ICTM cleverly approximates the MAP (Maximum A Posteriori) estimator by breaking down the complex objective function into smaller, more manageable local objectives. By leveraging Tweedie’s formula, ICTM efficiently performs gradient-based optimization steps, leading to computationally efficient and accurate reconstruction of images. Experiments on various linear inverse problems (super-resolution, deblurring, inpainting, compressed sensing) demonstrate that ICTM significantly outperforms existing flow-matching-based methods in terms of both speed and reconstruction quality.
Key Takeaways#
Why does it matter?#
This paper is important because it presents a novel and efficient algorithm for incorporating flow priors into linear inverse problems, a common challenge in various fields. It addresses computational bottlenecks associated with traditional methods using flow matching, opening up new possibilities for high-quality image reconstruction and improving efficiency of existing algorithms. This is highly relevant to current research trends in generative models and inverse problems, potentially impacting diverse fields like medical imaging and astronomy.
Visual Insights#

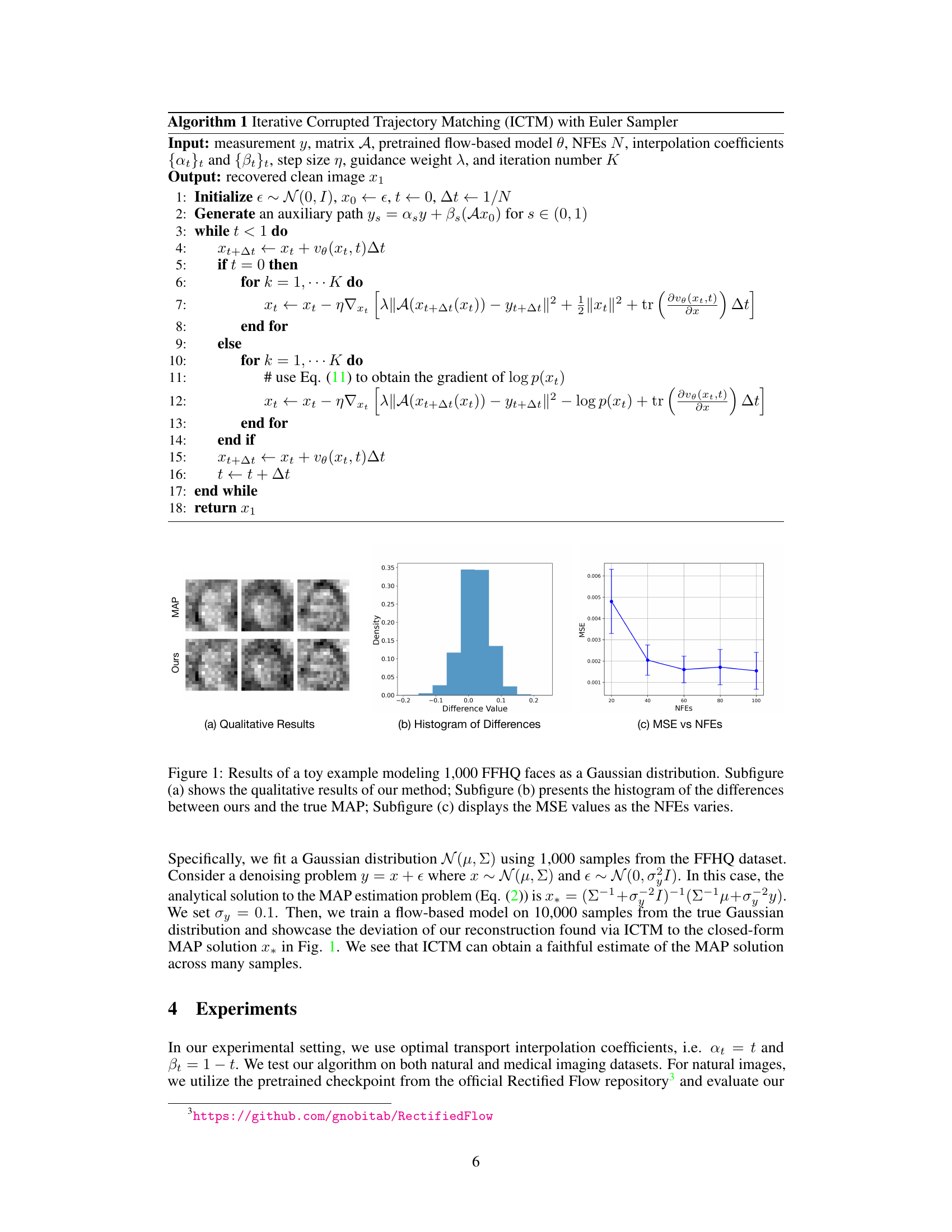
This figure shows the results of a toy experiment using 1000 FFHQ faces modeled as a Gaussian distribution. The experiment validates the ICTM algorithm by comparing its results to the known optimal MAP solution in a simplified denoising problem. Subfigure (a) provides qualitative results by visualizing the reconstructed images; (b) shows a histogram of the differences between ICTM’s solution and the true MAP solution, demonstrating the algorithm’s accuracy; and (c) plots the mean squared error (MSE) against the number of function evaluations (NFEs), showing the algorithm’s computational efficiency.
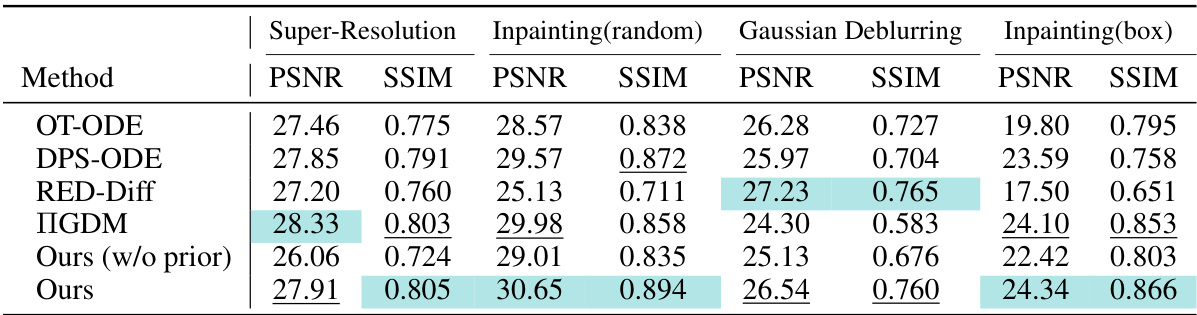
This table presents a quantitative comparison of different image reconstruction methods on the CelebA-HQ dataset for four tasks: super-resolution, inpainting (with random and box masks), and Gaussian deblurring. The methods are compared using Peak Signal-to-Noise Ratio (PSNR) and Structural Similarity Index (SSIM) metrics. The table highlights the best and second-best performing methods for each task, demonstrating the superior performance of the proposed ICTM algorithm.
In-depth insights#
Flow Matching Priors#
Flow matching priors offer a powerful approach to incorporating generative models into inverse problems. They leverage the efficiency of flow-based models, which directly estimate densities using a change-of-variables formula, avoiding the computationally expensive sampling required by diffusion models. The invertibility of flows provides direct access to likelihoods, facilitating MAP estimation. A key advantage lies in the ability to compute image likelihoods directly from the learned flow, making them suitable priors for various inverse problems like image deblurring and super-resolution. However, challenges remain in efficiently computing the log-likelihood, often requiring backpropagation through an ODE solver. This computational bottleneck is particularly problematic for high-dimensional problems. To address this, innovative techniques like Iterative Corrupted Trajectory Matching (ICTM) are developed to approximate MAP estimation efficiently, making flow matching priors a viable and increasingly attractive option for high-resolution image reconstruction.
Iterative ICTM#
The proposed Iterative Corrupted Trajectory Matching (ICTM) algorithm offers an efficient approach to solving linear inverse problems by leveraging flow-based generative models. Instead of directly optimizing the computationally expensive global MAP objective, ICTM cleverly approximates it through a sequence of simpler, local MAP objectives. This iterative refinement strategy, mathematically grounded in Tweedie’s formula and the concept of local posterior distributions, allows for significantly faster convergence. The algorithm sequentially refines intermediate trajectory points, ensuring both likelihood and prior consistency, ultimately leading to a high-quality reconstruction. The efficacy of ICTM is demonstrated across various inverse problems, including super-resolution, inpainting, and deblurring, showcasing its competitive performance against existing flow-matching based methods. However, limitations exist in the assumptions of exact trajectory compliance and the reliance on a straight-line interpolation, which are areas ripe for future improvement and generalization to more complex scenarios.
MAP Approximation#
The core idea revolves around efficiently approximating the Maximum A Posteriori (MAP) estimator for linear inverse problems. The paper cleverly tackles the computational bottleneck of directly calculating the log-likelihood from a flow-based generative model by introducing an iterative approach. Instead of computing the global MAP objective, which requires backpropagation through an ODE solver, it proposes a sequential optimization strategy targeting local MAP objectives. This decomposition simplifies the problem significantly, making it computationally feasible for high-dimensional image reconstruction. The mathematical justification employs Tweedie’s formula, showing that the sum of these local objectives converges to the global MAP estimate as the number of function evaluations increases. This iterative refinement, termed Iterative Corrupted Trajectory Matching (ICTM), provides a computationally efficient way to leverage flow-based priors for linear inverse problems such as super-resolution and deblurring, outperforming existing methods based on flow matching.
Empirical Validation#
An empirical validation section in a research paper is crucial for demonstrating the practical effectiveness of proposed methods. A strong empirical validation will involve a rigorous experimental design, selecting relevant datasets and metrics, employing proper comparison baselines, and presenting results clearly and comprehensively. The choice of datasets should be justified, reflecting the intended application domain and potential limitations. Appropriate evaluation metrics must align with the research question and provide quantitative assessments of performance. Meaningful comparisons against relevant state-of-the-art methods are crucial to showcasing advancements and highlighting the unique strengths of the novel approach. The overall clarity and organization of the empirical validation section significantly influence its impact, and it must be presented in a manner that is both accessible and informative for the reader, ultimately enhancing the credibility and significance of the research findings. Statistical analysis, including error bars and significance tests, is important in supporting claims about performance differences and ensuring reproducibility.
Future Directions#
Future research should address several key limitations. Generalizing the theoretical framework beyond optimal transport interpolation paths to accommodate diverse data distributions is crucial. Expanding the applicability of flow priors to nonlinear forward models is also essential for broader impact across various inverse problems. Addressing the current inability to quantify uncertainty in generated images and developing methods for post-processing to address this are vital for scientific applications. Exploring efficient techniques for handling high-dimensional problems, such as those encountered in medical imaging or remote sensing, is necessary to improve computational efficiency. Finally, investigation into more robust algorithms that are less sensitive to the choice of hyperparameters or initial conditions would enhance the overall reliability and applicability of flow-based methods for a wide range of inverse problems.
More visual insights#
More on figures

This figure shows a qualitative comparison of the image reconstruction results obtained using different methods on the CelebA-HQ dataset for four different tasks: super-resolution, inpainting (random mask), Gaussian deblurring, and inpainting (box mask). The results show that the method proposed in the paper generates reconstructions that align more closely with the ground truth images compared to other baselines, indicating better quality and higher detail preservation.

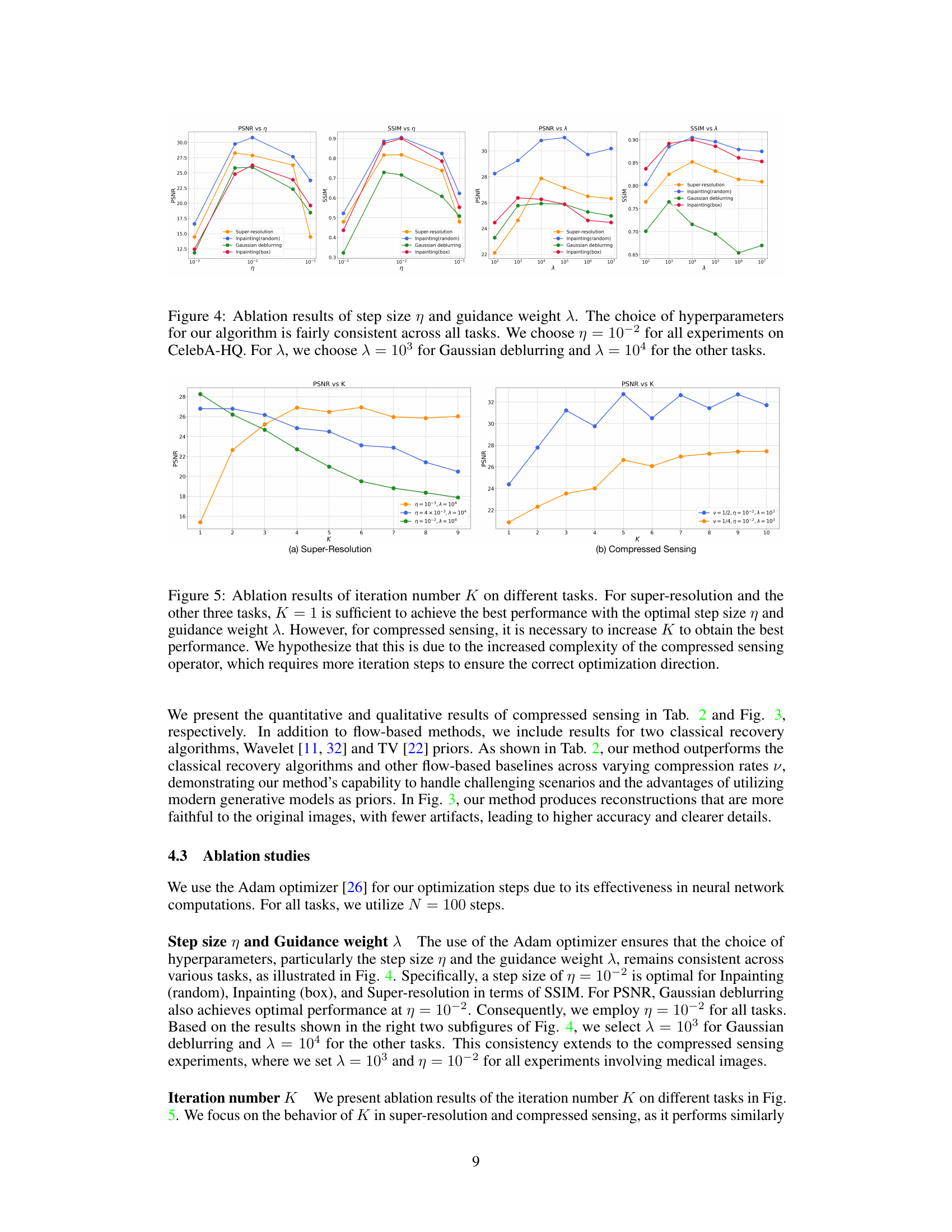
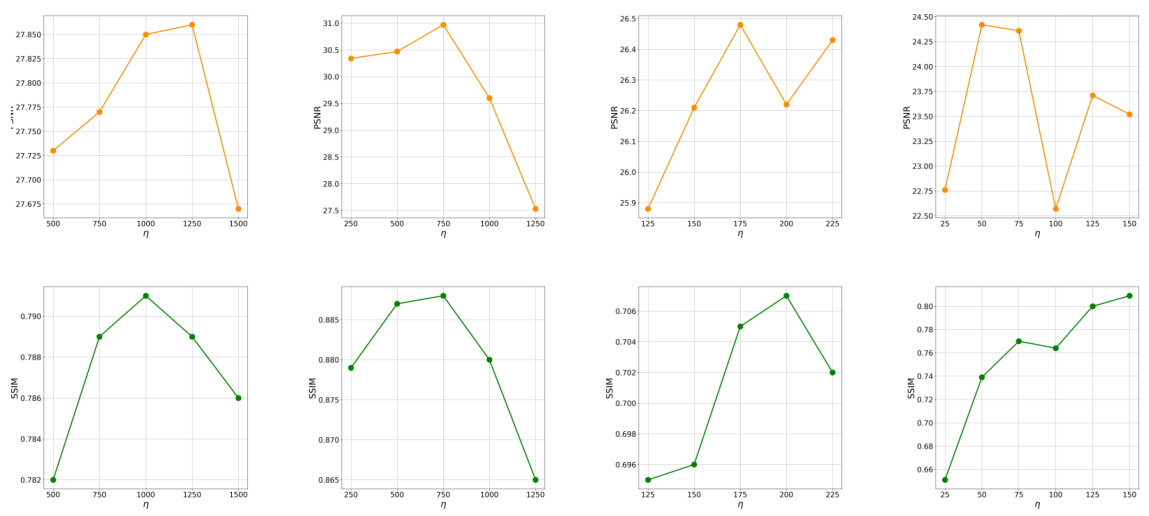
This figure shows the ablation study on the step size (η) and guidance weight (λ) hyperparameters of the ICTM algorithm. The results are presented for four different image reconstruction tasks: super-resolution, inpainting (random), Gaussian deblurring, and inpainting (box). The plots show the PSNR and SSIM values achieved for various values of η and λ. It demonstrates that the optimal hyperparameter settings for ICTM are relatively consistent across these different tasks, with η = 10⁻² working well for all tasks on the CelebA-HQ dataset and λ values set to 10³ for Gaussian deblurring and 10⁴ for the other tasks.

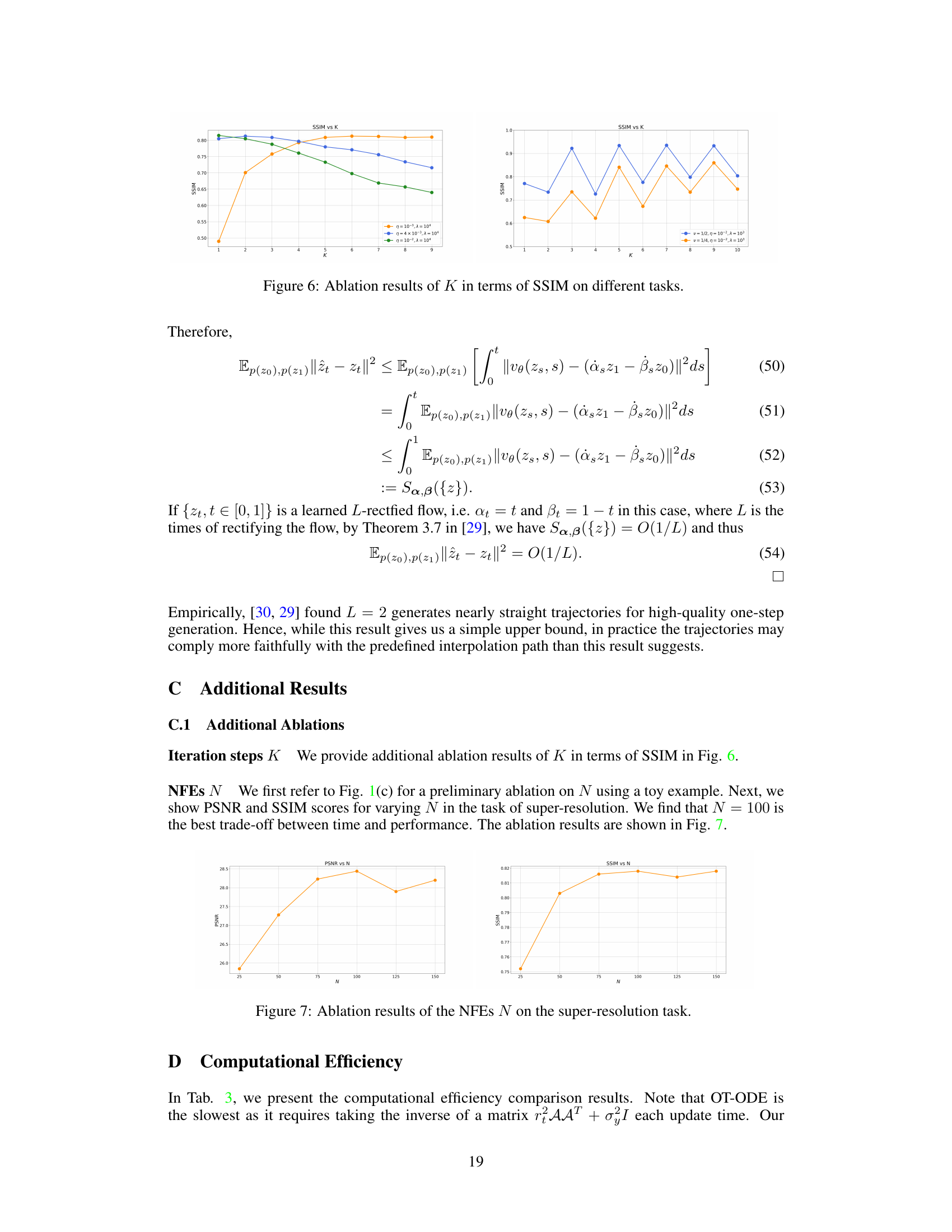
This figure shows the ablation study on the impact of the number of iterations (K) on the performance of ICTM across different image reconstruction tasks. It demonstrates that for super-resolution, inpainting, and deblurring, a single iteration (K=1) is optimal. However, for compressed sensing, more iterations are needed to achieve optimal performance, highlighting the increased complexity associated with this task.
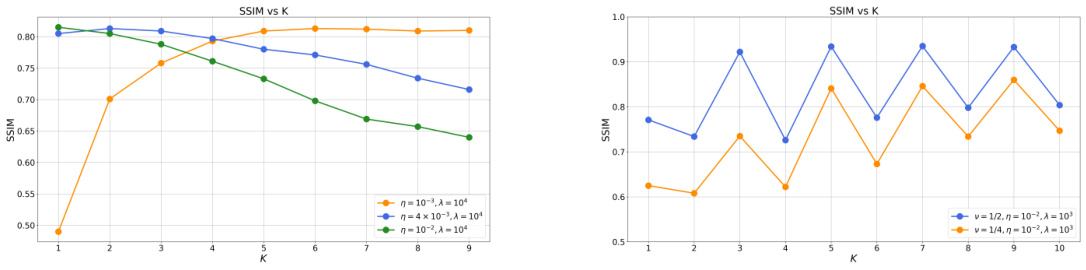
This figure shows the ablation study on the impact of the iteration number (K) on the performance of the ICTM algorithm across different inverse problems. While K=1 suffices for super-resolution, inpainting, and deblurring tasks, compressed sensing requires a larger K value for optimal performance. The authors hypothesize that the increased complexity of the compressed sensing operator necessitates more iterations to find the optimal solution.
This figure shows the results of a toy experiment to validate the proposed algorithm. The experiment uses a simplified denoising problem where the ground truth is known. The figure contains three subfigures: (a) Qualitative Results: Shows visual comparisons of reconstructions obtained via the proposed method with the ground truth. (b) Histogram of Differences: Shows a histogram of the differences between the reconstructions obtained via the proposed method and the ground truth. (c) MSE vs NFES: Shows a plot illustrating the mean squared error (MSE) of the reconstructions as a function of the number of function evaluations (NFEs).

This figure shows 200 samples generated from a flow-based generative model trained on 10,000 samples from a Gaussian distribution. These samples demonstrate the model’s ability to generate new images similar in style to the training data. The images are grayscale and appear to be face-like, although many are blurry or imperfect. This suggests the model has learned some aspects of face structure and variation from its training data but could benefit from further training or adjustments to its architecture.

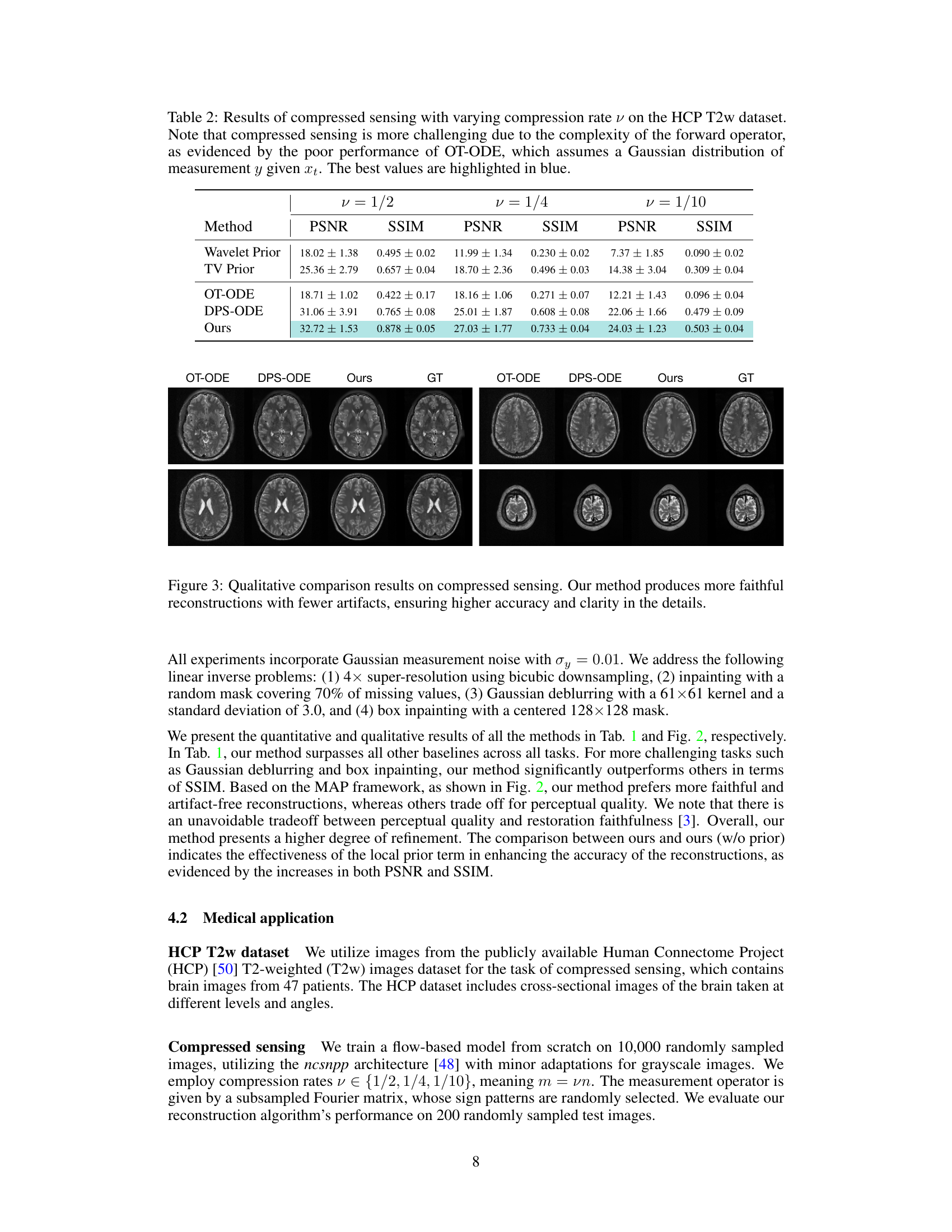
This figure shows a qualitative comparison of compressed sensing results using different methods. The left side shows the ground truth images, and the right side shows the reconstructed images generated by various methods, including the proposed ICTM method. Visual inspection reveals that ICTM produces images with fewer artifacts and higher clarity than the alternative methods, demonstrating its superior accuracy in compressed sensing tasks.

This figure shows the results of a toy experiment to validate the proposed ICTM algorithm. The experiment uses 1000 FFHQ faces modeled as a Gaussian distribution for a denoising task. It demonstrates the efficacy of ICTM in approximating the true Maximum A Posteriori (MAP) solution. Three subfigures are shown: (a) shows qualitative results comparing the reconstructed images to the ground truth, illustrating the visual fidelity of the algorithm. (b) is a histogram showing the distribution of differences between the results obtained by the algorithm and the true MAP solution, indicating the algorithm’s accuracy. (c) is a plot showing the Mean Squared Error (MSE) as a function of the number of function evaluations (NFEs), showcasing the computational efficiency of the ICTM approach.

This figure presents the results of a toy experiment where the authors approximate the Maximum a Posteriori (MAP) solution for a simplified denoising problem using a flow-based model and the proposed Iterative Corrupted Trajectory Matching (ICTM) algorithm. Subfigure (a) provides qualitative results by visually comparing reconstructions obtained using the ICTM algorithm with the ground truth. Subfigure (b) presents a histogram that visualizes the distribution of differences between the reconstructions obtained with the ICTM algorithm and the true MAP solution for the experiment, illustrating that the algorithm’s output is close to the optimal MAP solution. Lastly, subfigure (c) shows a plot of mean square error (MSE) against the number of function evaluations (NFEs), demonstrating the computational efficiency of the proposed algorithm.
This figure shows the ablation study on the number of function evaluations (NFEs) for the super-resolution task. It plots the PSNR and SSIM scores against different NFEs, allowing for a visual analysis of the trade-off between computational cost and performance in the super-resolution task. The results suggest an optimal NFE value that balances both aspects, indicating the efficiency and effectiveness of the proposed method.
More on tables
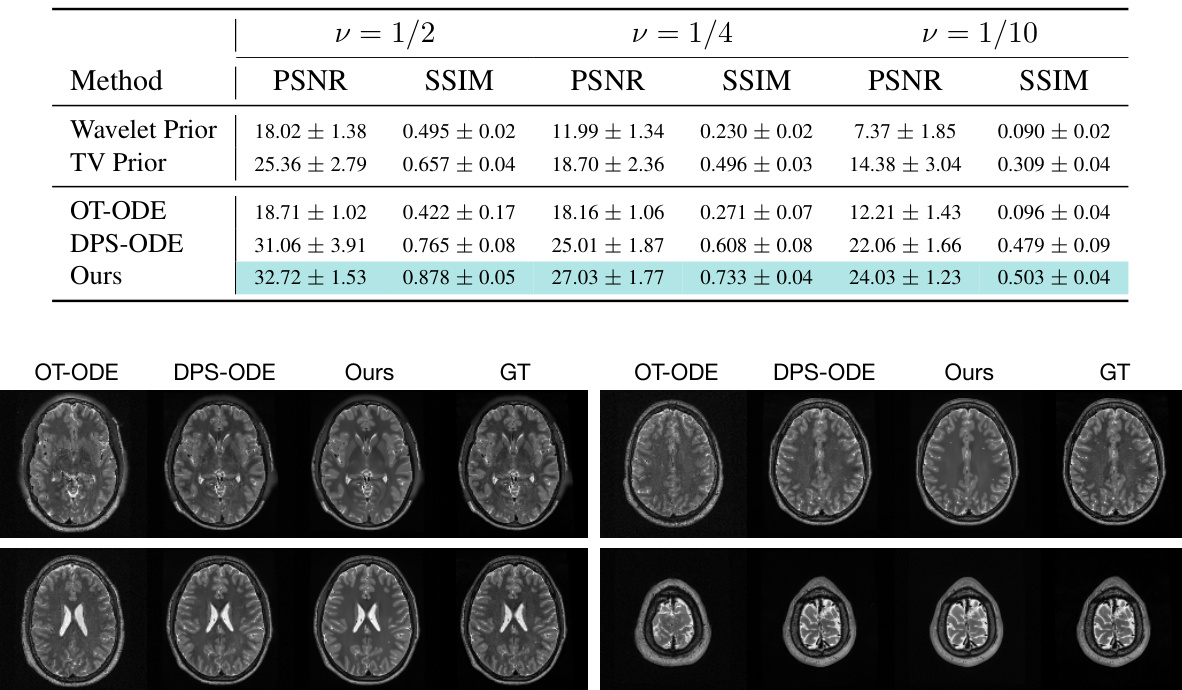
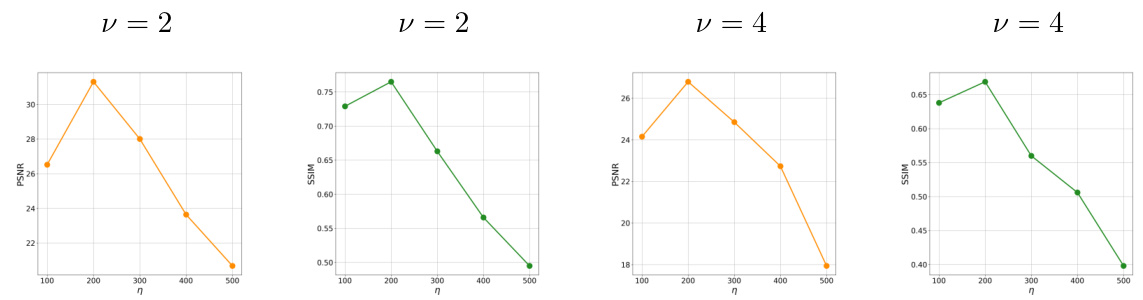
This table shows the quantitative results of compressed sensing experiments on the Human Connectome Project (HCP) T2w dataset using different compression rates (ν). The table compares the performance of the proposed ICTM method against several baselines (Wavelet Prior, TV Prior, OT-ODE, DPS-ODE) in terms of PSNR and SSIM. The results highlight the superior performance of ICTM, especially at higher compression rates, demonstrating its robustness in handling complex inverse problems.

This table presents a quantitative comparison of different image reconstruction methods on the CelebA-HQ dataset, focusing on peak signal-to-noise ratio (PSNR) and structural similarity index (SSIM). The results are organized by method and task (super-resolution, inpainting with random and box masks, and Gaussian deblurring). The table highlights the superior performance of the proposed ICTM algorithm compared to other baselines by showing the best PSNR and SSIM values in blue.
This table presents a quantitative comparison of different image reconstruction methods on the CelebA-HQ dataset. The methods are evaluated using Peak Signal-to-Noise Ratio (PSNR) and Structural Similarity Index (SSIM) metrics across four tasks: super-resolution, random inpainting, Gaussian deblurring, and box inpainting. The table highlights the best and second-best performing methods for each task, demonstrating the superior performance of the proposed method.
Full paper#