Does Egalitarian Fairness Lead to Instability? The Fairness Bounds in Stable Federated Learning Under Altruistic Behaviors

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it rigorously examines the often-overlooked relationship between egalitarian fairness and stability in federated learning (FL). It provides theoretically derived fairness bounds, which are essential for guiding the design and implementation of fair FL systems. The work also introduces a novel game-theoretic framework that considers clients’ altruistic behaviors, significantly enriching our understanding of FL dynamics. This opens up new avenues for research into stable and fair FL systems.

Visual Insights

#

This figure illustrates two different network structures among four clients in a federated learning setting. The left panel (Relation I) shows a fully connected network where each client is directly connected to all other clients. The right panel (Relation II) shows a partially connected network with fewer connections between clients. These different network topologies represent variations in the relationships between the clients, and this paper investigates how different client relationships and altruistic behaviors may affect stability in federated learning.

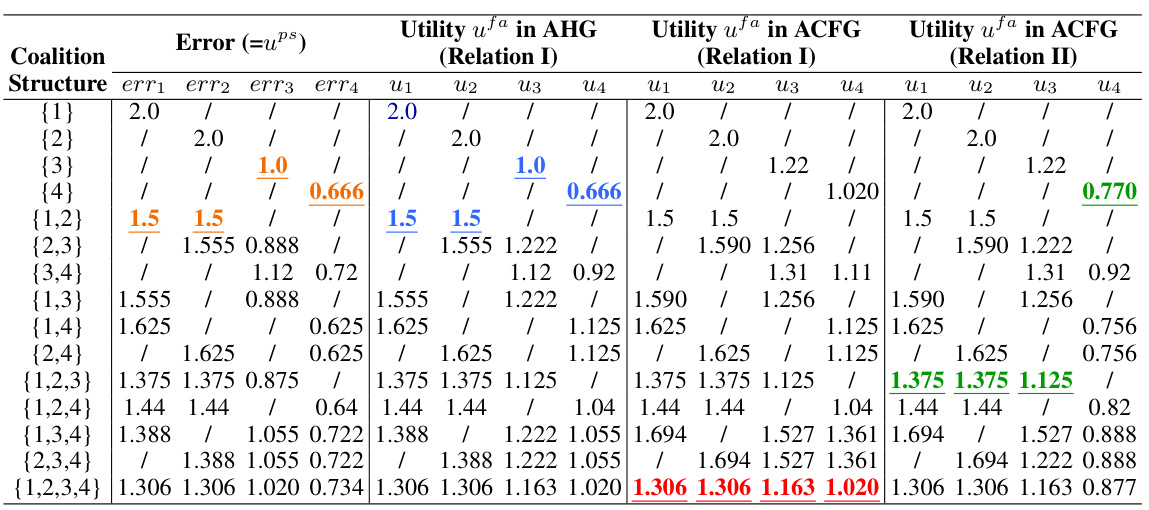
This table presents the error and utility values for four clients exhibiting friendly welfare altruistic behavior in two different network scenarios. It shows the results under both the Altruism Hedonic Game (AHG) and the Altruism Coalition Formation Game (ACFG) models for various coalition structures in fully connected and partially connected networks. This allows comparison of error and utility values for the same clients under different network configurations and game models.

In-depth insights

#

Fairness & Stability

#

The interplay between fairness and stability in federated learning (FL) is a critical concern. Egalitarian fairness, aiming for uniform model performance across all clients, can conflict with the inherent heterogeneity of client data. Data-rich clients, whose performance might decrease to achieve fairness, may be incentivized to leave the federation, thus undermining its stability. The paper investigates this tension, modeling FL as a game where clients’ altruistic behaviors and network relationships influence their decisions. The analysis reveals that egalitarian fairness doesn’t inherently cause instability. Instead, the optimal level of fairness achievable while maintaining core stability depends on client altruism and the structure of their interconnections. Theoretical bounds on achievable fairness are derived, clarifying the relationship between dataset size disparities, altruistic behavior, and system stability. These bounds provide guidelines for configuring FL systems that prioritize both fairness and long-term collaboration.

Altruism’s Role

#

Altruism, in the context of federated learning (FL), significantly impacts the stability and fairness of the system. The presence of altruistic clients, who prioritize the well-being of other clients in the coalition, can mitigate instability. This is because altruistic clients are less likely to abandon a coalition simply because of their own performance, even if it falls below their individual optimal. However, the type of altruism (purely altruistic vs. friendly altruistic) and the structure of the friendship network among clients also play critical roles. A fully connected network fosters greater altruism and thus stability, while a less connected network could still allow for instability even in the presence of altruism. The degree of altruism also impacts the achievable egalitarian fairness bounds, indicating a complex interplay between altruistic behavior, network topology, and fairness. Understanding this interplay is vital for designing stable and fair FL systems. Therefore, incorporating models of altruistic behavior into FL is essential for accurately predicting the system’s dynamics and devising effective strategies to achieve both stability and fairness.

Optimal Bounds

#

The concept of ‘Optimal Bounds’ in a research paper likely refers to the limits or constraints within which a system or process can operate while maintaining specific desirable properties. In the context of a fairness-focused machine learning model, these bounds define the maximum level of fairness achievable without compromising other crucial aspects, such as the stability of the system or the overall model performance. Determining these optimal bounds involves a rigorous analysis considering various factors like data distribution, client behavior, and network topology. The results would be expressed as mathematical formulas or inequalities, providing concrete guidance to researchers and practitioners on how much fairness can be realistically implemented in a given setting. The significance lies in balancing fairness with practical considerations to create a sustainable and functional system. The discovery of such optimal bounds is a significant theoretical contribution, offering a practical framework for designing fair machine learning models.

Game-Theoretic Model

#

A game-theoretic model in the context of federated learning (FL) offers a powerful framework for analyzing the strategic interactions between participating clients. It moves beyond simplistic assumptions of client homogeneity and pure self-interest, incorporating factors like altruism and friendship networks. This nuanced approach allows researchers to model how clients might behave given their individual data, the performance of the global model, and the well-being of their collaborators. By modeling FL as a coalition formation game, researchers can predict the stability of the system, which is crucial for successful collaboration. Analyzing the relationships between the level of altruism, network topology, and the fairness of the model’s performance becomes paramount. This framework provides a crucial tool for understanding and designing mechanisms to incentivize client participation and improve the overall efficiency and fairness of federated learning systems. The optimal egalitarian fairness bounds, derived through the game-theoretic model, provide practical guidance to system designers, ensuring both stability and desirable levels of fairness across all participants.

Future Research

#

Future research directions stemming from this work could explore more complex task scenarios beyond mean estimation, examining how different fairness notions (like proportional fairness) impact stability. The impact of various human behaviors (reciprocity, bounded rationality) on stability in fair FL also warrants investigation. Further, rigorous theoretical analysis could expand to encompass more complex model settings (e.g., overfitting), to develop robust fairness bounds in real-world scenarios. Additionally, it would be valuable to design incentive mechanisms that encourage client participation and maintain coalition stability, particularly under high fairness requirements. Finally, extensive empirical validation using more diverse datasets, heterogeneous client behavior, and different model architectures would strengthen the study’s applicability.

More visual insights

#

More on figures

This figure displays the results of experiments conducted on a fully connected friend-relationship network, comparing theoretically derived fairness bounds with the empirically observed fairness in the core-stable grand coalition. It shows how these bounds align with the empirically achieved fairness under different client behaviors: purely selfish, purely welfare altruistic, purely equal altruistic, friendly welfare altruistic, and friendly equal altruistic. The x-axis represents the coefficient p (introduced to increase the aggregation weight of clients with higher local errors), and the y-axis represents the fairness bound (λ). The green dashed line represents the theoretical bound, and the red solid line represents the empirically achieved fairness within the core-stable grand coalition.

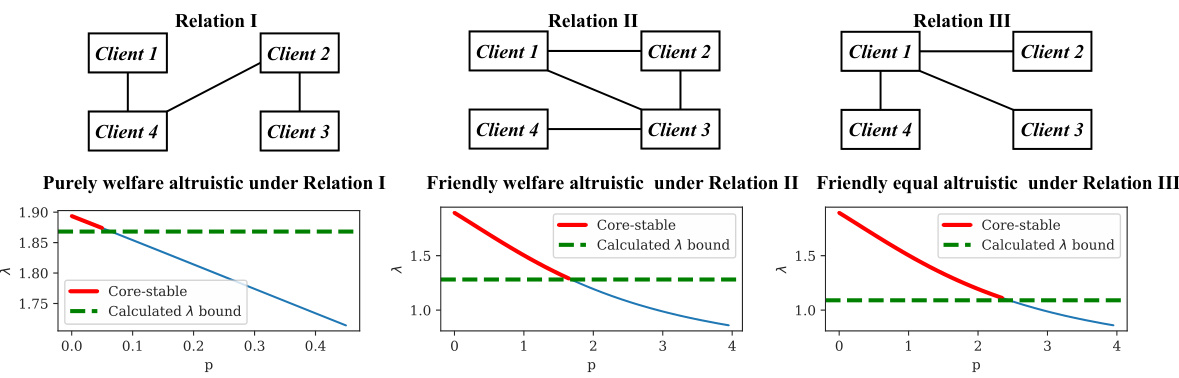
This figure displays the results of experiments conducted on partially connected friend-relationship networks. It shows the alignment between theoretically derived egalitarian fairness bounds (green dashed lines) and empirically observed fairness within core-stable grand coalitions (red solid lines). This alignment is demonstrated across various client behaviors: purely welfare altruistic, friendly welfare altruistic, and friendly equal altruistic. The x-axis represents the selfishness degree parameter (p), and the y-axis represents the fairness (λ).

This figure displays the results of experiments conducted using a fully connected friends-relationship network. It shows the relationship between the theoretically derived egalitarian fairness bounds and the empirically achieved egalitarian fairness within a core-stable grand coalition, across various client behaviors (purely selfish, purely welfare altruistic, purely equal altruistic, friendly welfare altruistic, and friendly equal altruistic). The x-axis represents the fairness coefficient (p), and the y-axis represents the egalitarian fairness (λ). The green dashed line represents the theoretical bound, and the red solid line represents the empirically observed fairness in the core-stable grand coalition. The figure demonstrates the strong alignment between theoretical predictions and experimental results, validating the theoretical fairness bounds.

This figure shows the comparison between theoretical and empirical results of egalitarian fairness bounds in a fully connected friend-relationship network under different client behaviors (purely selfish, purely welfare altruistic, purely equal altruistic, friendly welfare altruistic, friendly equal altruistic). The green dashed line represents the theoretical bound, and the red solid line represents the empirically achieved egalitarian fairness within the core-stable grand coalition. The x-axis represents the parameter p, which controls the aggregation weight of clients with higher local errors, and the y-axis represents the fairness bound (λ).

Full paper

#