↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
The reproducibility crisis in AI and other sciences necessitates a formal framework to analyze algorithmic replicability. This paper investigates the computational aspects of replicability, exploring its connections to various learning paradigms, including online learning, statistical queries (SQ), and differential privacy. Existing research has primarily focused on statistical connections, overlooking crucial computational aspects. This paper tackles this gap.
The research uses concept classes to design efficient replicable learners. It presents a novel replicable lifting framework inspired by prior work that translates efficient replicable learners under uniform marginal distribution to those under any marginal distribution, thus enhancing our understanding of replicability’s computational landscape. The study reveals a computational separation between efficient replicability and online learning, highlighting the distinct nature of these two properties. Additionally, it demonstrates a transformation from pure differential privacy learners to replicable learners. These findings significantly advance our understanding of computational stability.
Key Takeaways#
Why does it matter?#
This paper is crucial because it bridges the gap between statistical and computational aspects of replicability, a vital concept in ensuring reliable AI. It offers new algorithms and computational tools, pushing the boundaries of what’s possible in areas like online learning, statistical queries, and differential privacy, thus shaping future research directions.
Visual Insights#
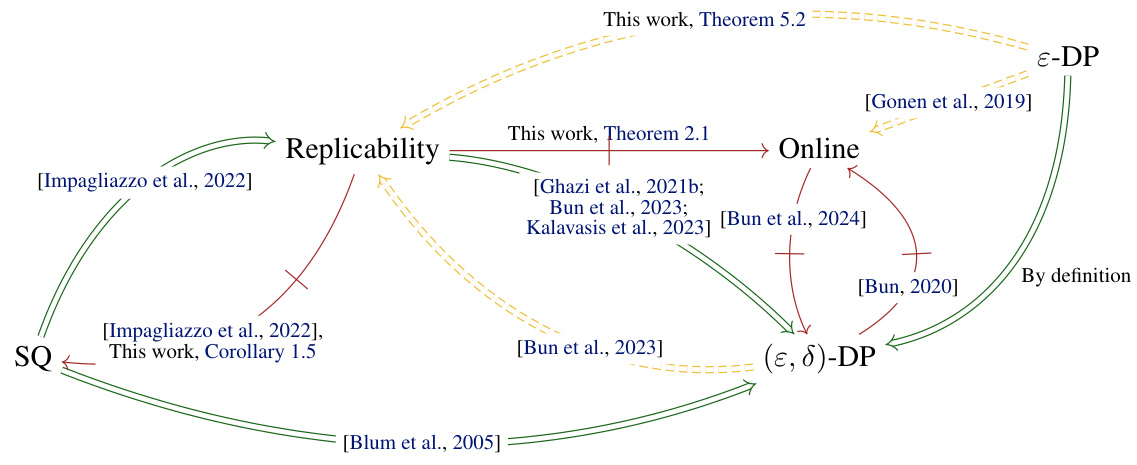
This figure summarizes the computational relationships between several learning paradigms and notions of algorithmic stability, including replicability, online learning, differential privacy, and statistical queries. Arrows indicate whether efficient transformations exist between these learning settings, with different arrow types indicating different transformation properties (black-box, conditional, or separation).

This figure summarizes the computational relationships between several learning paradigms including replicability, approximate differential privacy, pure differential privacy, online learning, and Statistical Queries (SQ). The arrows show whether an efficient transformation exists between paradigms (green double arrow for efficient black-box transformation, orange dashed double arrow for efficient transformation under additional assumptions, red slashed arrow for computational separation).
Full paper#



















