↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Constrained Markov Decision Processes (CMDPs) are widely used in reinforcement learning to model problems where agents must optimize rewards while satisfying constraints. However, solving CMDPs, especially those with many parameters, is computationally expensive, requiring many data samples. Existing algorithms have high sample complexity, making them inefficient for complex problems.
This paper introduces the Primal-Dual Accelerated Natural Policy Gradient (PD-ANPG) algorithm. PD-ANPG leverages momentum-based acceleration to significantly reduce the sample complexity, achieving the theoretical lower bound for general parameterized policies. The new algorithm outperforms existing methods, making it highly efficient for solving complex CMDPs.
Key Takeaways#
Why does it matter?#
This paper is crucial because it significantly improves the sample complexity for solving constrained Markov Decision Problems (CMDPs), a common challenge in reinforcement learning. This advancement allows for more efficient learning, especially with complex, high-dimensional problems, opening new avenues for applications in various fields.
Visual Insights#
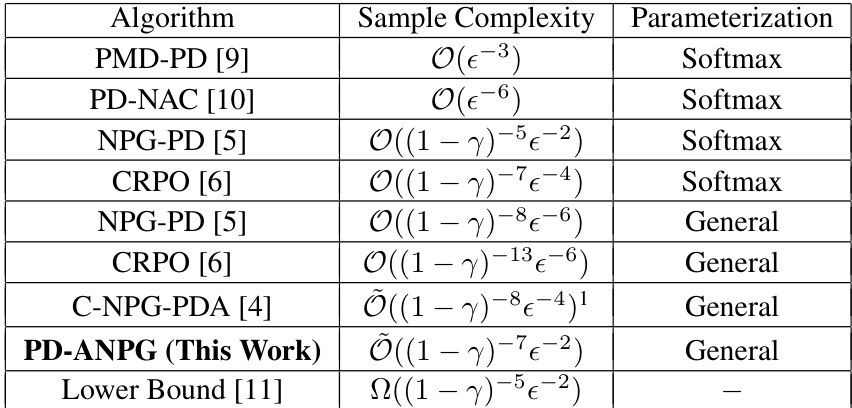
The table summarizes the sample complexity of various algorithms for solving constrained Markov Decision Processes (CMDPs) with different policy parameterizations. It shows the sample complexity (a measure of the number of samples needed to find a near-optimal solution) for both softmax and general parameterizations, along with the theoretical lower bound. The discount factor (γ) is also considered, reflecting its influence on sample complexity. The table highlights the improvement achieved by the proposed PD-ANPG algorithm.
Full paper#



















