↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Knowledge distillation (KD) aims to transfer knowledge from a large teacher model to a smaller student model. Traditionally, Kullback-Leibler divergence (KL-Div) has been the dominant method for measuring the difference between teacher and student predictions. However, KL-Div has limitations, particularly in handling complex relationships between different categories and non-overlapping distributions which can occur in intermediate layers of neural networks. These limitations hinder effective knowledge transfer and limit the performance of the student model.
This paper introduces Wasserstein Distance (WD) as a new metric for KD, addressing the shortcomings of KL-Div. The authors propose two methods: WKD-L for logit distillation (using discrete WD) and WKD-F for feature distillation (using continuous WD). Their experiments across image classification and object detection show that WKD significantly outperforms existing KL-Div based methods, showcasing WD’s effectiveness in knowledge transfer. This highlights the potential of WD as a superior metric for KD, potentially revolutionizing model compression and transfer learning techniques.
Key Takeaways#
Why does it matter?#
This paper is crucial because it challenges the dominance of KL-divergence in knowledge distillation, a widely used technique in deep learning. By introducing Wasserstein distance, it offers a novel approach that addresses the limitations of KL-divergence, particularly when handling non-overlapping distributions and complex relationships among categories. This opens new avenues for improving the efficiency and effectiveness of knowledge transfer in various deep learning tasks, impacting model compression and transfer learning. The extensive experimental results showcasing the superiority of the proposed method further strengthen its significance.
Visual Insights#

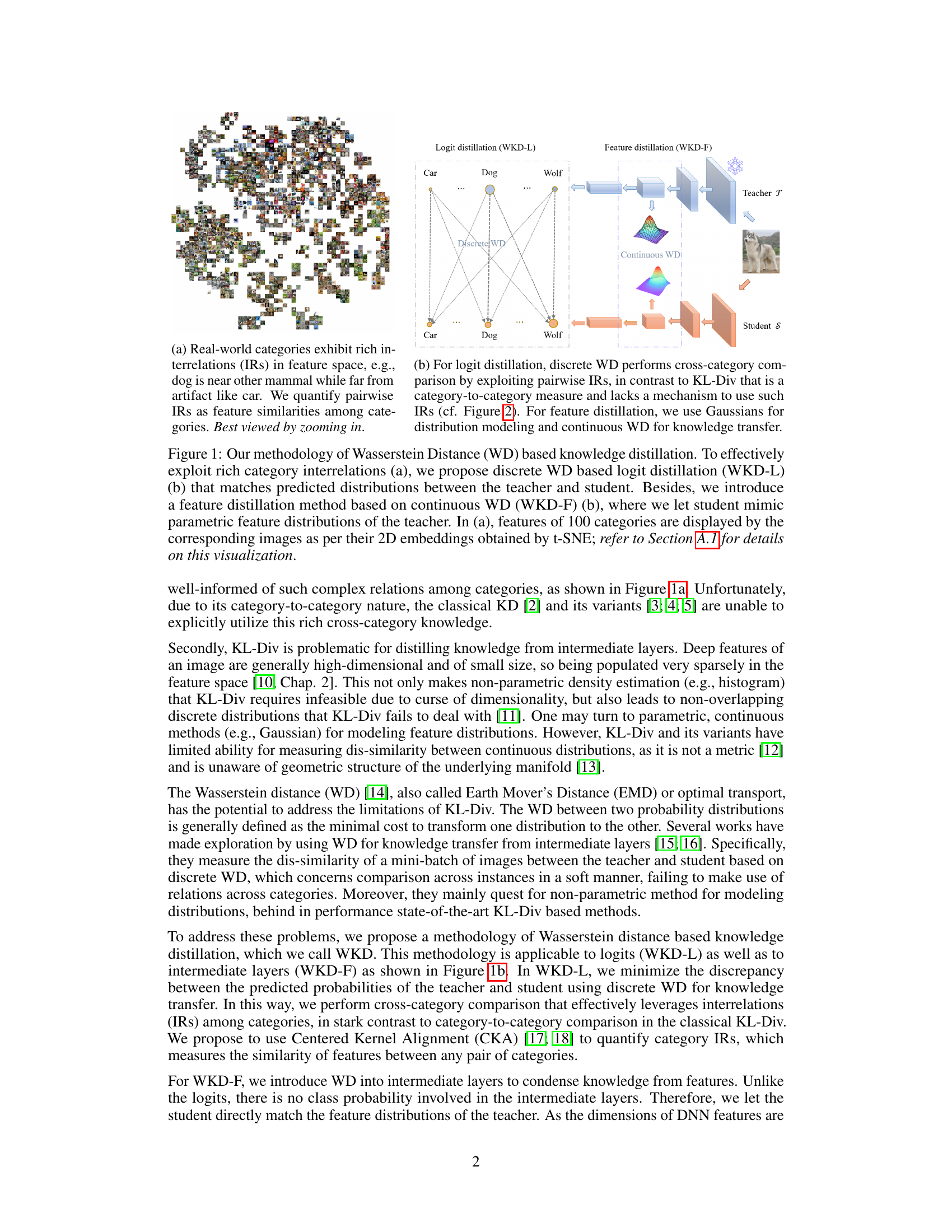
This figure illustrates the proposed Wasserstein Distance (WD)-based knowledge distillation method. It shows how the method leverages rich category interrelations. The left panel (a) visualizes real-world category interrelations in feature space using t-SNE on 100 categories. The right panel (b) illustrates the proposed methods: WKD-L (discrete WD for logit distillation) and WKD-F (continuous WD for feature distillation). WKD-L focuses on cross-category comparison of probabilities, while WKD-F uses continuous WD to transfer knowledge from intermediate layers by modeling feature distributions with Gaussians.
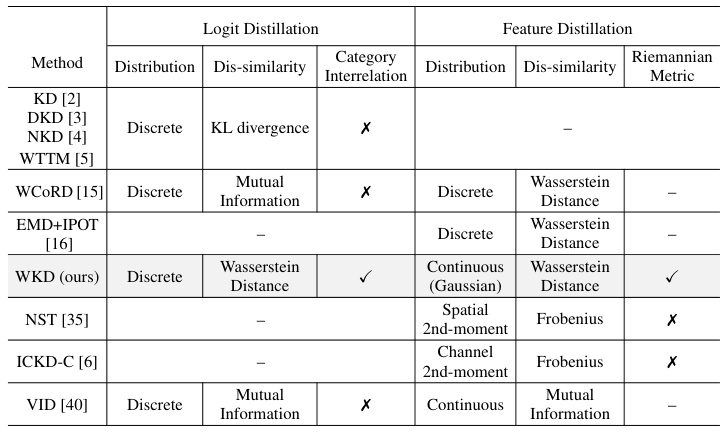
This table compares the proposed Wasserstein Distance-based Knowledge Distillation (WKD) method with other related knowledge distillation methods. The comparison highlights key differences in terms of the type of distribution used (discrete vs. continuous), the dissimilarity measure employed (KL divergence, Mutual Information, or Wasserstein Distance), whether cross-category interrelations are considered, and whether the method utilizes the Riemannian metric of Gaussian distributions. The table provides a concise overview of the strengths and weaknesses of different KD approaches.
In-depth insights#
WD vs. KL-Div#
The core of this paper lies in comparing and contrasting Wasserstein Distance (WD) and Kullback-Leibler Divergence (KL-Div) for knowledge distillation. KL-Div, the traditional method, suffers from limitations in handling non-overlapping distributions and a lack of cross-category comparison. It primarily focuses on the probability distributions of individual categories, neglecting the relationships between them. The authors propose WD as a superior alternative, arguing that it effectively addresses these shortcomings. WD considers the geometry of the underlying feature space, enabling cross-category comparisons and robust handling of non-overlapping distributions. This is particularly beneficial when applied to intermediate layers of deep neural networks. The experimental results demonstrate that WD-based knowledge distillation significantly outperforms KL-Div-based methods in various image classification and object detection tasks. The superior performance highlights WD’s ability to leverage rich category interrelations and its suitability for feature distribution matching.
WKD Methodologies#
The Wasserstein Distance Knowledge Distillation (WKD) methodologies presented offer a compelling alternative to traditional Kullback-Leibler (KL) divergence-based approaches. WKD directly addresses KL’s limitations in handling non-overlapping distributions and its inability to capture cross-category relationships among classes. The use of discrete WD for logit distillation (WKD-L) allows for a more nuanced comparison of probability distributions, explicitly leveraging inter-category similarities. This contrasts sharply with KL-divergence, which only considers category-wise probabilities. Furthermore, the introduction of continuous WD for feature distillation (WKD-F), employing parametric Gaussian modeling, enables effective knowledge transfer from intermediate layers where non-parametric methods struggle. WKD-F’s continuous approach leverages the underlying manifold geometry, providing a more robust and accurate measure of dissimilarity compared to KL-divergence’s limitations in high-dimensional spaces. The combined logit and feature distillation methodologies of WKD demonstrate a holistic approach to knowledge transfer, potentially enhancing model performance beyond what’s achievable using KL-based methods alone.
Empirical Gains#
An ‘Empirical Gains’ section in a research paper would detail the practical improvements achieved by the proposed method. It would go beyond theoretical analysis to demonstrate real-world effectiveness. This might involve comparing performance metrics (e.g., accuracy, F1-score, mAP) on standard benchmark datasets against state-of-the-art methods. Key aspects to highlight include the magnitude of improvement, presenting results with statistical significance (e.g., confidence intervals, p-values). The discussion should also address whether gains are consistent across different datasets or model variations, and if there are specific conditions where improvements are more pronounced. Furthermore, a nuanced discussion of computational costs associated with achieving these gains is vital, weighing trade-offs between enhanced performance and increased resource demands. Finally, it should clearly state whether the empirical results confirm the theoretical predictions, revealing any unexpected findings or limitations.
WKD Limitations#
The Wasserstein Distance-based Knowledge Distillation (WKD) method, while demonstrating strong performance improvements over traditional KL-divergence approaches, presents certain limitations. Computational cost is a major factor; discrete WKD-L, while leveraging rich category interrelations, involves solving an entropy-regularized linear program, significantly increasing the computational complexity. The use of Gaussian distributions for continuous WKD-F simplifies calculations but might not perfectly model the underlying distribution of deep features. Generalizability also needs consideration; the performance improvements might vary across different model architectures, datasets, and hyper-parameter settings. The reliance on techniques like CKA for quantifying category interrelations introduces further assumptions and potential sources of error that may limit the method’s broad applicability. Lastly, the method’s effectiveness hinges on the availability and quality of teacher models. The need for pre-trained, high-performing teacher models could be a barrier, especially in resource-constrained scenarios. Therefore, future research should focus on algorithmic efficiency improvements, exploring alternative distribution modeling techniques, and addressing the generalizability and scalability challenges for wider adoption.
Future of WKD#
The future of Wasserstein Distance-based Knowledge Distillation (WKD) is promising, given its demonstrated advantages over traditional KL-divergence methods. Further research should focus on addressing the computational cost of discrete WD in WKD-L, perhaps through exploration of more efficient optimization algorithms or approximations. Developing more robust and efficient methods for estimating feature distributions in WKD-F, especially for high-dimensional data, is crucial. This might involve investigating alternative parametric distributions beyond Gaussians or exploring non-parametric approaches that effectively handle the curse of dimensionality. Exploring the application of WKD to various modalities beyond images (e.g., text, audio, time series) could significantly broaden its impact. Finally, investigating the theoretical properties and limitations of WKD more rigorously is necessary to fully understand its capabilities and potential pitfalls, thereby enhancing its reliability and trustworthiness.
More visual insights#
More on figures
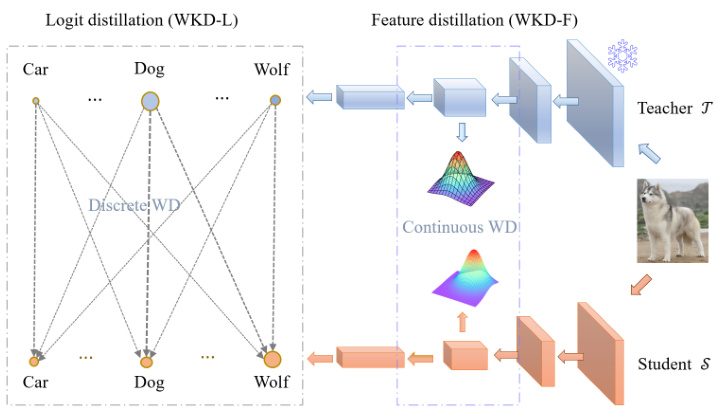
This figure illustrates the proposed Wasserstein Distance (WD)-based knowledge distillation methods. Panel (a) shows how real-world categories have complex interrelationships in feature space. Panel (b) details the two proposed methods: WKD-L (logit distillation) uses discrete WD to compare probability distributions across categories, while WKD-F (feature distillation) leverages continuous WD to model and match the feature distributions of the teacher and student in intermediate layers.
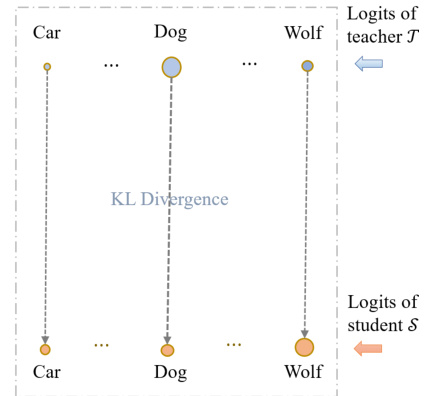
This figure illustrates the limitations of Kullback-Leibler Divergence (KL-Div) in knowledge distillation. KL-Div only compares the probabilities of corresponding categories between the teacher and student models, lacking a mechanism for cross-category comparison. The figure shows this limitation visually. It contrasts KL-Div’s category-to-category comparison (vertical lines between corresponding categories) with the cross-category comparisons enabled by Wasserstein Distance (WD), shown in Figure 1b in the paper. The figure highlights that KL-Div is a category-to-category measure, lacking a way to effectively use rich interrelations (IRs) among categories, unlike WD.
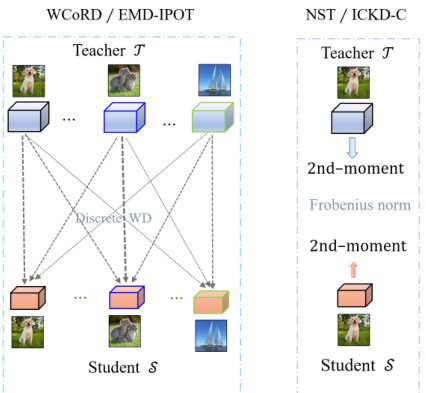
This figure compares two different approaches to knowledge distillation using Wasserstein distance. WCORD/EMD-IPOT uses discrete Wasserstein distance to match the distributions of features across instances between teacher and student models. In contrast, NST/ICKD-C uses the Frobenius norm of 2nd-moments of features for distillation, comparing distributions at an instance level. Both methods aim to transfer knowledge from intermediate layers of a deep neural network.

This figure illustrates the proposed Wasserstein Distance-based knowledge distillation method (WKD). It highlights two key aspects: logit distillation (WKD-L) and feature distillation (WKD-F). WKD-L leverages discrete WD to compare probability distributions across categories, considering relationships between categories. WKD-F uses continuous WD with Gaussian distribution modeling to transfer knowledge from intermediate layers. The visualization in (a) uses t-SNE to show the relationships between categories in feature space. (b) presents schematic diagrams of the methods.

This figure illustrates the proposed Wasserstein Distance (WD)-based knowledge distillation methodology. It shows how the method leverages rich interrelations between categories for both logit distillation (WKD-L) and feature distillation (WKD-F). WKD-L uses discrete WD to compare probability distributions across categories, unlike KL-divergence which only compares corresponding categories. WKD-F uses continuous WD with parametric Gaussian modeling of feature distributions at intermediate layers. The visualization in (a) uses t-SNE to display 2D embeddings of features from 100 categories represented by their corresponding images, showcasing the rich inter-category relationships. Part (b) shows the overall architecture of the proposed distillation methods.
This figure illustrates the proposed Wasserstein Distance (WD)-based knowledge distillation method. It shows how the method leverages rich category interrelations for logit distillation (WKD-L) using discrete WD and for feature distillation (WKD-F) using continuous WD. The figure also visualizes real-world category interrelations in feature space using t-SNE.
This figure illustrates the proposed Wasserstein Distance (WD)-based knowledge distillation methodology. It shows how the method leverages rich category interrelations (IRs) in a feature space. The figure highlights two key approaches: WKD-L (logit distillation) which performs cross-category comparison using discrete WD and WKD-F (feature distillation) that uses continuous WD to transfer knowledge from intermediate layers. It also includes a visualization of real-world category interrelations (IRs) which are used for a more accurate comparison.

This figure visualizes the differences between teacher and student models using two methods: WKD-L (logit distillation) and WKD-F (feature distillation). Panel (a) shows heatmaps representing the discrepancies in the correlation matrices of logits between the teacher and student models for two network settings (ResNet32x4 to ResNet8x4 and VGG13 to VGG8). Lighter colors indicate higher similarity between the teacher and student, suggesting better knowledge transfer with WKD-L. Panel (b) shows heatmaps illustrating discrepancies in feature distributions using the WD metric for the same network settings. Again, lighter colors suggest more similar distributions and better knowledge transfer with WKD-F. The visualization demonstrates that WKD-L and WKD-F achieve more similar results to the teacher models compared to standard methods.

This figure visualizes the differences in correlation matrices between student and teacher logits (a) and feature distributions between student and teacher (b) for different model architectures. In part (a), lighter colors in WKD-L compared to KD indicate that WKD-L produces correlation matrices more similar to the teacher. Part (b) shows that WKD-F demonstrates smaller discrepancies with the teacher than FitNet, suggesting it better mimics the teacher’s distributions.
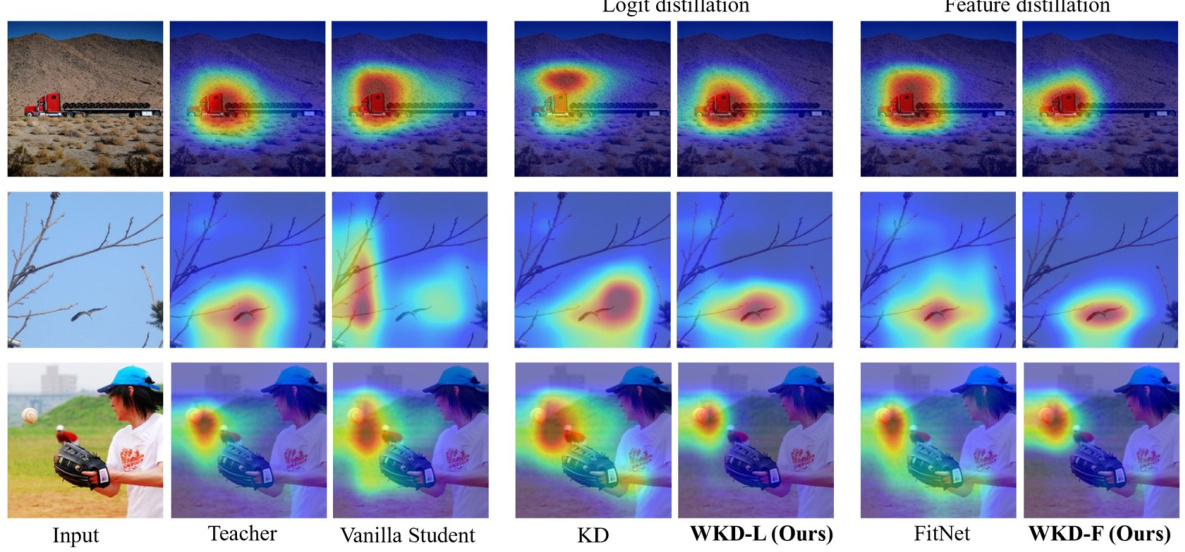
This figure visualizes class activation maps (CAMs) for three example images using Grad-CAM. It compares the CAMs generated by the teacher model, a vanilla student model (trained without distillation), a student model trained with the standard KL-divergence based KD method, a student model trained with the proposed WKD-L (logit distillation), a student model trained with the FitNet feature distillation method, and finally a student model trained with the proposed WKD-F (feature distillation) method. The purpose is to show how well each distillation method is able to transfer knowledge from the teacher, as evidenced by how similar the CAMs of the student models are to the CAMs of the teacher model.
More on tables
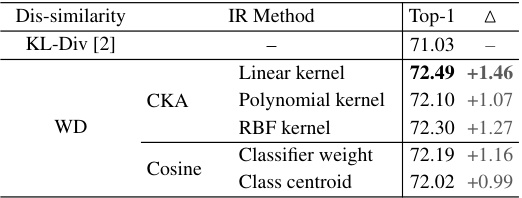
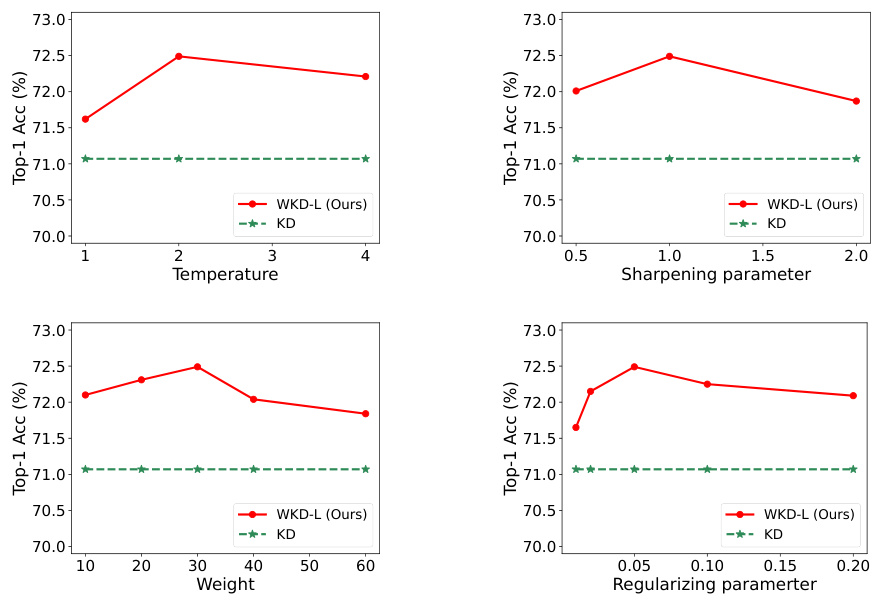
This table presents an ablation study on the proposed WKD-L method for image classification on the ImageNet dataset. It compares the performance of WKD-L against the baseline KL-Div method and its variants, and analyzes the impact of different methods for modeling category interrelations (IRs). The results show that WKD-L consistently outperforms KL-Div, and the choice of IR modeling method significantly affects the performance of WKD-L.
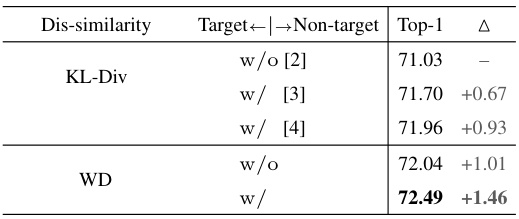
This table presents an ablation study for the WKD-L (Wasserstein Distance based Knowledge Distillation for Logits) method on the ImageNet dataset. It compares the performance of WKD-L against KL-Div (Kullback-Leibler Divergence) based methods with and without target-non-target probability separation, showing the improvement achieved by WKD-L. Different interrelation (IR) modeling methods using CKA (Centered Kernel Alignment) with various kernels (Linear, Polynomial, RBF) and cosine similarity with different category prototypes (classifier weights, class centroids) are also compared.
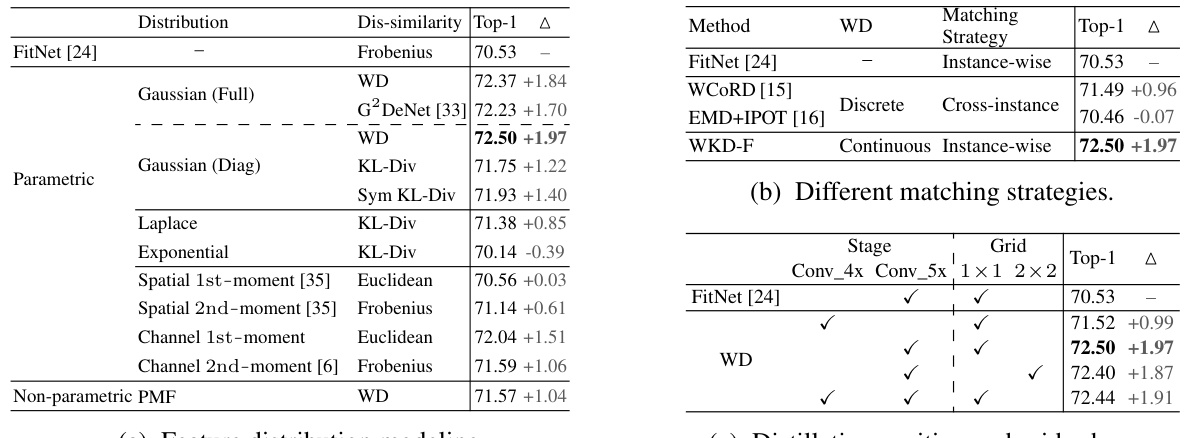
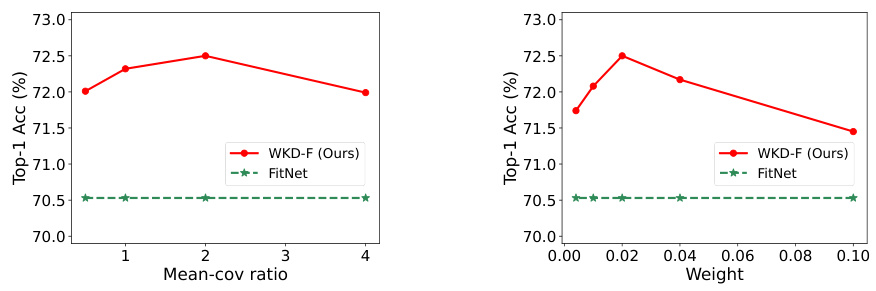
This table presents an ablation study on the feature distillation method WKD-F. It investigates several aspects of WKD-F, including different ways to model feature distributions (Gaussian, Laplace, exponential, etc.), different matching strategies (instance-wise vs. cross-instance), and different positions and grid schemes for feature distillation. The results are reported as Top-1 accuracy and the change in accuracy compared to the baseline FitNet.

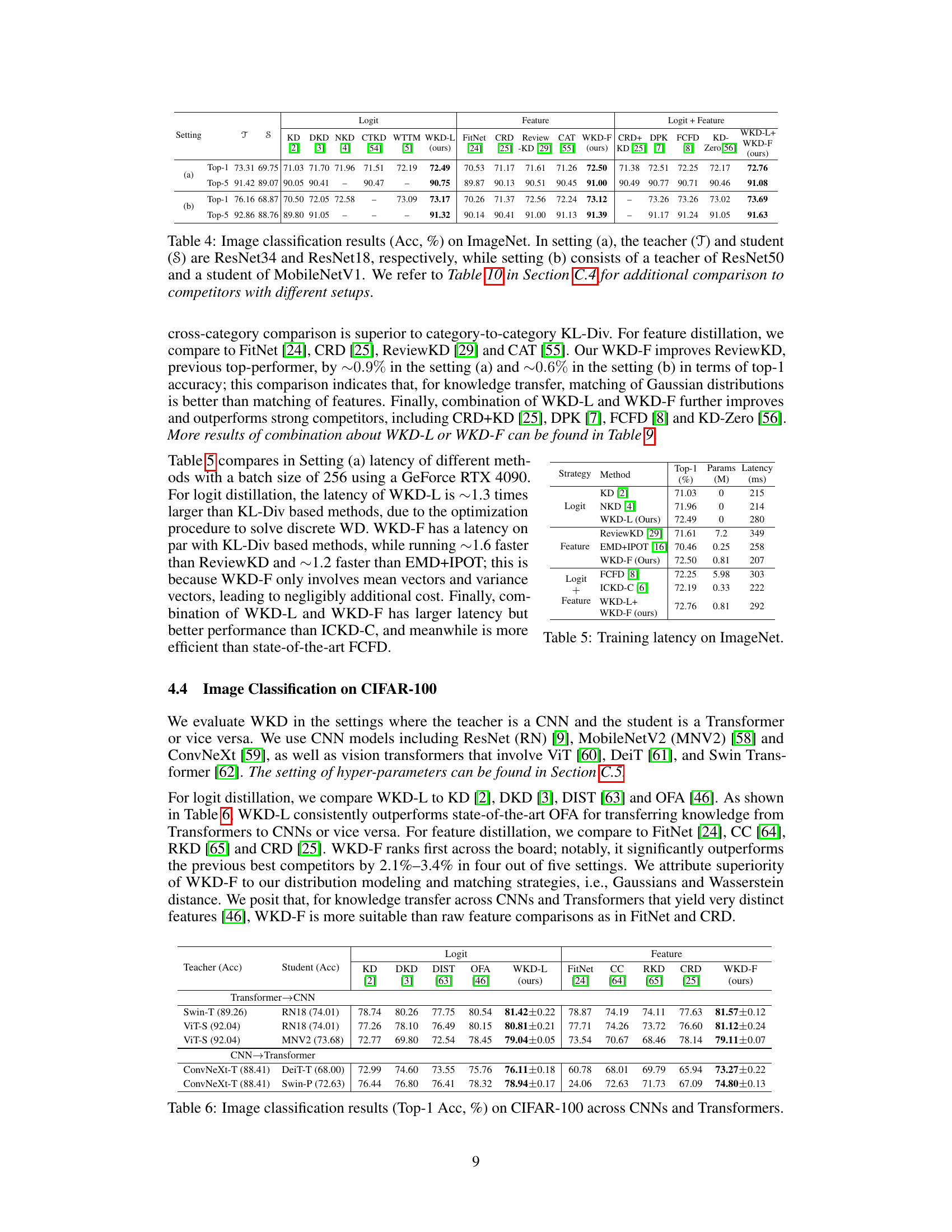
This table presents the top-1 and top-5 accuracy results for image classification on the ImageNet dataset using different knowledge distillation methods. Two experimental settings are shown: (a) where both teacher and student models use ResNet architectures (ResNet34 and ResNet18 respectively) and (b) where a ResNet50 teacher model is paired with a MobileNetV1 student model. The table compares the performance of various knowledge distillation techniques, including the proposed Wasserstein Distance-based methods (WKD-L and WKD-F), against several state-of-the-art techniques. The results demonstrate the superior performance of the proposed WKD methods, particularly when combined. Table 10 in section C.4 offers additional comparisons with competitors using varied experimental setups.
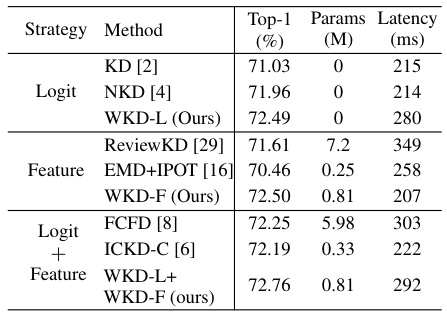
This table presents a comparison of training latency (in milliseconds) for different knowledge distillation methods on the ImageNet dataset. It compares the classical KD method with several variants, including methods that use Wasserstein distance (WD), and shows the impact of combining logit and feature distillation approaches. The model parameters (in millions) are also included to show the model complexity.
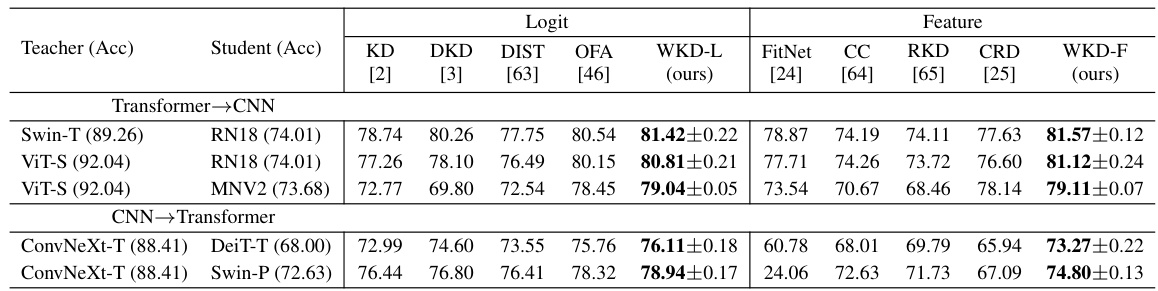
This table presents the top-1 accuracy results on the CIFAR-100 dataset for image classification using different combinations of CNNs and Transformers as teacher and student models. It compares various knowledge distillation methods, including KD, DKD, DIST, OFA, WKD-L, FitNet, CC, RKD, CRD, and WKD-F. The results are broken down by whether the teacher is a CNN or a Transformer and the corresponding student model architecture. The table demonstrates the performance of each method in different settings, allowing for a comparison of the effectiveness of various knowledge distillation approaches when transferring knowledge between different types of neural network architectures.
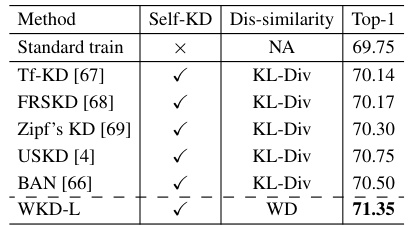
This table presents the results of self-knowledge distillation (Self-KD) experiments conducted on the ImageNet dataset using the ResNet18 architecture. It compares different methods for self-KD, including a standard training approach, several variants of knowledge distillation methods using Kullback-Leibler divergence (KL-Div), and the proposed Wasserstein Distance-based method (WKD-L). The table shows the top-1 accuracy achieved by each method, highlighting the improved performance of WKD-L compared to other methods.
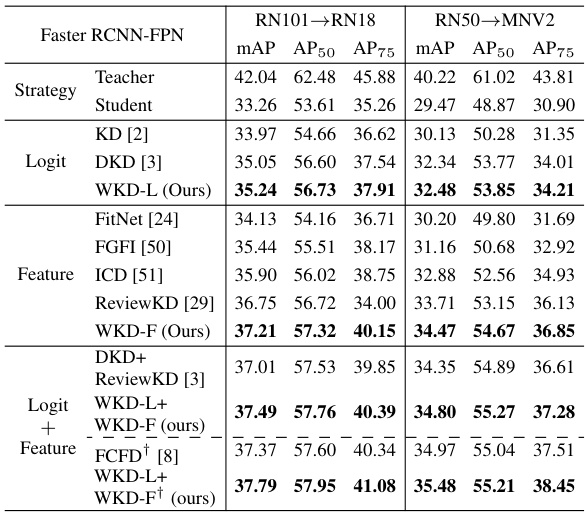
This table presents the results of object detection experiments on the MS-COCO dataset. It compares various knowledge distillation methods, including both logit and feature distillation, against several baselines (KD, DKD, FitNet, FGFI, ICD, ReviewKD, and FCFD). The table shows the mean Average Precision (mAP), AP50 (average precision at 50% IoU), and AP75 (average precision at 75% IoU) for different methods and settings. It highlights the performance improvement achieved by the proposed WKD methods, both individually and in combination.

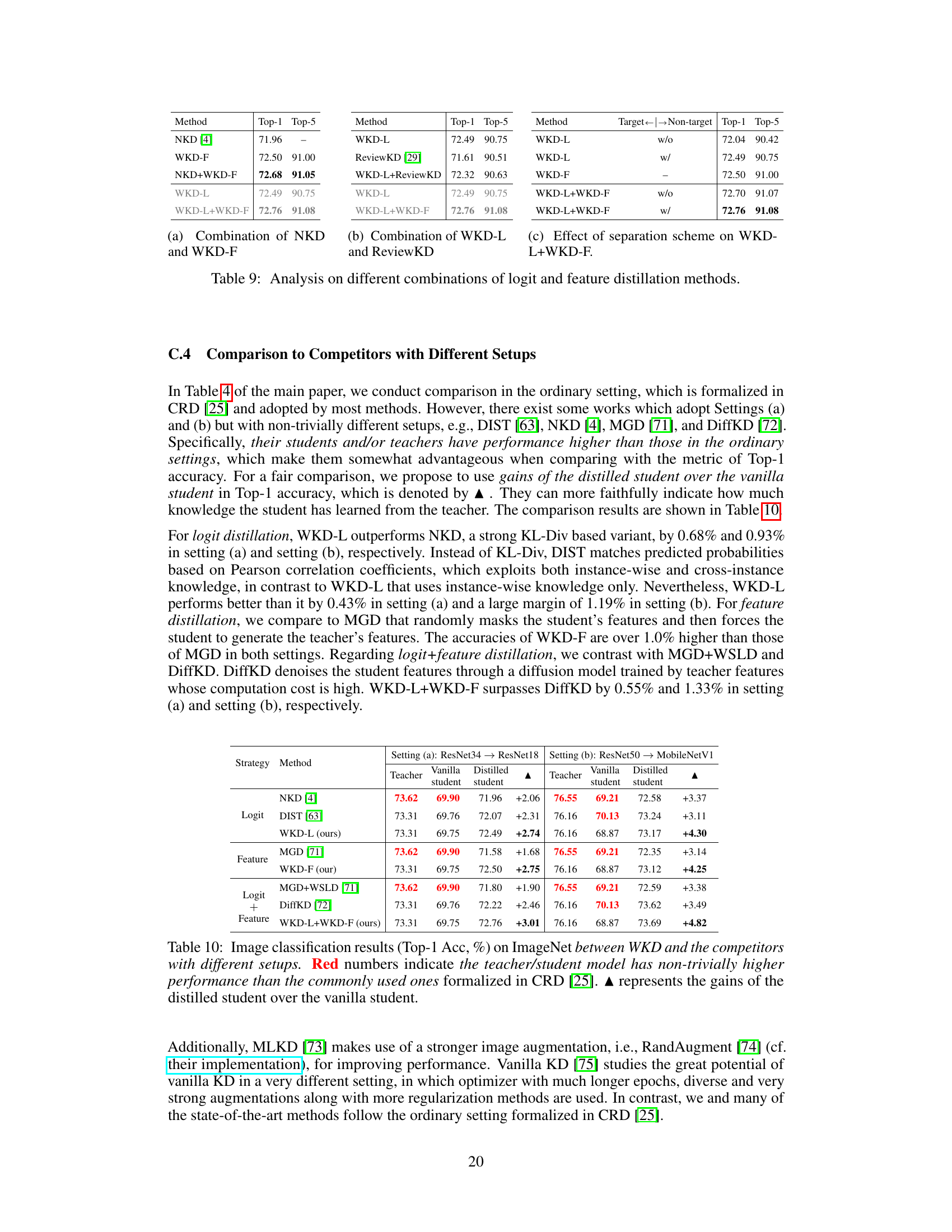
This table presents the results of experiments combining different logit and feature distillation methods. It compares the performance of using NKD (logit distillation) with WKD-F (feature distillation), WKD-L (logit distillation) with ReviewKD (feature distillation), and WKD-L with WKD-F, both with and without target/non-target separation. The results are measured by Top-1 and Top-5 accuracy.
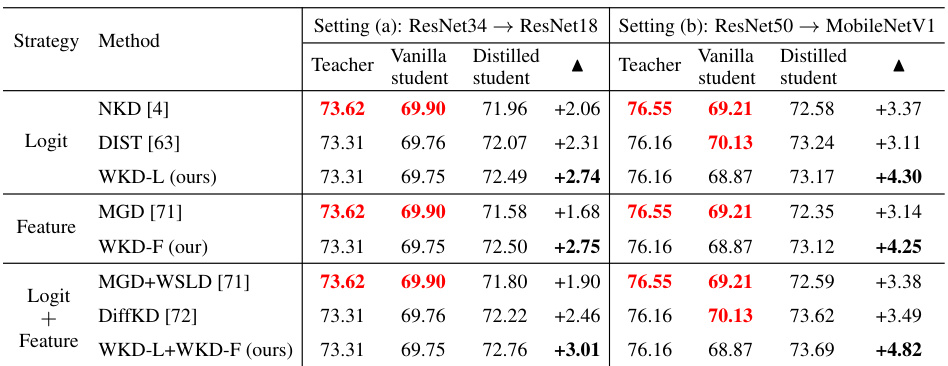
This table presents a comparison of different knowledge distillation methods on the ImageNet dataset. Two experimental settings are used: (a) ResNet34 as the teacher and ResNet18 as the student, and (b) ResNet50 as the teacher and MobileNetV1 as the student. The table shows the top-1 and top-5 accuracy for each method, including the baseline KD, and other state-of-the-art methods. The improvement over the vanilla student is also indicated. A reference to Table 10 in Section C.4 is provided for a more detailed comparison with other methods.
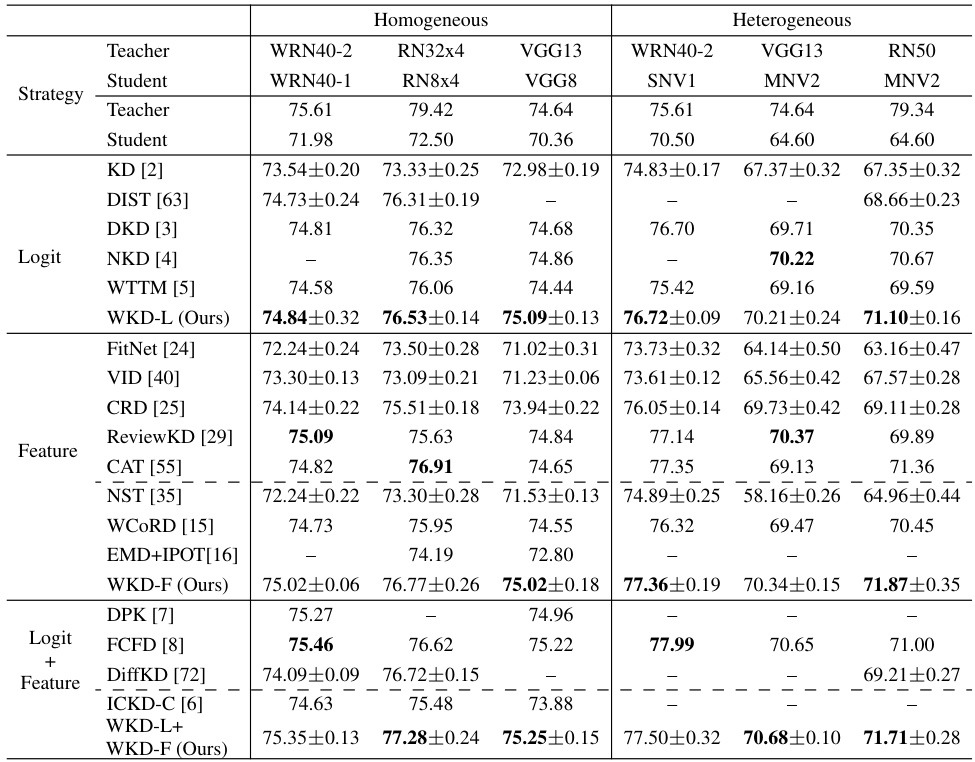
This table presents the results of image classification experiments conducted on the CIFAR-100 dataset using various CNN architectures. It compares the performance of different knowledge distillation methods (KD, DKD, DIST, NKD, WTTM, FitNet, VID, CRD, ReviewKD, CAT, WCORD, EMD+IPOT, DPK, FCFD, DiffKD, ICKD-C, and the proposed WKD-L and WKD-F methods) across different CNN architectures, showing their top-1 accuracy. Both homogeneous (teacher and student architectures are similar) and heterogeneous (teacher and student architectures are different) settings are evaluated. The table helps to understand the relative performance of various knowledge distillation techniques for image classification across diverse network architectures.

This table compares the proposed Wasserstein Distance based knowledge distillation (WKD) method with other related knowledge distillation methods. It highlights the key differences in terms of the dissimilarity measure used (KL divergence, mutual information, Wasserstein distance), whether category interrelations are considered, and the type of distillation (logit or feature). The table helps to position WKD within the existing literature and emphasizes its unique contributions.
Full paper#