↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Multi-output regression (MOR) often struggles with combinatorial distribution shift (CDS), where training data doesn’t cover all input feature combinations. This leads to poor generalization when encountering unseen combinations during testing. Existing MOR methods usually assume data from a single distribution, failing to address this critical issue.
This paper tackles CDS in MOR using a novel tensor decomposition approach. It introduces Functional t-Singular Value Decomposition (Ft-SVD), extending classical t-SVD to continuous features, and proposes a Double-Stage Empirical Risk Minimization (ERM-DS) algorithm. ERM-DS leverages the spectral properties of embeddings to capture the varying spectral decay patterns in different frequency components. The paper provides theoretical guarantees for ERM-DS under CDS, demonstrating its effectiveness and robustness.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on multi-output regression, especially those dealing with imbalanced or incomplete datasets. It introduces a novel framework to handle combinatorial distribution shift (CDS), a common but often overlooked challenge in real-world applications. The theoretical guarantees offered by the proposed algorithm enhance its reliability and open new avenues for developing robust models in various domains.
Visual Insights#

This figure illustrates the concept of Combinatorial Distribution Shift (CDS) in the context of predicting risk scores. The three axes represent age, physiological indicators/biochemical markers, and risk scores (the output). The colored area represents the combinations of input features observed in the training data. The empty corner shows that there are novel combinations of these features not covered in the training data, creating a distribution shift.

This table lists the notations used throughout the paper. It includes symbols for input and output spaces, distributions, embeddings, error terms, hypothesis classes, and algorithmic parameters. Each symbol is described and categorized based on its role in the paper’s theoretical framework and experimental results.
In-depth insights#
Ft-SVD for MOR#
The heading ‘Ft-SVD for MOR’ suggests a novel application of Functional t-Singular Value Decomposition (Ft-SVD) to the field of Multi-Output Regression (MOR). The core idea is likely to leverage the power of Ft-SVD, an extension of the traditional t-SVD, to handle high-dimensional and potentially continuous feature spaces. Ft-SVD provides a natural mathematical framework for representing multi-output functions, which is crucial in MOR where several correlated outputs need to be predicted from the same set of inputs. The method’s key advantage appears to be its ability to efficiently represent and analyze multi-output functions with complex interactions between inputs and outputs, especially when faced with limited data or combinatorial shifts in the training set. By decomposing the multi-output function into a low-rank tensor representation, Ft-SVD allows for efficient tensor completion and prediction, even in the presence of missing data or unseen feature combinations. This is achieved by exploiting the spectral properties and low-rank structure of the embeddings of the outputs in a Hilbert t-Module. The theoretical guarantees provided for the Ft-SVD-based approach enhance its reliability and make it a promising technique for addressing various challenges in MOR, including generalization to new input combinations and robustness to distribution shifts.
ERM-DS Algorithm#
The Double-Stage Empirical Risk Minimization (ERM-DS) algorithm is a novel approach designed to overcome the limitations of traditional single-stage ERM methods in handling multi-output regression problems under combinatorial distribution shifts (CDS). ERM-DS leverages a two-stage training process, first using overparameterized models to capture the complexity of the underlying functions and then using dimension reduction techniques to control overfitting and enhance generalization performance. A key strength lies in its adaptation to varying spectral decay patterns across different frequency sub-domains. This adaptive approach employs hypothesis classes tailored to each sub-domain, enabling a more precise approximation of the ground truth. The algorithm further incorporates a distillation stage, fine-tuning the reduced-rank embeddings by combining empirical risk minimization with consistency with the reduced-rank embeddings. Theoretical guarantees demonstrate its effectiveness in providing robust generalization despite the challenges posed by CDS. The use of specific hypothesis classes in each frequency component and the leveraging of spectral properties are key innovations.
CDS Challenges#
Combinatorial Distribution Shift (CDS) presents a significant challenge in multi-output regression by highlighting the limitations of training data that may not encompass all possible input feature combinations. This inability to cover all combinations leads to poor generalization on unseen feature interactions during testing. The core challenge lies in the fact that traditional methods often assume that the training and testing data share the same distribution. However, in realistic scenarios, the testing data might include novel feature interactions absent from the training data, resulting in a significant performance drop. Addressing CDS requires methods that can effectively transfer knowledge from seen feature combinations to unseen ones. This necessitates algorithms that possess robust generalization capabilities and can effectively handle the inherent variability in real-world datasets with continuous or infinite feature domains. Furthermore, understanding and modeling spectral decay patterns within the data is crucial, as it can inform efficient model design and complexity control, thus improving generalization performance in the presence of CDS.
Hilbert t-Module#
The concept of a Hilbert t-Module is crucial to this research paper, extending the idea of Hilbert spaces to handle vector-valued functions. It provides a robust mathematical framework for representing and analyzing multi-output functions in the context of multi-output regression under combinatorial distribution shifts (CDS). A key advantage of a Hilbert t-Module is its ability to capture interdependencies between multiple outputs using a t-bilinear representation. The use of the t-product, a specialized form of tensor product, allows the model to leverage the tensor structure of the data for efficient representation and computation. The inner product defined within the Hilbert t-Module facilitates calculations such as norms and inner products in a way that respects the tensor structure, enabling the development of theoretically-grounded algorithms with provable guarantees. This is a significant advancement over traditional methods which often lack such theoretical underpinnings when dealing with complex multi-output relationships.
Future Works#
The paper’s core contribution is a novel theoretical framework, Ft-SVD, for multi-output regression under combinatorial distribution shifts (CDS). Future work could focus on extending the Ft-SVD to higher-order tensors to handle more complex real-world scenarios. Empirical validation using real-world datasets across diverse domains (healthcare, marketing, etc.) is crucial to demonstrate the practical applicability of Ft-SVD and the ERM-DS algorithm. Addressing the computational cost of Ft-SVD for high-dimensional data is a key challenge. Exploring alternative optimization techniques and developing more efficient algorithms is needed. The current work rests on several assumptions; relaxing these and understanding the effects of violations is important. Finally, investigating the robustness of Ft-SVD and ERM-DS to noisy data and various types of distribution shifts beyond CDS is essential for broader applicability.
More visual insights#
More on figures
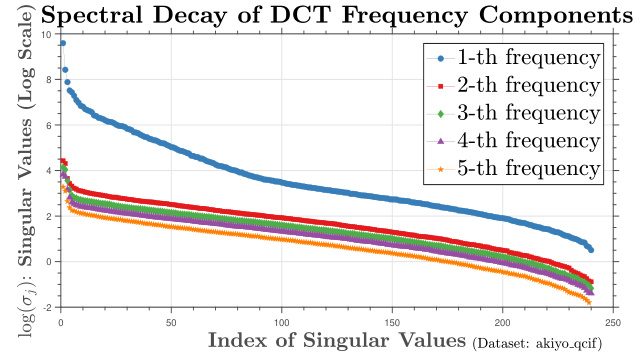
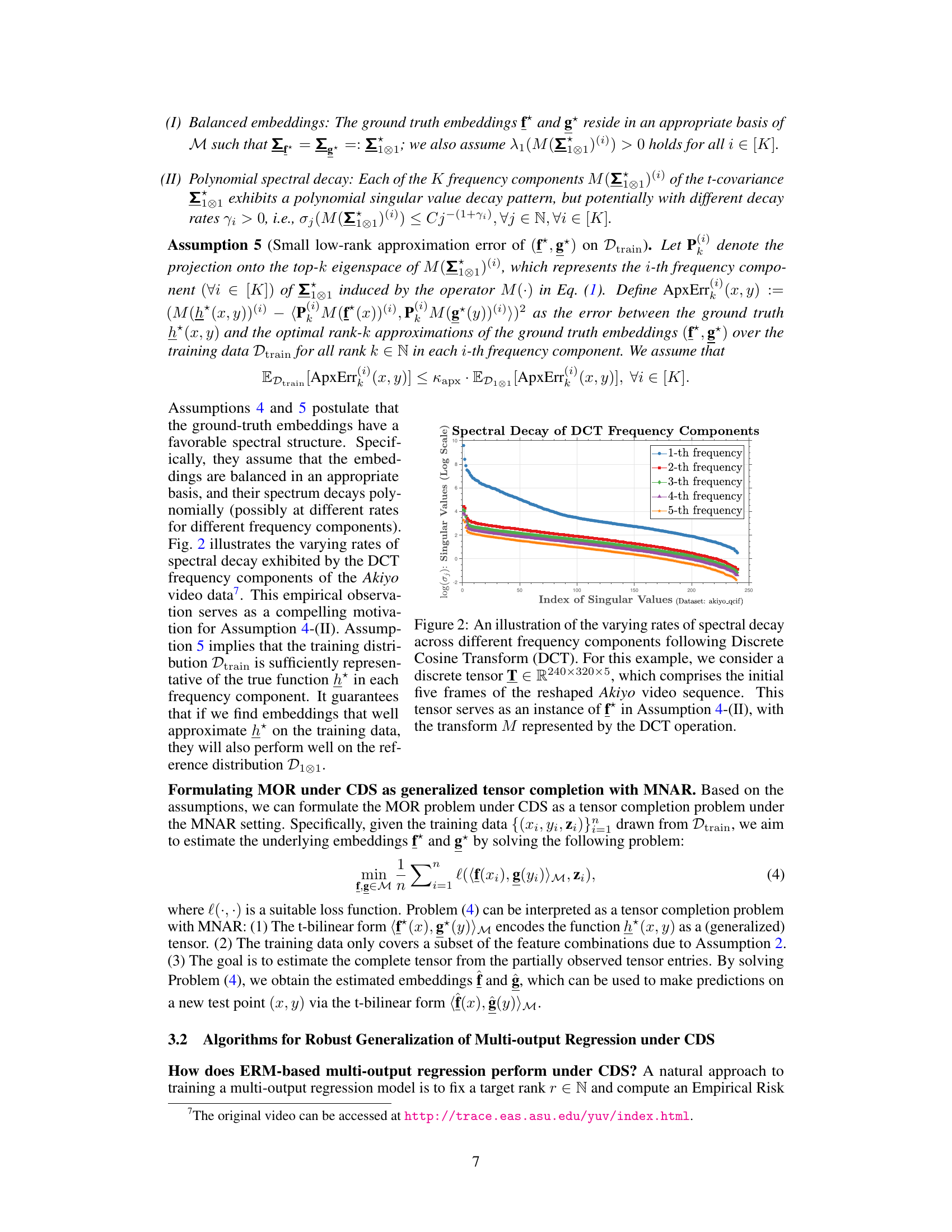
This figure shows how the singular values decay at different rates across the 5 frequency components (after DCT transformation) of the Akiyo video data. Each line represents the decay of a different frequency component of the tensor, where the tensor represents the embeddings of the ground truth function. This illustrates the varying spectral decay properties mentioned in Assumption 4-(II), which is crucial to the paper’s theoretical analysis under combinatorial distribution shift. The different decay rates across different frequency components highlight the importance of using specific hypothesis classes to better capture the varying spectral decay patterns in the proposed ERM-DS algorithm.

This figure demonstrates how the spectral decay rates vary across different frequency components (obtained using the Discrete Cosine Transform) within the context of multi-output regression under combinatorial distribution shifts (CDS). The Akiyo video data is used as an example, showcasing the diverse spectral decay patterns across different frequency components in practice. This empirical observation supports the assumption of polynomial spectral decay in the theoretical analysis.
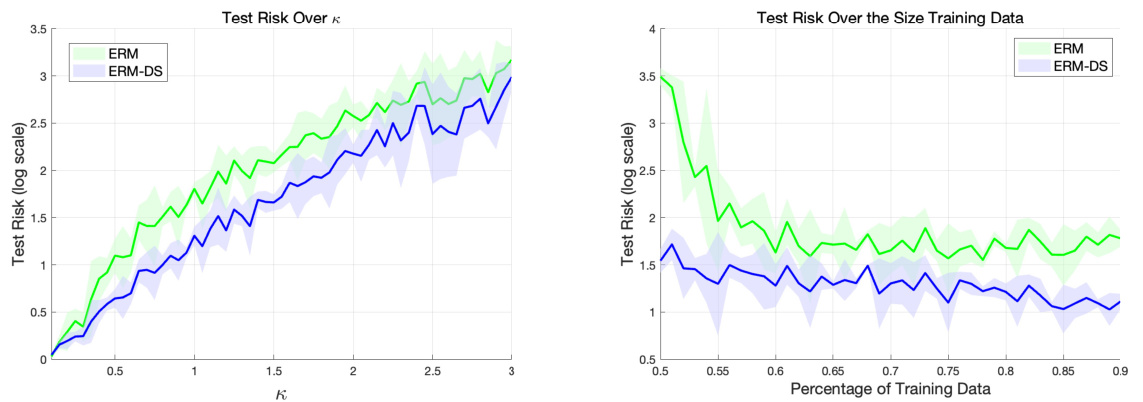
This figure demonstrates the performance of ERM and ERM-DS algorithms under varying conditions. The left panel shows how the test risk changes with increasing covariate shift intensity (κ), comparing the single-stage ERM and two-stage ERM-DS approaches. The right panel illustrates the impact of training data size on the test risk, again contrasting ERM and ERM-DS.

This figure illustrates the relationship between the core concepts of the paper. Multi-output regression under CDS motivates the development of the Ft-SVD framework, which provides a theoretical foundation for formulating the problem as tensor completion under MNAR. The Ft-SVD framework then inspires the design of the ERM-DS algorithm, which is specifically developed to address the challenges of multi-output regression under CDS.

This figure presents the results of experiments comparing the performance of two algorithms, ERM and ERM-DS, under different conditions. The left panel shows how the test risk changes as the covariate shift intensity (κ) increases, with separate results for single and double training approaches. The right panel displays the test risk as a function of the percentage of training data used, again with results for both ERM and ERM-DS. The shaded areas represent the standard deviations.
Full paper#