↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Fine-tuning large language models is crucial for various downstream tasks, but simply fine-tuning the entire model often leads to overfitting and poor generalization, especially on out-of-distribution data. The two-stage approach known as linear probing then fine-tuning (LP-FT) has emerged as a promising solution, but its underlying mechanisms require further investigation. This is particularly true for complex model architectures like Transformers.
This research addresses these issues by analyzing LP-FT’s training dynamics through the lens of Neural Tangent Kernel (NTK) theory. The NTK analysis reveals that LP-FT’s success stems from a combination of accurate predictions and increased linear head norms achieved during the linear probing stage. This increased norm effectively minimizes feature changes during fine-tuning, improving generalization. However, the study also reveals a potential trade-off: increased linear head norms can negatively affect model calibration, which the authors suggest can be addressed through temperature scaling. Finally, the study expands the NTK analysis to the LoRA method, providing further theoretical validation for its efficacy.
Key Takeaways#
Why does it matter?#
This paper is crucial because it offers a novel theoretical analysis of a widely used fine-tuning method (LP-FT), enhancing our understanding of its effectiveness and providing insights for model calibration. Its findings are significant for researchers working with large language models, especially in scenarios involving limited data or out-of-distribution generalization.
Visual Insights#
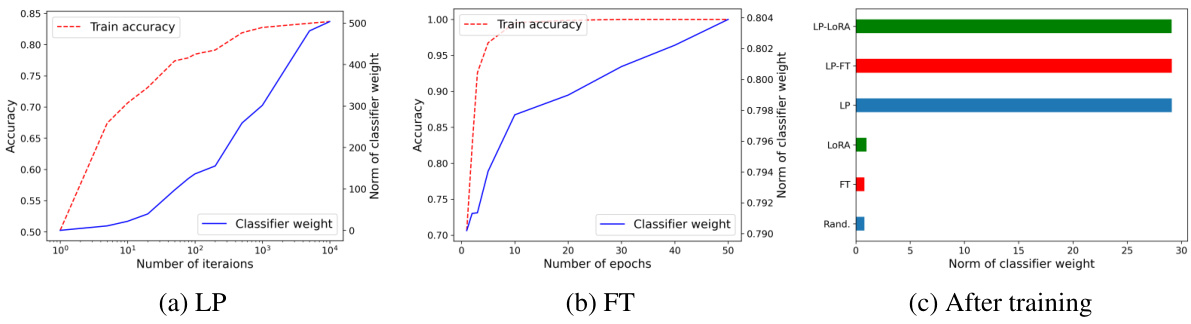
This figure shows the increase in classifier weight norms during training for three different methods: LP, FT, and LORA. The plots show how the norm of the classifier weights and training accuracy change over the number of iterations (LP) or epochs (FT). The third subplot (c) shows a comparison of the classifier weight norms after training, highlighting the significant increase in norm achieved by LP compared to FT and LORA.

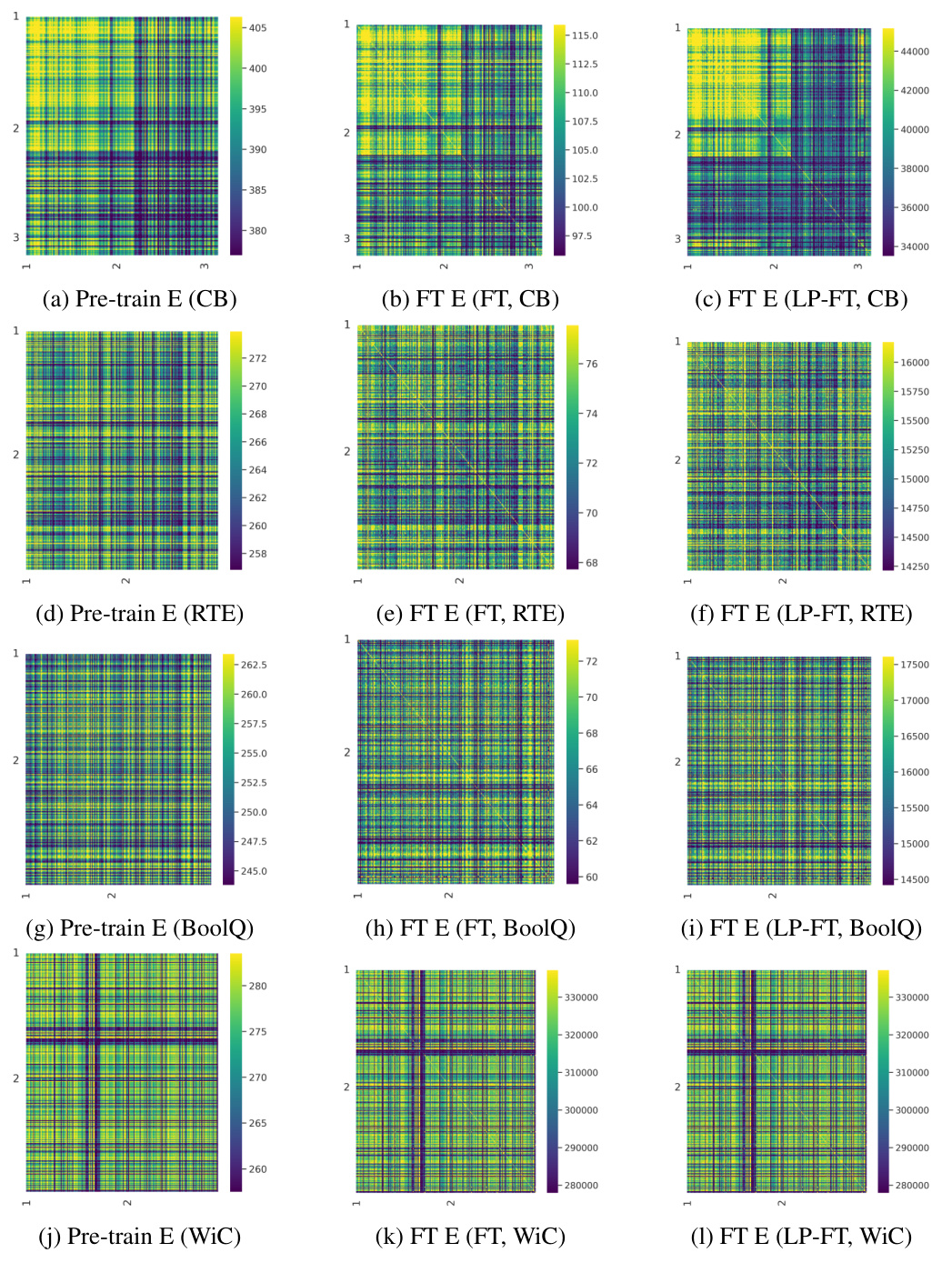
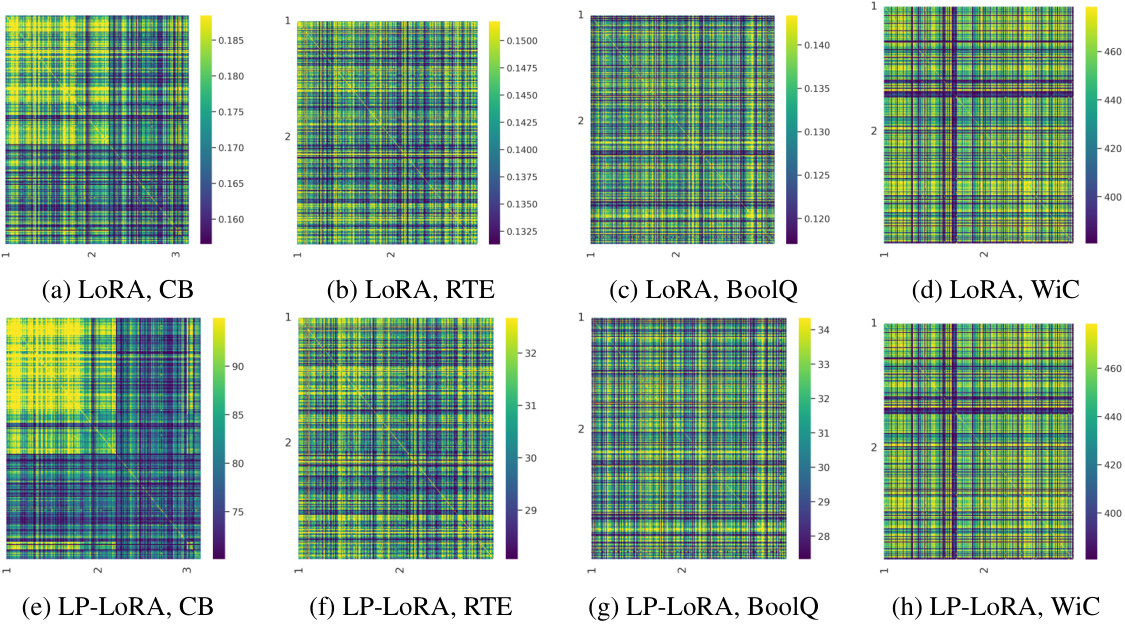
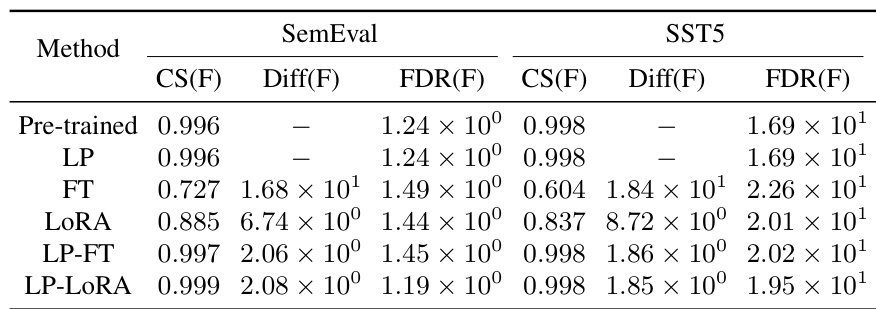
This table shows the changes in feature and classifier norms for different fine-tuning methods (LP, FT, LORA, LP-FT, LP-LORA) on two datasets (CB and RTE). It compares cosine similarity (CS), norm difference (Diff), Fisher discriminant ratio (FDR), and norm (Norm) for both features and classifiers. Key finding is LP-FT and LP-LORA show smaller feature changes and larger classifier norm increases compared to FT and LORA.
In-depth insights#
LP-FT’s NTK Dynamics#
Analyzing LP-FT’s training dynamics through the lens of Neural Tangent Kernel (NTK) theory offers valuable insights. The NTK framework allows for a decomposition of the learning process into pre-train and fine-tuning components, highlighting how LP-FT’s two-stage approach interacts with the model’s feature space. Linear probing’s role is crucial in establishing a near-optimal linear head, which is then leveraged during fine-tuning to minimize feature distortion. The analysis reveals the importance of the linear head norm’s increase during linear probing; this norm increase reduces feature changes during fine-tuning and improves out-of-distribution generalization. However, the study also indicates a potential calibration issue stemming from this increased norm, suggesting temperature scaling as a possible corrective measure. The NTK perspective provides a quantitative framework to understand the complex interplay between linear probing, fine-tuning, and feature preservation, offering insights for optimizing language model adaptation strategies.
Linear Head’s Role#
The linear head plays a crucial role in the effectiveness of linear probing then fine-tuning (LP-FT). Its near-optimal optimization during the linear probing (LP) stage is key, preserving pre-trained features and minimizing feature distortion during the subsequent fine-tuning (FT) stage. The increase in the linear head’s norm during LP, stemming from cross-entropy loss, further contributes to this feature preservation. However, this increased norm can negatively impact model calibration, leading to overconfident predictions which can be mitigated by temperature scaling. The interplay between prediction accuracy and the linear head’s norm at the start of FT is highlighted, emphasizing the importance of the LP stage in setting the stage for a successful FT. The analysis further extends to low-rank adaptation (LoRA), validating its efficacy and similarity to LP-FT in minimizing feature changes within the NTK regime.
Calibration Effects#
Calibration, in the context of machine learning models, refers to the reliability of predicted probabilities. A well-calibrated model produces predictions where a 90% confidence score accurately reflects that the model is correct 90% of the time. This research explores how the linear probing then fine-tuning (LP-FT) method affects model calibration. The authors observe that while LP-FT is effective in reducing feature distortion and improving generalization, the increased norm of the linear head during linear probing can negatively impact calibration. This effect manifests as overconfident predictions, where the model assigns higher probabilities than are justified by its actual performance. Importantly, the study proposes temperature scaling as a simple yet effective method to correct this calibration issue, demonstrating its ability to improve the alignment between predicted probabilities and actual outcomes. Therefore, while LP-FT may enhance accuracy, careful attention to the calibration aspect is crucial, and techniques like temperature scaling are vital for ensuring reliability and responsible deployment of these models.
LoRA’s Efficacy#
The effectiveness of LoRA (Low-Rank Adaptation) in fine-tuning large language models is a significant area of research. LoRA’s parameter efficiency is a key advantage, making it suitable for resource-constrained environments. By updating only a small subset of parameters, LoRA avoids the computational cost and potential instability associated with full fine-tuning. However, LoRA’s performance is highly dependent on hyperparameter tuning, including the rank and scaling factor of the low-rank update matrices. Improper tuning can lead to suboptimal results or even performance degradation. The impact of the rank parameter, in particular, deserves further investigation. A higher rank increases the number of trainable parameters and may lead to improved performance but also increases computational requirements. Ultimately, a comprehensive evaluation of LoRA’s efficacy requires careful consideration of the specific application, dataset, and model architecture, alongside diligent hyperparameter optimization.
Future Work#
Future research directions stemming from this work could explore several promising avenues. Extending the NTK analysis to other architectures beyond Transformers would broaden the applicability and generalizability of the findings. Investigating the impact of different loss functions on feature distortion could further refine the understanding of LP-FT’s mechanisms. A deeper dive into the interplay between the increased linear head norm and model calibration, especially in addressing potential overconfidence, is warranted. This includes exploring alternative calibration techniques beyond temperature scaling. Finally, empirical evaluation on a wider range of NLP tasks and datasets, particularly those involving low-resource scenarios, is needed to fully assess the robustness and effectiveness of LP-FT. Additionally, research into the practical implications and limitations of LP-FT in real-world deployment would significantly enhance its impact.
More visual insights#
More on figures

This figure displays the distribution of singular values of the NTK matrix for different training methods on the CB dataset. Each line represents a different training method (Pre-train E, FT, LP-FT, LORA, LP-LORA). The singular values are normalized by the maximum singular value to allow for easier comparison across methods. The plot shows the distribution of singular values for the pre-train-effective and FT-effective components of the NTK matrix. The pre-train-effective component is similar across all methods, while the FT-effective component differs depending on the method.
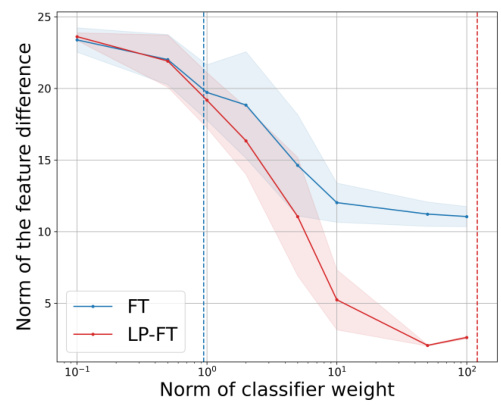
This figure shows the impact of classifier weight norm on feature changes during fine-tuning, specifically focusing on the SST-5 dataset (out-of-distribution). The x-axis represents the norm of the classifier weight after training, while the y-axis represents the norm of the feature difference (the change in features). Two lines are plotted: one for fine-tuning (FT) alone and one for linear probing then fine-tuning (LP-FT). Shaded regions represent standard errors, highlighting the uncertainty in the measurements. The plot demonstrates that as the classifier weight norm increases, the norm of the feature difference decreases, which is more pronounced in LP-FT compared to FT. This supports the paper’s claim that LP-FT leads to reduced feature changes due to the increase in the classifier weight norm during linear probing.
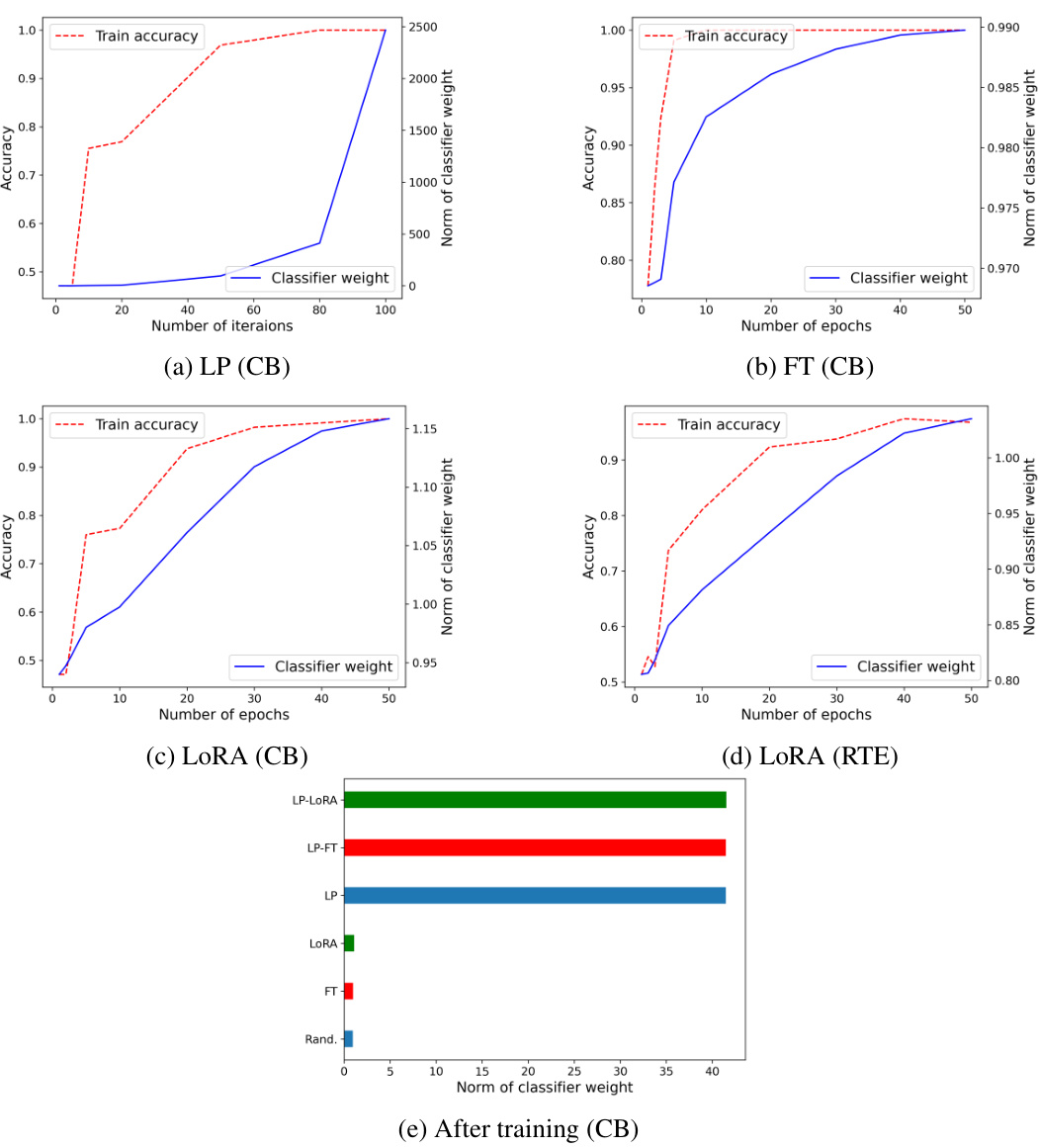
This figure shows the increase in classifier weight norms during the training process on the RTE dataset for three different fine-tuning methods: Linear Probing (LP), Fine-tuning (FT), and LP-FT (Linear Probing then Fine-tuning). Subfigure (a) displays the training dynamics of LP showing the increase in both accuracy and classifier weight norm. Subfigure (b) shows the same for FT. Finally, subfigure (c) compares the final classifier weight norms after training for all three methods, highlighting the significantly larger norm achieved by LP-FT.
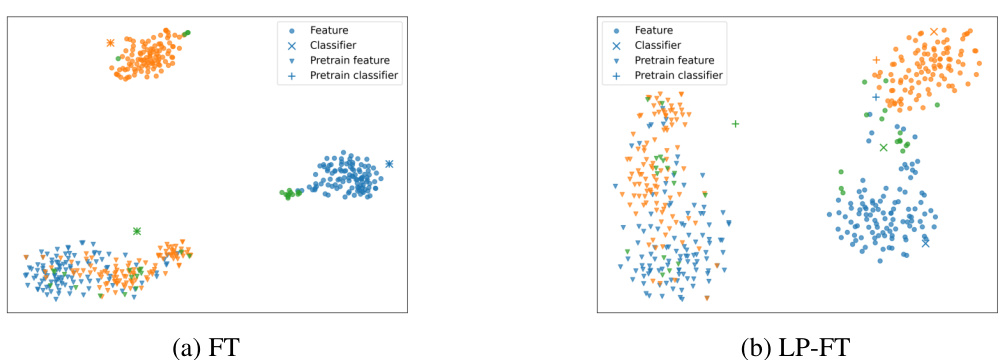
This figure uses t-SNE to visualize the feature vectors (penultimate layer) and classifier weights of a model trained on the CB dataset using two different methods: standard fine-tuning (FT) and linear probing then fine-tuning (LP-FT). In (a), standard FT shows clearly separated feature clusters by class, but classifier weights remain close to the initial pretrained weights. In (b), LP-FT shows that feature clusters maintain a similar structure to the pretrained model, while classifier weights have notably shifted from their initial state. This visualization supports the paper’s claim that LP-FT causes smaller changes to features during training than standard FT while significantly altering classifier weights.
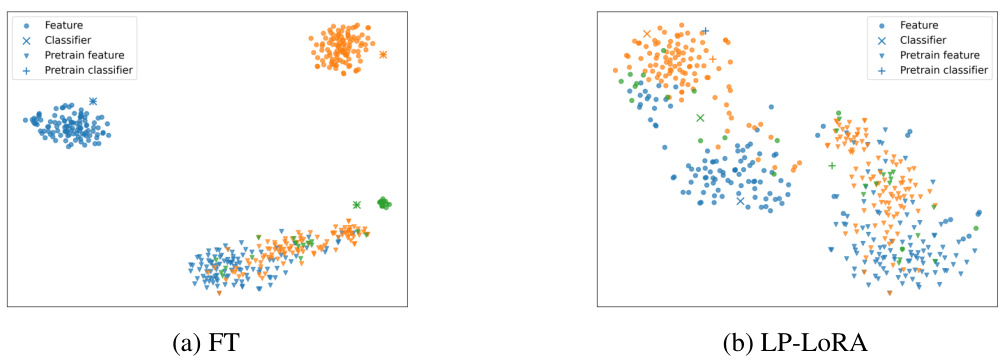
This figure uses t-SNE to visualize the changes in features and classifier weights after fine-tuning (FT) and linear probing then fine-tuning (LP-FT). Panel (a) shows that standard FT leads to clear separation of features by class, but the classifier weights remain close to their pre-trained values. Panel (b) demonstrates that LP-FT preserves the structure of the pre-trained features while substantially altering the classifier weights. This visually supports the paper’s claim that LP-FT minimizes feature changes while effectively optimizing the linear head.
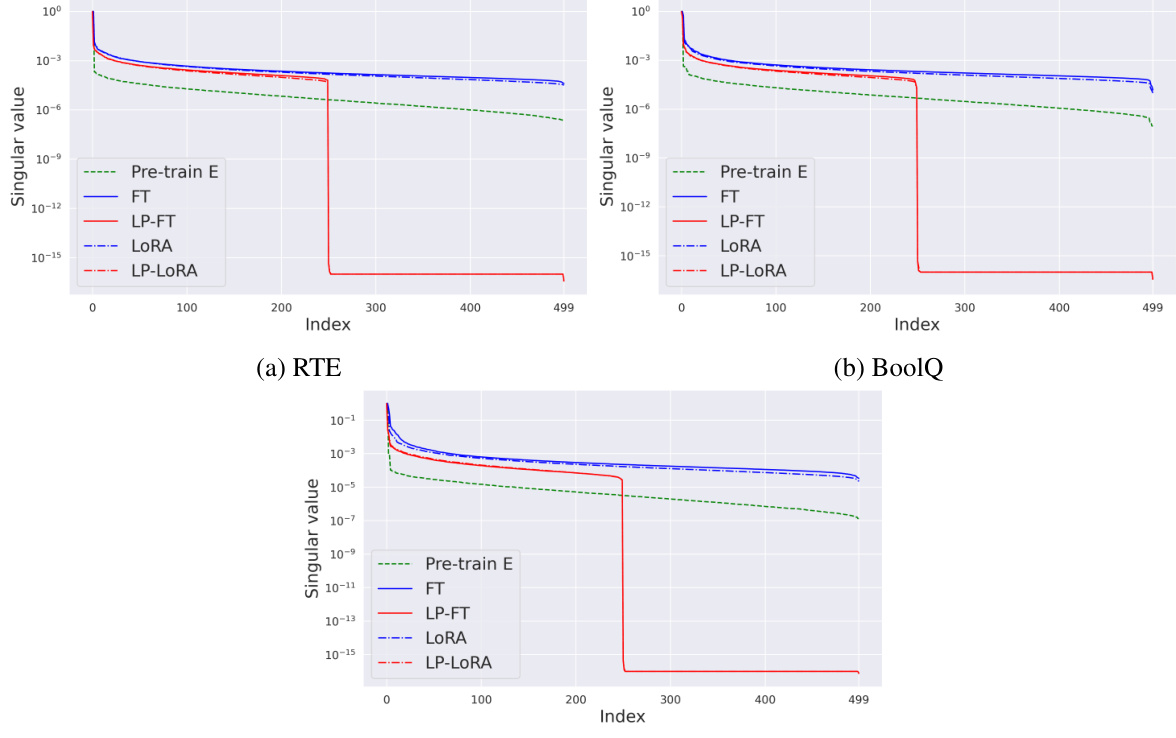
This figure shows the distribution of singular values for the NTK matrices obtained through different fine-tuning methods (FT, LP-FT, LoRA, LP-LORA) and the pre-trained model on three different datasets (RTE, BoolQ, WiC). The singular values are normalized by the maximum singular value. The plot visually illustrates how the singular value distribution changes with different fine-tuning strategies and datasets, providing insights into the training dynamics and feature extraction.
This figure visualizes the increase in classifier weight norms during the training process on the RTE dataset using three different methods: LP (linear probing), FT (fine-tuning), and LP-FT (linear probing then fine-tuning). The plots show that the classifier weight norms increase over the training iterations/epochs for all methods, but significantly more for LP-FT than other methods. This indicates how the LP-FT strategy optimizes the linear head during the LP stage, resulting in a large increase in the norm at the beginning of the FT stage. This phenomenon is linked to the reduction of feature changes, and is considered one of the reasons for LP-FT’s high performance.
This figure shows the increase in classifier weight norms during training on the RTE dataset. The left panel (a) displays the increase in training accuracy and classifier weight norm during linear probing (LP). The middle panel (b) shows the same during fine-tuning (FT). Finally, the right panel (c) shows the final classifier weight norms after the training is complete. The figure demonstrates that the classifier weight norm increases during both LP and FT stages.

This figure shows how the classifier weights’ norms change during the training process of different fine-tuning methods on the RTE dataset. It visually represents three key observations: 1. Increase in Norm: The norm of the classifier weights increases notably during training for LP, FT, and LP-FT. This highlights the impact of training on the model’s linear head. 2. Accuracy Correlation: The increase in classifier weight norm is correlated with improvements in training accuracy for each method. This shows the linear head’s optimization plays a key role in performance. 3. Post-Training Norms: The final classifier weight norms after training (panel (c)) reveal that LP-FT results in classifier weights with higher norms compared to FT alone. This suggests that LP-FT better preserves pre-trained features while achieving improved performance.

This figure shows the impact of classifier weight norm on feature changes during fine-tuning. The SST-5 dataset (out-of-distribution) was used for this experiment. The y-axis represents the norm of feature difference and x-axis represents the norm of classifier weight. The solid lines show average values and shaded area represents standard errors. As the norm of classifier weight increases, the norm of feature difference decreases, supporting the paper’s analysis that a higher classifier weight norm reduces feature distortion.
More on tables

This table presents the results of kernel analysis performed on the CB dataset, focusing on the neural tangent kernel (NTK) matrix and its decomposition into pre-train and fine-tuning effective components. It shows the Frobenius norm (FN), kernel regression accuracy (Acc) on training and test sets, and the FT ratio (representing the contribution of the FT-effective component). The table helps understand the relative contributions of pre-trained features and fine-tuning updates to the model’s performance.

This table presents the Expected Calibration Error (ECE) and Maximum Calibration Error (MCE) for four different fine-tuning methods (FT, LP-FT, LoRA, LP-LoRA) on the RTE dataset, both with and without temperature scaling. The improvement in calibration due to temperature scaling is shown. The results highlight the potential of mitigating poor calibration in LP-FT through temperature scaling.

This table presents a quantitative comparison of changes in feature and classifier norms after different fine-tuning methods (FT, LP-FT, LORA, LP-LORA) on two datasets: CB and RTE. It shows that LP-FT, compared to standard fine-tuning (FT), leads to smaller changes in the features (as measured by CS, Diff, and FDR) while maintaining a significantly larger increase in the classifier norm. This pattern is also observed when using the LoRA parameter-efficient fine-tuning method.
This table shows a comparison of changes in feature and classifier norms for different fine-tuning methods (FT, LP-FT, LORA, LP-LORA) on two datasets (CB and RTE). It demonstrates that linear probing then fine-tuning (LP-FT) and LoRA methods lead to smaller changes in pre-trained features while significantly increasing the classifier norm compared to standard fine-tuning.

This table shows the hyperparameter settings used in the experiments for different fine-tuning methods (FT, LoRA, LP-FT, and LP-LORA) and datasets. For each dataset and method, it specifies the batch size (bs), learning rate (lr), alpha (α, for LoRA and LP-LORA), and rank (r, for LoRA and LP-LORA) used during training. These settings were optimized to achieve good performance on the validation sets.
This table shows the changes in features and classifier norms before and after different fine-tuning methods (LP, FT, LORA, LP-FT, LP-LORA) on the CB and RTE datasets. It demonstrates that LP-FT effectively minimizes changes in pre-trained features while significantly increasing the classifier norm, which aligns with the paper’s findings on feature preservation and the impact of classifier weight norms.

This table presents a quantitative comparison of changes in features and classifier norms after different fine-tuning methods (LP, FT, LORA, LP-FT, LP-LORA) on two datasets (CB and RTE). It shows that LP-FT successfully minimizes changes to pre-trained features while significantly increasing the norm of the classifier. This supports the paper’s claim that LP-FT preserves beneficial pre-trained features and benefits from a larger classifier norm.
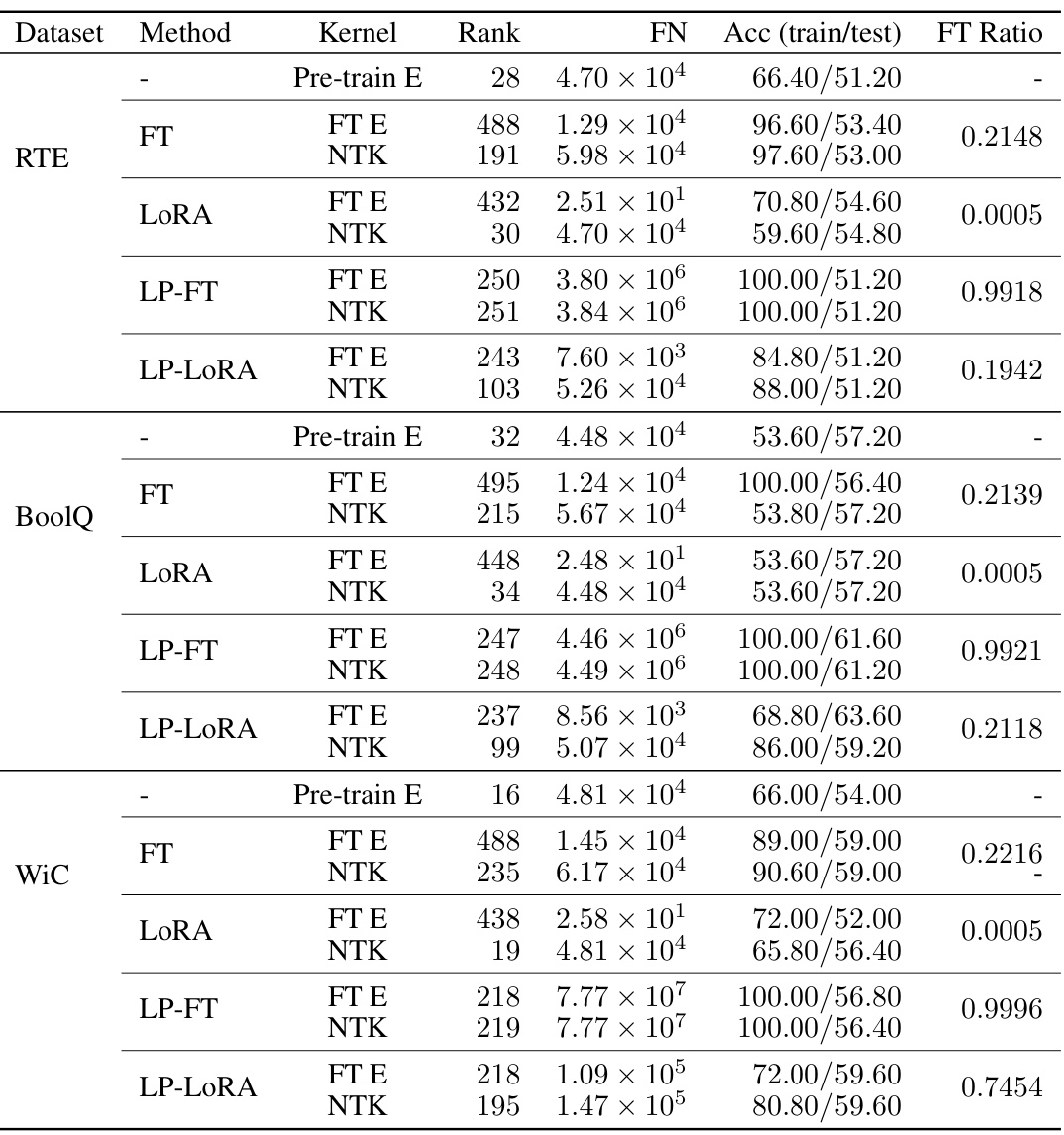
This table presents the kernel statistics for the CB dataset, comparing different fine-tuning methods (FT, LoRA, LP-FT, LP-LORA). It shows the Frobenius norm (FN), kernel regression accuracy (Acc), and the contribution of the FT-effective component (FT Ratio) to the overall kernel for each method. Pre-train E and FT E columns represent the pre-train-effective and FT-effective components of the NTK matrix respectively, providing insights into the relative influence of pre-trained features and fine-tuning on prediction accuracy.

This table presents the results of experiments conducted on the BOSS benchmark to evaluate the performance of different fine-tuning methods. The accuracy and standard deviation are reported for both in-distribution (ID) and out-of-distribution (OOD) data, across four different datasets: Amazon, Dynasent, SemEval, and SST-5. The best performing method for each dataset and setting is highlighted in bold, indicating the superior performance of LP-FT in many cases. The results showcase that the two-stage approach of linear probing followed by fine-tuning generally improves performance compared to other methods.

This table presents a quantitative comparison of changes in features and classifier norms after different fine-tuning methods (FT, LP-FT, LORA, LP-LORA) on two datasets (CB and RTE). The results demonstrate that linear probing then fine-tuning (LP-FT) results in smaller changes to pre-trained features while significantly increasing the classifier norm compared to standard fine-tuning. The low-rank adaptation (LoRA) method shows a similar trend.
This table shows a comparison of changes in features and classifier norms after different fine-tuning methods (LP, FT, LORA, LP-FT, LP-LORA) on two datasets (CB and RTE). It highlights that LP-FT and LP-LORA result in smaller changes to pre-trained features while significantly increasing the classifier norm, suggesting a balance between preserving pre-trained information and adapting the linear classifier.

This table presents a quantitative comparison of changes in features and classifier norms for different fine-tuning methods (FT, LP-FT, LORA, LP-LORA) on two datasets (CB and RTE). It shows that LP-FT leads to smaller changes in features compared to standard FT while maintaining similarity to pre-trained features and achieving a larger increase in classifier norm. The results also suggest that these trends hold when utilizing LoRA.

This table presents a quantitative comparison of changes in feature and classifier norms between different fine-tuning methods (FT, LP-FT, LORA, LP-LORA) for two datasets (CB and RTE). It shows that LP-FT effectively minimizes changes to pre-trained features while significantly increasing the classifier norm, which is also observed with LoRA. The metrics used are cosine similarity (CS), norm difference (Diff), Fisher’s discriminant ratio (FDR), and norm (Norm).
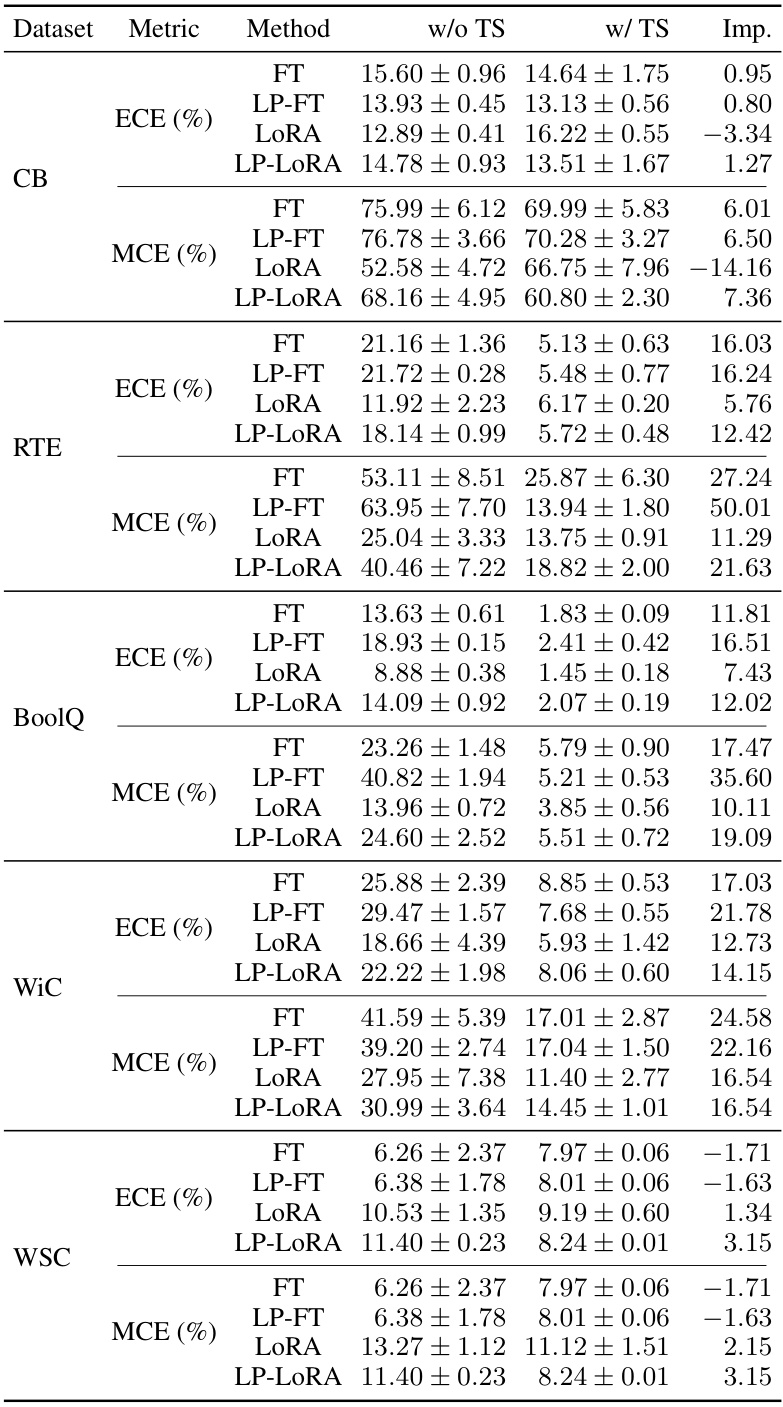
This table presents a quantitative comparison of changes in feature and classifier norms for different fine-tuning methods (FT, LP-FT, LORA, LP-LORA) on two datasets (CB and RTE). It shows that LP-FT effectively preserves pre-trained features while significantly increasing the classifier norm. This observation supports the paper’s argument about the role of the classifier norm in LP-FT’s success.
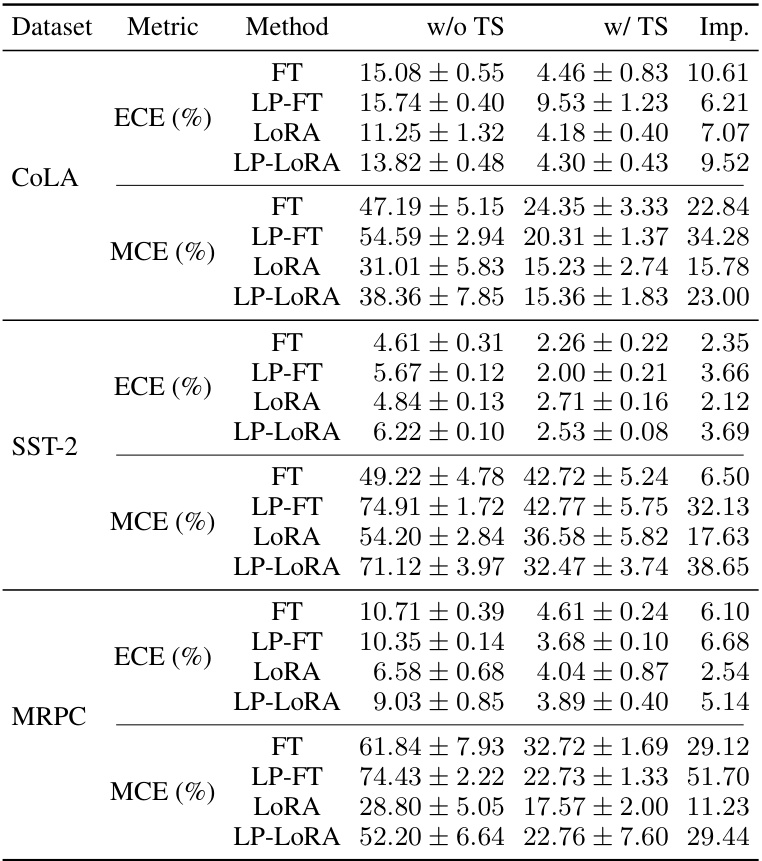
This table presents a quantitative comparison of changes in feature and classifier norms for different fine-tuning methods (FT, LP-FT, LORA, LP-LORA) on two datasets (CB and RTE). It shows that LP-FT and LP-LORA result in smaller changes to the pre-trained features (indicated by lower Diff(F) and higher CS(F), demonstrating better feature preservation. However, these methods also show a significantly larger increase in the classifier norm (Norm(C)), highlighting a key trade-off observed in the study.

This table shows a comparison of changes in features and classifier norms after different fine-tuning methods (FT, LP-FT, LORA, LP-LORA) on the CB and RTE datasets. It demonstrates that LP-FT effectively minimizes feature changes while significantly increasing the classifier norm, supporting the paper’s core argument.
Full paper#



















