↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Current uncertainty quantification methods are computationally expensive and memory-intensive, particularly for deep neural networks with high parameter counts. This prevents their practical use in many applications. Existing methods either train multiple models or approximate the Fisher information matrix, both of which are limited in scalability. The high memory cost is a major bottleneck. This paper addresses these issues by introducing a novel uncertainty score, called SLU (Sketched Lanczos Uncertainty).
SLU combines Lanczos’ algorithm with dimensionality reduction techniques. It computes a sketch of the leading eigenvectors of the Fisher information matrix using a small memory footprint. This approach only requires logarithmic memory, in contrast to existing techniques requiring linear memory. Empirically, SLU demonstrates well-calibrated uncertainties, reliably identifies out-of-distribution samples, and significantly outperforms existing methods in terms of accuracy while consuming considerably less memory. The algorithm’s error is provably bounded and the improved performance is shown in various experiments.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on uncertainty quantification in deep learning, particularly those dealing with high-dimensional models. It offers a novel, memory-efficient solution for computing uncertainty scores, which is a significant challenge in the field. The proposed method, based on sketched Lanczos algorithms, opens new avenues for improving the scalability and reliability of uncertainty estimation in various applications, enabling researchers to tackle larger, more complex models. The approach’s provable error bounds and empirical improvements over existing methods make it a valuable contribution with practical implications.
Visual Insights#

The figure shows the AUROC (Area Under the Receiver Operating Characteristic curve) scores for out-of-distribution (OoD) detection on a ResNet model. It compares the performance of different uncertainty quantification methods: Randomized SVD, Vanilla Lanczos, and Sketched Lanczos (with two different sketch sizes). The x-axis represents the memory cost in the number of neural networks, and the y-axis shows the AUROC score. The results indicate that Sketched Lanczos, particularly with a larger sketch size (s=100000), achieves higher AUROC scores while using less memory compared to the other methods. This demonstrates the memory efficiency and effectiveness of the proposed Sketched Lanczos algorithm for uncertainty quantification.

This table compares the time and memory complexities of three sketching methods: Dense JL, Sparse JL, and SRFT. The complexities are given in terms of p (the dimension of the high-dimensional space), s (the sketch size), and ε (the desired accuracy). The table shows that SRFT offers a favorable trade-off between time and memory complexity, particularly for large p.
In-depth insights#
Lanczos Sketching#
Lanczos sketching, a core technique in the paper, cleverly combines the Lanczos algorithm for eigenvalue approximation with dimensionality reduction via sketching. The brilliance lies in its ability to drastically reduce memory consumption by sketching Lanczos vectors during the iterative process instead of storing the entire matrix. This makes it feasible to apply the method to large-scale models where traditional methods fail due to memory limitations. The algorithm maintains accuracy by employing orthogonalization post-hoc on the sketched vectors, mitigating the effects of sketching-introduced noise and ensuring well-calibrated uncertainty estimates. This method thus offers a practical balance between accuracy and efficiency, a vital advancement in the field of uncertainty quantification. The theoretical justification for this trade-off between memory and accuracy is rigorously established, demonstrating the robustness and scalability of the approach.
Low-memory Score#
The concept of a “low-memory score” in the context of a research paper likely refers to a method for calculating a score or metric that requires minimal memory resources. This is particularly important in machine learning, where models can have millions or even billions of parameters, making traditional methods for uncertainty quantification computationally expensive. A low-memory score would be designed to address this challenge. The key innovation might lie in clever algorithmic techniques or approximations that enable the score calculation without storing the entire model’s parameters or large intermediate matrices. This could involve techniques like dimensionality reduction, sketching, or sparse matrix operations. A well-designed low-memory score would need to balance memory efficiency with accuracy and reliability, ensuring that the resulting score is a faithful representation of the underlying uncertainty, even with the computational constraints. This type of work is significant because it enables the application of sophisticated uncertainty quantification methods to larger and more complex models that were previously intractable due to memory limitations.
OoD Detection#
The paper investigates out-of-distribution (OoD) detection as a key application of its proposed uncertainty quantification method. OoD detection aims to identify data points that differ significantly from the distribution the model was trained on. The method’s effectiveness in OoD detection is empirically evaluated against various baselines and datasets, demonstrating its superior performance, especially in low-memory regimes. This success stems from the method’s ability to provide well-calibrated uncertainty scores, which are crucial for effectively distinguishing in-distribution from out-of-distribution samples. The low memory footprint is a significant advantage, allowing the method to scale to larger models where traditional uncertainty quantification methods become computationally infeasible. The paper highlights the importance of a balance between uncertainty estimation accuracy and computational cost, particularly in resource-constrained environments. The results suggest that the proposed method offers a promising solution for improving the robustness and reliability of machine learning models in real-world applications where encountering OoD data is inevitable.
Algorithm Analysis#
A thorough algorithm analysis should dissect the computational complexity of the proposed method, quantifying time and space requirements with respect to key parameters like the number of model parameters (p), the approximation rank (k), and the sketch size (s). The analysis should rigorously establish the trade-offs between accuracy and efficiency, demonstrating how the chosen parameters impact the overall performance. Crucially, the analysis needs to address the impact of sketching, showing that the approximation error remains bounded and comparing it against alternative dimensionality reduction techniques like randomized SVD. The study of convergence properties is key; an analysis should prove that the algorithm converges to a good approximation of the desired eigen-decomposition, specifying the rate of convergence and potentially outlining conditions that ensure its efficiency. Finally, a complete analysis should compare its performance against state-of-the-art alternatives, justifying the choices made and providing compelling evidence of the new approach’s superiority in a specific context.
Future Work#
Future research could explore several promising avenues. Improving the efficiency of the sketching process, perhaps through exploring alternative sketching matrices or optimized algorithms, could be beneficial. Investigating the impact of different preconditioning strategies on accuracy and stability would be valuable. Extending the approach to different neural network architectures, especially those with complex structures like transformers, and also to different tasks such as sequential data modeling and reinforcement learning, is crucial. A deeper theoretical analysis into the relationship between the rank of the approximation and the error introduced by sketching, particularly in the context of high dimensional data, is warranted. Finally, developing a Bayesian extension that enables sampling from the approximate posterior distribution would enhance the method’s interpretability and applicability in uncertainty quantification.
More visual insights#
More on figures

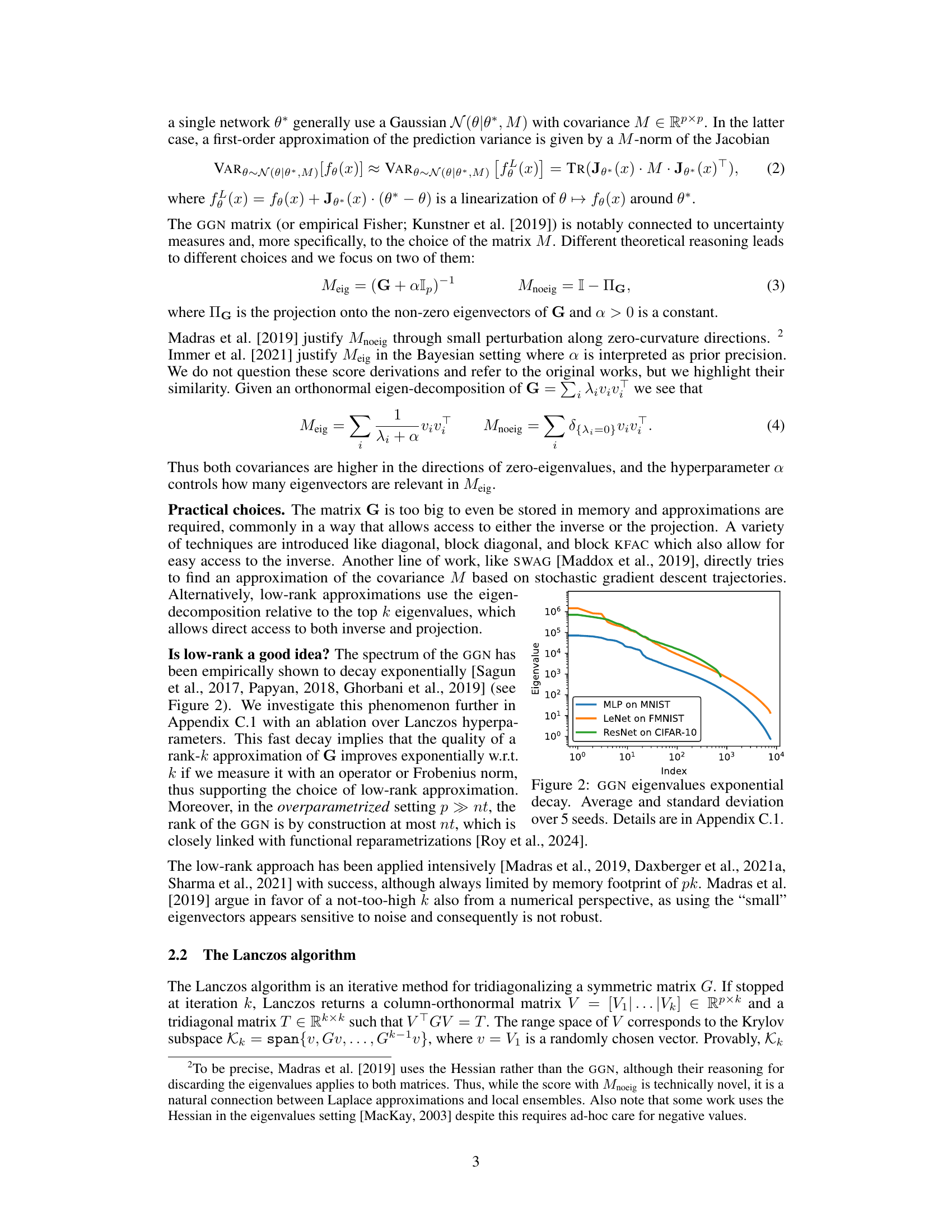
This figure shows the exponential decay of Generalized Gauss-Newton (GGN) matrix eigenvalues for three different neural network architectures trained on different datasets. The x-axis represents the index of the eigenvalue, and the y-axis represents the eigenvalue value. The figure demonstrates that the eigenvalues decay rapidly, supporting the use of low-rank approximations of the GGN matrix. The standard deviation is shown for each eigenvalue across 5 different random seeds, indicating the stability of the observed decay.
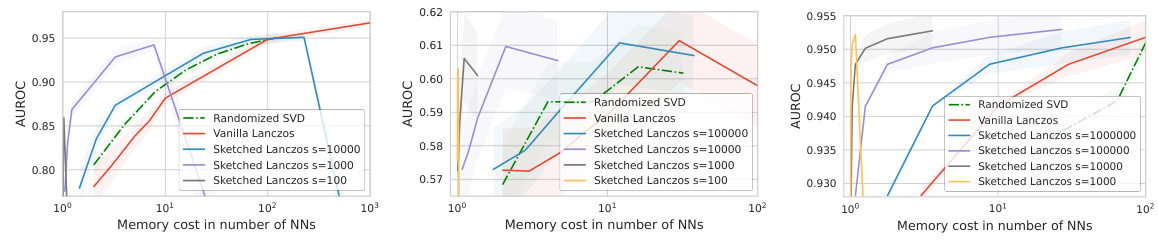
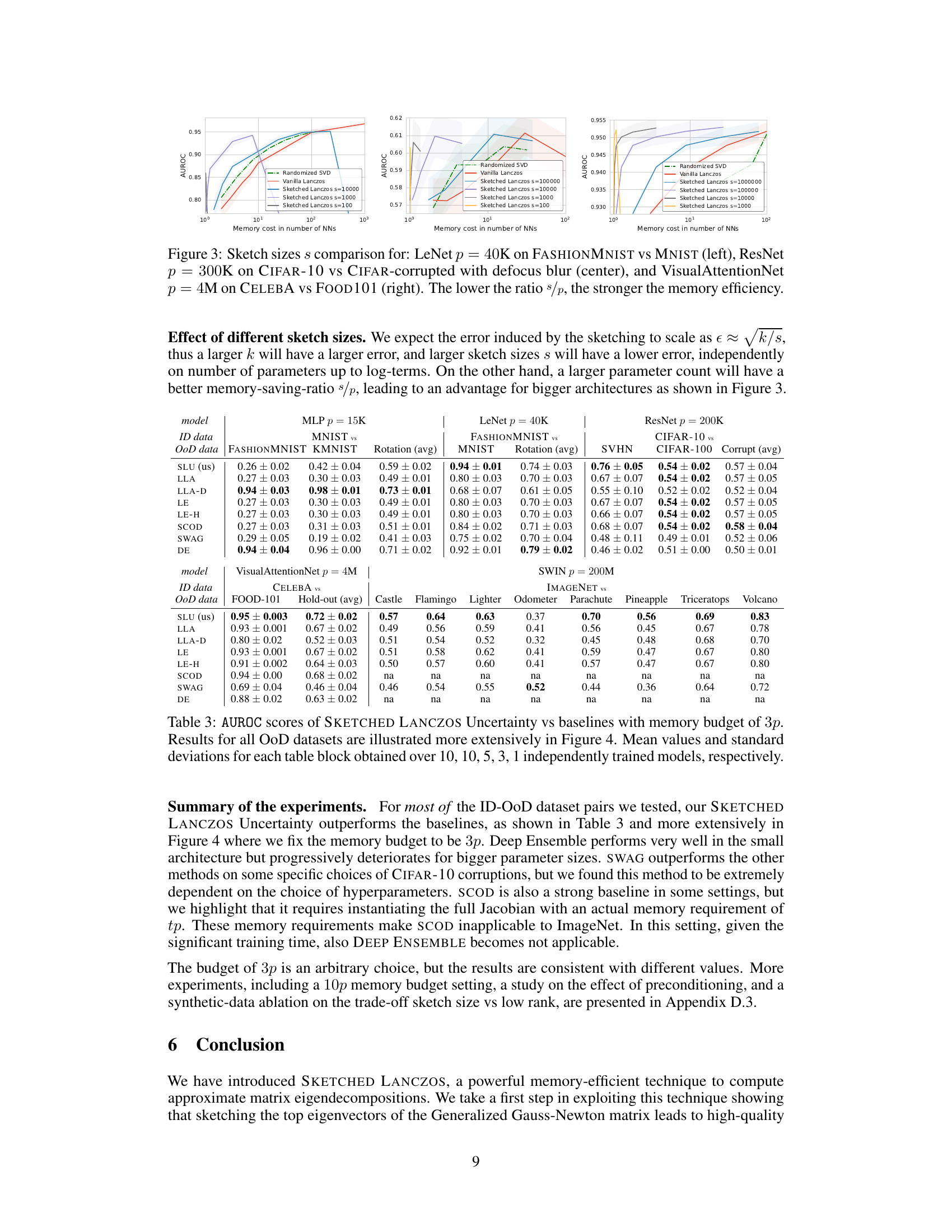
This figure compares the performance of the Sketched Lanczos algorithm with different sketch sizes (s) on three different model architectures (LeNet, ResNet, VisualAttentionNet) and datasets. It demonstrates how the memory efficiency of Sketched Lanczos improves as the ratio of sketch size to the number of model parameters (s/p) decreases. Each subfigure displays the AUROC (Area Under the Receiver Operating Characteristic curve) for out-of-distribution (OoD) detection as a function of memory cost (in the number of neural networks).
This figure compares the performance of SKETCHED LANCZOS with different sketch sizes (s) for three different model architectures and datasets. The x-axis represents the memory cost in the number of neural networks, and the y-axis shows the AUROC (Area Under the Receiver Operating Characteristic curve), a measure of the model’s ability to distinguish between in-distribution and out-of-distribution samples. The figure demonstrates that smaller sketch sizes lead to more memory-efficient uncertainty quantification. The lower the ratio of sketch size (s) to the number of parameters (p), the better the memory efficiency, meaning less memory is used to achieve the same uncertainty prediction quality.
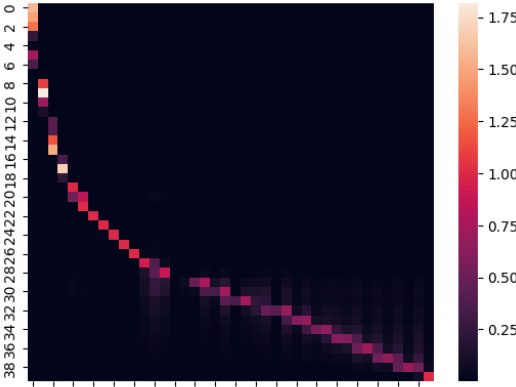
This figure shows the comparison between eigenvectors obtained from hi-memory Lanczos and low-memory Lanczos on the Generalized Gauss-Newton (GGN) matrix of a LeNet model trained on MNIST. The plot visualizes the dot product between eigenvectors from each method, revealing that several low-memory Lanczos eigenvectors correspond to the same high-memory Lanczos eigenvector. This observation supports the idea that low-memory Lanczos, despite its lack of strict orthogonality, provides a good approximation of the top eigenvectors.
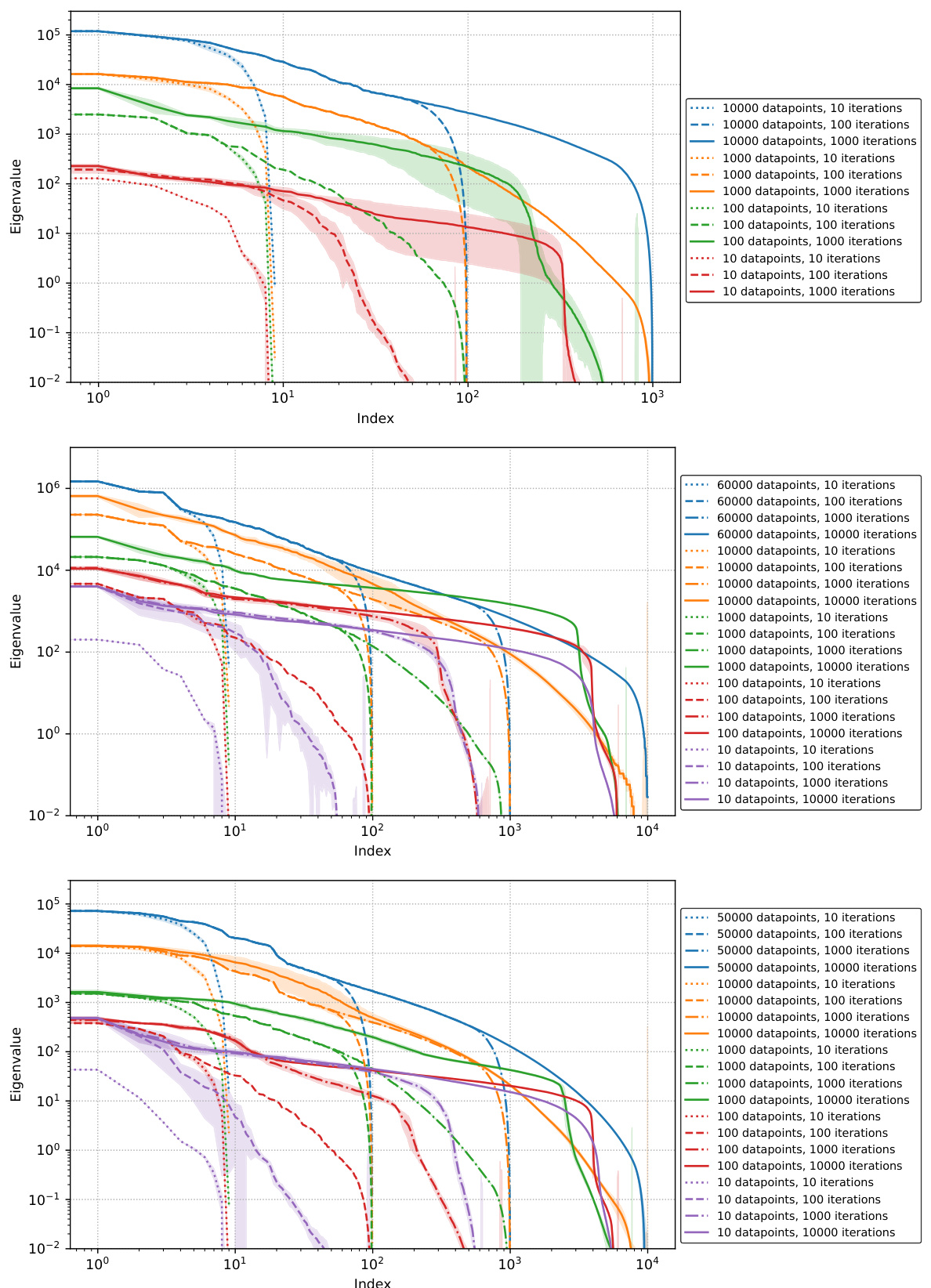
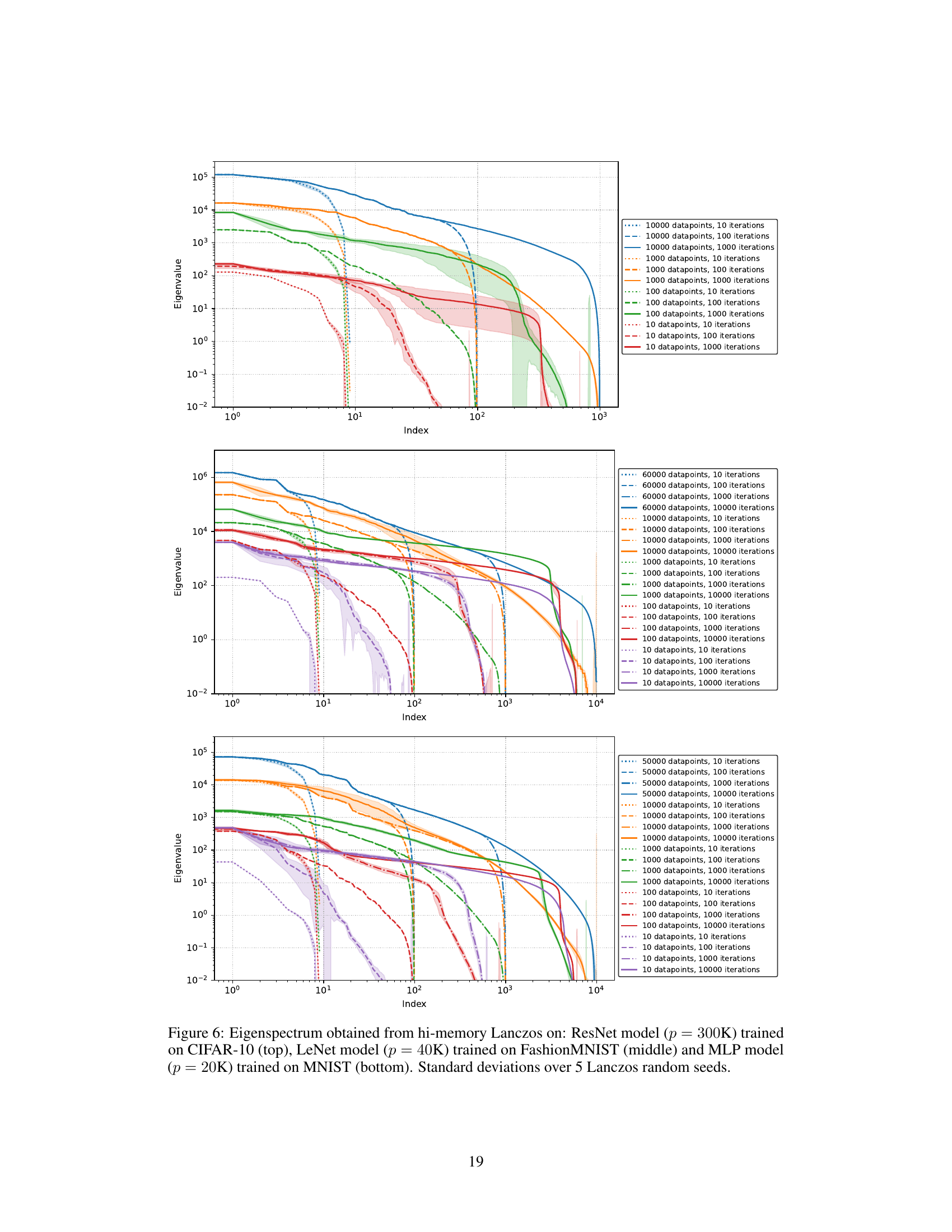
This figure shows the eigenspectrum obtained from the hi-memory Lanczos algorithm for three different neural network models trained on different datasets. The top panel shows results for a ResNet model trained on CIFAR-10, the middle panel for a LeNet model trained on FashionMNIST, and the bottom panel for an MLP model trained on MNIST. The plot displays the eigenvalues (y-axis) against their index (x-axis), illustrating the distribution of eigenvalues. Standard deviations are shown across five different random initializations of the Lanczos algorithm, indicating variability in the results. The rapid decay of eigenvalues suggests that the GGN matrix can be well approximated by a low-rank matrix.

This figure compares the performance of the Sketched Lanczos algorithm with different sketch sizes (s) across three different model architectures (LeNet, ResNet, and VisualAttentionNet) and datasets. It shows that reducing the ratio of sketch size to the number of parameters (s/p) improves the memory efficiency of the algorithm while maintaining reasonable performance. The lower the s/p ratio, the better the memory efficiency.
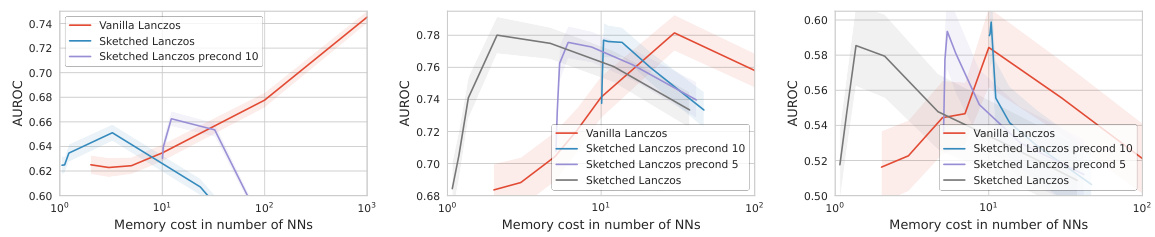
This figure compares the performance of vanilla Lanczos, sketched Lanczos, and sketched Lanczos with preconditioning on three different datasets. The x-axis represents the memory cost in the number of neural networks. The y-axis represents the AUROC (Area Under the Receiver Operating Characteristic curve), a measure of the accuracy of out-of-distribution detection. The figure demonstrates that preconditioning, a technique that improves the numerical stability of the Lanczos algorithm, significantly enhances the memory efficiency of sketched Lanczos, allowing for higher-rank approximations within the same memory budget.

This figure compares the performance of SKETCHED LANCZOS with different sketch sizes (s) for three different neural network architectures (LeNet, ResNet, VisualAttentionNet) on out-of-distribution (OoD) detection tasks. The x-axis represents the memory cost in the number of neural networks, and the y-axis represents the AUROC score. The results demonstrate that smaller s/p ratios lead to greater memory efficiency. Each plot shows the performance with varying sketch sizes and highlights the trade-off between accuracy and memory usage.
More on tables

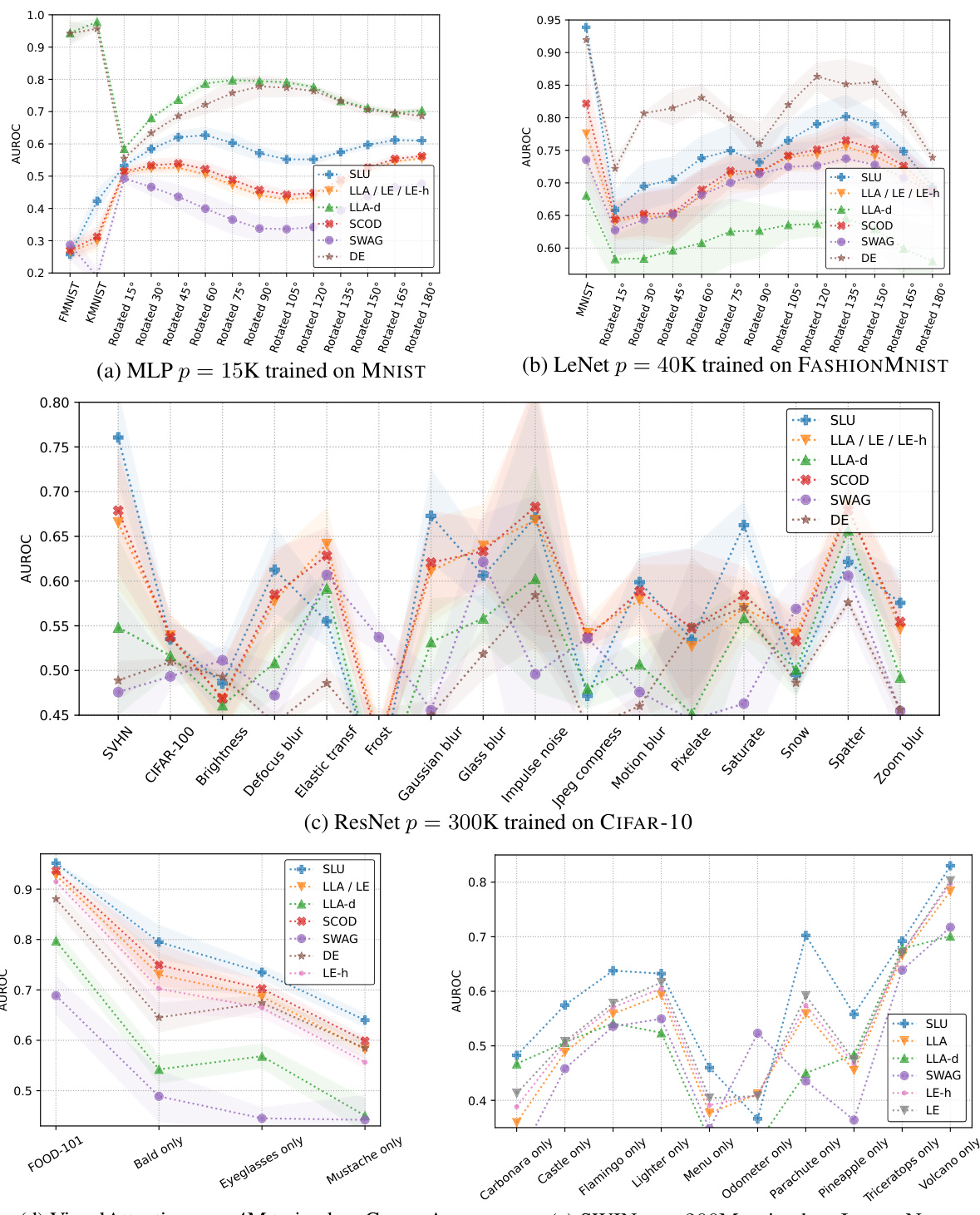
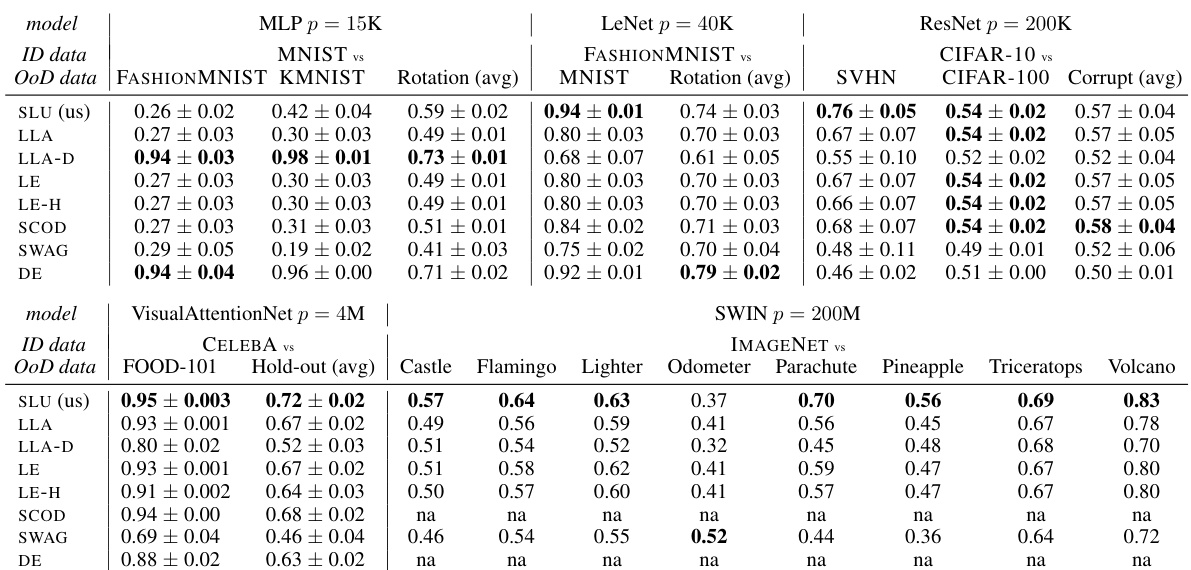
This table presents the results of out-of-distribution (OOD) detection experiments comparing the proposed Sketched Lanczos Uncertainty (SLU) method to other baselines. The AUROC (Area Under the Receiver Operating Characteristic curve) scores are reported for various model architectures and datasets with a memory budget of 3 times the number of parameters (3p). The table includes average AUROC scores and standard deviations across multiple independently trained models.
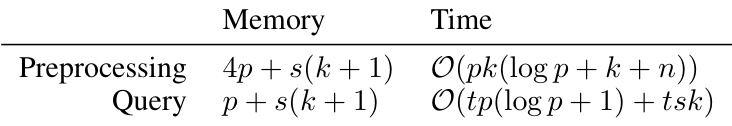
This table summarizes the memory and time complexities of the proposed SKETCHED LANCZOS algorithm. It breaks down the computational cost into preprocessing (offline) and query (online) phases. The notation uses standard big O notation to express the scaling of computation with respect to the number of parameters (p), dataset size (n), output dimensionality (t), rank approximation (k), and sketch size (s).
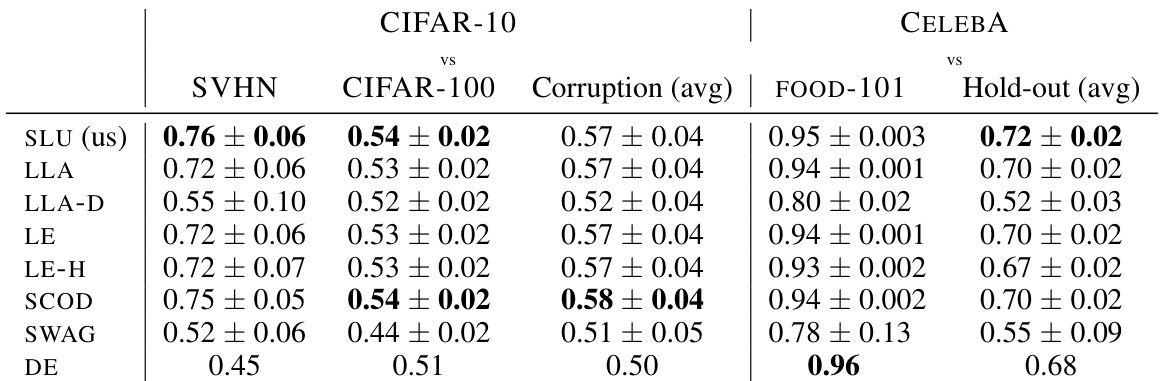
This table presents the Area Under the Receiver Operating Characteristic (AUROC) scores for out-of-distribution (OoD) detection. It compares the performance of the proposed Sketched Lanczos Uncertainty (SLU) method against several baseline methods across various models and datasets. The memory budget is fixed at 3p (where p is the number of parameters). The table shows the AUROC scores for different in-distribution (ID) vs out-of-distribution (OoD) dataset pairs and includes mean and standard deviation for each entry, calculated from multiple independent runs of each experiment.

This table presents the Area Under the Receiver Operating Characteristic (AUROC) scores for out-of-distribution (OOD) detection. It compares the performance of the proposed Sketched Lanczos Uncertainty (SLU) method against several baseline methods. The results are shown for various model architectures (MLP, LeNet, ResNet, VisualAttentionNet, Swin) and datasets, each with a limited memory budget of 3p (three times the number of parameters). The table provides mean AUROC scores and standard deviations across multiple independently trained models for each experiment.
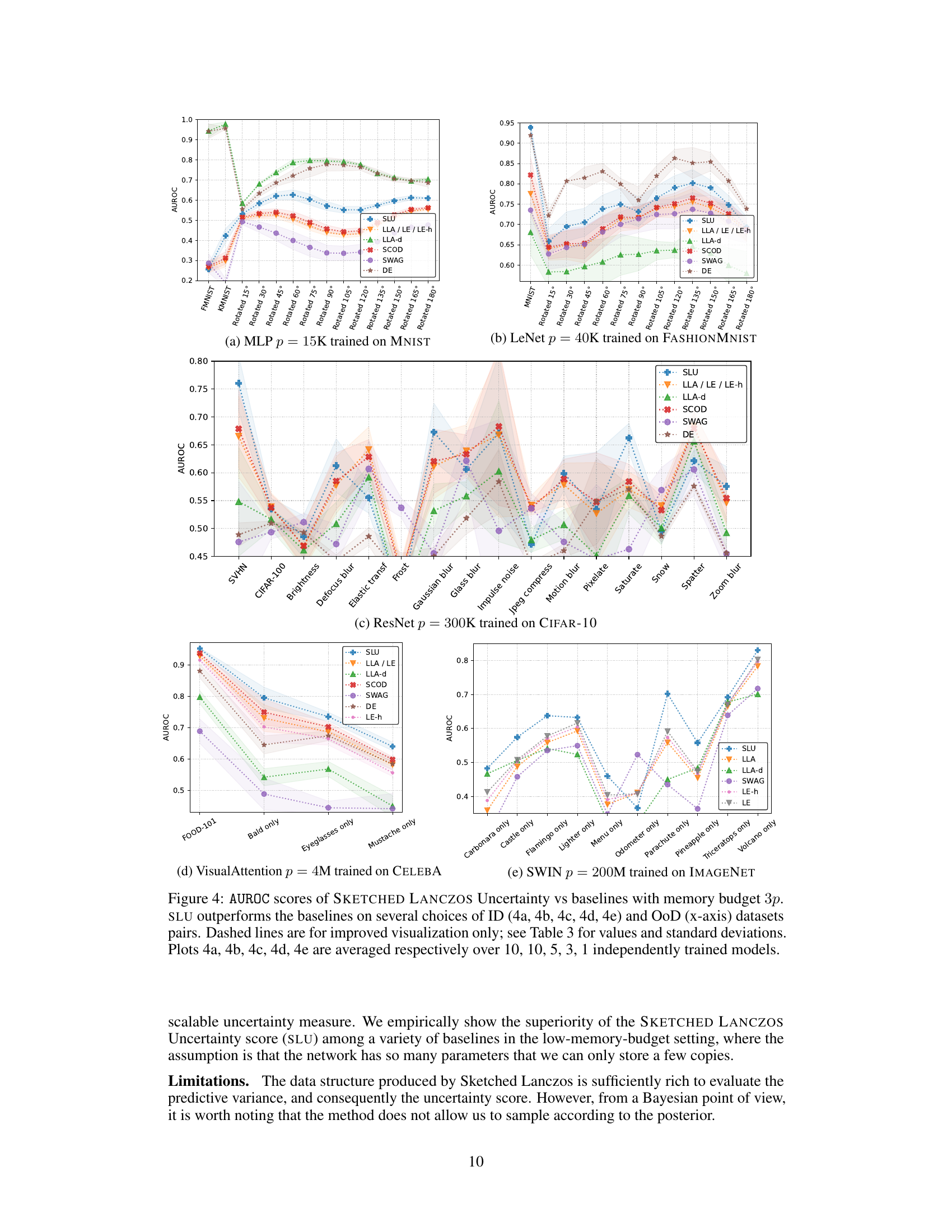
This table presents the Area Under the Receiver Operating Characteristic (AUROC) scores for out-of-distribution (OoD) detection. It compares the performance of the proposed Sketched Lanczos Uncertainty (SLU) method against several baseline methods (Linearized Laplace Approximation, Local Ensemble, Sketching Curvature for OoD Detection, Stochastic Weight Averaging Gaussian, Deep Ensemble) across various models and datasets. The memory budget is fixed at 3p (three times the number of parameters). The number of independently trained models used for averaging varies across datasets (10, 10, 5, 3, 1). Figure 4 provides a more detailed visualization of these results.
Full paper#