Temporal Graph Neural Tangent Kernel with Graphon-Guaranteed

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in temporal graph learning because it introduces Temp-G³NTK, a novel method with strong theoretical guarantees and excellent empirical performance. It addresses the limitations of existing approaches by handling temporal evolution effectively and efficiently, thus opening new avenues for various graph-related tasks and potentially impacting large-scale applications.

Visual Insights

#

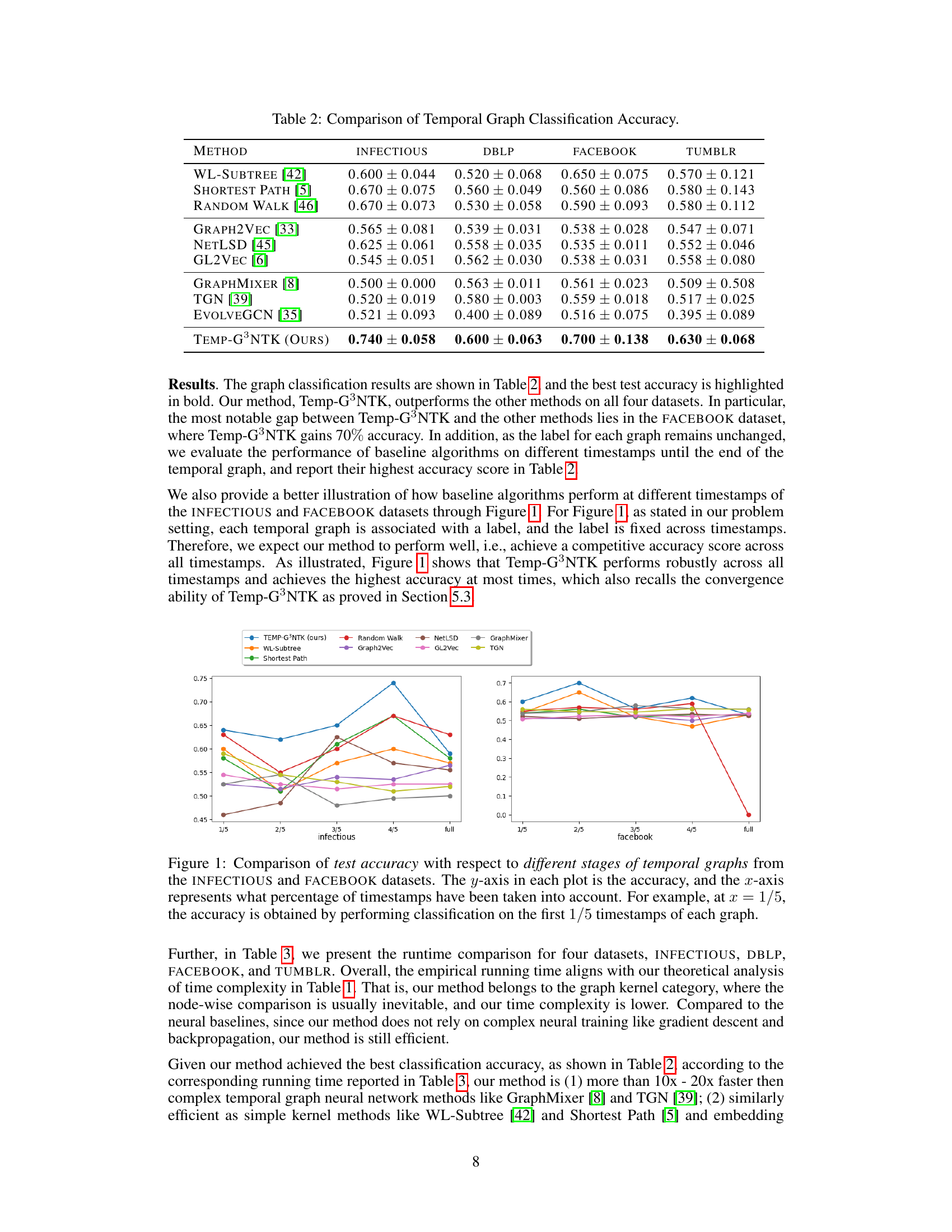
This figure shows the test accuracy of different temporal graph classification methods across various stages of temporal graph data from the INFECTIOUS and FACEBOOK datasets. The x-axis represents the fraction of timestamps used (1/5, 2/5, 3/5, 4/5, full), showing how the accuracy changes as more temporal information is incorporated. The y-axis represents the classification accuracy. The figure allows comparison of Temp-G³NTK against various baseline methods.

This table compares the runtime complexity of different graph kernel and graph neural network methods for computing pairwise similarity between n temporal graphs. The complexity is analyzed in terms of several key factors, such as the number of nodes (|V|), number of edges (|E|), number of iterations in WL-subtree (h), maximum degree (D), number of eigenvalues (k), number of BLOCK operations (L), and number of training epochs (B). It shows that the Temp-G³NTK method, proposed in the paper, has a lower time complexity than most graph neural network methods.

In-depth insights

#

Temp-GNTK Kernel

#

The conceptualization of a ‘Temp-GNTK Kernel’ presents a compelling advancement in graph neural network research. By integrating the strengths of Graph Neural Tangent Kernels (GNTKs) with the capability to handle temporal graph data, this approach offers a powerful method for analyzing dynamic relationships. The name itself suggests a fusion of concepts: the established GNTK framework providing interpretability and mathematical rigor, extended to the temporal domain to capture the evolving nature of real-world networks. A key advantage would be the simplification of the graph representation learning process, moving away from complex neural network architectures and potentially computationally expensive training towards a more efficient kernel-based methodology. Furthermore, theoretical guarantees on the performance, such as convergence and error bounds, would add significant value and trustworthiness. Graphon-guaranteed aspects, as the paper suggests, indicate potential scalability and robustness, especially important when dealing with large-scale temporal graphs. Overall, the proposed Temp-GNTK kernel offers a promising approach to unlock insights from dynamic networks while maintaining the desirable properties of GNTKs.

Theoretical Guarantees

#

A theoretical guarantees section in a research paper would rigorously establish the soundness and reliability of the proposed methods. This would likely involve proving convergence theorems, demonstrating error bounds, or showing generalization capabilities. For machine learning models, this might mean showing the model will converge to a solution, providing guarantees on the model’s performance on unseen data, or establishing bounds on the generalization error. Such guarantees are crucial for building trust and confidence in the new method and are often a significant contribution of the work. The strength of these theoretical guarantees will depend on the complexity of the method and the assumptions made, with stronger guarantees usually requiring more restrictive assumptions. Ideally, the guarantees should be tight, meaning they accurately reflect the model’s performance, and practical, meaning the assumptions are realistic for real-world applications.

Temporal Graphon Limit

#

The concept of a ‘Temporal Graphon Limit’ is a fascinating extension of graphon theory into the dynamic realm. It suggests investigating how the structure of a time-evolving graph converges as both the number of nodes and the observation period increase. This involves considering not only the static properties of the graph at any given time but also the temporal dependencies between snapshots. A key challenge would be defining a suitable notion of convergence, as temporal graphs don’t naturally lend themselves to the same limit processes as static graphs. The limit object, if one exists, might be a function describing the probability distribution of the graph’s structure and feature evolution over time. This would provide a powerful tool for analyzing large-scale dynamic systems and performing efficient inference. The theoretical analysis would require sophisticated mathematical techniques from probability theory and graph limit theory. Applications could range from modeling social networks to understanding biological processes, capturing the evolutionary trends of relationships and interactions and inferring fundamental patterns of dynamic behavior that wouldn’t be apparent from analyzing individual snapshots.

Node-Level Extension

#

A ‘Node-Level Extension’ in a graph neural network (GNN) research paper would likely detail how the model’s capabilities extend beyond graph-level classification to encompass node-level tasks. This could involve adapting the model architecture to predict node attributes or perform node classification directly. A key consideration would be how the learned graph representations are utilized to make predictions at the node level. This might involve attention mechanisms focusing on node neighborhoods, or employing a method like graph pooling to aggregate local information before prediction. The paper might also present experimental results on node-level tasks, comparing the proposed method’s performance against relevant baselines. Another important aspect could be the discussion of computational efficiency, especially when dealing with large graphs where node-level prediction can be computationally expensive. Furthermore, the extension could introduce new theoretical analysis for the node-level setting, such as generalization bounds, convergence properties or a detailed explanation of how node-level prediction leverages the graph-level learned information. The discussion of the theoretical properties could be crucial in proving the efficacy and robustness of the node-level extension.

Scalability and Efficiency

#

A crucial aspect of any machine learning model is its scalability and efficiency. Scalability refers to the model’s ability to handle increasingly large datasets and complex tasks without significant performance degradation. Efficiency focuses on the computational resources required for training and inference, aiming for minimal time and energy consumption. In the context of graph neural networks, scalability often becomes challenging due to the complex relationships and structural characteristics inherent to graph data. Efficient algorithms and architectures are crucial for practical deployment of such models, particularly when dealing with massive datasets. The paper likely addresses these challenges by proposing novel methods that improve the model’s ability to manage large graphs and optimize computational processes. This might involve techniques such as approximation algorithms, distributed computing, optimized data structures, or hardware acceleration. A detailed analysis of runtime complexity and empirical evaluations would be essential to demonstrate improvements in both scalability and efficiency. The discussion should highlight the model’s performance on large-scale benchmarks and compare its computational cost to existing approaches.

More visual insights

#

More on figures

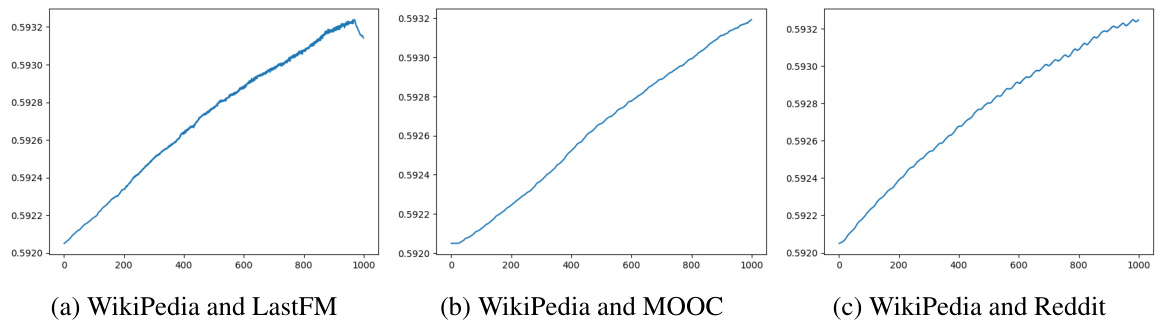
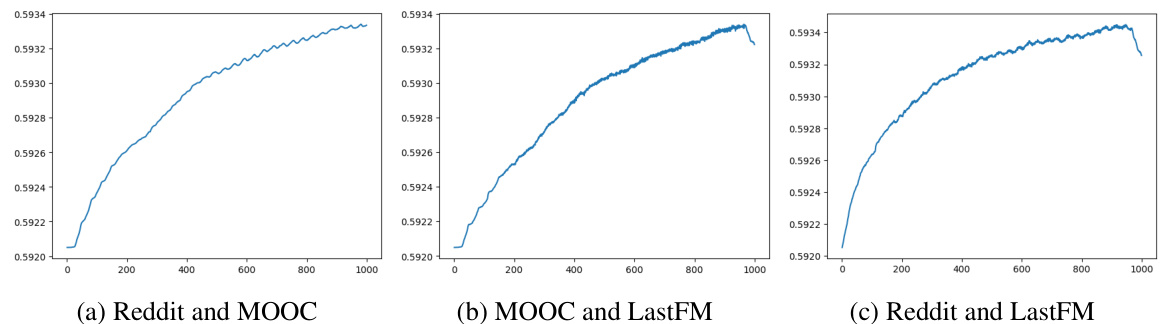
This figure displays the Temp-G³NTK similarity values over time for various pairs of temporal graphs. The x-axis represents the timestamp (rescaled to 0-1000 for better comparison across graphs with varying time spans), and the y-axis shows the Temp-G³NTK value. Each subplot shows a different pair of graphs, illustrating how the similarity changes over time. This visualization helps demonstrate the convergence property of Temp-G³NTK.

This figure compares the classification accuracy of different models on the INFECTIOUS and FACEBOOK datasets at various stages of the temporal graphs. The x-axis shows the proportion of timestamps used for classification (e.g., 1/5 means only the first 20% of timestamps were used), and the y-axis represents the achieved accuracy. The figure visually demonstrates how the accuracy changes as more temporal information is included in the classification process.

The figure shows a comparison of the test accuracy of various temporal graph classification methods across different stages of temporal graphs from the INFECTIOUS and FACEBOOK datasets. The x-axis represents the proportion of timestamps used for classification (e.g., 1/5 means only the first 20% of timestamps were used), and the y-axis represents the achieved accuracy. It visually demonstrates the performance of Temp-G³NTK and other methods as more temporal information becomes available.

More on tables

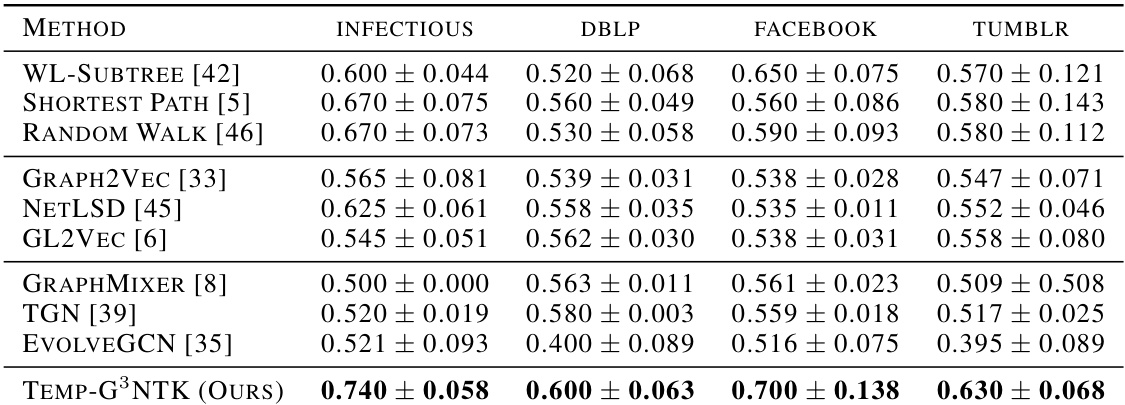
This table presents the classification accuracy results for different methods on four datasets: Infectious, DBLP, Facebook, and Tumblr. The accuracy is reported as mean ± standard deviation. Temp-G³NTK achieves the highest accuracy on all datasets, indicating its superior performance in temporal graph classification.

This table presents the runtime comparison of different graph classification methods across four datasets: Infectious, DBLP, Facebook, and Tumblr. The runtime is measured in seconds for each method. It shows the computational efficiency of Temp-G³NTK compared to other methods, particularly highlighting its speed advantage over neural network-based approaches.

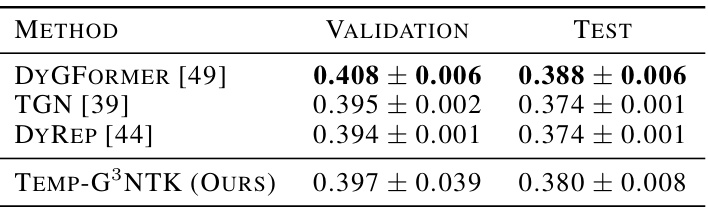
This table presents the results of node property prediction experiments on the tgbn-trade dataset. It compares the performance of Temp-G³NTK against three baseline methods (DyGFormer, TGN, and DyRep) using the NDCG score. The results are shown for both validation and test sets, demonstrating Temp-G³NTK’s competitive performance in this task.

This table presents the results of an ablation study conducted to investigate the impact of different time encoding functions on the classification accuracy of the Temp-G³NTK model. The study used the INFECTIOUS dataset and compared four different time encoding methods: Absolute Difference, Absolute Difference Encoding, Relative Difference, and the proposed Temp-G³NTK with Relative Difference Encoding. The table shows that the Temp-G³NTK model with relative difference encoding achieved the highest accuracy.

This table shows the result of an ablation study on the INFECTIOUS dataset to analyze how different numbers of recent neighbors affect the performance of the Temp-G³NTK model. The study varies the number of recent neighbors considered for aggregation from 5 to 25, and also includes a result using all neighbors. The accuracy for each configuration is reported, showing that using all neighbors yields the highest accuracy.

This table presents the statistics of four small temporal graph datasets used in the paper’s graph-level experiments. For each dataset, the number of graphs, number of classes, average number of nodes, and average number of edges are provided. This information is crucial for understanding the scale and characteristics of the data used in the experiments and for comparing the results across different datasets.

This table presents the statistics of four large temporal graph datasets used in the paper’s experiments. For each dataset, it lists the number of users, the number of items, and the total number of interactions.

Full paper

#