↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Semi-supervised graph domain adaptation (SGDA) aims to label unlabeled target graph nodes using knowledge from a source graph with limited labels. Existing methods primarily focus on feature alignment, neglecting the valuable structural information within graphs. This leads to suboptimal performance, especially in the presence of domain discrepancies and limited labeled data.
The proposed TFGDA framework tackles these challenges by incorporating both feature and structural alignment. It uses a novel Subgraph Topological Structure Alignment (STSA) strategy to encode topological information in latent space and improve transfer learning. Further, a Sphere-guided Domain Alignment (SDA) method ensures stable alignment, while a Robustness-guided Node Clustering (RNC) strategy addresses overfitting. Extensive experiments demonstrate TFGDA’s superiority over existing SGDA methods across various benchmarks.
Key Takeaways#
Why does it matter?#
This paper is important because it presents TFGDA, a novel framework for semi-supervised graph domain adaptation that significantly outperforms state-of-the-art methods. It addresses the limitations of existing approaches by effectively leveraging both topological structure and feature alignment, opening avenues for more robust and generalizable graph transfer learning models. This is particularly relevant given the increasing use of graph data across various domains.
Visual Insights#
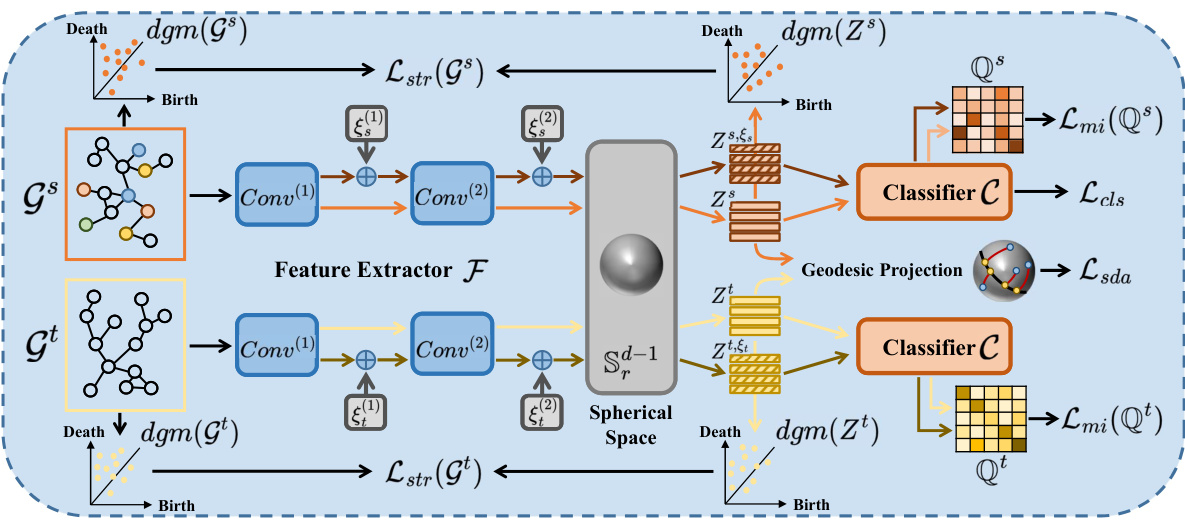
This figure illustrates the TFGDA model’s architecture, highlighting its three main components: STSA for structure alignment, SDA for domain alignment, and RNC for robust clustering. The model processes both source and target graphs, encoding topological structure information and aligning feature distributions in a spherical space to mitigate domain discrepancy and overfitting. The RNC component enhances model robustness by guiding discriminative clustering of unlabeled nodes.

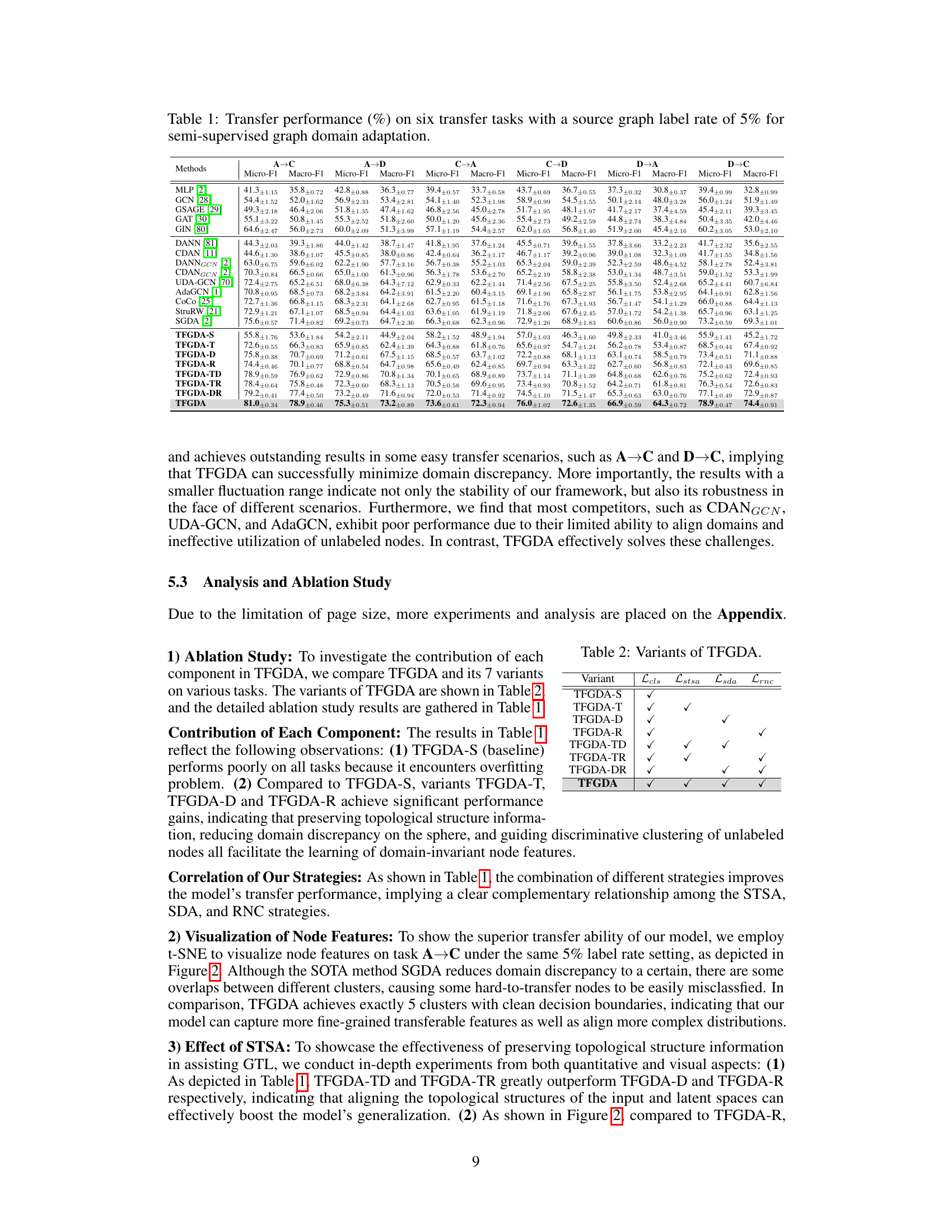
This table presents the performance of various methods on six different semi-supervised graph domain adaptation tasks. Each task involves transferring knowledge from a source graph to a target graph, where only 5% of the source graph’s nodes are labeled. The performance is measured using Micro-F1 and Macro-F1 scores, which evaluate the model’s ability to correctly classify nodes in the target graph. The results show a comparison of TFGDA and its variants against several state-of-the-art (SOTA) methods for semi-supervised graph domain adaptation and graph semi-supervised learning.
In-depth insights#
SGDA Framework#
A hypothetical Semi-Supervised Graph Domain Adaptation (SGDA) framework would aim to bridge the gap between limited labeled source data and abundant unlabeled target data. Effective feature alignment is crucial, potentially leveraging techniques like adversarial training or optimal transport to minimize domain discrepancies. Structure alignment is equally important, recognizing that graphs encode relationships and that preserving topological structure during adaptation can significantly improve generalizability. Robust clustering methods are essential for handling the scarcity of labeled data and to guide the discriminative learning of unlabeled target nodes. A robust SGDA framework would likely integrate these components—feature and structure alignment, robust clustering—into a unified model, perhaps using a graph neural network architecture. Addressing overfitting in the source domain is paramount, requiring techniques to prevent the model from memorizing the limited labeled samples. Finally, the framework’s success hinges on selecting appropriate metrics to evaluate the performance on the target domain, given the absence of extensive ground truth labels.
Topology Encoding#
Topology encoding in graph neural networks aims to capture and utilize the structural information inherent in graph data. Rather than relying solely on node features, topology encoding methods focus on the relationships between nodes, leveraging concepts from topological data analysis (TDA) such as persistent homology. These techniques often involve constructing simplicial complexes (e.g., Vietoris-Rips complexes) from the graph’s adjacency matrix and then computing persistent homology to extract topological features that represent the graph’s shape and connectivity at multiple scales. These topological features are then integrated into the GNN architecture, often by concatenating them with node features or using them as input to separate layers. Robustness is a key consideration, as topological features can be sensitive to noise and perturbations in the input graph. Therefore, techniques for handling noise and ensuring stability are crucial for effective topology encoding. Furthermore, computational efficiency is a major challenge, as TDA computations can be computationally expensive, especially for large graphs. The effectiveness of topology encoding also depends on the specific application and the type of graph data being analyzed. Some applications may benefit more than others from incorporating topological features into the GNN model.
Robust Clustering#
Robust clustering, in the context of semi-supervised graph domain adaptation, addresses the challenge of reliable node classification with limited labeled data. The core idea is to develop a clustering approach that is insensitive to noise and outliers, common in real-world datasets and particularly prevalent when dealing with a scarcity of labeled examples. This robustness is crucial because inaccurate clustering can lead to the propagation of errors during the transfer learning process from a source graph to a target graph. Effective robust clustering techniques should leverage available structural information within the graph to guide the clustering process, thereby improving the overall accuracy and generalization ability of the model. Furthermore, a robust clustering strategy should be computationally efficient to handle large-scale graphs and integrate seamlessly within the larger domain adaptation framework. The goal is not merely to group similar nodes together, but to ensure that the resulting clusters accurately reflect the underlying data distribution and facilitate effective knowledge transfer between domains.
Sphere Alignment#
Sphere alignment, in the context of graph domain adaptation, offers a novel approach to aligning feature distributions. By mapping node features onto a hypersphere, it leverages the sphere’s unique geometric properties to mitigate domain discrepancies. This approach is particularly attractive because it addresses limitations of traditional methods that often rely on adversarial training, which can be unstable and lead to the loss of discriminative information. The use of geodesic distances on the sphere provides a more stable and robust measure of feature similarity, improving transferability and the overall performance. The spherical representation naturally handles the non-Euclidean nature of graph data, making it more suitable than Euclidean-based methods. Furthermore, the strategy is potentially computationally efficient, especially for high-dimensional data. Mapping to a sphere creates a more stable framework, effectively reducing the negative impacts of adversarial training. A key advantage is the inherent stability and robustness, enabling the model to better handle variations in feature distributions, leading to more accurate and reliable domain adaptation.
Future Works#
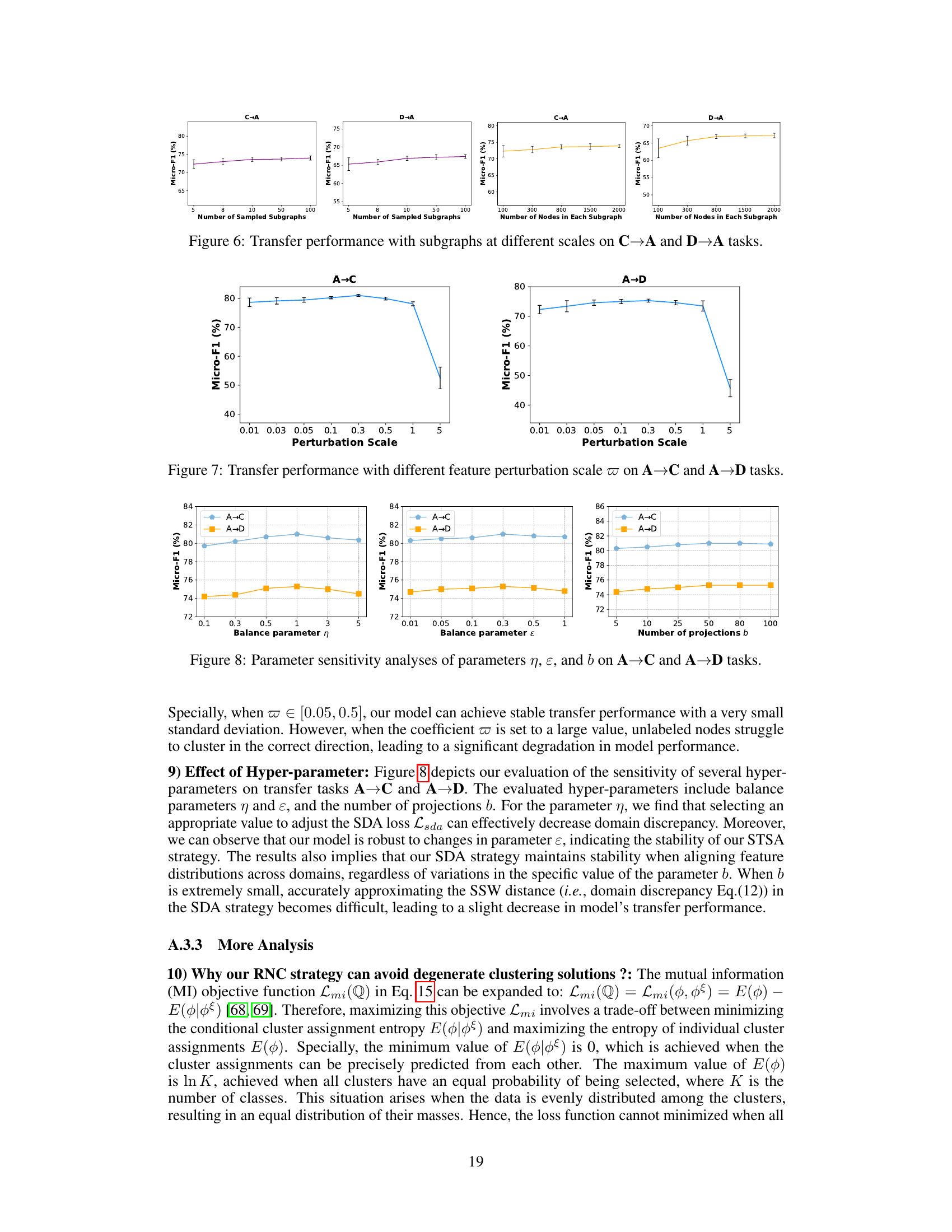
Future work could explore several promising avenues. Extending TFGDA to handle dynamic graphs is crucial, as many real-world graphs evolve over time. This would involve adapting the model to incorporate temporal dependencies and changes in graph structure. Investigating different subgraph sampling techniques could further improve STSA’s efficiency and robustness, potentially exploring strategies that prioritize informative subgraphs based on centrality or other relevant node properties. Analyzing the impact of different distance metrics used in the SSW calculation would also help optimize the SDA strategy. Furthermore, applying TFGDA to diverse graph types, such as heterogeneous graphs or attributed graphs, would demonstrate its generalizability and broaden its applicability. Finally, a more in-depth theoretical analysis of TFGDA’s convergence properties and its ability to generalize across various domains is warranted, providing a more rigorous foundation for its effectiveness.
More visual insights#
More on figures

This figure visualizes the representations learned by SGDA, TFGDA, and two of its variants using t-SNE on the A→C transfer task with a 5% label rate. The top row shows the visualization of different categories, while the bottom row visualizes the alignment between source and target domains. The figure demonstrates how TFGDA improves category separation and domain alignment compared to SGDA.

This figure actually contains two sub-figures. The left one shows the training curves of different variants of the proposed model (TFGDA) and some baseline models (SGDA, TFGDA-S, TFGDA-R, etc.) on two tasks (A→C and A→D). The right one shows the performance of different models with different label rates on the same two tasks. The figures indicate that the proposed model converges more smoothly and quickly, and achieves better performance than baselines under different label rates.
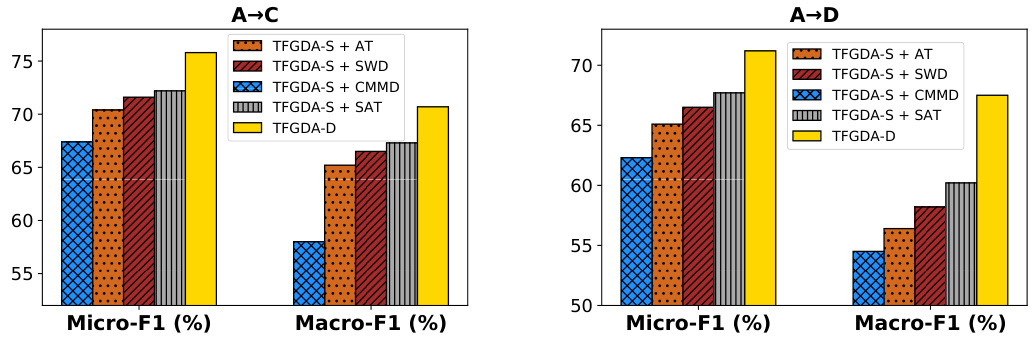
The bar chart compares the performance of TFGDA with different domain alignment strategies on two transfer tasks: A→C and A→D. The baseline model is TFGDA-S, and various alignment strategies such as AT, SWD, CMMD, and SAT are added to TFGDA-S. TFGDA-D, which uses the SDA strategy, serves as a comparison point. The chart shows that TFGDA-D generally achieves the best performance compared to the baseline and other methods in both Micro-F1 and Macro-F1 scores. This suggests that the SDA strategy is effective for aligning feature distributions.

This figure visualizes the t-SNE representations of node features learned by SGDA, TFGDA, and two variants of TFGDA on the A→C task using a 5% label rate. The visualization helps understand how different models perform domain adaptation. Subfigures (a-d) show the clustering of nodes into different categories (colors), while subfigures (e-h) illustrate the alignment of source and target domains (red and blue, respectively). The comparison aims to highlight TFGDA’s improved ability to separate categories and align domains.
This figure visualizes the t-SNE representations learned by SGDA, TFGDA, and two variants of TFGDA on the A→C transfer task with a 5% label rate. The visualization shows the separation of different classes (a-d) and the alignment of source and target domains (e-h). The results demonstrate that TFGDA improves the separation of classes and alignment of domains compared to SGDA.
This figure shows the overall architecture of the TFGDA model, highlighting the three main components: Subgraph Topological Structure Alignment (STSA), Sphere-guided Domain Alignment (SDA), and Robustness-guided Node Clustering (RNC). STSA encodes the topological structure of the graphs into a spherical space to improve generalization, while SDA aligns feature distributions across domains within this space. RNC addresses overfitting by guiding discriminative clustering of unlabeled nodes.
More on tables
This table presents the performance comparison of different methods on six semi-supervised graph domain adaptation tasks. The performance is evaluated using Micro-F1 and Macro-F1 scores. The source graph has a label rate of 5%. The methods being compared include several state-of-the-art (SOTA) graph semi-supervised learning and graph domain adaptation methods.

This table presents the key statistics for three real-world graph datasets used in the paper: ACMv9 (A), Citationv1 (C), and DBLPv7 (D). For each graph, it provides the number of nodes, the number of edges, the number of attributes per node, the average node degree, and the label proportion (percentage of nodes labeled for each of the five classes). These statistics highlight the size and characteristics of the datasets, which are crucial for understanding the experimental setup and results.

This table presents the performance of various methods on six graph semi-supervised domain adaptation tasks. Each task involves transferring knowledge from a labeled source graph to an unlabeled target graph, with only 5% of nodes in the source graph being labeled. The performance is measured using Micro-F1 and Macro-F1 scores, and the results demonstrate the superiority of the proposed TFGDA method compared to several state-of-the-art methods.
Full paper#