↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Image restoration is a crucial task in computer vision, but existing methods often require multiple steps or lack generality. This leads to limitations in real-time applications and restricts applicability across various image degradation types. Many methods also depend on pre-trained models, impacting their independence and performance.
This paper introduces IR-CM, a novel image restoration method based on a consistency model trained via a new linear-nonlinear decoupling strategy. This allows for fast, few-step, or even one-step inference. By incorporating an origin-guided loss, the method avoids trivial solutions and achieves state-of-the-art performance on various tasks such as deraining, denoising, deblurring, and low-light enhancement, surpassing existing methods without needing pre-trained checkpoints.
Key Takeaways#
Why does it matter?#
This paper is significant because it presents IR-CM, a novel and fast image restoration method that achieves state-of-the-art performance with only one or two steps. Its universality and efficiency are crucial for real-time applications, such as autonomous driving and robotics. The introduction of linear-nonlinear decoupling training strategy is also important as it enhances the training’s effectiveness and surpasses the consistency distillation method. This work opens up new avenues for research in fast and generalized image restoration.
Visual Insights#

This figure illustrates the two-stage training strategy used in the IR-CM model. The first stage (linear fitting) simplifies the process by adding noise to the low-quality image, allowing for efficient consistency training. The second stage (nonlinear fitting) starts with a high-quality image and gradually degrades it, again applying consistency training on the intermediate steps. This two-stage approach enhances the training and inference performance.
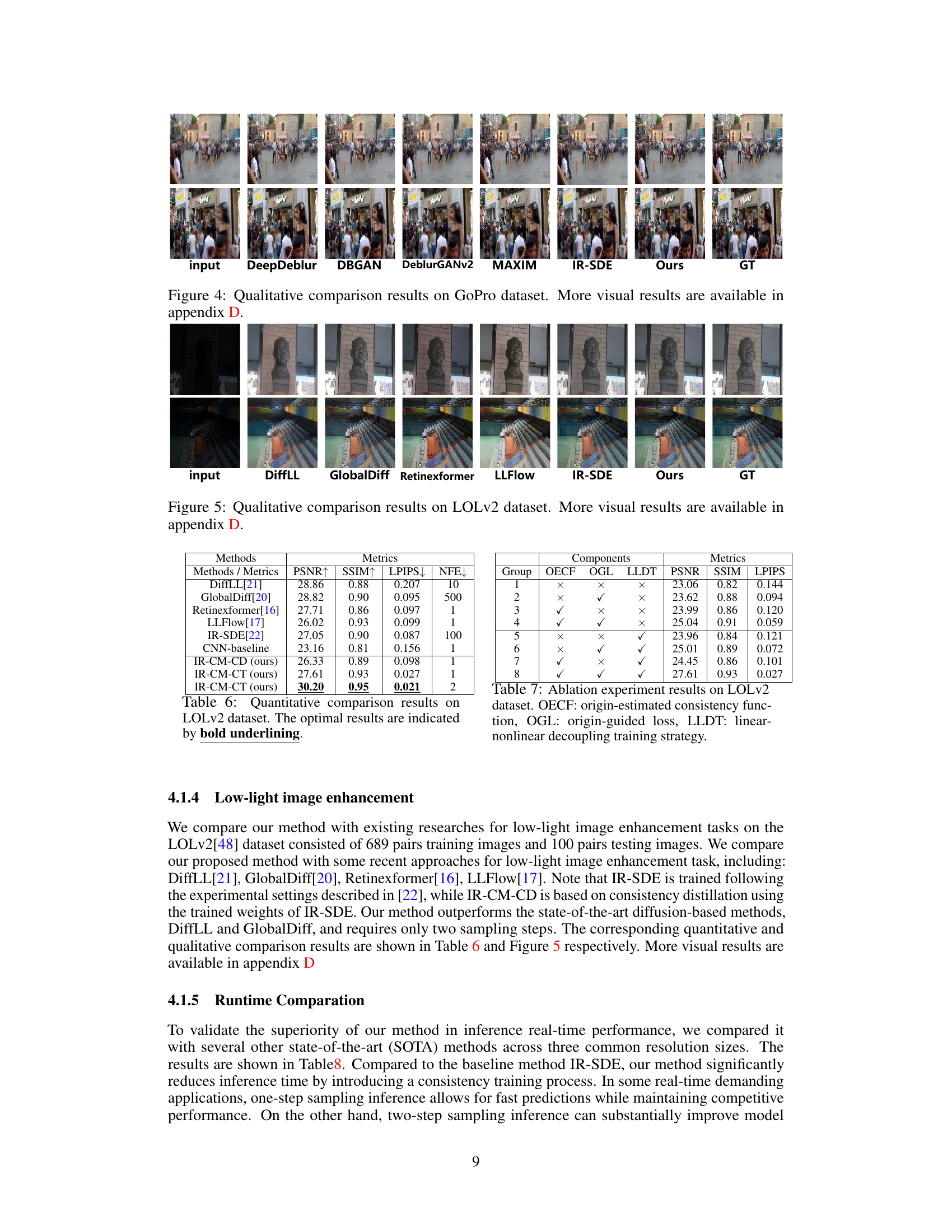
This table presents a quantitative comparison of the proposed IR-CM method with several state-of-the-art image deraining methods on the R100H dataset. The metrics used for comparison are PSNR (Peak Signal-to-Noise Ratio), SSIM (Structural Similarity Index), LPIPS (Learned Perceptual Image Patch Similarity), and NFE (Number of Function Evaluations). Higher PSNR and SSIM values indicate better image quality, while a lower LPIPS value indicates better perceptual similarity to the ground truth. NFE represents the number of inference steps required. The table highlights the competitive performance of IR-CM, especially with only one or two inference steps.
In-depth insights#
Consistency Training#
Consistency training, a core concept in the paper, focuses on training a model to map any point along the trajectory of a stochastic differential equation (SDE) back to its origin. This differs from consistency distillation, which leverages a pre-trained model. The key advantage is independence from pre-trained checkpoints, creating a standalone, general-purpose image restoration model. The paper introduces a novel training strategy involving a linear-nonlinear decoupling, significantly improving training effectiveness. To enhance stability and avoid trivial solutions, an origin-guided loss function is incorporated. This two-stage approach—linear fitting followed by non-linear fitting—allows for fast, one-step or few-step inference, achieving competitive results and state-of-the-art performance in low-light enhancement with two steps. The origin-estimated consistency function further refines this process, enhancing stability and solution space reduction.
Fast Inference#
The research emphasizes achieving fast inference as a crucial aspect of image restoration. Traditional methods often involve multiple steps, hindering real-time applications. This work proposes a novel approach that leverages a consistency model to enable few-step or even one-step inference, significantly improving efficiency. This speedup is achieved through consistency distillation or training on specific stochastic differential equations. The model’s design prioritizes speed without sacrificing accuracy, achieving highly competitive results with only one-step inference and state-of-the-art performance with just two. The emphasis on speed and universality makes the method practical for diverse real-world image restoration tasks, potentially transforming real-time applications in areas like autonomous driving.
Universal Restoration#
The concept of “Universal Restoration” in image processing aims to create a single model capable of handling diverse image degradation types, such as noise, blur, rain, and low light. This contrasts with traditional methods which typically focus on a specific type of degradation. A universal approach offers significant advantages: reduced development effort by avoiding the need to build separate models for each scenario, increased efficiency through a single inference process, and enhanced adaptability to new, unseen degradations. However, achieving true universality presents challenges. The model must learn to identify and address the underlying causes of degradation across a wide range of visual artifacts, necessitating robust feature extraction and complex model architectures. Additionally, training such a model requires large and diverse datasets encompassing many degradation forms, potentially increasing training complexity and time. The success of a universal restoration model hinges on finding the right balance between model complexity and generalization ability to achieve both high accuracy and fast inference.
Ablation Studies#
Ablation studies systematically remove components of a model to assess their individual contributions. In the context of image restoration, this might involve removing specific modules (e.g., linear fitting, origin-guided loss), training strategies (e.g., linear-nonlinear decoupling), or specific components of a loss function. By observing the effects of these removals on metrics like PSNR, SSIM and LPIPS, researchers can understand which components are essential to achieving high performance and which might be redundant or even detrimental. This helps to identify design choices that are crucial for the effectiveness of the model and provides valuable insights into the underlying mechanisms of the image restoration process. Well-designed ablation studies are crucial for establishing the validity and robustness of a method, demonstrating that the performance improvements observed are due to the proposed components and not other factors. They enhance the transparency and trustworthiness of research by allowing other researchers to validate findings and understand the importance of the different design decisions that were made during the development of the model. Results of these studies often inform future model designs by enabling researchers to build upon successful elements and avoid unnecessary complexities.
Future Directions#
Future research could explore several promising avenues. Improving the efficiency and scalability of the training process is crucial, possibly through more advanced optimization techniques or the development of novel training strategies. Exploring different architectures, such as transformers or other deep learning models, could enhance performance and generalizability. Investigating the model’s robustness to various types of noise and degradation, beyond those evaluated in the paper, would be beneficial. Furthermore, expanding the range of image restoration tasks addressed, such as handling videos or 3D images, would widen the model’s applicability. Finally, a thorough investigation into the theoretical underpinnings of the proposed methods, including a more comprehensive mathematical analysis, would further solidify their foundations and potentially unlock even greater potential.
More visual insights#
More on figures

This figure illustrates the two-stage training strategy used in the IR-CM model. Stage one uses a simplified noise addition process for training, while stage two uses the full SDE process. The figure visually represents the data flow and transformations at each stage of the training process.

This figure illustrates the two-stage training strategy used in the IR-CM model. Stage one simplifies the forward stochastic differential equation (SDE) to a noise addition process, enabling consistency training. Stage two uses the high-quality image as a starting point, gradually degrading it to low-quality with consistency training applied at each step. This two-stage approach improves training effectiveness.

This figure shows a qualitative comparison of image deraining results from different methods on the R100L and R100H datasets. The top row displays results for the R100L dataset, while the bottom row displays results for the R100H dataset. Each column represents a different image deraining method: input (original rainy image), JORDER, MAXIM, PReNet, Restormer, IR-SDE, the proposed method (Ours), and ground truth (GT). The figure demonstrates the visual quality differences in the deraining results obtained by each approach.

This figure shows a qualitative comparison of image deraining results on the Raindrop dataset. It compares the performance of three methods: Transweather, MAXIM, and the proposed method (Ours) against the ground truth (GT). The input images show various scenes with rain streaks. Each column displays the results for a particular image, showing the input image followed by the results from the three compared methods and the ground truth. The figure visually demonstrates the effectiveness of the proposed method in removing rain streaks and restoring image clarity.

This figure shows a qualitative comparison of different image deblurring methods on the GoPro dataset. The ‘input’ column shows the blurry images. Subsequent columns display the results of DeepDeblur, DBGAN, DeblurGANv2, MAXIM, IR-SDE, and the proposed method (‘Ours’). The final column displays the ground truth (‘GT’). This visual comparison helps illustrate the relative performance of each method in terms of deblurring quality.

This figure displays the qualitative comparison results of different low-light image enhancement methods on the LOLv2 dataset. It shows input low-light images alongside the results produced by DiffLL, GlobalDiff, Retinexformer, LLFlow, IR-SDE, the proposed IR-CM method, and the ground truth (GT) images. The visual comparison allows for a qualitative assessment of the effectiveness of each method in enhancing low-light images.

This figure shows the visual results of the proposed method with different sampling steps (1-step, 2-step, 3-step, 4-step) on low-light image enhancement task. It demonstrates the improvement in image quality with increased sampling steps, comparing against the ground truth (GT) images. The input images are very dark, highlighting the effectiveness of the method in enhancing the details and brightness.

This figure shows a qualitative comparison of image deraining results from different methods on the R100L and R100H datasets. Each row represents a different image, and the columns show the input image, the results of the JORDER, MAXIM, PReNet, Restormer, IR-SDE methods, the proposed method (Ours), and the ground truth (GT). The figure highlights the visual improvements achieved by the proposed method compared to existing state-of-the-art deraining techniques. Additional results are available in Appendix D.

This figure shows a qualitative comparison of different image deraining methods on two datasets: R100L and R100H. The top row displays results on the R100L dataset, and the bottom row shows results on the R100H dataset. Each column represents a different method (JORDER, MAXIM, PReNet, Restormer, IR-SDE, Ours, Ground Truth). The figure demonstrates the visual quality of image deraining produced by each method.

This figure shows a qualitative comparison of different image deblurring methods on the GoPro dataset. The input blurry images are shown alongside the results from DeepDeblur, DBGAN, DeblurGANv2, MAXIM, IR-SDE, and the proposed IR-CM method. The ground truth (GT) deblurred images are also included for reference. The figure demonstrates the visual quality of the deblurred images produced by each method.

This figure displays visual comparisons of image denoising results using the proposed IR-CM method and the baseline IR-SDE model. The results are shown for various images with different noise levels, demonstrating the effectiveness of the proposed method in reducing noise while preserving image details. The McMaster dataset, with sigma = 25 noise level, is used as the test set for this comparison. Each row shows an input image with added noise, the results of the IR-SDE method, the results of the proposed IR-CM method, and the ground truth image, respectively.

This figure shows a qualitative comparison of different low-light image enhancement methods on the LOLv2 dataset. The methods compared include DiffLL, GlobalDiff, Retinexformer, LLFlow, IR-SDE, and the proposed method, IR-CM. The input low-light images are shown in the first column, and the enhanced images produced by each method are shown in the subsequent columns. The ground truth images are shown in the last column. This allows for visual comparison of the relative effectiveness of each method in enhancing low-light images.
More on tables
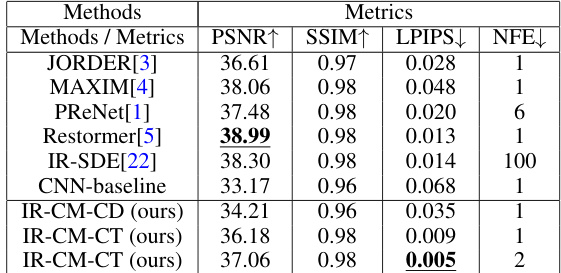
This table presents a quantitative comparison of the proposed IR-CM method with several state-of-the-art image deraining methods on the R100L dataset. The metrics used for comparison are PSNR (Peak Signal-to-Noise Ratio), SSIM (Structural Similarity Index), LPIPS (Learned Perceptual Image Patch Similarity), and NFE (Number of Function Evaluations). The table shows that IR-CM achieves competitive results, particularly with two-step inference, demonstrating its effectiveness in image deraining.
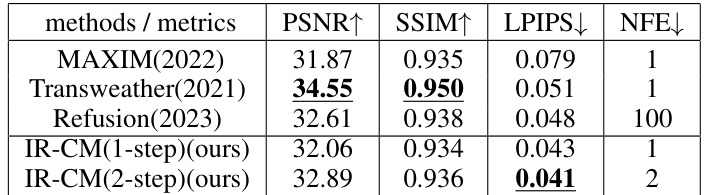
This table presents a quantitative comparison of the proposed IR-CM model’s performance on the Raindrop dataset against several state-of-the-art image deraining methods. The metrics used are PSNR, SSIM, LPIPS and NFE (Number of Function Evaluations). Higher PSNR and SSIM values indicate better performance, while a lower LPIPS value signifies improved perceptual quality. The table highlights the superior performance of the IR-CM method, especially with two-step inference, as indicated by bold underlined values.
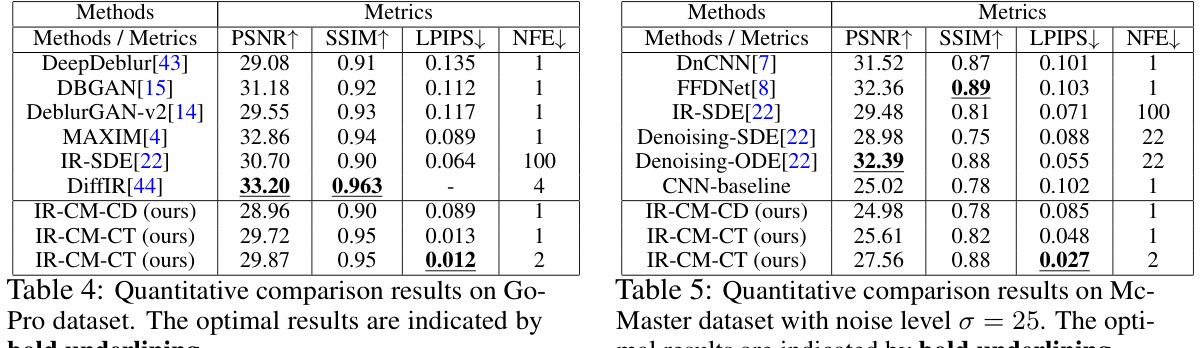
This table compares the performance of the proposed IR-CM method against several state-of-the-art image deblurring methods on the GoPro dataset. The metrics used for comparison are PSNR, SSIM, LPIPS, and NFE (Number of Function Evaluations). The table shows that IR-CM achieves competitive results, particularly excelling in perceptual quality (LPIPS). The bold underlining highlights the best performance for each metric.

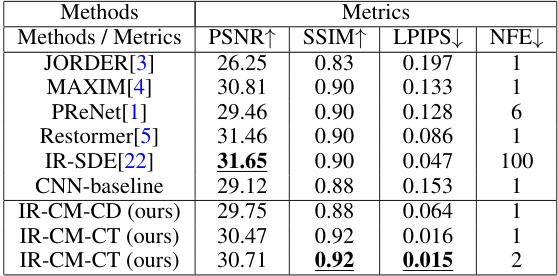
This table presents a quantitative comparison of the proposed IR-CM model with several state-of-the-art low-light image enhancement methods on the LOLv2 dataset. The metrics used for comparison include PSNR (higher is better), SSIM (higher is better), and LPIPS (lower is better), representing image quality, structural similarity, and perceptual similarity respectively. NFE represents the number of function evaluations, indicating computational cost. The table shows that the IR-CM method, especially with two-step inference, achieves superior performance compared to other methods.
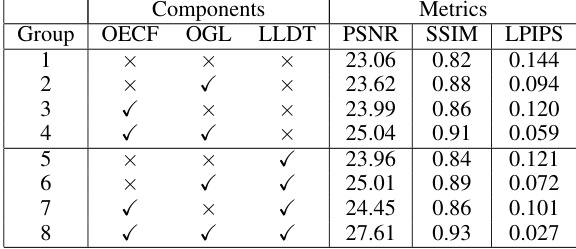
This table presents the results of ablation experiments conducted on the LOLv2 dataset to evaluate the impact of each component of the proposed IR-CM model. The components evaluated are the Origin-estimated Consistency Function (OECF), the Origin-guided Loss (OGL), and the Linear-Nonlinear Decoupling Training (LLDT) strategy. The metrics used to evaluate the model performance are PSNR, SSIM, and LPIPS.

This table compares the inference time of the proposed IR-CM model with other state-of-the-art (SOTA) methods for three different image resolutions (256x256, 600x400, and 1280x720). It shows that the IR-CM model significantly reduces inference time compared to the baseline IR-SDE, especially for larger images, while maintaining competitive performance. The table highlights the trade-off between inference speed and model performance by showing results for both one-step and two-step inference strategies of IR-CM.

This table presents the results of an ablation study on the effect of different values of the origin-guided loss weight (λOG) on the performance of the proposed model. The performance metrics used are PSNR, SSIM, and LPIPS. The results demonstrate that a λOG value of 0.8 yields the optimal performance, as indicated by the bold values in the table.

This table presents a comparison of the model’s performance using different numbers of sampling steps in low-light image enhancement. The metrics used for comparison are PSNR, SSIM, and LPIPS. The results show that using two sampling steps provides the best perceptual quality (LPIPS), while also maintaining good PSNR and SSIM scores. Increasing the number of sampling steps beyond two only provides marginal improvements.
Full paper#