↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Traditional domain generalization struggles with real-world scenarios where data distributions change continually. Existing methods often assume multiple source domains are available simultaneously, which isn’t always realistic. Furthermore, many existing solutions mainly focus on capturing the evolving patterns at the feature level, and are not robust to violations of distribution assumptions. This poses a significant challenge for developing robust and practical machine learning models.
This paper introduces Weight Diffusion (W-Diff), a novel framework addressing the above limitations. W-Diff uses a conditional diffusion model to learn evolving patterns in classifier weights, learning dynamic patterns from historical data and generating customized classifiers for future domains. This novel approach outperforms existing methods on various datasets. It also learns a domain-shared feature encoder which helps reduce overfitting and improves generalization. The ensemble approach, using multiple generated classifiers, enhances prediction robustness. The results demonstrate W-Diff’s superior ability in generalization on unseen future domains.
Key Takeaways#
Why does it matter?#
This paper is crucial because it tackles the challenge of evolving domain generalization in a domain-incremental setting, a largely unexplored area. It introduces a novel framework that uses conditional diffusion models, a powerful tool in generative modeling, to learn dynamic patterns in the classifier weights. By enabling generalization on unseen future data, this research significantly advances continual learning, potentially impacting various applications such as robotics and autonomous systems.
Visual Insights#

This figure illustrates the overall architecture of the proposed Weight Diffusion (W-Diff) model. It shows how the model uses reference points from historical domains, anchor points from the current domain, and prototype information to train a conditional diffusion model. This model then generates customized classifiers for future domains. The figure also highlights the use of prediction consistency loss to learn a domain-shared feature space, preventing overfitting.
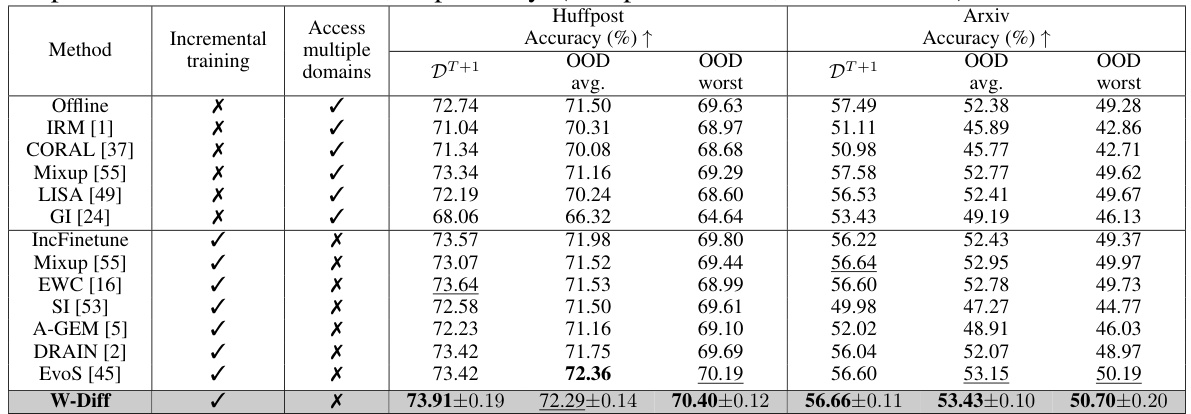
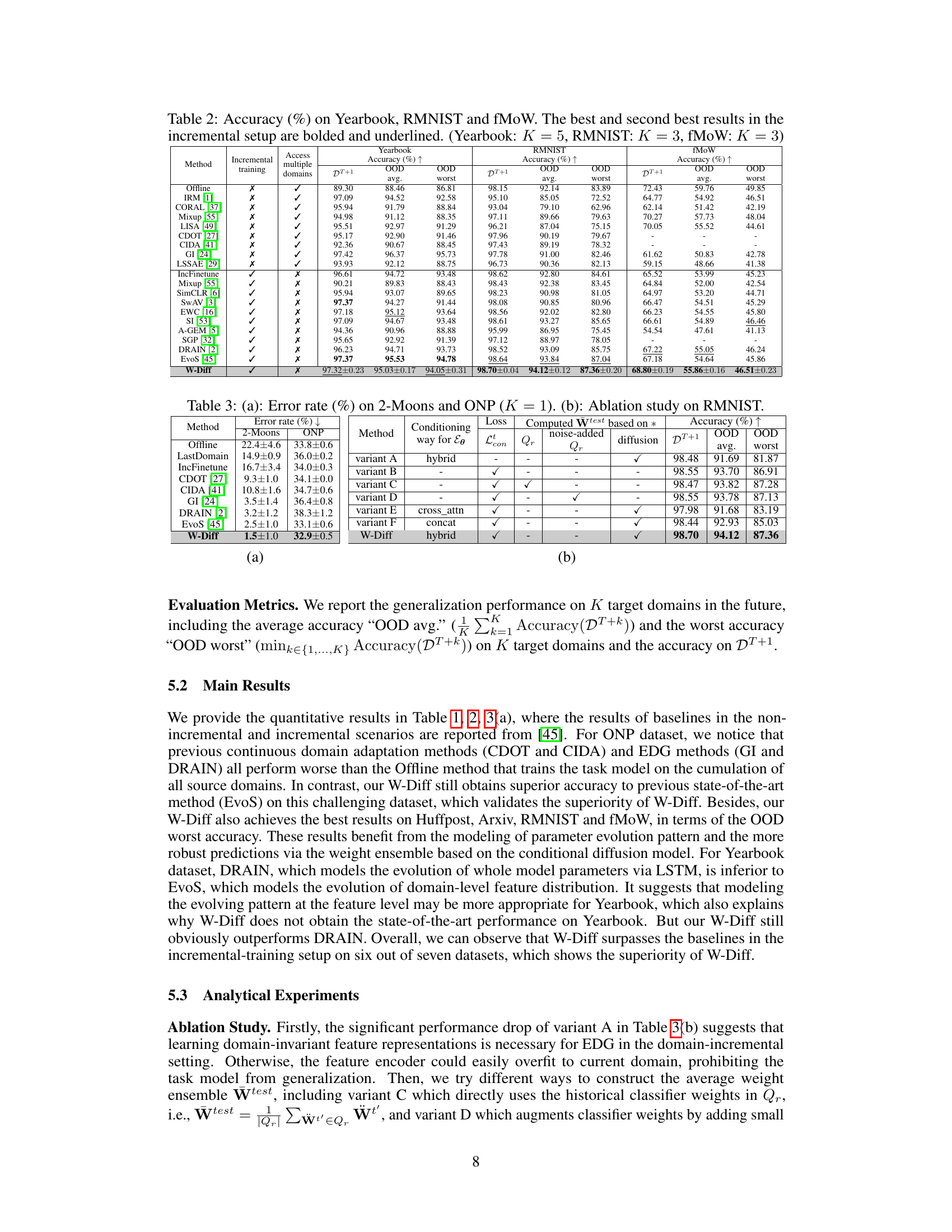
This table presents the accuracy results of different domain generalization methods on the Huffpost and Arxiv datasets. The results are broken down by whether the method used incremental training, access to multiple domains, and the accuracy on the next unseen domain (DT+1), average accuracy over unseen domains, and worst accuracy over unseen domains. The best and second-best performing methods in the incremental setting are highlighted.
In-depth insights#
W-Diff Framework#
The W-Diff framework introduces a novel approach to evolving domain generalization (EDG) in a domain-incremental setting. It leverages conditional diffusion models to learn the evolving patterns of classifier weights across sequentially arriving domains. Unlike methods assuming simultaneous availability of source domains, W-Diff maintains a queue of historical classifier weights, using them as reference points. The framework conditions the diffusion process on these reference weights and the prototypes of the current domain, generating updates that effectively bridge the gap between historical and current classifier parameters. A domain-shared feature encoder ensures consistent predictions across domains, mitigating overfitting. During inference, W-Diff ensembles many target domain-customized classifiers generated via the diffusion model, resulting in robust and accurate predictions. This unique combination of conditional diffusion models, historical weight referencing, and ensemble prediction makes W-Diff particularly effective in handling the challenges of non-stationary environments with dynamically evolving data distributions. The reliance on a parameter-level approach, rather than a feature-level approach, is also a significant differentiator.
Diffusion Modeling#
Diffusion models offer a powerful generative approach by reversing a noise diffusion process. The core idea involves gradually adding Gaussian noise to data until it becomes pure noise, then learning to reverse this process to generate new data samples. Conditional diffusion models extend this by incorporating additional information, such as class labels or text prompts, to guide the generation process, producing more targeted and controlled outputs. This conditioning is crucial in applications such as image generation and parameter generation in machine learning models, allowing for fine-grained control over the generated samples. The ability to model complex data distributions and generate high-quality samples makes diffusion models a compelling area of research in generative AI. However, challenges remain, including computational cost and the need for effective ways to handle large datasets and complex conditioning information. Further research could explore more efficient architectures and training strategies, and investigate novel ways to utilize the inherent properties of diffusion models in diverse applications. The potential applications are vast and span numerous domains, promising a significant impact on various fields.
Incremental EDG#
Incremental evolving domain generalization (EDG) tackles the challenge of adapting machine learning models to progressively changing data distributions. Unlike traditional EDG, which often assumes the availability of multiple source domains simultaneously, the incremental approach addresses the more realistic scenario where domains arrive sequentially. This poses significant challenges, as models must learn from each new domain without forgetting previously learned information (catastrophic forgetting). Effective strategies are needed to manage the accumulation of knowledge across multiple domains. A critical aspect is identifying and capturing the underlying pattern of how data distributions evolve, enabling robust generalization to future, unseen domains. Successful approaches might employ mechanisms such as memory management techniques to store and retrieve relevant past information, regularization methods to prevent overfitting and catastrophic forgetting, and learning paradigms that explicitly model the dynamic changes in data distributions. This could involve advanced techniques such as continual learning, transfer learning, and meta-learning. Research in incremental EDG is crucial for building robust and adaptable AI systems capable of functioning effectively in real-world, dynamic environments.
Parameter Evolution#
The concept of “Parameter Evolution” in the context of deep learning models tackling non-stationary environments is crucial. It highlights the dynamic adaptation of model parameters over time, mirroring the evolving data distributions. This contrasts with traditional domain generalization, which often assumes static data distributions across domains. The core idea revolves around learning the patterns of parameter change rather than simply retraining the entire model for each new domain. This involves sophisticated techniques like employing diffusion models which can generate updated parameters conditioned on historical parameters and current data characteristics. This conditional parameter generation approach is beneficial because it allows for efficient adaptation to new environments. The key is capturing the underlying structure of parameter shifts to predict future parameter values, enhancing generalization to unseen future data. Effectively leveraging historical data is critical for this, often requiring careful storage and management to avoid the computational cost of retraining from scratch. Overall, “Parameter Evolution” represents a powerful paradigm shift towards more adaptable and robust deep learning systems in dynamic real-world settings.
Future Directions#
Future research directions stemming from this evolving domain generalization (EDG) work could explore several key areas. Extending W-Diff to handle more complex tasks beyond classification is crucial, such as regression or structured prediction problems. Improving the efficiency and scalability of the conditional diffusion model is another significant direction, perhaps through exploring more efficient diffusion architectures or leveraging techniques like quantization to reduce memory footprint and speed up inference. Investigating the impact of different noise schedules and variance schedules on the performance of W-Diff warrants further research. The robustness of W-Diff to noisy or incomplete data needs to be thoroughly investigated, especially considering the domain-incremental setting where data quality might vary across domains. Finally, a theoretical analysis of W-Diff’s generalization properties would offer valuable insight and potentially guide the development of more principled methods. Addressing these areas will not only enhance the practical applicability of W-Diff but will also further advance the understanding and development of EDG techniques.
More visual insights#
More on figures

This figure illustrates the overall architecture of the W-Diff model, highlighting the key components: task model training, weight diffusion training, and inference. The training process involves maintaining queues for reference points (historical classifier weights), anchor points (current classifier weights), and prototypes (domain representations). The weight diffusion uses a conditional diffusion model to learn the evolving pattern of the classifier weights based on the reference and anchor points. During inference, the model generates customized classifiers for unseen domains using the learned diffusion model and a weights ensemble strategy.
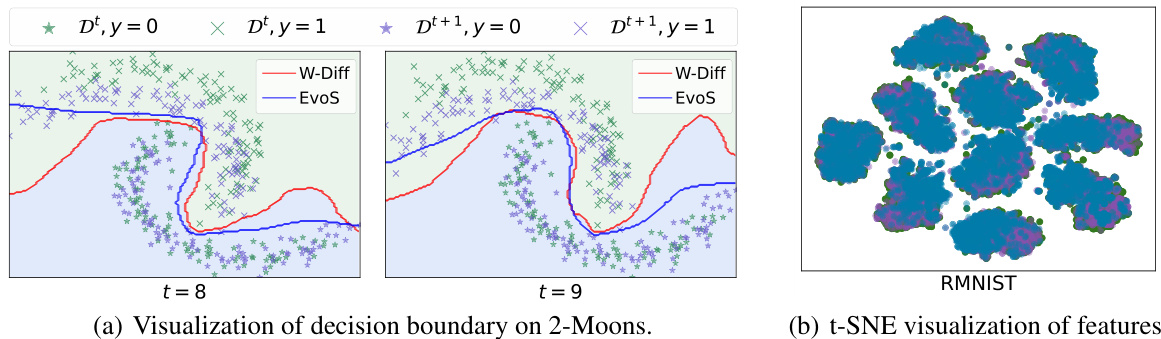
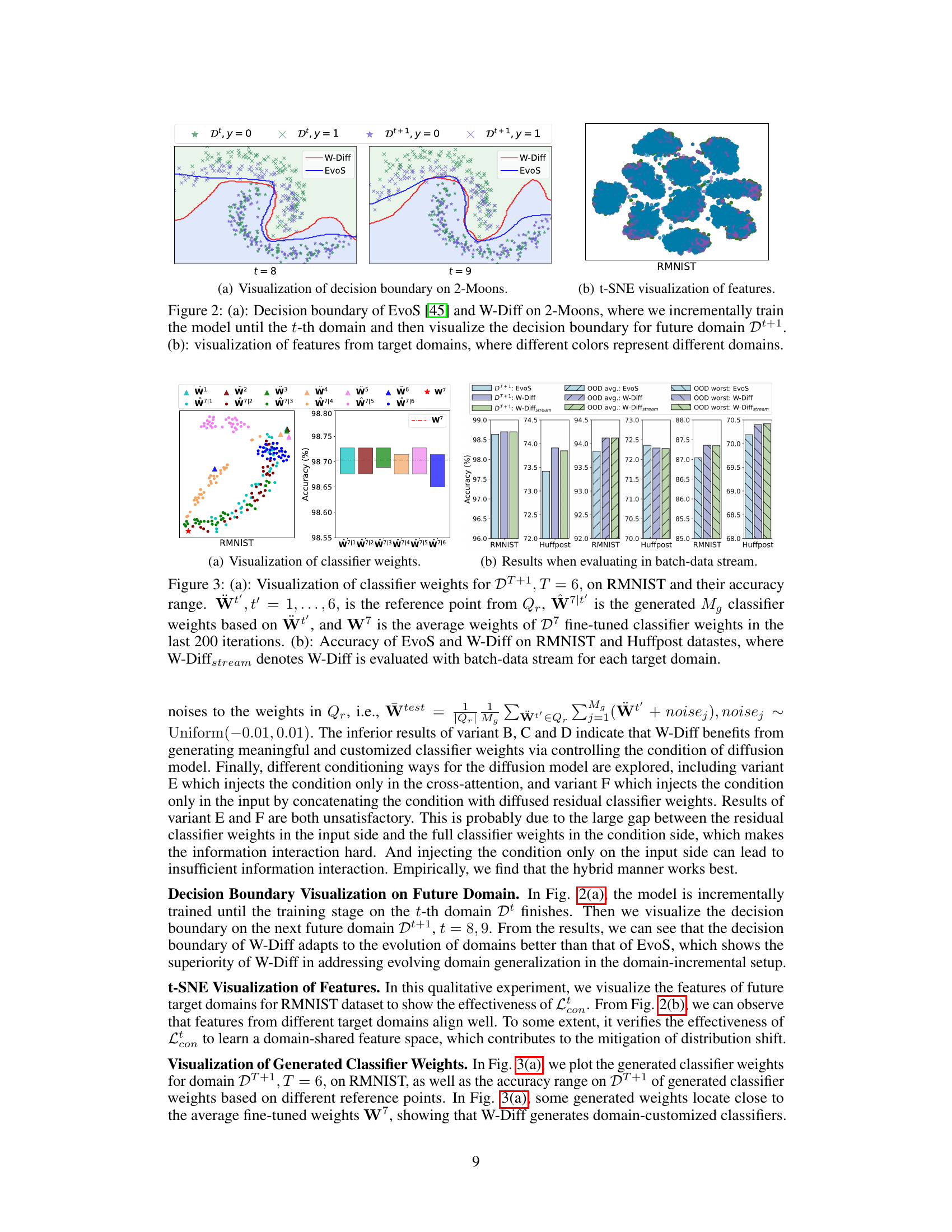
This figure shows a comparison between EvoS and W-Diff on a 2-Moons dataset. The left panel (a) visualizes the decision boundaries of both methods for future domains (Dt+1) after incremental training up to domain t=8 and t=9. The right panel (b) displays a t-SNE visualization of features extracted from the target domains, illustrating how well the models separate features from different domains. The different colors indicate different domains.
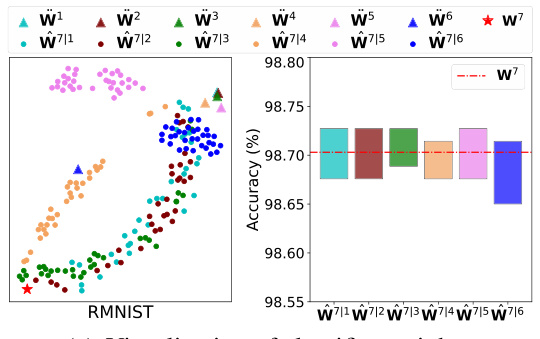
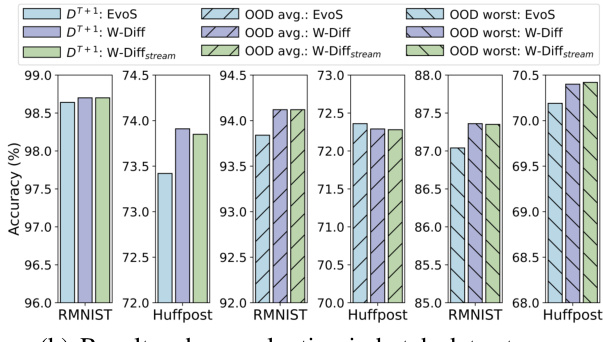
This figure visualizes the classifier weights generated by the W-Diff model for a target domain (DT+1) on the RMNIST dataset. Panel (a) shows the generated weights (W7|t’) plotted against reference points from the queue Qr (Ŵt’), illustrating the model’s ability to generate domain-specific weights. The accuracy range of the generated weights is also shown. Panel (b) compares the performance of W-Diff and EvoS on RMNIST and Huffpost, highlighting the improvement achieved by W-Diff’s approach of using a batch data stream during evaluation.
This figure provides a visual overview of the Weight Diffusion (W-Diff) model proposed in the paper. It illustrates the different components of the model, including the reference point queue (Qr), anchor point queue (Qa), prototype queue (Qp), feature encoder (Eψ), conditional diffusion model (Eθ), and the loss functions used for training. The figure shows how the model learns the evolving pattern of classifiers across domains and how it generates customized classifiers for unseen domains.
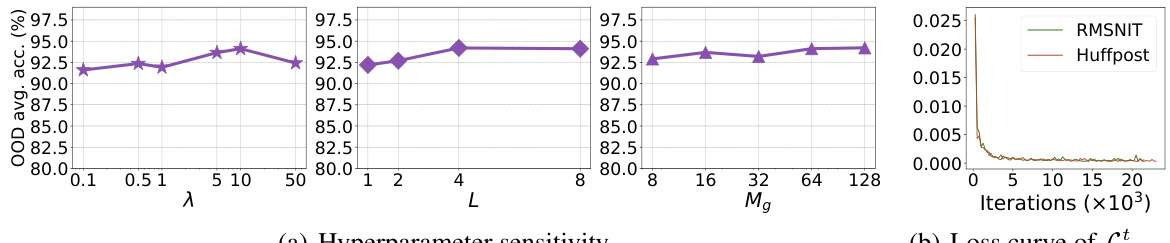
This figure shows the overall architecture of the proposed Weight Diffusion (W-Diff) model for evolving domain generalization. It highlights the key components: the task model training, the weight diffusion process, and the inference stage. It also illustrates the role of different queues (reference point queue Qr, anchor point queue Qa, and prototype queue Qp) in maintaining the information needed for training the conditional diffusion model. The figure also depicts the use of both prediction consistency loss and cross-entropy loss during training, along with the conditional diffusion model’s use of a noise estimation error loss.
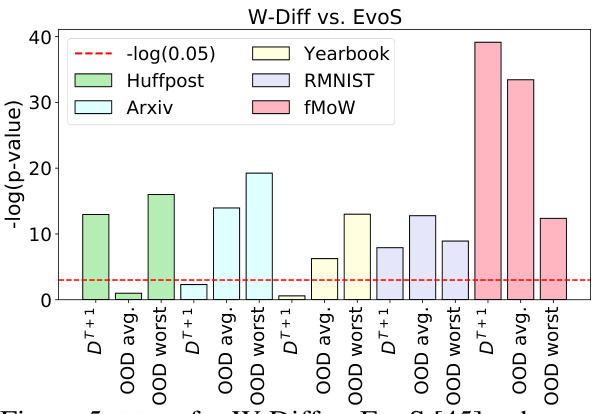
This figure shows the results of t-tests comparing the performance of W-Diff and EvoS on five different datasets (Huffpost, Arxiv, Yearbook, RMNIST, fMoW) for three different metrics: accuracy on the first unseen target domain (DT+1), average accuracy across all unseen target domains (OOD avg.), and the worst accuracy across all unseen target domains (OOD worst). The significance level (alpha) is set at 0.05. A p-value below 0.05 indicates a statistically significant difference between the two methods for that particular metric and dataset. The graph plots -log10(p-value) for each dataset and metric; values above the red dashed line (-log10(0.05) ≈ 1.3) indicate statistically significant superiority of W-Diff over EvoS.
More on tables
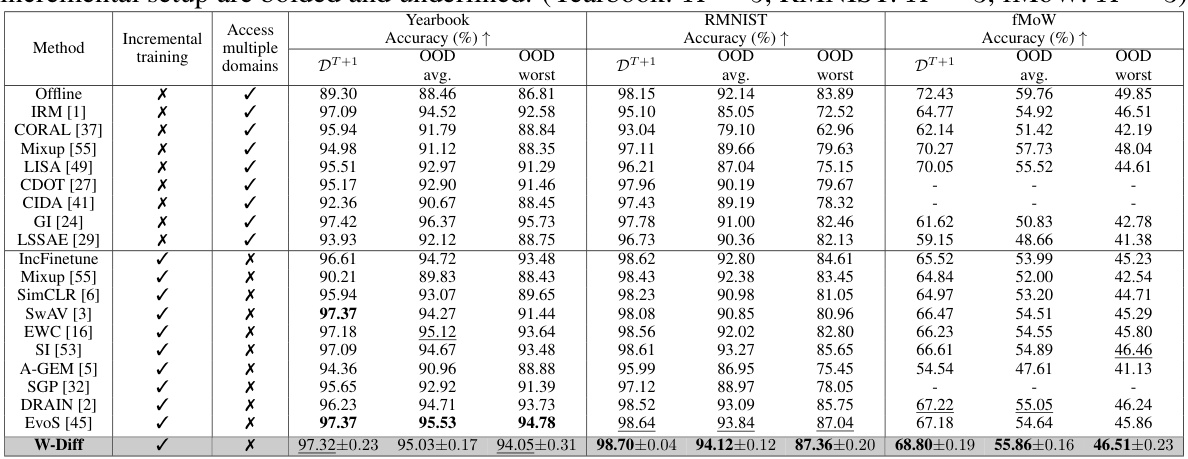
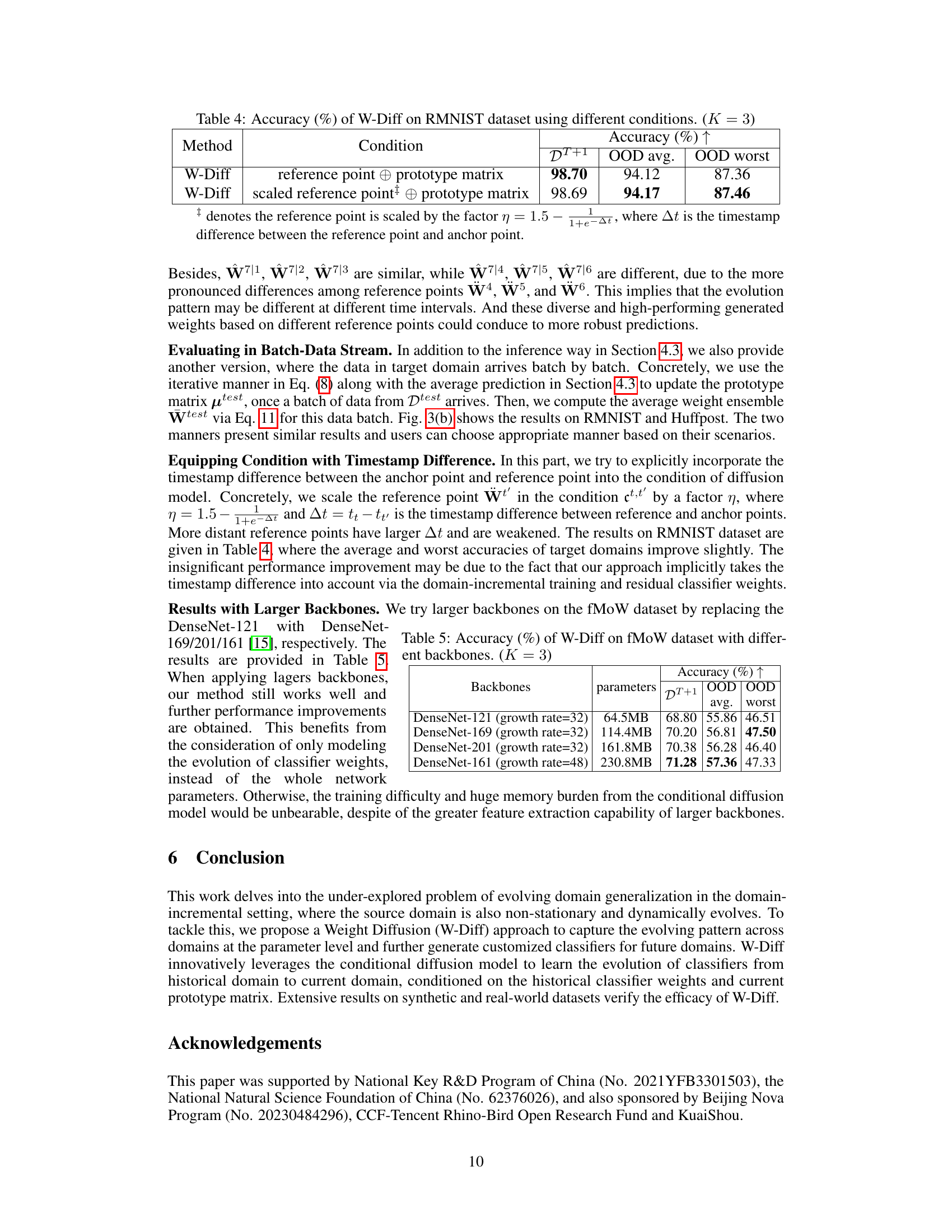
This table presents the accuracy results of different domain generalization methods on three image datasets: Yearbook, RMNIST, and fMoW. It compares the performance of these methods in both incremental and non-incremental training settings, showing the average and worst accuracy across out-of-distribution (OOD) test domains. The best and second-best performing methods for each dataset and setting are highlighted. The table helps illustrate the effectiveness of incremental learning and the relative performance of various approaches.
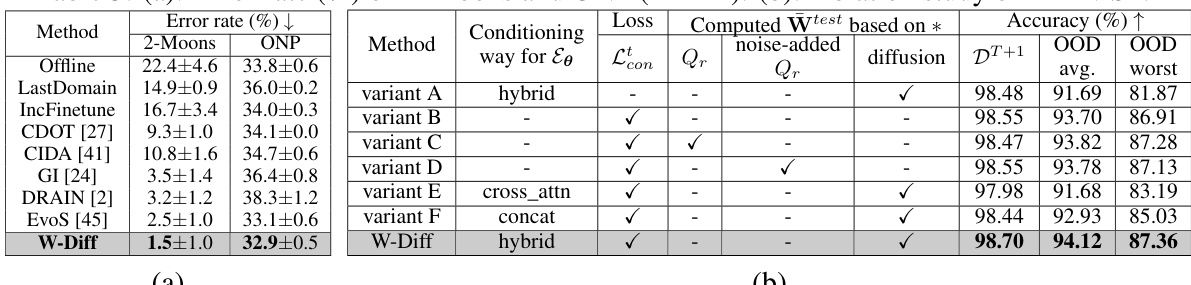
Table 3 presents the results of two experiments. In (a), the error rates of different methods on the 2-Moons and ONP datasets are reported. In (b), an ablation study on RMNIST is conducted, analyzing the impact of different components of W-Diff on its performance.

This table presents the accuracy results of the W-Diff model on the RMNIST dataset under different conditions. Two conditions are tested: using the reference point and prototype matrix, and using a scaled reference point and prototype matrix. The accuracy is evaluated for the immediate next domain (DT+1) and the average and worst accuracy over multiple unseen future domains (OOD avg. and OOD worst). The results show that using a scaled reference point slightly improves the overall performance.
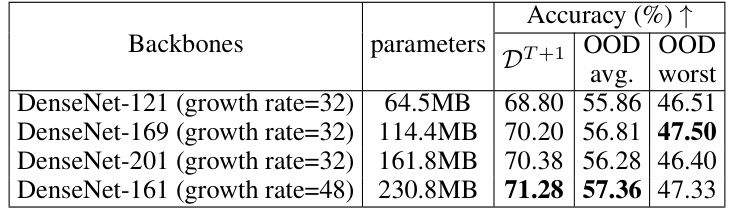
This table shows the accuracy of the W-Diff model on the fMoW dataset using different DenseNet backbones. It presents the accuracy on the first unseen target domain (DT+1) and the average and worst accuracy across all unseen target domains (OOD avg. and OOD worst). The number of parameters for each backbone is also included to illustrate the trade-off between model complexity and performance.

This table presents the accuracy results of various domain generalization methods on the Huffpost and Arxiv datasets. It compares the performance of these methods in both an offline setting (where all domains are available for training) and an incremental setting (where domains arrive sequentially). The best and second-best results in the incremental setting are highlighted, providing a clear comparison of performance across different approaches under varying data availability scenarios. K represents the number of target domains.

This table shows the accuracy of different domain generalization methods on the Huffpost and Arxiv datasets. The results are broken down by whether the methods were trained incrementally and whether they had access to multiple domains. The best and second-best results for incremental training are highlighted. The number of target domains (K) is also specified for each dataset.

This table presents the accuracy results of several domain generalization methods on the Huffpost and Arxiv datasets. The results are categorized by whether the methods allow for access to multiple domains simultaneously or only allow access to sequentially arriving domains. For each method, average and worst-case accuracy across out-of-distribution (OOD) target domains are shown. The best-performing methods in the incremental setup (meaning only sequentially arriving domains are considered) are highlighted.
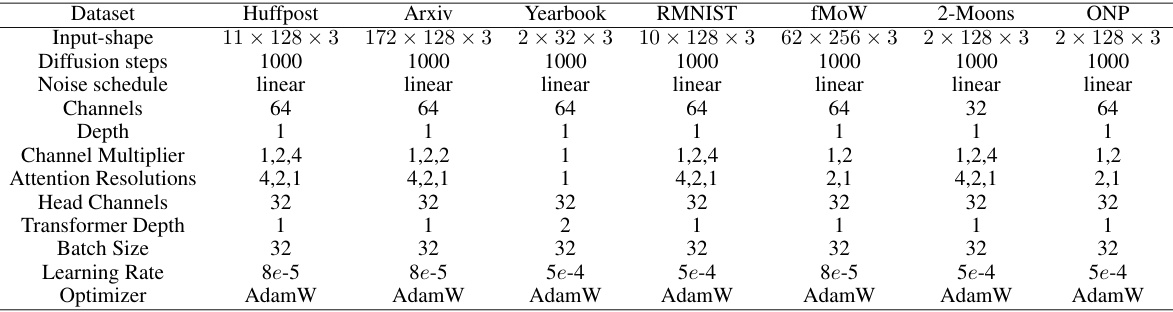
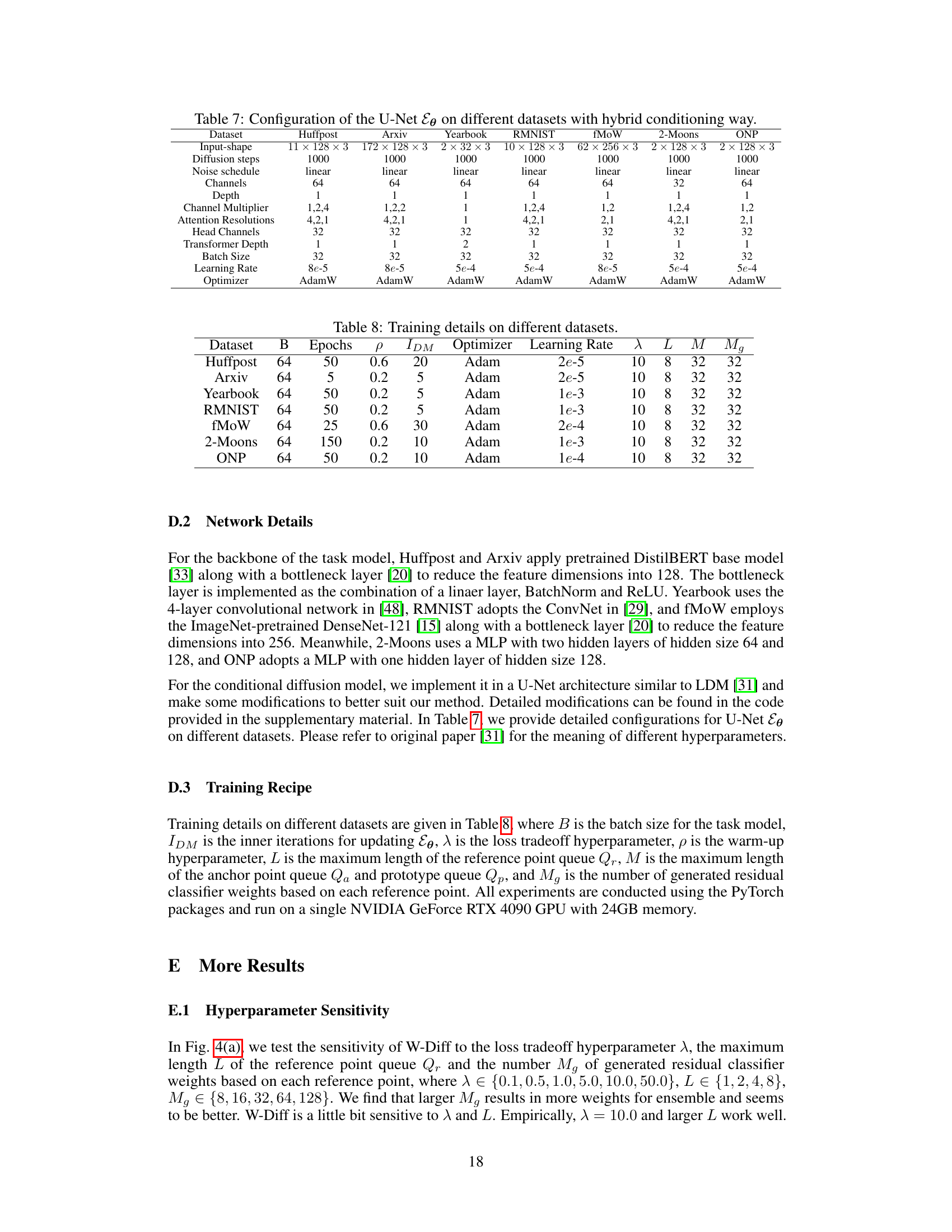
This table details the hyperparameters used for the U-Net architecture of the conditional diffusion model (Ee). The table breaks down the configurations based on the specific dataset used, including input shape, diffusion steps, noise schedule, channel settings, depth, attention resolutions, head channels, and transformer depth. It also lists the batch size, learning rate, and optimizer used for training the model for each dataset. These settings were optimized for each dataset separately to improve the quality of the generated model weights.

This table lists the hyperparameters used for training the task model and conditional diffusion model on eight different datasets. The hyperparameters include batch size, number of epochs, warm-up hyperparameter, inner iterations for diffusion model training, optimizer, learning rate, loss tradeoff hyperparameter, maximum length of the reference point queue, maximum length of the anchor and prototype queues, and number of generated residual classifier weights.

This table shows the memory cost (in MB) and inference time (in seconds) required for the conditional diffusion model to generate 32 residual classifier weights within a batch, using a denoising step of 1000. The results are broken down for different datasets: Yearbook, RMNIST, fMoW, Huffpost, Arxiv, 2-Moons, and ONP.
Full paper#