↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Optimizing functions on curved spaces like Lie groups poses challenges for traditional methods. Existing approaches often involve computationally expensive operations like parallel transport or require strong assumptions about the function’s properties. This lack of efficient and theoretically sound methods hinders progress in areas such as machine learning with orthonormal constraints or eigenvalue computation.
This research introduces and analyzes two new algorithms for Lie group optimization: Lie Heavy-Ball and Lie NAG-SC. The study rigorously quantifies their convergence rates under standard assumptions. Lie NAG-SC is shown to provide acceleration, outperforming the momentum-less case and existing manifold optimizers in computational cost and ease of implementation by leveraging the group structure. The findings demonstrate that choosing the right discretization is crucial for efficient Lie group optimization.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in optimization and machine learning due to its novel quantitative analysis of Lie group momentum optimizers and introduction of a new algorithm (Lie NAG-SC) with provable acceleration. It bridges the gap between theoretical understanding and practical applications, offering computationally efficient methods for manifold optimization problems.
Visual Insights#
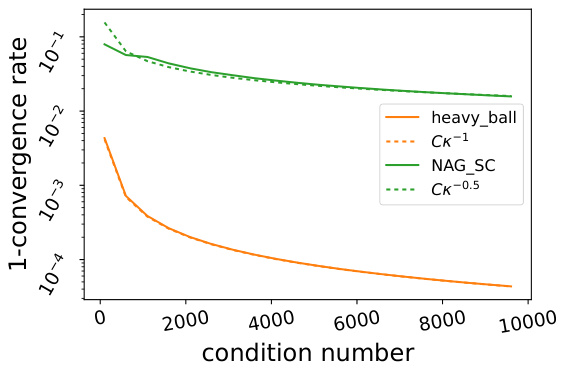
This figure compares the performance of Lie NAG-SC and Lie Heavy-Ball on two different tasks: (a) measuring convergence speed on ill-conditioned problems, and (b) finding the global minimum of a non-convex potential. The results in (a) show that Lie NAG-SC converges faster and matches theoretical predictions. The results in (b) demonstrate that Lie NAG-SC is effective in escaping local minima on non-convex problems, but does not conclusively prove superior performance to Lie Heavy-Ball in all cases.

This table summarizes the main results of the paper by comparing three different optimization schemes: continuous dynamics, Heavy-Ball, and NAG-SC. For each scheme, it shows the corresponding continuous-time dynamics equation, the step size used for discretization, the convergence rate achieved, the modified energy function used in the analysis, and the main theorem that proves the convergence rate. The table highlights the key differences between the schemes, particularly regarding their convergence rates and the computational cost associated with them.
In-depth insights#
Lie Group Optimization#
Lie group optimization offers a powerful framework for tackling optimization problems where the solution space possesses a group structure. This is particularly useful when dealing with non-Euclidean spaces, such as rotation matrices (SO(n)) or orthogonal matrices (Stiefel manifolds). By leveraging the group’s inherent properties, such as its manifold structure, Lie group optimization algorithms can achieve more efficient convergence and structure-preserving solutions. One major advantage is the potential for computational speed-up, because the algorithms often avoid costly operations such as parallel transport or geodesic computations, typically found in generic manifold optimization techniques. However, the effectiveness depends heavily on the specific problem and careful consideration of the group’s properties. Selecting an appropriate optimization algorithm within the Lie group framework, and ensuring the objective function is compatible with the chosen group structure, are crucial steps for successful application. Furthermore, convergence analysis and theoretical guarantees within Lie group optimization can be complex and problem-dependent, requiring a nuanced understanding of both the chosen algorithm and the properties of the underlying Lie group.
Momentum Analysis#
A thorough momentum analysis in a research paper would delve into the theoretical underpinnings of momentum-based optimization algorithms. It would likely begin by establishing a clear definition of momentum within the context of the specific optimization problem being addressed, often highlighting the differences and similarities between first-order and higher-order methods. A key aspect would be the mathematical analysis of convergence rates, demonstrating how momentum accelerates the optimization process compared to gradient descent alone. This often involves rigorous proofs and derivations, supported by assumptions such as strong convexity or smoothness of the objective function. The analysis should also consider the influence of hyperparameters, such as momentum coefficient and learning rate, on the convergence behavior. Finally, a comprehensive momentum analysis should compare and contrast the proposed method with existing state-of-the-art techniques. The analysis should not only examine the theoretical aspects, but also provide empirical validation through experiments that demonstrate the algorithm’s performance on benchmark datasets. This could involve comparing different momentum-based approaches or analyzing the trade-offs between acceleration and computational cost. Overall, a robust momentum analysis requires a combination of theoretical rigor and practical insights.
NAG-SC Acceleration#
The concept of NAG-SC acceleration within the context of Lie group optimization is a significant contribution. It builds upon the existing momentum-based dynamics by introducing a novel discretization scheme. This discretization, unlike previous methods, provably achieves acceleration in convergence rates, overcoming limitations of simpler schemes like Lie Heavy-Ball which do not demonstrate comparable speedups. The theoretical analysis supporting NAG-SC’s acceleration is rigorous, relying on carefully defined smoothness and convexity assumptions tailored to the curved geometry of Lie groups. The reliance on only gradient oracles and exponential maps, avoiding computationally expensive operations like parallel transport, is a key advantage making NAG-SC practically appealing. The effectiveness of NAG-SC is further validated through numerical experiments that showcase its improved performance over alternatives, particularly in high-dimensional or ill-conditioned scenarios. Overall, NAG-SC represents a substantial advancement in the field, offering a computationally efficient and theoretically sound method for optimizing functions defined on Lie groups.
Convergence Rates#
The analysis of convergence rates in optimization algorithms is crucial for understanding their efficiency and effectiveness. Quantifying convergence rates provides insights into how quickly an algorithm approaches a solution, allowing for comparisons between different methods and informing decisions about algorithm selection. The paper likely explores various convergence rates under different assumptions, such as smoothness and strong convexity. A significant contribution might involve deriving novel convergence rates for proposed Lie group momentum optimizers, perhaps demonstrating improvements over existing methods. The investigation would likely contrast the convergence behaviors of different optimization schemes (e.g., Lie Heavy-Ball vs. Lie NAG-SC), showing the impact of algorithmic choices on convergence speed. The findings are valuable because they offer theoretical guarantees on performance, providing a strong foundation for the practical application of these algorithms.
Vision Transformer#
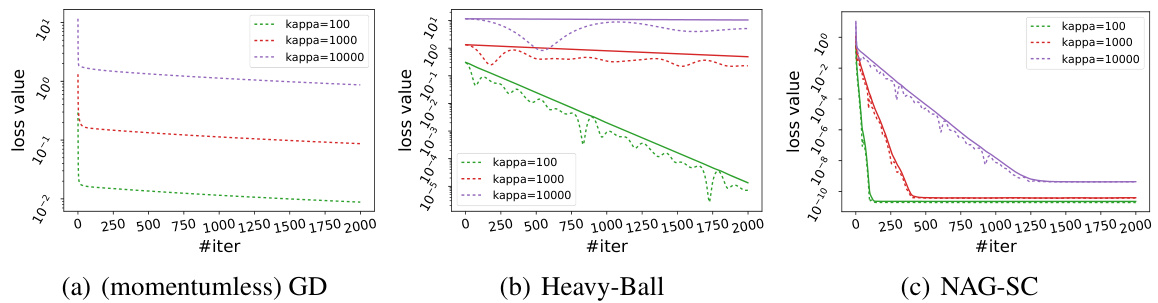
The section on “Vision Transformer” showcases the practical application of the developed Lie group optimizers, specifically Lie NAG-SC, to a real-world deep learning problem. It highlights the use of orthogonal constraints in transformer models’ attention layers to enhance performance by preventing linearly dependent correlations between tokens. The authors demonstrate how their optimizer improves training and validation error rates on vision transformer models, compared to existing methods such as Euclidean SGD and Lie Heavy-Ball. This application underscores the effectiveness of Lie NAG-SC in handling the non-convex optimization challenges inherent in such models, further validating its theoretical advantages demonstrated in the earlier sections. The empirical results reinforce the claim that Lie NAG-SC offers faster convergence and improved accuracy compared to traditional optimizers, especially when dealing with ill-conditioned problems commonly encountered in deep learning.
More visual insights#
More on figures

The figure shows two subfigures. Subfigure (a) compares the convergence speed of Lie NAG-SC and Lie Heavy-Ball methods under different condition numbers. The results show that Lie NAG-SC converges significantly faster than Lie Heavy-Ball, especially when the condition number is high, which aligns with the theoretical analysis presented in the paper. Subfigure (b) illustrates the global convergence behavior of both methods on a non-convex potential function, starting from an initial point close to the global maximum. The plot depicts the function value along the optimization trajectory, demonstrating that Lie NAG-SC successfully reaches the global minimum without getting stuck in local minima. The experiment supports the claim that Lie NAG-SC exhibits superior performance compared to Lie Heavy-Ball, particularly in challenging optimization scenarios.
This figure contains two subfigures that show the convergence rate of the Lie Heavy-Ball and Lie NAG-SC algorithms. Subfigure (a) shows that Lie NAG-SC converges faster than Lie Heavy-Ball, especially when the condition number is high. Subfigure (b) shows the convergence behavior of the two algorithms on a non-convex potential function. The results indicate that Lie NAG-SC is able to find the global minimum more effectively than Lie Heavy-Ball.

This figure contains two subfigures. Subfigure (a) shows the comparison of convergence rate between Lie NAG-SC and Lie Heavy-Ball with different condition numbers. The results show that Lie NAG-SC converges much faster than Lie Heavy-Ball, especially when the condition number is large. The experimental results match the theoretical analysis well. Subfigure (b) shows the convergence performance on a non-convex potential. Lie NAG-SC outperforms Lie Heavy-Ball and successfully finds the global minimum without being trapped in local minimums. The Lyapunov function is not shown because it is not globally defined.
More on tables
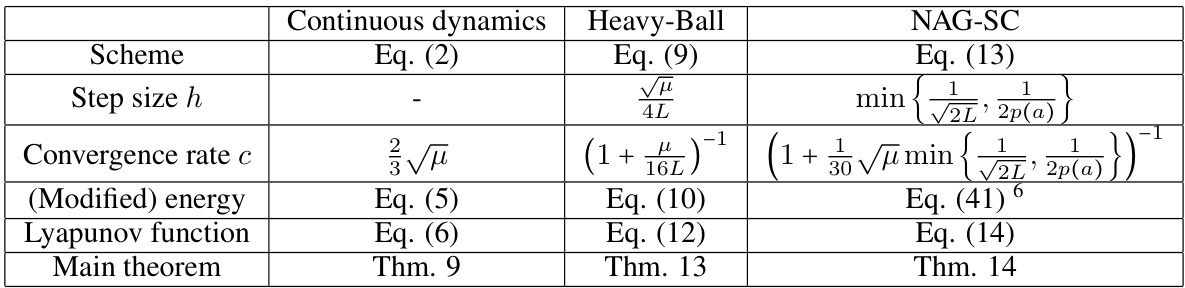
This table summarizes the main findings of the paper by comparing the continuous-time dynamics, Heavy-Ball, and NAG-SC optimizers. It shows the scheme (equation number in the paper), step size (h), convergence rate (c), modified energy function (equation number), Lyapunov function (equation number), and the main theorem supporting each convergence result.

This table summarizes the main results of the paper. It compares the continuous-time dynamics, Lie Heavy-Ball, and Lie NAG-SC optimizers in terms of their step size (h), convergence rate (c), modified energy function, and the main theorem that proves the convergence rate. It highlights the acceleration achieved by Lie NAG-SC compared to Lie Heavy-Ball and the convergence rate of Lie GD (identical to Riemannian GD on Lie Groups).

This table summarizes the main results of the paper, comparing the continuous dynamics, Heavy-Ball, and NAG-SC optimization schemes. It shows the equations used for each scheme, the step size, convergence rate, modified energy, Lyapunov function, and the main theorem supporting each.
Full paper#