Multi-language Diversity Benefits Autoformalization

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in autoformalization and related fields because it addresses the critical issue of data scarcity. By introducing MMA, a large, multilingual dataset of informal-formal mathematical pairs, it significantly improves the performance of autoformalization models. This opens new avenues for research by enabling the training of more robust and capable models for translating natural language mathematics into machine-verifiable forms. The methodology presented can inspire the creation of similar datasets for other domains and languages, broadening the scope of applications for autoformalization.

Visual Insights

#

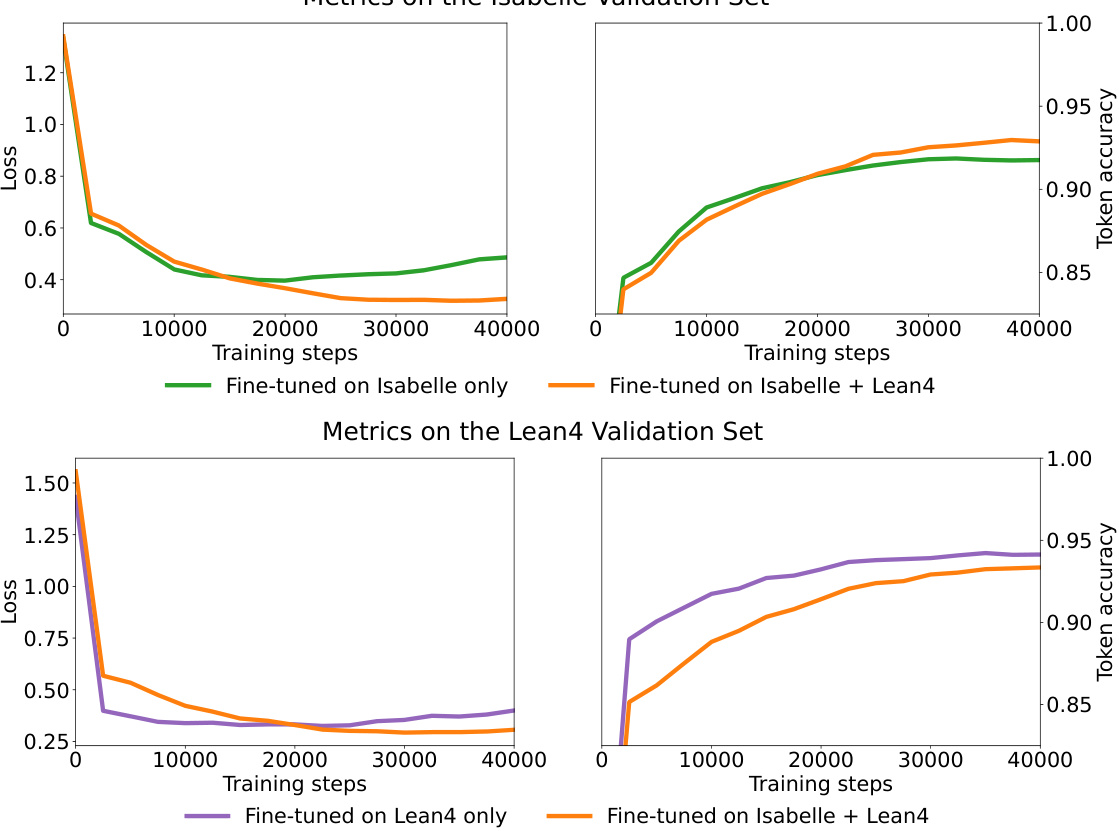
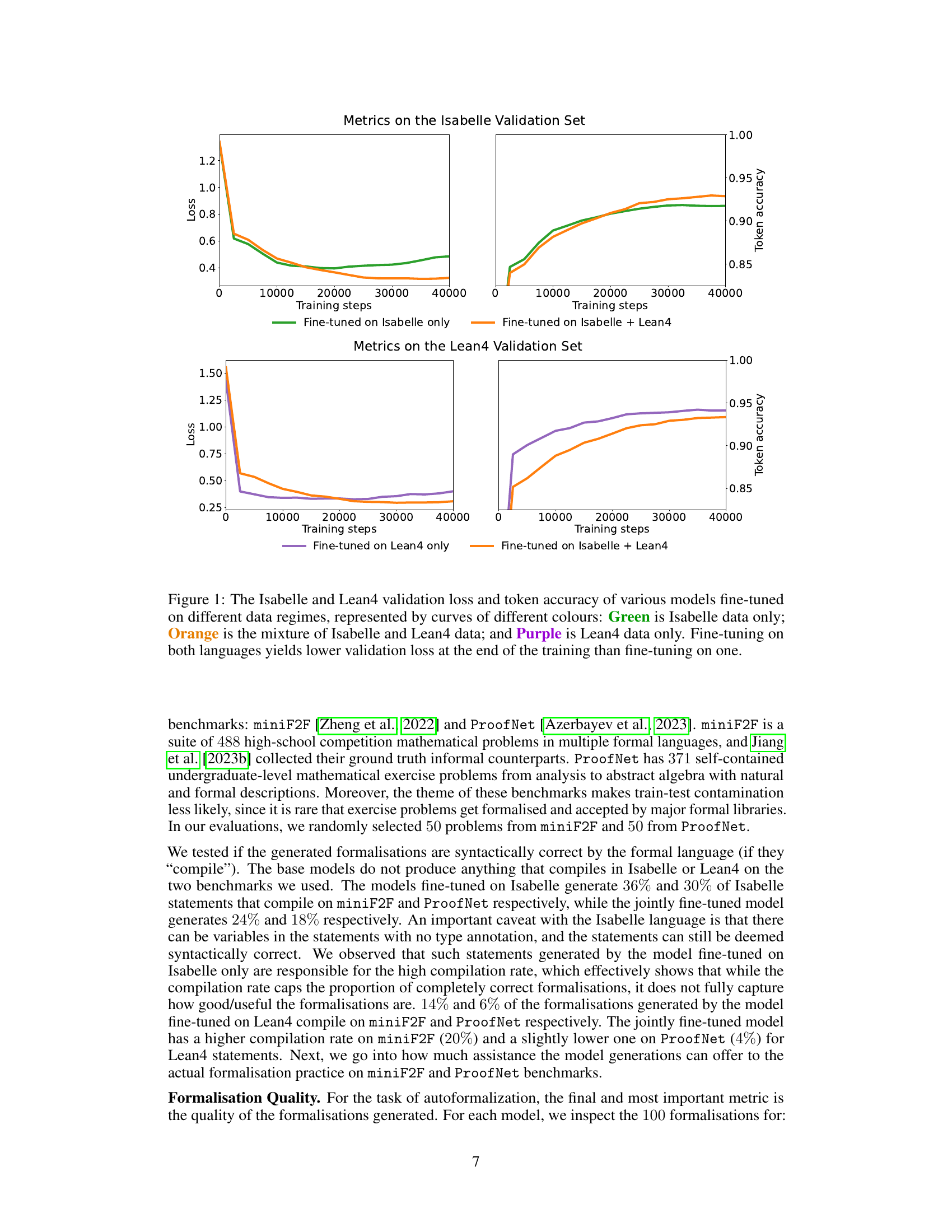
This figure shows the training curves for three different fine-tuning regimes on two language models (Isabelle and Lean4). The x-axis represents the number of training steps, while the y-axis shows both the validation loss and token accuracy. The three regimes are: fine-tuning on Isabelle data only (green), fine-tuning on a mixture of Isabelle and Lean4 data (orange), and fine-tuning on Lean4 data only (purple). The results indicate that fine-tuning on both languages leads to lower validation loss and comparable token accuracy compared to fine-tuning on a single language.

This table shows four examples of informal-formal pairs from the MMA dataset. Each row presents an Isabelle statement, a Lean4 statement, and their corresponding informal paraphrases generated by GPT-4. These examples illustrate the diversity of mathematical expressions included in the MMA dataset and the quality of the GPT-4 generated informalizations.

In-depth insights

#

Multi-lingual Autoformalization

#

Multi-lingual autoformalization presents a significant advancement in the field of automated reasoning. By leveraging the power of large language models and a diverse, multi-lingual dataset, it tackles the long-standing challenge of translating informal mathematical statements into machine-verifiable formal languages. This approach offers a scalable solution to the data scarcity problem that has plagued previous autoformalization methods. The use of multiple languages during model training demonstrates enhanced performance, highlighting the potential for transfer learning between formal languages. This opens up exciting possibilities for expanding the scope of formalized mathematics, bridging the gap between human-readable content and machine-processable knowledge. The resulting models are more capable of producing high-quality formalizations, thus enabling the automated verification and reasoning of a wider range of mathematical works. Further investigation into leveraging the strengths of multi-lingual data for autoformalization is crucial for advancing mathematical research. Moreover, releasing these new datasets and models enables collaboration and advancement in the field.

MMA Dataset Creation

#

The creation of the MMA dataset is a crucial contribution of this work, addressing the significant bottleneck in autoformalization research: the scarcity of high-quality, parallel informal-formal data. Instead of relying on expensive manual curation, the authors leverage a powerful LLM (GPT-4) to translate existing large formal corpora (Isabelle’s Archive of Formal Proofs and Lean4’s mathlib4) into informal natural language. This innovative approach exploits the observation that informalization is significantly easier than formalization. The resulting MMA dataset comprises 332K multi-language, multi-domain informal-formal pairs, representing a large-scale and diverse resource for training and evaluating autoformalization models. The multi-lingual aspect of MMA is particularly noteworthy, offering the potential for improved generalization and cross-lingual transfer learning. This approach tackles data scarcity, providing a significantly larger and more flexible dataset than previously available, making it a valuable asset for advancing the field of autoformalization.

LLM Fine-tuning

#

LLM fine-tuning in the context of autoformalization focuses on adapting large language models to the specific task of translating informal mathematical statements into formal, machine-verifiable representations. The effectiveness of this approach hinges on the quality and quantity of the training data. A key challenge addressed is data scarcity, as manually creating paired informal-formal examples is expensive and time-consuming. The paper proposes a novel approach: using an LLM to translate from formal to informal, thus creating a larger and more easily generated dataset. This reverse translation leverages the inherent strengths of LLMs at generating natural language, overcoming the bottleneck of human annotation. The results demonstrate that models fine-tuned with this data achieve higher accuracy in autoformalization compared to models trained only with traditional few-shot learning, indicating that using large-scale, multi-lingual data can significantly boost the effectiveness of LLMs in this complex and challenging domain. This study highlights the power of data augmentation techniques for improving the performance of LLMs in specialized fields. The use of multiple formal languages also enhances the generalizability and robustness of the resulting model. Further research could explore the influence of different LLM architectures and the optimal balance between data size and model complexity.

Autoformalization Metrics

#

Autoformalization, the process of converting natural language mathematical statements into machine-verifiable formal languages, necessitates robust evaluation metrics. Simple metrics like accuracy (percentage of correctly formalized statements) are insufficient, as they don’t capture the nuances of formal language. A more informative metric is edit distance, measuring the number of changes needed to transform a generated formalization into a correct one. This accounts for near-misses, common in autoformalization. Beyond string-based metrics, assessing the semantic equivalence between informal and formal representations is crucial. This might involve comparing the theorems’ logical consequences or their interpretations. Computational cost should also be considered; an efficient autoformalization system shouldn’t demand excessive resources. Finally, evaluating the usefulness of the generated formalization in downstream tasks, such as automated theorem proving, offers a practical assessment of its quality. A holistic approach requires a combined assessment of accuracy, semantic similarity, computational efficiency, and practical utility to comprehensively evaluate autoformalization methods.

Future Directions

#

Future research could explore several promising avenues. Improving the accuracy and efficiency of informalization is crucial, perhaps by training larger language models on a more diverse corpus or incorporating techniques from symbolic AI. Expanding the scope of formal languages included in the dataset is also important, ensuring that the model can handle various mathematical domains. This might involve incorporating less widely-used proof assistants. Investigating the interplay between multi-language training and autoformalization performance warrants further investigation; does multi-language training generalize better than single-language, and can we quantify the benefits? Additionally, research into ways to evaluate formalizations automatically would improve the efficiency of the evaluation process and reduce the need for manual human expert assessment. Finally, exploring applications of this research to other fields such as automated theorem proving, code generation, and digital education is worth considering. Addressing these research directions will improve the tools and techniques available for automatically translating informal mathematical statements into machine-verifiable forms.

More visual insights

#

More on figures

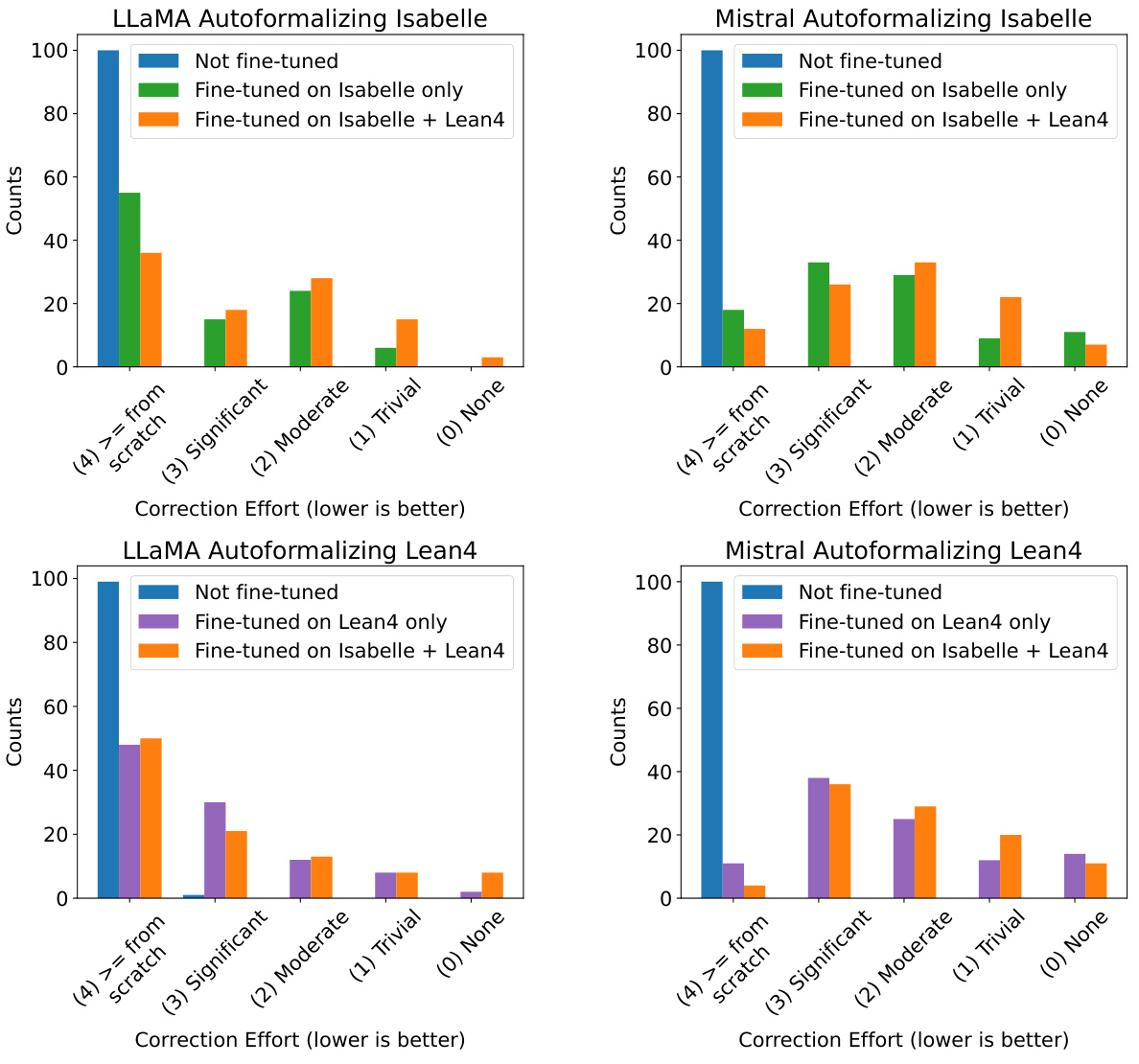
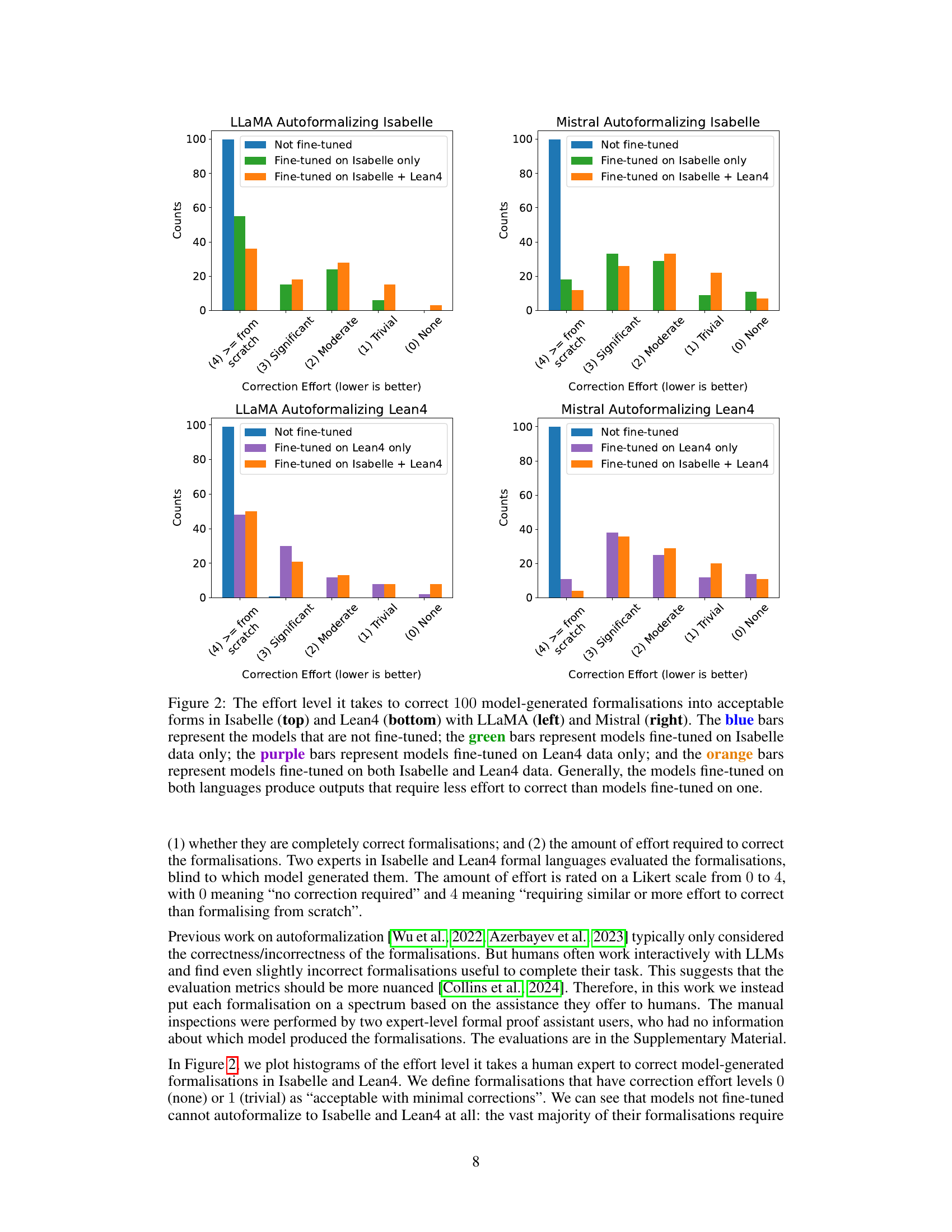
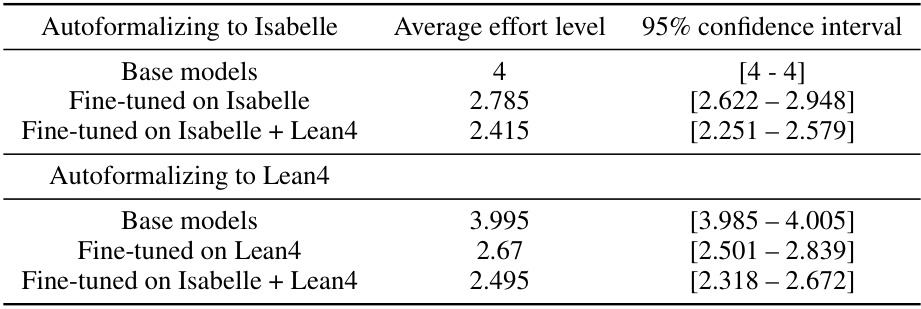
This figure shows the effort required to correct 100 model-generated formalizations in Isabelle and Lean4 for four different model training scenarios: no fine-tuning, fine-tuning on Isabelle only, fine-tuning on Lean4 only, and fine-tuning on both Isabelle and Lean4. The results are displayed using bar charts, separated by model (LLaMA and Mistral) and formal language (Isabelle and Lean4). The chart demonstrates that models fine-tuned on both languages generally require less effort to correct.

This figure shows the training curves for LLaMA model fine-tuned on different datasets: only Isabelle data, only Lean4 data, and both Isabelle and Lean4 data. The plots show both training loss and token accuracy. The results indicate that fine-tuning with data from multiple formal languages leads to lower validation loss and higher accuracy compared to using data from a single formal language.

This figure shows the training curves of three models fine-tuned on different datasets. The x-axis represents the training steps, while the y-axis shows the loss and token accuracy on the Isabelle and Lean4 validation sets. The results indicate that fine-tuning on both Isabelle and Lean4 datasets yields lower validation loss and higher accuracy than fine-tuning on only one dataset.

The figure shows the training curves for three different fine-tuning regimes on two language models. The x-axis represents the training steps, while the y-axis represents both the validation loss and token accuracy. The three regimes are: fine-tuning on Isabelle data only (green), fine-tuning on both Isabelle and Lean4 data (orange), and fine-tuning on Lean4 data only (purple). The results indicate that fine-tuning on multiple languages leads to lower validation loss and higher accuracy compared to single-language fine-tuning.

More on tables

The table presents statistics of the MMA dataset, including the number of data points, the average, median, minimum and maximum lengths of informal and formal statements. The bottom part shows the categorization of errors found in a manual evaluation of 200 randomly selected informal-formal pairs from the dataset, breaking down the error types.

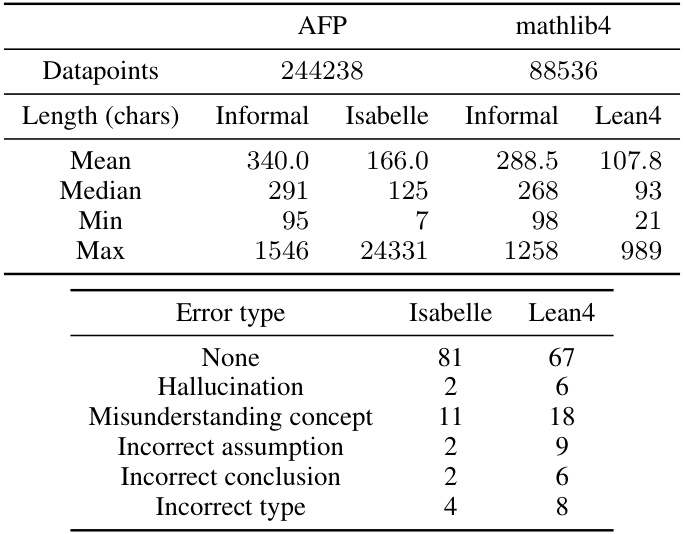
The table shows statistics of the MMA dataset, including the number of data points, the average, median, minimum, and maximum length of informal and formal statements in characters. The lower part shows the categorization of errors found in a manual evaluation of 200 informalized statements, indicating the frequency of different error types such as hallucination, misunderstanding concepts, incorrect assumptions, conclusions, and types.

This table presents a two-part statistical analysis of the MMA dataset. The top part displays statistics such as the number of data points, mean, median, min, and max character lengths of informal and formal statements (in Isabelle and Lean4). The bottom part shows the categorization of errors found in a manual evaluation of 200 randomly selected informal-formal pairs, classifying each error into categories like hallucination, misunderstanding of concepts, incorrect assumptions, etc.

Full paper

#