↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many real-world applications involve sequential learning where a system faces a series of related tasks. In the context of linear bandits, existing approaches often assume that these tasks are sufficiently diverse, which is often unrealistic. This assumption simplifies the problem, enabling the development of algorithms with strong theoretical guarantees. However, it limits the applicability of these algorithms to real-world scenarios where such an assumption doesn’t hold. This paper addresses this limitation by studying sequential multi-task linear bandits without the task diversity assumption.
The paper introduces a novel algorithm called BOSS (Bandit Online Subspace Selection) that tackles the challenges of sequential learning. BOSS utilizes a clever bi-level approach to address the problem. The algorithm learns a low-rank representation that captures the shared structure across tasks without assuming diversity. The paper also provides theoretical guarantees, establishing that the meta-regret of BOSS is significantly lower than previous methods under more general assumptions. The result is demonstrated empirically on synthetic data.
Key Takeaways#
Why does it matter?#
This paper is crucial because it addresses a critical limitation in multi-task linear bandit algorithms, enabling efficient lifelong learning without unrealistic assumptions about task diversity. This opens new avenues for research in various sequential learning scenarios and improves the practical applicability of existing methods.
Visual Insights#
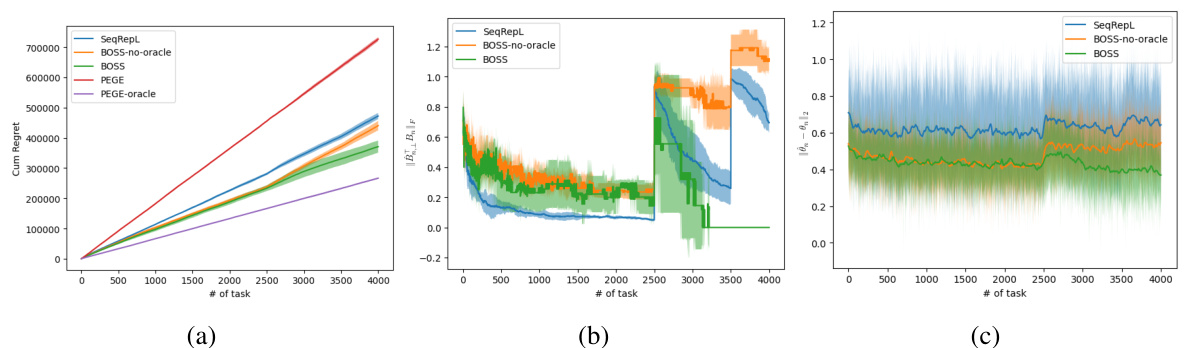
This figure compares the cumulative regret of five different algorithms: SeqRepL, BOSS-no-oracle, BOSS, PEGE, and PEGE-oracle. The experiment uses 4000 tasks, each with a horizon of 500, in a 10-dimensional space with a 3-dimensional subspace. Crucially, the subspace changes at tasks 1, 2501, and 3501, violating the task diversity assumption often made in similar research. The plot shows that BOSS and its variants significantly outperform the baselines (PEGE and SeqRepL), highlighting the algorithm’s effectiveness even without task diversity.
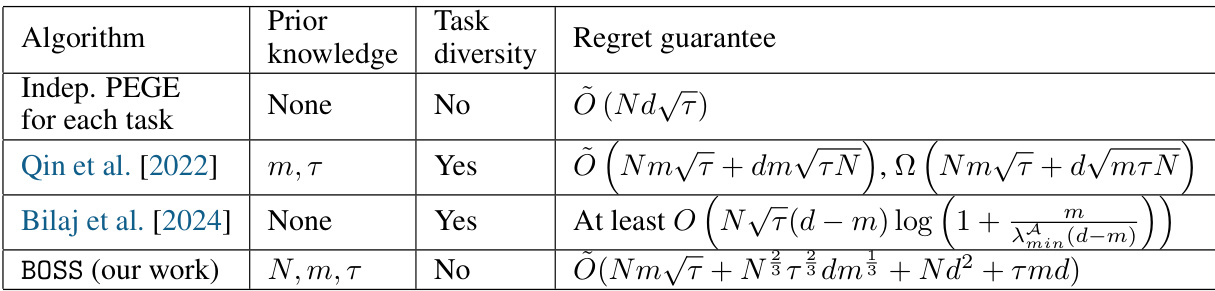
This table compares the regret guarantees of various algorithms for multi-task linear bandits. It contrasts the algorithms’ assumptions about prior knowledge of the task structure (low-rank subspace), the task diversity assumption (whether tasks are diverse or not), and the resulting regret bounds. The table highlights the improvement of the proposed algorithm (BOSS) over existing methods by relaxing the task diversity assumption while still maintaining a provable regret bound.
In-depth insights#
Lifelong Linear Bandits#
Lifelong linear bandits represent a significant area of research within the broader field of reinforcement learning. They address the challenge of creating learning agents that can adapt and improve their performance over an extended period of time, encountering a sequence of related yet distinct tasks. The “linear” aspect signifies that the reward function is modeled linearly using the agent’s actions and contextual information. A key focus is efficient transfer learning, where knowledge acquired from previous tasks is leveraged to expedite learning on new tasks, rather than treating each task in isolation. This approach addresses the impracticality of starting from scratch for each new task encountered. Central issues include effective exploration-exploitation strategies in a dynamic setting; to determine the balance between exploring new action-reward relationships and exploiting known effective actions. Another important aspect is robust algorithm design, that handles non-stationarity or variations in task characteristics, and provides theoretical performance guarantees. The development of provably efficient algorithms capable of robust representation transfer and lifelong learning in linear bandit settings would have broad implications to areas like recommendation systems and personalized decision-making systems. Successful algorithms should overcome challenges of diverse data distributions and effectively manage the trade-off between exploration and exploitation across multiple tasks to achieve high cumulative performance.
Low-Rank Transfer#
Low-rank transfer learning in the context of multi-task linear bandits focuses on leveraging shared structures across tasks to improve efficiency and reduce regret. The core idea is that when the parameters of multiple linear bandit tasks lie within a low-dimensional subspace of a high-dimensional space, a low-rank representation can capture the essential information. This allows for efficient transfer of knowledge learned from one task to others, rather than learning each task independently. Algorithms based on this approach aim to identify and utilize this shared low-rank structure, often using matrix factorization or similar techniques to learn a shared representation. A key challenge is to balance exploration (learning about the shared structure) and exploitation (using the learned structure to improve performance on new tasks). Success depends on the validity of the low-rank assumption and the algorithm’s capacity to accurately learn the shared subspace. Further research often addresses relaxing strong assumptions like task diversity, and developing more robust algorithms capable of handling non-ideal scenarios where the low-rank assumption might be only partially true.
BOSS Algorithm#
The BOSS algorithm, designed for sequential multi-task linear bandits, tackles the challenge of representation transfer learning without relying on the often-unrealistic task diversity assumption. Its core innovation lies in a bi-level approach: a lower level that balances exploration and exploitation within individual tasks using two base algorithms, and an upper level that dynamically selects between meta-exploration (learning the shared subspace) and meta-exploitation (leveraging the learned subspace). This approach efficiently learns and transfers low-rank representations, achieving a provable regret bound. Unlike prior methods, BOSS’s theoretical guarantees are robust to task parameter variations, making it particularly suited for real-world scenarios where tasks may not uniformly span the subspace. Random meta-exploration helps BOSS overcome the challenge of uncertainty about the shared subspace structure, allowing it to adapt effectively to different levels of task diversity. The algorithm’s empirical performance on synthetic data showcases its superiority over baseline methods, highlighting its efficacy in scenarios where task diversity is absent or violated.
Meta-Exploration#
In the context of multi-task linear bandits, meta-exploration is a crucial concept that addresses the challenge of learning a shared low-rank representation across multiple tasks without strong assumptions like task diversity. It acknowledges the inherent uncertainty about the underlying structure and proposes strategies to actively discover this structure through strategic exploration. Unlike traditional exploration within individual tasks, meta-exploration focuses on gaining information about the shared subspace, which enables effective transfer learning across tasks. This typically involves a carefully designed balance between exploring the full action space to estimate individual task parameters and exploring a reduced subspace, guided by an estimate of the shared low-rank representation. Efficient meta-exploration is key to achieving low meta-regret—the cumulative regret across all tasks—and often relies on novel algorithms that adaptively allocate exploration resources between individual task exploration and the higher-level task of learning the shared structure. The effectiveness of meta-exploration is inherently linked to the assumption made regarding the shared representation and the presence or absence of task diversity.
Future Work#
The ‘Future Work’ section of this research paper presents exciting avenues for extending the current study on sequential representation transfer in multi-task linear bandits. Addressing the limitations of relying on strong assumptions, like the task diversity assumption, is crucial. The authors rightly acknowledge the need to develop algorithms that perform comparably to individual single-task baselines across a wider range of parameter settings. This necessitates improved theoretical bounds and likely more sophisticated meta-exploration techniques. Extending the algorithm’s applicability to general action spaces and time-varying action spaces is a key challenge. Finally, enhancing the computational efficiency of the proposed algorithm (BOSS) is necessary, especially considering the exponentially large expert set used. Addressing these points will improve the algorithm’s practical usability and strengthen its theoretical foundation.
More visual insights#
More on figures

This figure compares the cumulative regret of the BOSS algorithm with four baselines: SeqRepL, PEGE, PEGE-oracle, and BOSS-no-oracle. The experiment settings are N=4000 tasks, T=500 rounds per task, d=10 dimensions, and m=3 subspace dimensions. The reward vectors θn are chosen uniformly at random, ensuring their l2 norm is between 0.8 and 1. The environment changes the underlying subspace at tasks 1, 2501 and 3501, simulating a non-stationary environment without task diversity. The plot shows that BOSS consistently outperforms the baselines, highlighting the effectiveness of its approach in learning low-rank representations without task diversity.
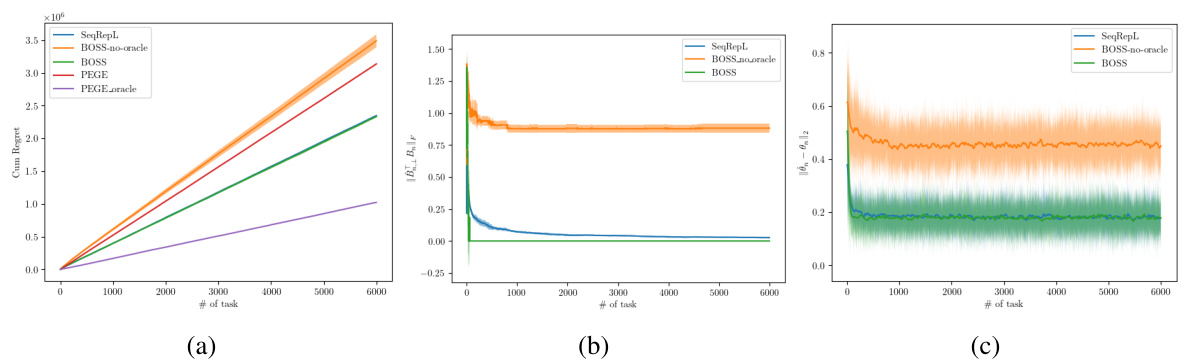
This figure compares the cumulative regret of four algorithms: BOSS, BOSS without oracle knowledge, SeqRepL, and PEGE. The experiment uses 6000 tasks with a horizon of 2000 rounds each. The dimensionality of the tasks is 10, and the subspace dimension is 3. The figure shows that BOSS outperforms the other algorithms, particularly when the task diversity assumption holds. The plots also display metrics related to the subspace basis estimation error.
Full paper#