↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Replicable machine learning algorithms, which produce consistent results despite variations in input data, are highly sought after. However, designing such algorithms is often challenging due to their increased sample and list complexities. This paper investigates this problem using geometric partitions and variants of Sperner’s Lemma, which provides a geometric approach to algorithm design and analysis. Existing research utilizes these tools, but leaves open questions about the optimality of such techniques and their limitations.
The study reveals the near-optimality of previous work, showing that existing algorithms are nearly as efficient as possible. Furthermore, this paper provides a new construction of secluded partitions with improved tolerance parameters. It presents a novel ’neighborhood’ variation of Sperner’s Lemma, offering a more nuanced understanding of geometric properties and their implications for replicable learning. This enhances the current toolbox for designing and analyzing such algorithms.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on replicable learning algorithms. It provides novel insights into the connection between geometry and replicability, offering improved techniques for designing algorithms with low list and sample complexities. The new neighborhood variant of Sperner/KKM lemma opens avenues for further research in various fields.
Visual Insights#
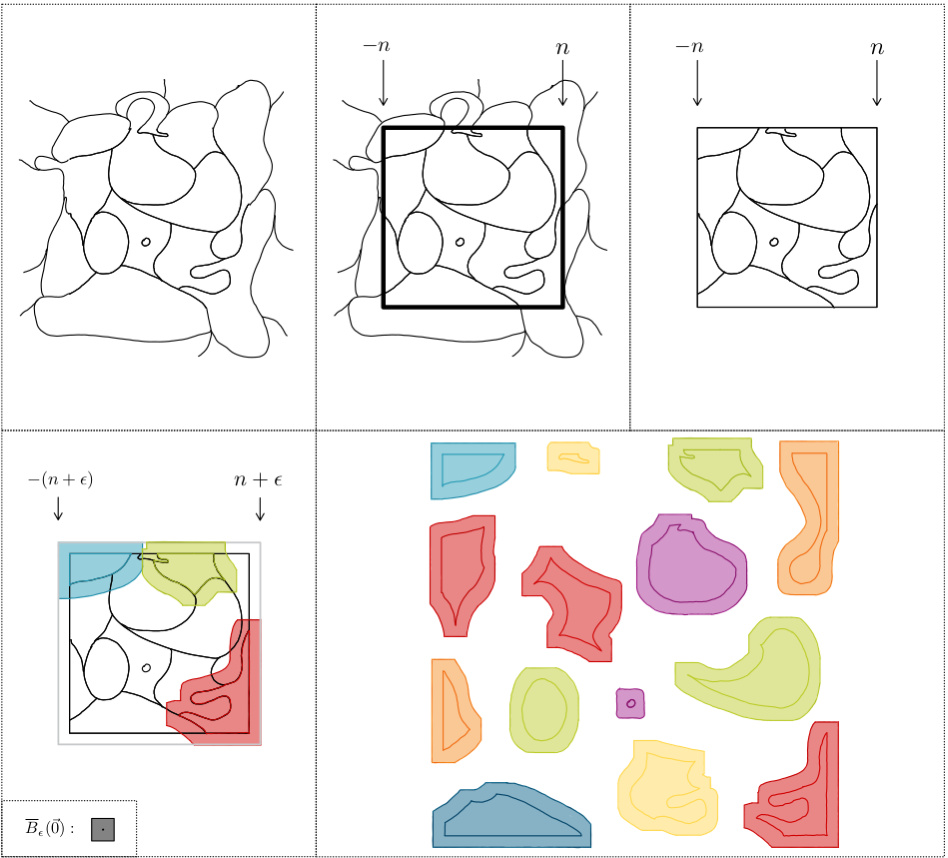
This figure visually depicts the steps involved in proving Theorem 3.1. It demonstrates how the measure of the Minkowski sum of enlarged partition members surpasses the measure of a larger bounding box by a significant factor. This leads to the conclusion that certain points must be covered by many members of the enlarged partition. This illustrates the core of the proof.
Full paper#



















