↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Existing contextual multinomial logit (MNL) bandit models are limited by their reliance on (generalized) linear value functions. This significantly restricts their applicability to real-world assortment recommendation problems where complex relationships exist between customer choices, item valuations, and contextual factors. The paper highlights this issue, and proposes to overcome it by developing more sophisticated models.
This paper addresses this issue by introducing contextual MNL bandit models that utilize general value functions. The researchers propose a suite of novel algorithms tailored for both stochastic and adversarial contexts, demonstrating superior performance compared to existing methods. Key improvements include dimension-free regret bounds and the ability to manage completely adversarial contexts and rewards, representing a substantial advancement in the field.
Key Takeaways#
Why does it matter?#
This paper is crucial because it addresses the limitations of existing contextual MNL bandit models by incorporating general value functions. This opens new avenues for research in assortment recommendation, offering improved accuracy and applicability to real-world scenarios. The dimension-free regret bounds and ability to handle completely adversarial contexts are significant advancements.
Visual Insights#
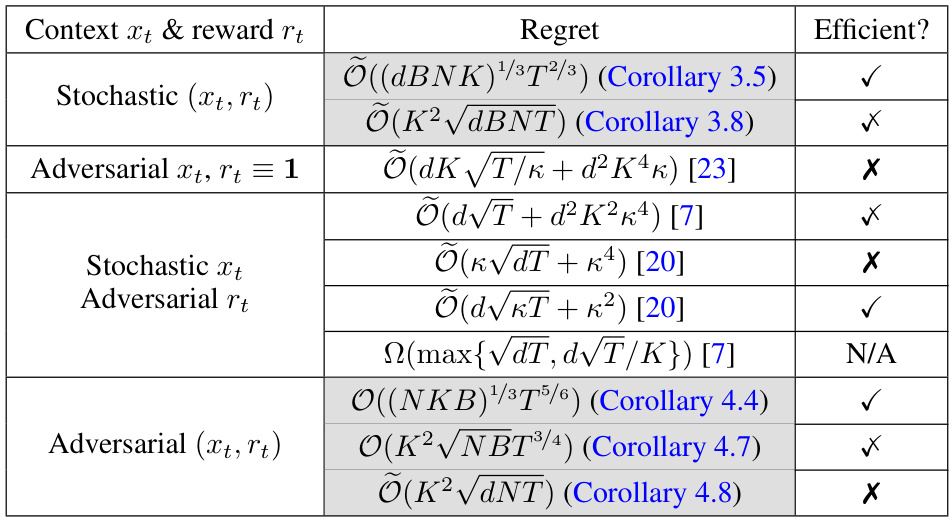
This table compares the regret bounds and computational efficiency of various algorithms for contextual multinomial logit (MNL) bandits with linear value functions. It highlights the dependence (or lack thereof) on a problem-dependent constant κ, which can be exponentially large. The algorithms are categorized by the setting (stochastic or adversarial) and the type of feedback available (context and reward, context only, or reward only). The ‘Efficient?’ column indicates whether the algorithm’s runtime is polynomial in all parameters, polynomial only for constant K, or non-polynomial.
Full paper#