↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many online services cannot directly A/B test due to business constraints. Instead, they use encouragement designs, but comparing treatment and control groups based on self-selection can lead to biased results. This study addresses this “confounded pure exploration” problem, which arises when user engagement is influenced by unobserved factors related to treatment response.
The paper proposes a novel approach using transductive linear bandits and encouragement designs, formulated as the CPET-LB problem. It introduces elimination-style algorithms that adapt to the confounded data, incorporating a new finite-time confidence interval to estimate treatment effects. The researchers provide theoretical guarantees on sample complexity, showing that their method achieves performance close to the theoretical optimum, and demonstrate efficacy via experimental results.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in online services and causal inference because it addresses the critical issue of confounding in A/B testing. It offers a novel methodology for adaptive experimentation when direct randomization isn’t feasible, presenting valuable algorithms and theoretical guarantees. The findings are particularly relevant to those working with encouragement designs and instrumental variables, broadening the scope of effective online experimentation.
Visual Insights#

The figure shows a causal graph representing the relationship between encouragement (Z), user choice (X), outcome (Y), and confounder (U). An arrow indicates a direct causal effect. The confounder (U) affects both user choice and outcome, representing unobserved factors influencing a user’s decision and the final result. The encouragement design incentivizes users toward a specific treatment, influencing user choice, but not directly causing the outcome (only indirectly through user choice). This setup highlights the challenges of potential confounding in evaluating treatment effects.

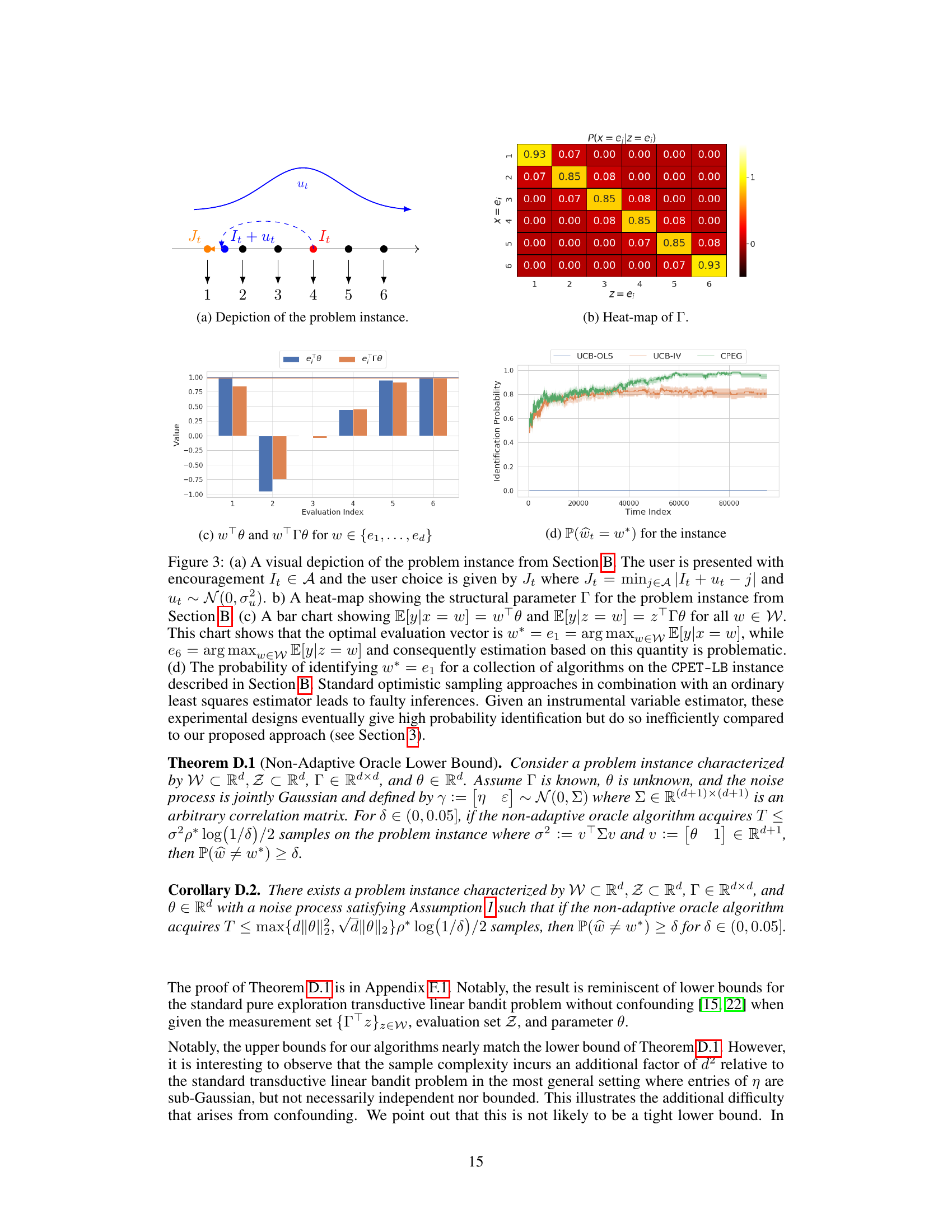
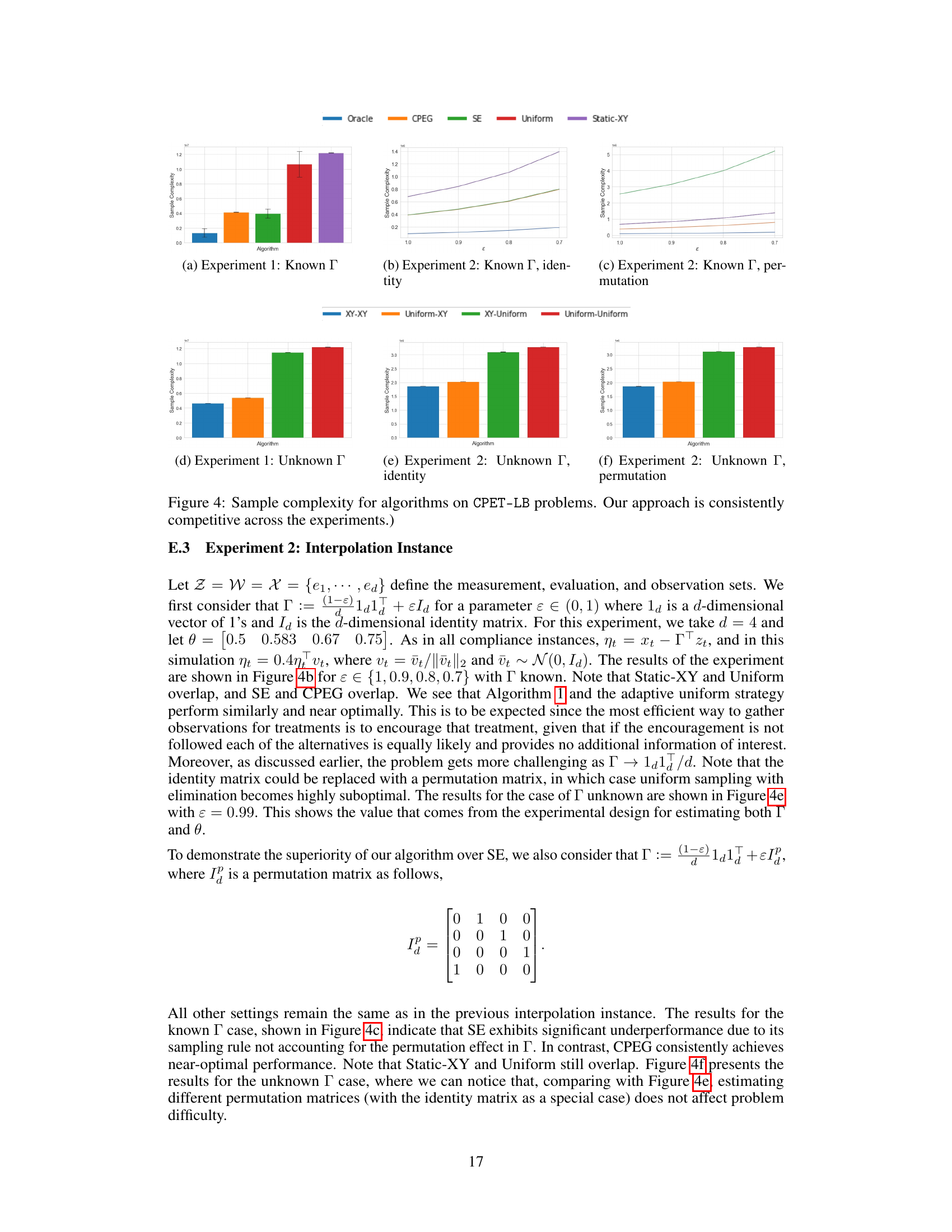
This figure presents the sample complexity results for different algorithms tackling the Confounded Pure Exploration Transductive Linear Bandit (CPET-LB) problem, categorized by whether the structural model parameter Γ is known or unknown. The algorithms are compared across different experimental settings, including a ‘Jump-Around’ instance and an ‘Interpolation’ instance. The results demonstrate the effectiveness of the proposed CPEG algorithm in achieving consistently competitive sample complexity compared to baseline methods, irrespective of whether Γ is known or not. The chart visually represents the sample complexity, providing a clear comparison of performance across various scenarios.
In-depth insights#
Confounded Bandits#
Confounded bandits address a crucial challenge in reinforcement learning where the reward a learning agent receives is influenced by hidden, unobserved factors, leading to biased estimations of action values. The core issue is that the observed reward doesn’t solely reflect the action taken but also these confounding variables. This makes it difficult to accurately assess the true effectiveness of different actions. Solutions involve advanced statistical techniques like instrumental variables or causal inference to disentangle the effects of actions from confounders, enabling a more robust learning process. Successfully addressing confounding in bandits is paramount for reliable decision-making in real-world applications, where uncontrolled factors significantly impact outcomes. Research in this area is actively exploring various methods to effectively handle confounding, improving the accuracy and reliability of bandit algorithms in complex environments.
Adaptive Designs#
Adaptive experimental designs are crucial for efficient and effective research, particularly in scenarios with limited resources or high uncertainty. Adaptive designs allow researchers to modify the experimental protocol based on accumulating data, enabling optimized data collection and resource allocation. This approach contrasts with traditional fixed designs, where the experimental plan remains unchanged regardless of observed results. A key advantage is the ability to dynamically adjust sample sizes, focusing resources on the most promising treatments or conditions. This reduces the overall sample size required, leading to cost savings and faster insights. However, careful consideration of ethical implications, the potential for bias, and the complexity of analysis are essential aspects when implementing adaptive designs. The choice of an appropriate adaptive design depends on the research question, the characteristics of the data, and available resources, demonstrating the need for a thoughtful and in-depth approach to maximize its benefits.
2SLS Estimators#
Two-Stage Least Squares (2SLS) estimators are a crucial statistical technique for addressing endogeneity in causal inference, particularly relevant when dealing with observational data. 2SLS is especially useful when a direct causal relationship between an independent and dependent variable is confounded by omitted variables or simultaneity. The approach leverages an instrumental variable (IV) that is correlated with the independent variable but not directly with the dependent variable, creating a two-stage estimation process. The first stage regresses the endogenous independent variable on the IV and other relevant controls, obtaining predicted values. These predicted values are then used in the second stage to estimate the causal effect, mitigating the bias introduced by endogeneity. A key assumption for valid 2SLS is the exclusion restriction: the IV only affects the dependent variable through its influence on the independent variable. Violation of this assumption can lead to biased estimates. Furthermore, weak instruments (IVs weakly correlated with the independent variable) can result in imprecise 2SLS estimates. Therefore, careful consideration of instrument relevance and strength is necessary. Finally, the reliability of 2SLS hinges on correct model specification, and misspecification can compromise the validity of causal inferences. Researchers should conduct diagnostic tests to assess the robustness of their 2SLS estimates.
Sample Complexity#
Sample complexity analysis in machine learning research is crucial for evaluating the efficiency of algorithms. It quantifies the number of samples an algorithm needs to achieve a desired level of accuracy or performance. In the context of adaptive experimental designs, such as those used in bandit problems, sample complexity becomes particularly important, as the algorithm actively learns and adapts based on the acquired data. Lower bounds on sample complexity provide theoretical limits, establishing the minimum number of samples any algorithm requires to succeed. Upper bounds, derived through analysis of specific algorithms, indicate the actual sample complexity. A good algorithm aims to have upper bounds that are close to the lower bounds. The paper likely investigates how factors like confounding, encouragement designs, and the choice of sampling methods influence the sample complexity of algorithms for learning treatment effects in online services. The authors probably prove theoretical guarantees on the sample complexity of their proposed algorithm, comparing it to existing approaches. Tight upper bounds, which closely match the lower bounds, would demonstrate the algorithm’s efficiency and near-optimality.
Future Directions#
Future research could explore several promising avenues. Extending the CPET-LB framework to handle more complex confounding structures is crucial, moving beyond the linear structural equation model. Investigating settings with non-linear relationships between variables or time-varying confounders would significantly enhance the model’s real-world applicability. Additionally, developing more efficient algorithms for the CPET-LB problem, possibly through improved experimental design techniques or advanced bandit algorithms, is a key area for future work. The theoretical findings could be validated through extensive simulations under diverse scenarios and conditions that mimic real-world challenges faced by online services. Empirical studies on various online services with encouragement designs are necessary to demonstrate the practical utility of the proposed methodology. Finally, exploring applications in other fields where pure exploration with confounding is prevalent, such as healthcare or social sciences, holds great potential.
More visual insights#
More on figures

This figure compares the performance of several algorithms for identifying the optimal treatment in a confounded pure exploration setting. Panel (a) illustrates the difference between the true optimal treatment (w*) and the naive estimate based on the observed encouragement (z). Panel (b) shows the success rate of these algorithms in correctly identifying w* over time.
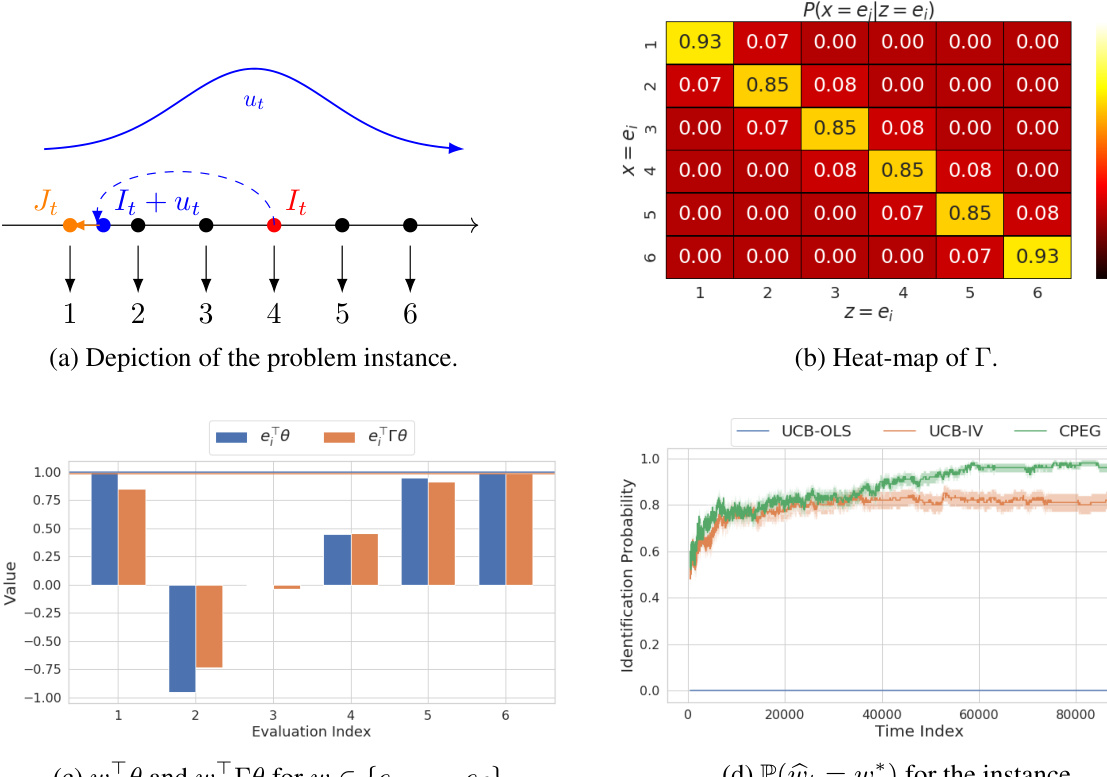
This figure shows the setup of a compliance example in which users have hidden preferences and choose to engage with treatments based on incentives. Subfigures (a) and (b) illustrate the model, while (c) and (d) contrast naive approaches with the authors’ proposed method.

This figure presents a comparison of different algorithms for solving the CPET-LB problem. The left panel shows the expected reward for each treatment option given either the user’s choice (x) or the encouragement (z). The right panel shows the probability of each algorithm correctly identifying the optimal treatment (w*) over 100 simulations. This highlights the bias introduced by using the encouragement (z) without accounting for confounding and the effectiveness of the proposed method (CPEG).
Full paper#