↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Generative modeling of time series data faces challenges in handling varying sequence lengths, with existing methods often designed for either short or long sequences. This dichotomy is mainly due to gradient issues in recurrent networks, computational costs in transformers, and limited expressiveness in state space models. The limitations of these existing methods hinder their ability to generate high-quality samples for time series data of various lengths. A unified framework is needed to address this challenge and produce high-quality time series of varying lengths effectively.
ImagenTime tackles this problem by transforming time series data into images via invertible transforms (delay embedding and short-time Fourier transform). This image representation allows leveraging the power of advanced diffusion models designed for image data. The method demonstrates superior performance on various tasks, including unconditional generation, interpolation, and extrapolation, across multiple datasets with varying sequence lengths. This approach consistently achieves state-of-the-art results, highlighting its effectiveness and versatility in generative modeling of time series data.
Key Takeaways#
Why does it matter?#
This paper is important because it presents a novel unified framework for generative modeling of time series data, addressing the limitations of existing approaches that struggle with varying sequence lengths. It achieves state-of-the-art results on various benchmarks, opening new avenues for research in this field and offering a versatile tool for researchers working with sequential data.
Visual Insights#

This figure illustrates the training and inference pipeline of the proposed ImagenTime framework. During training, a time series is first transformed into an image representation using a chosen invertible transform (like delay embedding or STFT). Noise is added to this image, and a U-Net based diffusion model is trained to remove this noise and reconstruct a clean image. The clean image is then inversely transformed back into a time series. During inference, the process is reversed: the diffusion model generates a clean image from random noise, and this image is then inversely transformed to produce a new, generated time series.
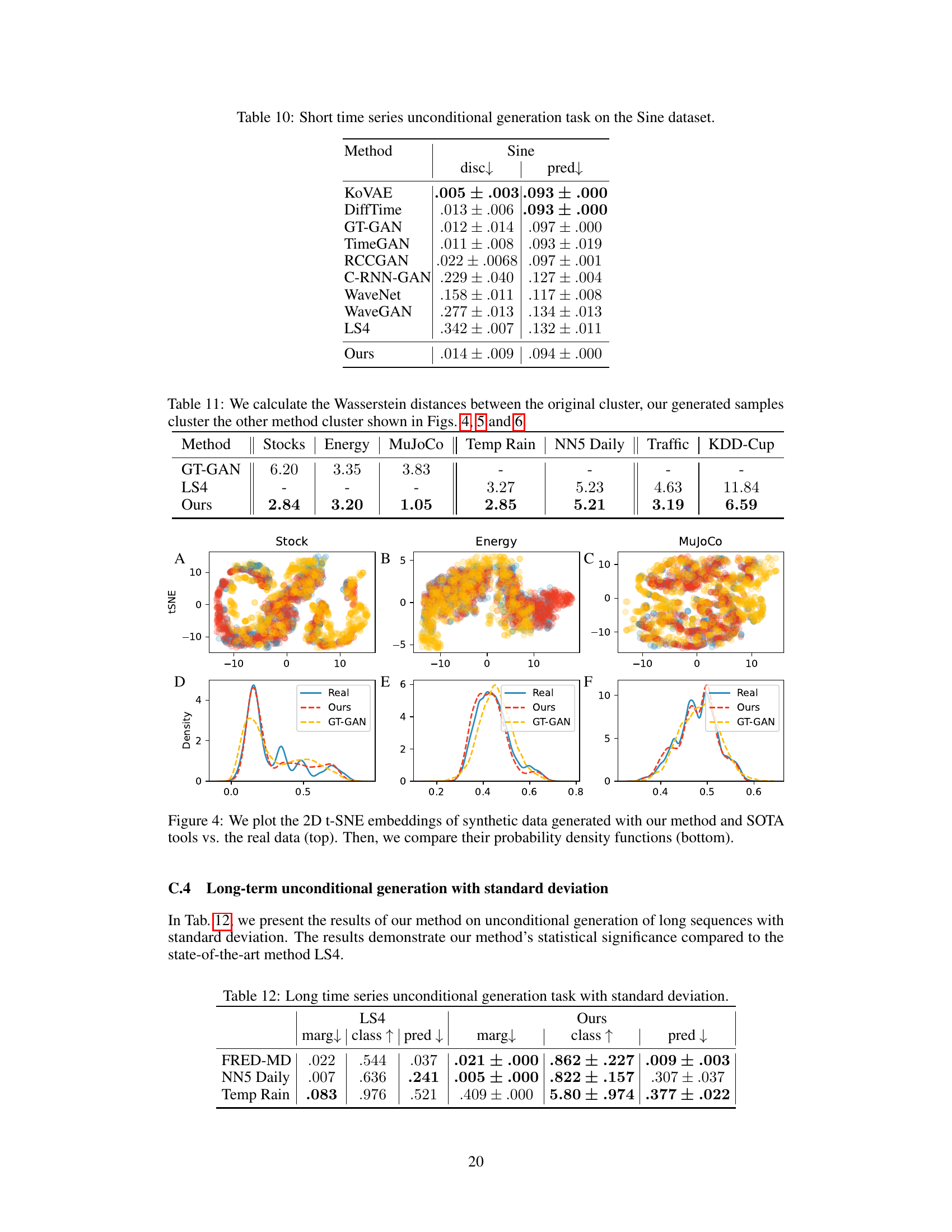
This table presents the performance of various generative models on short time series data for unconditional generation tasks. It uses two metrics: discriminative score (disc↓) and predictive score (pred↓). Lower scores indicate better performance. The datasets used are Stocks, Energy, and MuJoCo, representing different characteristics of time-series data. The ‘Ours’ row shows the performance of the proposed method in this paper, which consistently outperforms the existing methods.
In-depth insights#
Time Series to Images#
Transforming time series data into images is a powerful technique for leveraging the strengths of computer vision. This approach bypasses the limitations of traditional time series models by representing temporal data in a spatial format more easily processed by convolutional neural networks. Several methods exist for this conversion, each with advantages and drawbacks. Delay embedding preserves temporal relationships but can be computationally expensive for long sequences. Short-Time Fourier Transform (STFT) captures frequency information over time, ideal for data with strong periodic components, but might lose some temporal resolution. The choice of transformation depends on the specific characteristics of the data and the downstream tasks. The successful application of this technique relies on selecting an appropriate transformation method, carefully considering potential information loss during conversion, and ensuring the chosen method is invertible for data reconstruction if needed. Ultimately, this image-based approach opens up new possibilities for generative modeling, classification, and other analyses of time series data.
Diffusion Models#
Diffusion models, a class of generative models, have gained significant traction due to their ability to generate high-quality samples from complex data distributions. They work by gradually adding noise to data until it becomes pure noise, then learning a reverse diffusion process to reconstruct the original data. This approach avoids the common pitfalls of other generative models, such as mode collapse and training instability. A key strength is the capacity to generate diverse and high-fidelity samples, surpassing traditional methods. The framework’s mathematical elegance and intuitive nature make them highly appealing. However, the computational cost of sampling from diffusion models can be substantial, requiring many iterative steps. Recent research focuses on improving sampling efficiency and broadening applicability. While initially applied to images, diffusion models are increasingly used in audio and other domains, suggesting a wide scope of potential applications and continued evolution.
Generative Modeling#
Generative modeling, in the context of time series, presents a significant challenge due to the inherent complexities of sequential data. Existing methods often struggle with either short or long sequences, failing to provide a unified approach. This limitation stems from issues such as vanishing gradients in recurrent networks, computational costs with transformers, and the limited expressiveness of state-space models. The use of image transforms offers a compelling solution, mapping time series data into image representations. This transformation allows leveraging the power and advancements of diffusion models developed for image generation, a field with considerably more mature techniques. This approach’s key advantage lies in its ability to handle both short and long time series within the same framework, overcoming the limitations of traditional sequence modeling methods. The success of this approach depends on the choice of suitable invertible transforms that preserve essential temporal information, and careful consideration of the architectural design of the diffusion model itself. Further research should investigate the optimal transform selection for different types of time series data and explore the potential of other generative models in this context.
Experimental Results#
A robust ‘Experimental Results’ section would meticulously detail the datasets used, clearly outlining their characteristics and limitations. It would then present the chosen evaluation metrics, justifying their relevance to the research question. The results themselves should be presented with clarity and precision, using tables and figures effectively to highlight key findings. Statistical significance should be explicitly stated, possibly using error bars or p-values, to support the claims made. A discussion of both qualitative and quantitative results would provide a comprehensive view, potentially including failure cases or unexpected outcomes. Finally, a comparison to relevant baselines is crucial to demonstrate the novelty and impact of the proposed approach. Ablation studies, systematically removing or modifying elements, can bolster confidence in the results by isolating the contribution of each component. By addressing all these elements, the ‘Experimental Results’ section could offer a compelling and trustworthy account of the research.
Future Directions#
Future research could explore more sophisticated time-series-to-image transformations, potentially leveraging deep learning techniques to learn optimal mappings tailored to specific data characteristics. Investigating alternative diffusion models beyond those currently employed, such as exploring more efficient or robust architectures, is also warranted. A key area for development involves handling high-dimensional and irregularly sampled time series more effectively; current methods often struggle with such data. Finally, expanding the scope to conditional generation tasks beyond interpolation and extrapolation, such as anomaly detection or forecasting under uncertainty, would significantly broaden the applicability of image-based diffusion models in time series analysis. The development of more robust evaluation metrics that go beyond simple reconstruction error and account for the temporal dynamics of the data would also help to more accurately assess the quality of the generated sequences. Addressing the issue of scalability to ultra-long sequences in a computationally feasible way remains an important direction.
More visual insights#
More on figures
This figure shows four different image transformations applied to a sample time series signal. Panel (A) displays the raw time series data. Panels (B), (C), and (D) illustrate how the Gramian Angular Field, the Short Time Fourier Transform (STFT), and the Delay Embedding method, respectively, transform the one-dimensional time series into a two-dimensional image representation. Each transformation has different properties and advantages for processing time series data. The figure serves to illustrate the various image-based representations used to input the data into the proposed generative model.

This figure shows four different representations of the same time series data. The first panel (A) displays the original time series as a line graph. The following three panels illustrate three different image transformations of this time series data: Gramian Angular Field, Short Time Fourier Transform (STFT), and Delay Embedding. Each image transformation provides a distinct visual representation of the time series, highlighting different aspects of its structure and characteristics. These transformations are crucial for applying computer vision techniques to time series data for tasks like generative modeling.

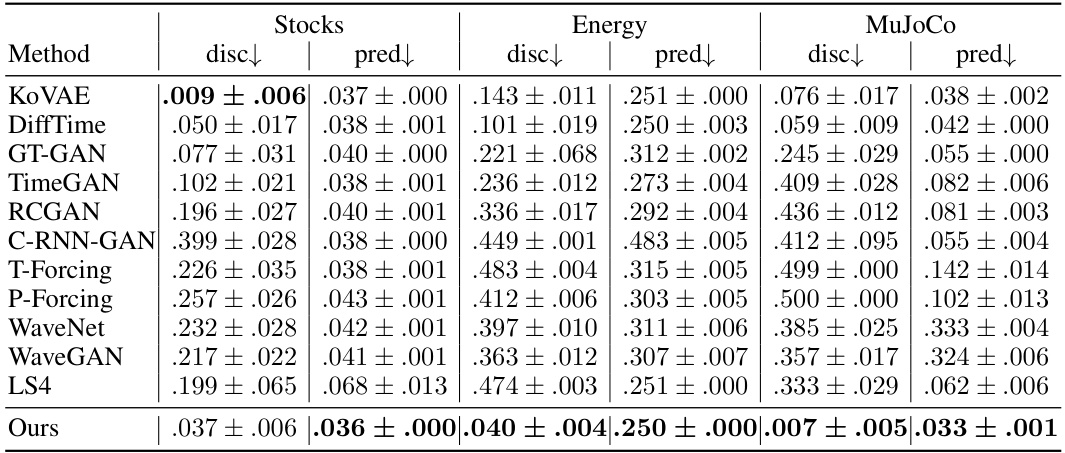
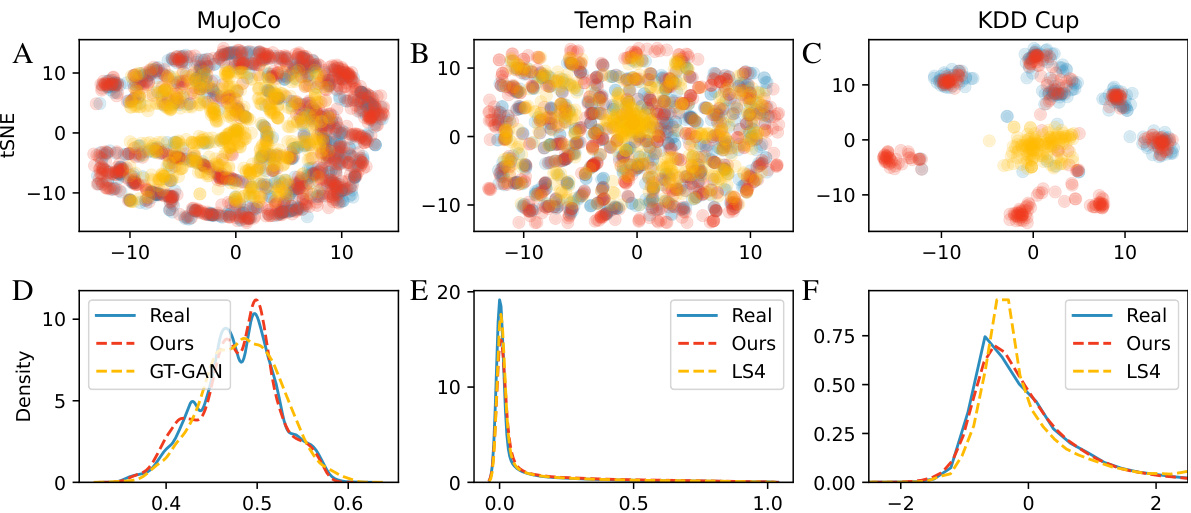
This figure presents a comparison of the results obtained using the proposed method against state-of-the-art (SOTA) techniques. The top row displays 2D t-SNE embeddings, visualizing how well the generated data (from both the proposed method and SOTA methods) aligns with the real data distribution. The bottom row shows the probability density functions of the generated and real data, offering a more detailed view of the similarity between the generated and real data distributions.
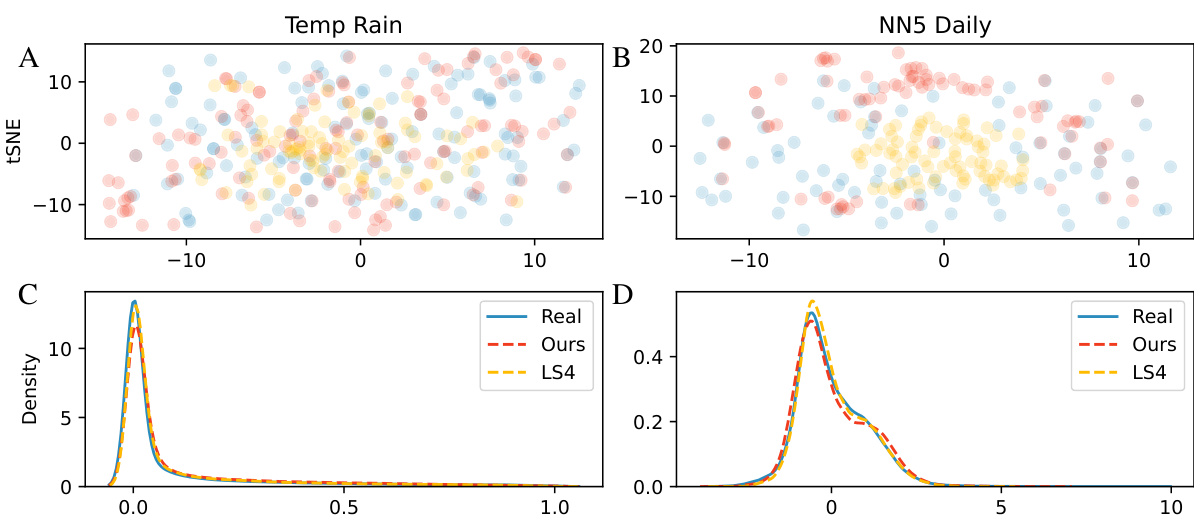
This figure shows a comparison of the generated data from the proposed method and other state-of-the-art methods against real data. The top row presents 2D t-SNE embeddings to visualize the data distribution, where similar data points are grouped together. The bottom row shows the probability density functions (PDFs) for each dataset, providing a detailed view of the data distribution characteristics. By visually comparing the embeddings and PDFs, one can assess how well the generated data resembles the real data and the differences between the proposed approach and other methods.

This figure shows four different image representations of the same time series data. Panel (A) displays the original time series as a line graph. The remaining panels (B, C, and D) illustrate three different image transformations applied to the time series: the Gramian angular field, the short-time Fourier transform, and delay embedding, respectively. These image representations can be used as inputs for vision-based diffusion models. Each method for converting a time series to an image captures different aspects of the time series’ temporal structure and frequency characteristics. The visualization helps to understand how various transformations can be employed before processing the data with image-based models.

This figure presents a scaling law analysis for three different time series generative models: DiffTime, LS4, and the authors’ proposed model, which leverages image transformations and diffusion models. The x-axis represents the number of model parameters (in millions), and the y-axis represents the discriminative score, a measure of how well the generated data resembles real data (lower is better). Error bars indicate standard deviation. The figure demonstrates how the discriminative score changes as the model size increases for each method. The goal is to assess whether increasing model complexity consistently leads to improved performance.
More on tables
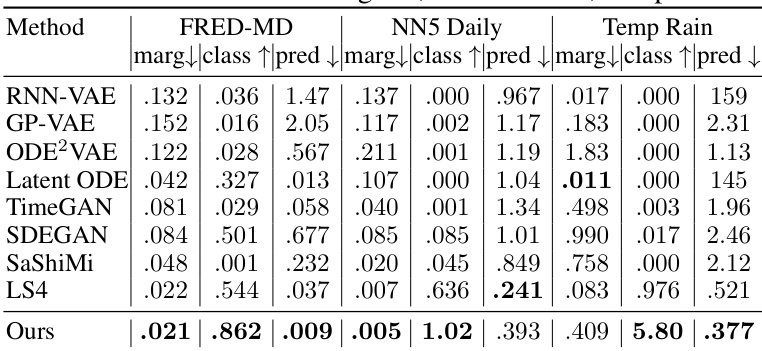
This table presents the results of the long-term unconditional generation experiments. It compares the performance of the proposed method against several state-of-the-art baselines across three real-world datasets: FRED-MD, NN5 Daily, and Temperature Rain. The evaluation metrics include marginal likelihood, classification accuracy, and prediction accuracy. Each metric provides a quantitative assessment of how well each method captures the underlying data distribution and generates realistic time series samples.
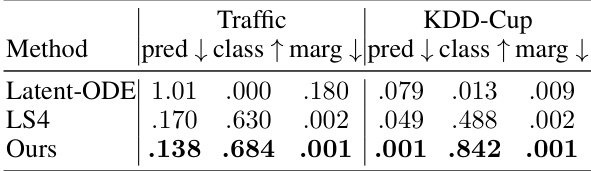
This table presents the results of ultra-long unconditional generation experiments on two datasets: Traffic and KDD-Cup. The results are compared across three metrics: prediction (pred), classification (class), and marginal (marg). Lower values for prediction and marginal indicate better performance, while higher values for classification suggest that the generated samples are more difficult to distinguish from real samples. The table compares the performance of three methods: Latent-ODE, LS4, and the proposed ‘Ours’ method.

This table presents the results of interpolation and extrapolation experiments on various time-series datasets with varying lengths. It compares the performance of several generative models, including ODE-RNN, Latent ODE, CRU, LS4, and the proposed ‘Ours’ method, in terms of mean squared error (MSE). Lower MSE values indicate better performance. The asterisk (*) indicates that the LS4 and CRU models did not converge for the Traffic and KDD-Cup datasets within seven days of runtime.

This table presents the performance of various generative models on short time series data for unconditional generation tasks. It compares the results on three datasets (Stocks, Energy, MuJoCo) across two metrics: discriminative score (disc↓) and predictive score (pred↓). Lower scores indicate better performance. The ‘disc’ metric uses a discriminator to assess how well the generated data resembles the real data, while ‘pred’ evaluates the predictability of the generated sequences using a separate prediction model.
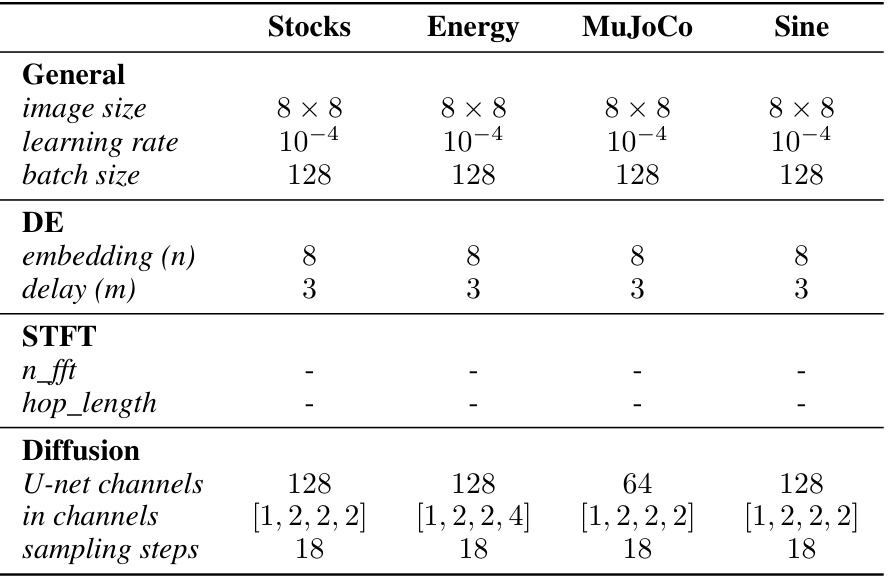
This table lists the hyperparameters used for the short-term unconditional generation experiments. It breaks down the parameters into three categories: General (image size, learning rate, batch size), Delay Embedding (embedding (n), delay (m)), and Short Time Fourier Transform (n_fft, hop_length). The final section covers Diffusion model parameters (U-net channels, in channels, sampling steps). Specific values are provided for each hyperparameter for the Stocks, Energy, MuJoCo, and Sine datasets.

This table presents the hyperparameters used for long-term unconditional generation experiments. It details the settings for three datasets: FRED-MD, Temperature Rain, and NN5 Daily. The hyperparameters are categorized into general settings (image size, learning rate, batch size), delay embedding parameters (embedding(n), delay(m)), short-time Fourier transform parameters (n_fft, hop_length), and diffusion model parameters (U-net channels, in channels, sampling steps). The table provides a comprehensive overview of the configuration used for each dataset in the long-term unconditional generation experiments.
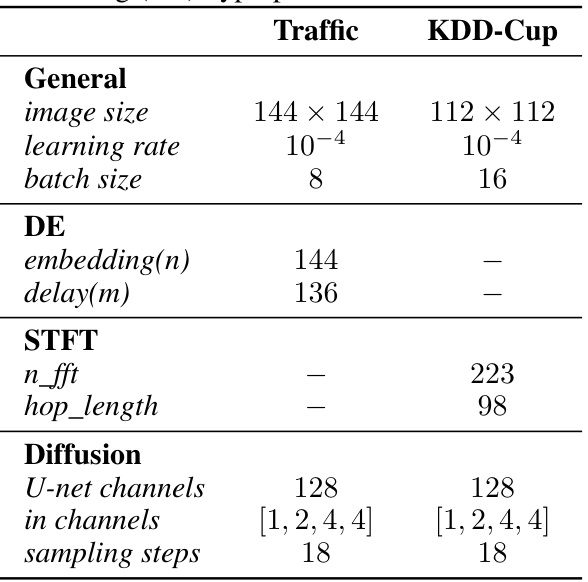
This table lists the hyperparameters used for ultra-long term unconditional generation experiments using the proposed framework. It shows the settings for two datasets, Traffic and KDD-Cup. The hyperparameters are categorized into General settings (image size, learning rate, batch size), Delay Embedding (DE) parameters (embedding size, delay), Short Time Fourier Transform (STFT) parameters (n_fft, hop_length), and Diffusion model parameters (U-net channels, input channels, sampling steps). The table specifies the specific values used for each dataset and parameter type.

This table presents the quantitative results of the proposed method and several baseline methods on short time series unconditional generation tasks. The metrics used for evaluation are discriminative and predictive scores. The discriminative score evaluates the similarity of generated data to real data using a proxy discriminator, while the predictive score assesses the utility of the generated data by training an independent prediction model. The table includes results for multiple datasets, namely Stocks, Energy, and MuJoCo, allowing for a comparison of performance across different data characteristics.
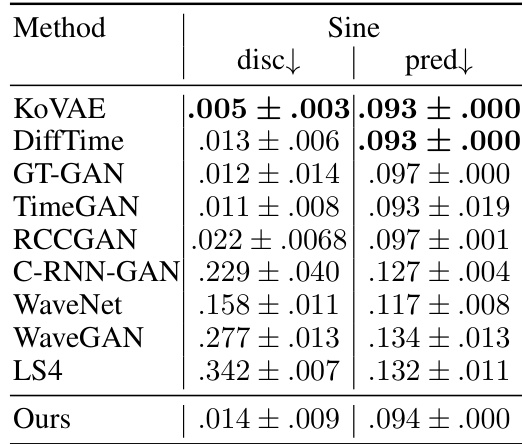
This table presents the performance comparison of different generative models on short time series data for unconditional generation tasks. It shows the discriminative and predictive scores for various models across multiple datasets: Stocks, Energy, and MuJoCo. Lower scores are better for both metrics, indicating better model performance in distinguishing between real and generated data (discriminative score) and making accurate predictions (predictive score). The table helps to understand the relative strengths and weaknesses of various generative models and highlights the performance improvement achieved by the proposed method.

This table presents the Wasserstein distances, a measure of similarity between probability distributions, calculated for the t-SNE embeddings (2D representations) of real and generated time series data. The comparison includes the authors’ method and two other methods (GT-GAN and LS4) across several datasets: Stocks, Energy, MuJoCo, Temp Rain, NN5 Daily, Traffic, and KDD-Cup. Lower Wasserstein distances indicate higher similarity between the real and generated data distributions, suggesting better performance of the generative models.

This table presents the quantitative results comparing the proposed method with state-of-the-art long-term time series generation methods across three real-world datasets: FRED-MD, NN5 Daily, and Temperature Rain. The metrics used are Marginal, Classification, and Prediction, providing a comprehensive evaluation of the unconditional generation performance. Lower values for Marginal and Prediction indicate better performance, while higher values for Classification show improved realism of the generated data.

This table presents the results of the ultra-long unconditional generation task. It compares the performance of three different methods (Latent ODE, LS4, and the proposed method) on two datasets (Traffic and KDD-Cup). The metrics used to evaluate performance include prediction error (pred↓), classification accuracy (class↑), and marginal probability density difference (marg↓). Lower values for pred↓ and marg↓ indicate better performance, while higher values for class↑ indicate better performance. The results demonstrate that the proposed method achieves the best results across both datasets and all metrics.

This table presents the results of the short-term unconditional generation experiments. It compares the performance of the proposed method against several state-of-the-art baselines across three datasets (Stocks, Energy, MuJoCo) and two metrics (discriminative and predictive scores). The discriminative score measures the similarity between generated and real data distributions, while the predictive score assesses the ability of the generated data to predict future values. Lower scores indicate better performance in both metrics.
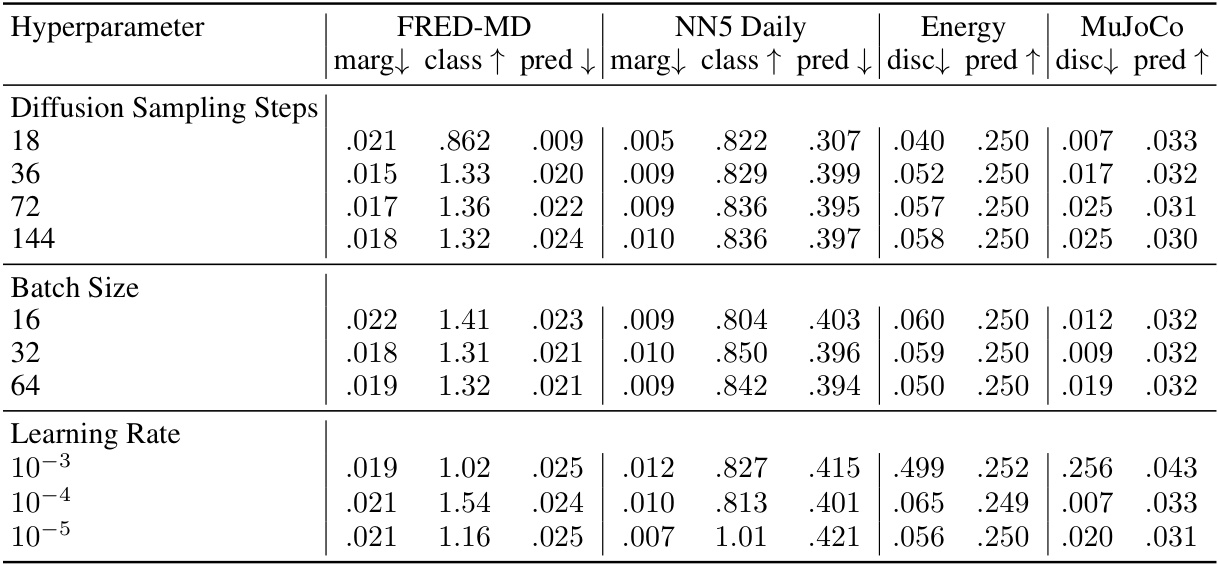
This table presents the results of evaluating different generative models on three short-term time series datasets (Stocks, Energy, and MuJoCo). Each dataset consists of short sequences (length 24). The models are evaluated using two metrics: the discriminative score (disc), which measures how well the generated data resembles the real data, and the predictive score (pred), which evaluates how well the generated data can be used to predict future values. Lower scores are better for both metrics. The table allows comparison of the proposed method’s performance against various existing state-of-the-art generative models for short time series.

This table presents the performance of various generative models on short time series data, specifically focusing on unconditional generation. The models are evaluated using two metrics: discriminative score and predictive score. The discriminative score measures how well the generated data resembles real data, while the predictive score assesses the generated data’s ability to be used for prediction. Lower scores indicate better performance for both metrics. The table includes results across multiple datasets (Stocks, Energy, MuJoCo) to demonstrate the models’ performance across different data characteristics.

This table presents the performance comparison of different generative models on three short time series datasets (Stocks, Energy, MuJoCo) for unconditional generation. Two metrics are used for evaluation: discriminative score and predictive score. The discriminative score measures how well the generated data resembles the real data. The predictive score measures the quality of the generated data used for prediction tasks. Lower scores indicate better performance in both metrics.

This table presents the performance of various generative models on short time series data. The models are evaluated using two metrics: discriminative and predictive. The discriminative score measures the model’s ability to generate realistic data indistinguishable from real data using a discriminator, while the predictive score reflects the ability of the generated time series to be accurately predicted by a separate prediction model. Lower scores are better for both metrics, indicating more realistic and predictable generated time series.

This table presents the results of evaluating several generative models on three short time-series datasets (Stocks, Energy, MuJoCo). Each dataset’s results are broken down into discriminative and predictive scores for each method. Lower scores indicate better performance. The discriminative score measures how well the generated data resembles the real data, and the predictive score assesses the utility of the generated data in a prediction task. The table compares the performance of the proposed method against several strong baselines, showcasing its superior performance across all datasets and metrics.
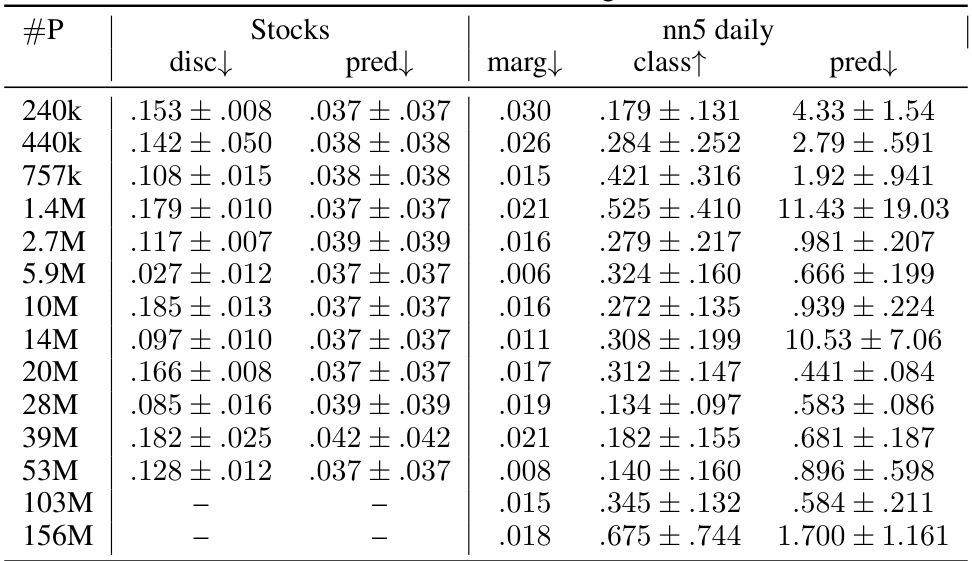
This table presents the performance of various methods on short-term time series generation tasks using three datasets: Stocks, Energy, and MuJoCo. The metrics used are ‘disc’ (discriminative score) and ‘pred’ (predictive score), both lower is better. The table allows comparison of the proposed method to a range of existing generative models for time series data, showcasing its performance relative to state-of-the-art techniques on various metrics and datasets.

This table presents the results of the DiffTime model’s performance on the KDD Cup dataset at different model sizes, showing the marginal, classification, and prediction scores. It demonstrates how the model’s performance changes as its size increases. The table highlights that simply increasing model size doesn’t necessarily improve the results, unlike the method proposed in the paper.

This table presents the results of several generative models on short time series datasets, focusing on unconditional generation tasks. The metrics used are: disc (discriminative score) which measures the model’s ability to generate realistic-looking data indistinguishable from real data, and pred (predictive score) which measures the usefulness of generated data in prediction tasks. Lower disc and pred values indicate better performance. The table shows results for three distinct datasets: Stocks, Energy, and MuJoCo. Each dataset has its own characteristics, such as dimensionality and the presence of noise or periodicity.
Full paper#