↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many machine learning models are trained on large datasets with labels often obtained through crowdsourcing. This introduces a significant challenge: noisy labels. Existing methods attempt to estimate the true label posterior but may overlook potential misspecifications, leading to decreased model accuracy. This is especially problematic in high-noise scenarios.
This paper tackles this issue by proposing a novel approach: conditional distributionally robust optimization (CDRO). CDRO minimizes the worst-case risk by considering a range of possible distributions. The paper develops an efficient algorithm for CDRO, including a novel robust pseudo-labeling technique and a method for adaptive Lagrange multiplier selection. Extensive experiments demonstrate that the proposed method significantly outperforms existing approaches on both synthetic and real-world datasets.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with noisy labeled datasets, a pervasive issue in machine learning. It offers a robust and efficient solution by leveraging conditional distributionally robust optimization, addressing the limitations of existing methods. This opens new avenues for research in handling data uncertainty and improving model accuracy in various applications.
Visual Insights#

This figure shows the average test accuracy achieved by the proposed AdaptCDRP method on CIFAR-10 and CIFAR-100 datasets with different values of the hyperparameter epsilon (ε). The results are shown for three different noise levels (IDN-LOW, IDN-MID, IDN-HIGH) in the synthetically generated noisy labels. The x-axis represents the values of epsilon, and the y-axis represents the test accuracy. The shaded area around each line indicates the standard deviation of the results obtained over five repeated experiments. This figure demonstrates the impact of the robustness hyperparameter on the model’s performance across different noise levels and datasets.

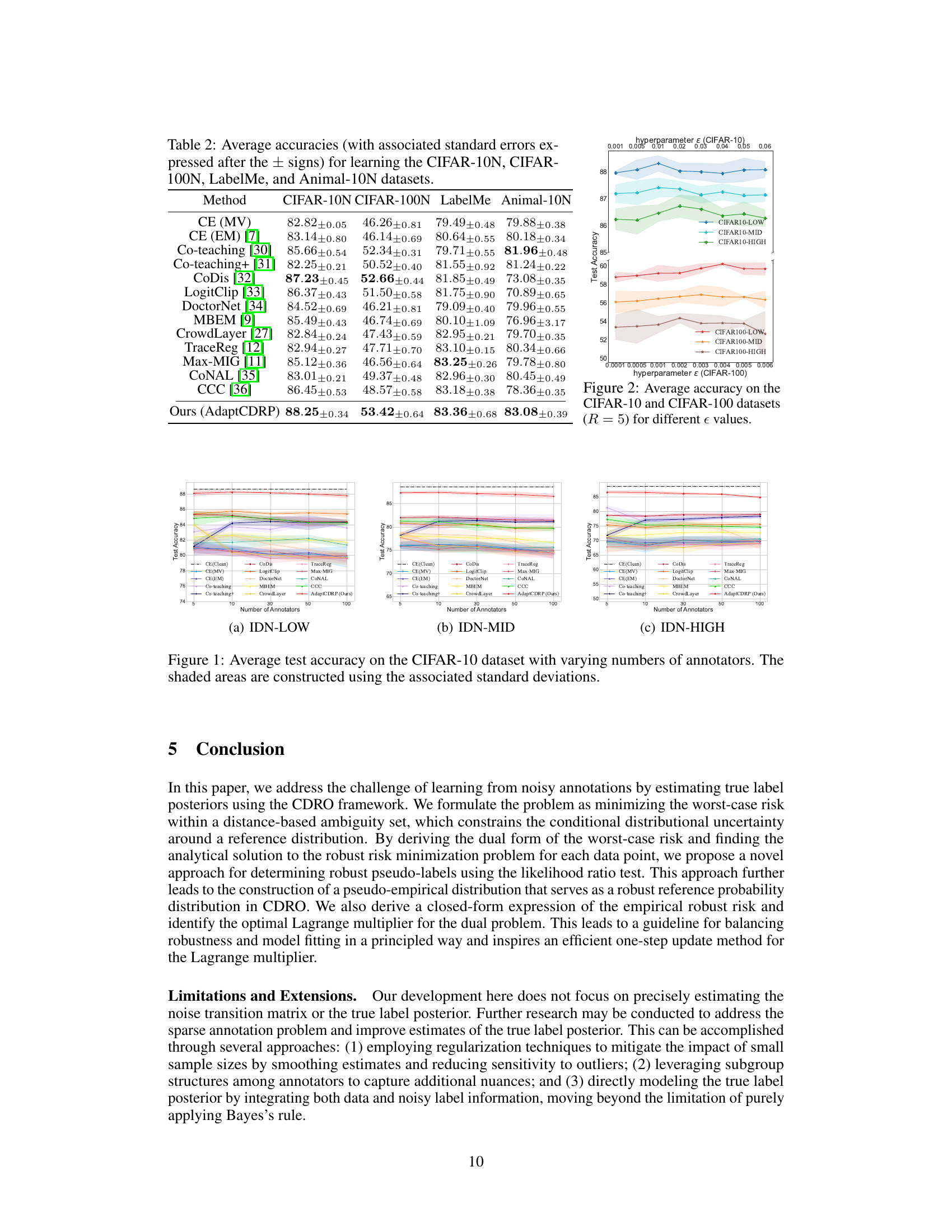
This table presents the average test accuracies achieved by various methods on the CIFAR-10 and CIFAR-100 datasets with different amounts of label noise. The methods compared are several state-of-the-art algorithms for learning with noisy labels, and the proposed AdaptCDRP method. The results show the performance under three different noise levels (low, medium, and high). R=5 indicates that 5 annotators provided labels per image, but only one was randomly selected for training.
In-depth insights#
Noisy Label Learning#
Noisy label learning tackles the challenge of building accurate machine learning models when the training data contains inaccurate or unreliable labels. This is a pervasive problem in many real-world applications where obtaining perfectly labeled data is expensive or impossible. Strategies for addressing noisy labels range from modifying loss functions to make them less sensitive to label errors to employing techniques that identify and either correct or down-weight noisy labels. Robust loss functions, like those based on distributionally robust optimization, focus on minimizing the worst-case risk arising from uncertain label distributions. Ensemble methods leverage the wisdom of the crowd by combining predictions from multiple models trained on different subsets of the data or with different regularization schemes. Meta-learning approaches attempt to learn algorithms that are robust to noise, adapting their training strategies based on the characteristics of the noisy labels. Successfully navigating this challenge leads to more reliable and generalizable models, making noisy label learning a crucial area of research with far-reaching implications.
CDRO Framework#
The CDRO (Conditional Distributionally Robust Optimization) framework offers a robust approach to learning from noisy labels by minimizing the worst-case risk. It addresses the challenge of potential misspecification in estimating true label posteriors, which is a common problem in learning from noisy crowdsourced data. The core idea is to minimize the expected loss under the worst-case conditional distribution within a specified distance of a reference distribution, thereby enhancing model robustness. The framework leverages strong duality in linear programming to derive analytical solutions and efficient algorithms. This allows for a principled balance between robustness and model fitting. A key innovation is the use of a likelihood ratio test and pseudo-labeling to generate a robust reference distribution for the CDRO formulation. The resulting AdaptCDRP algorithm is shown to outperform state-of-the-art methods on various datasets with synthetic and real-world noisy labels, showcasing the efficacy and generality of the CDRO framework in dealing with the complexities of noisy label learning.
Robust Pseudo-labels#
The concept of “Robust Pseudo-labels” in the context of noisy-label learning is crucial. It addresses the challenge of directly using noisy labels for training by creating reliable pseudo-labels. Robustness is achieved by incorporating mechanisms that mitigate the impact of label noise, possibly using techniques like likelihood ratio tests or confidence thresholds to filter out unreliable labels. This filtering process ensures that only high-confidence predictions become pseudo-labels, thereby improving the quality of training data and reducing overfitting to noisy examples. The creation of robust pseudo-labels often involves estimating an accurate label posterior distribution, considering both the instance features and the noisy labels. This refined data then guides a more robust training process, improving model generalization and performance. Key aspects include the balance between robustness (resisting noise effects) and model accuracy, algorithm efficiency in computing the robust pseudo-labels, and the ability to extend the method to more complex scenarios, such as multi-class classification.
Empirical Robustness#
Empirical robustness in machine learning assesses a model’s performance consistency across various datasets and conditions. Robust models generalize well, exhibiting stability even with noisy, incomplete, or differently distributed data than those used for training. This contrasts with models showing high accuracy on training data but poor performance on unseen data, indicating a lack of robustness. Evaluating empirical robustness involves rigorous testing on diverse datasets, simulating real-world scenarios like noisy labels or data corruption. Techniques to improve robustness include regularization, data augmentation, ensemble methods, and adversarial training. Analyzing the effects of hyperparameters on robustness is vital, finding the optimal settings that balance performance with stability. Quantifying robustness requires careful selection of metrics that accurately capture a model’s resilience to variations, possibly using statistical measures beyond simple accuracy to understand the degree of robustness. Ultimately, a robust model provides reliable predictions in real-world applications, rather than merely maximizing accuracy on specific training data.
Future Research#
Future research directions stemming from this work could explore several promising avenues. Extending the CDRO framework to handle more complex noise models beyond the current instance-dependent approach is crucial for real-world applicability. This could involve incorporating annotator-specific biases or temporal dependencies in label quality. Developing more efficient algorithms for CDRO remains important, particularly for large-scale datasets. Investigating alternative optimization techniques or approximations to reduce computational complexity would be beneficial. The use of the Wasserstein distance in defining the ambiguity set could be further investigated by considering other divergence measures, exploring their impact on model robustness and computational efficiency. Empirical analysis across a broader range of datasets and tasks, including those with high-dimensional features or complex relationships, is vital to assess the generalizability of CDRO approaches. Finally, the robust pseudo-labeling algorithm warrants further investigation into alternative methods for likelihood ratio construction and a more nuanced approach to handling uncertain data points, to further enhance its robustness and accuracy. This would lead to a more robust and effective approach to learning from noisy labels.
More visual insights#
More on figures

This figure shows the average test accuracy and standard deviation across different numbers of annotators (5, 10, 30, 50, 100) for the CIFAR-10 dataset. The results are broken down by three annotator groups representing different levels of expertise: IDN-LOW (low noise), IDN-MID (medium noise), and IDN-HIGH (high noise). Each data point represents the average performance across multiple trials. The shaded areas illustrate the standard deviation, providing a measure of variability for each data point. The figure demonstrates how the proposed method (AdaptCDRP) performs compared to other methods under varying levels of annotation sparsity.

This figure shows the average test accuracy achieved by different methods on the CIFAR-10 dataset under various noise conditions and varying number of annotators (5,10,30,50,100). The shaded area around each line represents the standard deviation. The results demonstrate the performance of AdaptCDRP across different levels of annotation sparsity and noise.

This figure shows the average accuracy of the robust pseudo-labels generated by the proposed AdaptCDRP method during the training process on CIFAR-10 and CIFAR-100 datasets. The number of annotators (R) is fixed at 5. Three different groups of annotators with varying levels of expertise (IDN-LOW, IDN-MID, and IDN-HIGH) are presented, illustrating the impact of noise level on the pseudo-label accuracy. The plot shows how the accuracy evolves over iterations, providing insights into the performance of the robust pseudo-labeling algorithm under different noise conditions and datasets.
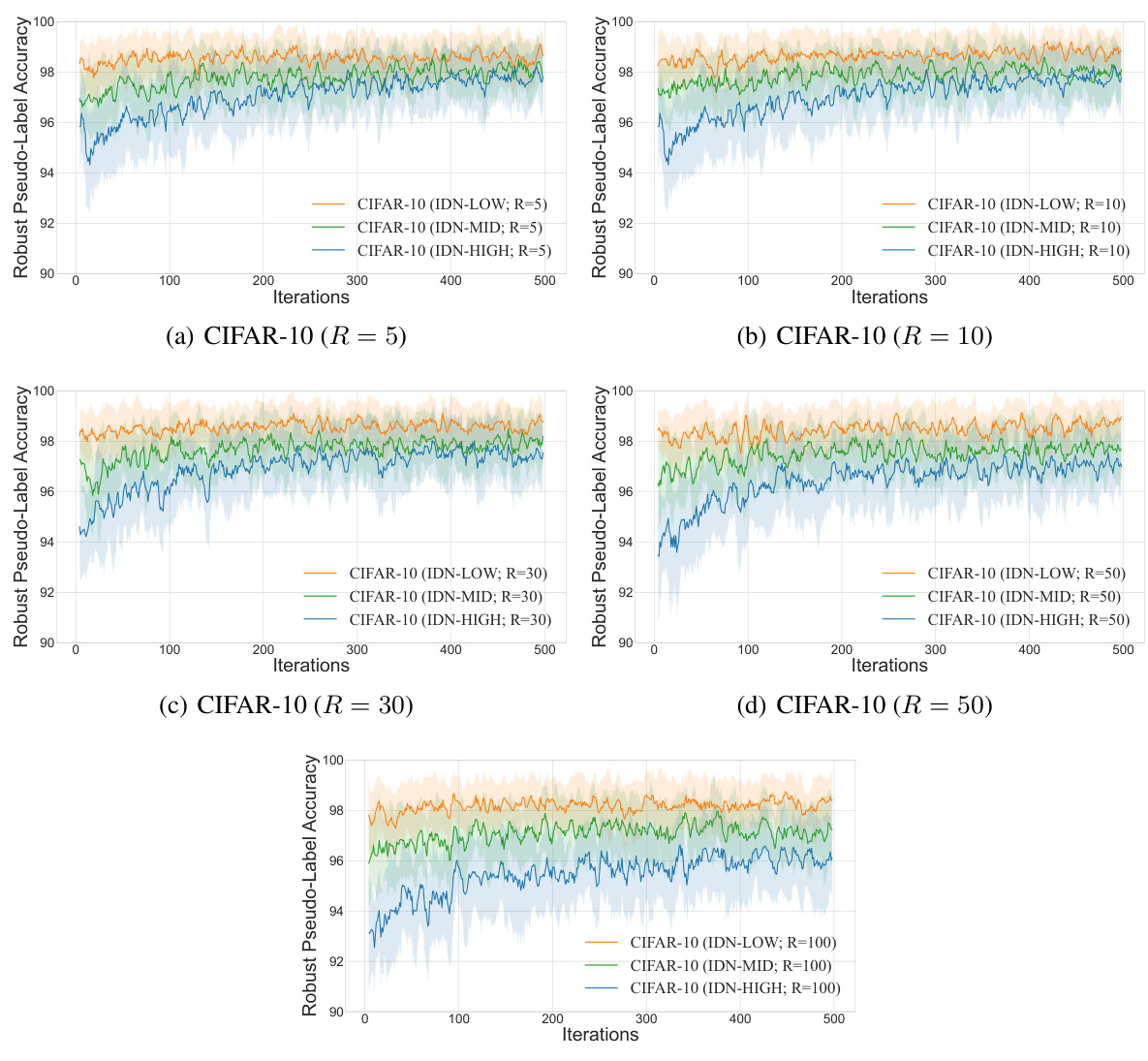
This figure shows the average accuracy of robust pseudo-labels on the CIFAR-10 dataset for different numbers of annotators (R=5, 10, 30, 50, 100) and for different noise levels (IDN-LOW, IDN-MID, IDN-HIGH). The shaded areas represent the standard deviations of the accuracies across multiple runs. The figure illustrates how the accuracy of the robust pseudo-labels changes during the training process. The accuracy is generally high and stable across different numbers of annotators and noise levels.
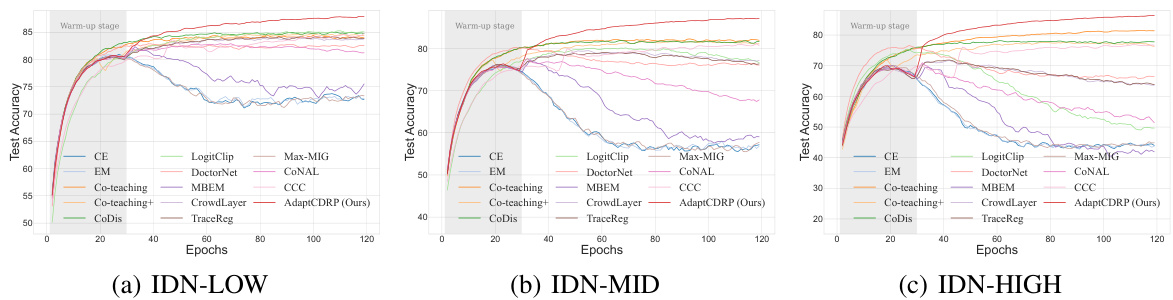
This figure shows the test accuracy on the CIFAR-10 dataset with R=5 annotators over the training epochs for different noise levels (IDN-LOW, IDN-MID, IDN-HIGH). It compares the performance of AdaptCDRP to several baseline methods. The shaded region at the beginning indicates the warm-up period where the model is trained on the noisy labels before applying the robust pseudo-labeling strategy.
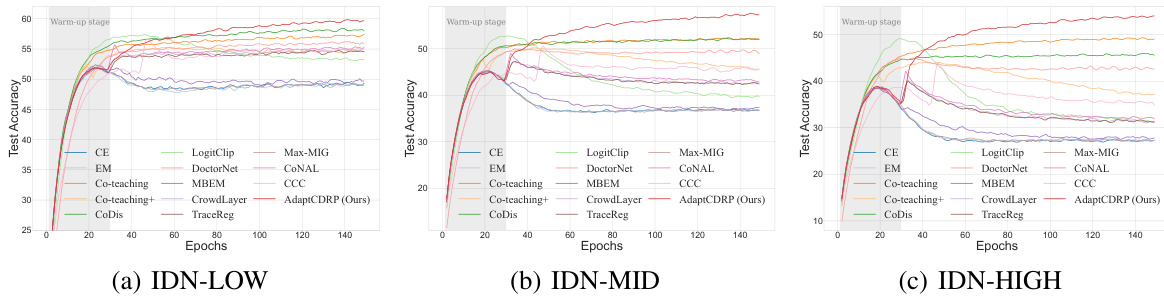
This figure shows the average test accuracy of different methods on the CIFAR-10 dataset with varying numbers of annotators. The x-axis represents the number of annotators, and the y-axis represents the test accuracy. Different lines represent different methods, including the proposed AdaptCDRP method and several baseline methods. The shaded area around each line represents the standard deviation of the test accuracy. The figure is divided into three subfigures (a), (b), and (c), corresponding to different levels of noise in the labels (IDN-LOW, IDN-MID, IDN-HIGH). The figure demonstrates the performance of the proposed method under various levels of noise and with varying degrees of labeling completeness (different numbers of annotators).
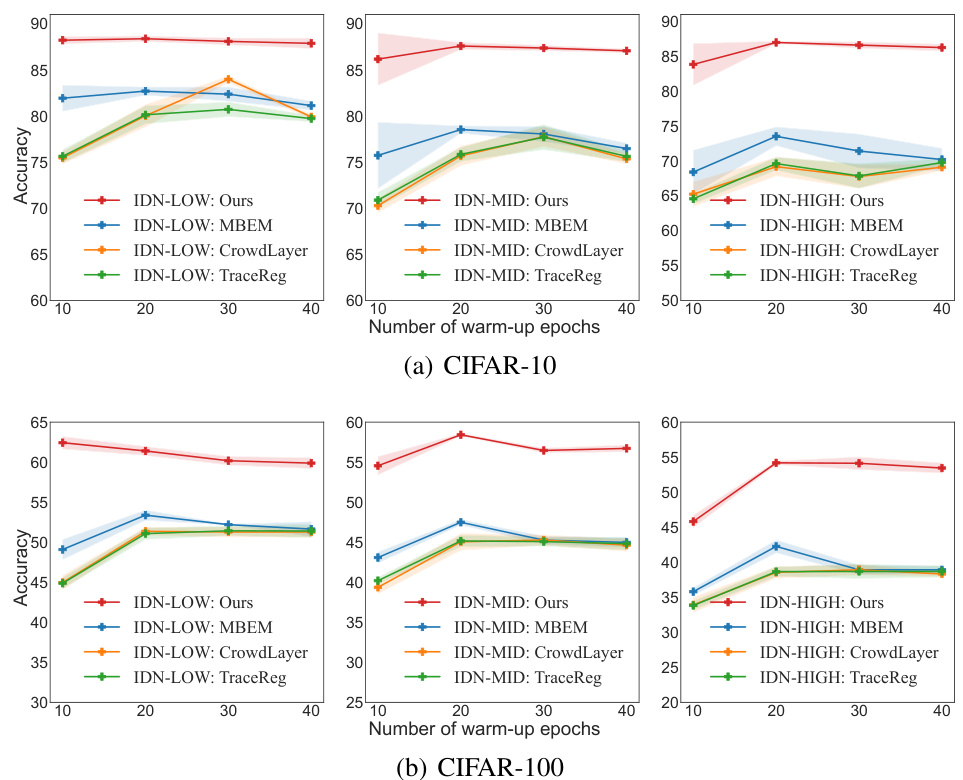
The figure shows the impact of different warm-up durations on the performance of the proposed AdaptCDRP method and several baseline methods. The results are shown for the CIFAR-10 and CIFAR-100 datasets, with different noise levels (IDN-LOW, IDN-MID, IDN-HIGH). The x-axis represents the number of warm-up epochs, and the y-axis represents the test accuracy. Error bars are included to show the standard deviation across multiple runs.

This figure shows the average accuracy of robust pseudo-labels generated by the AdaptCDRP method on the CIFAR-10 dataset with 200 annotators. Three different methods for estimating the noise transition matrix were used: frequency counting, GeoCrowdNet (F), and GeoCrowdNet (W). The results show that the GeoCrowdNet methods provide slightly higher average accuracy of pseudo-labels compared to the frequency counting approach, particularly in the IDN-LOW condition. The error bars indicate the standard deviation across five random trials. The x-axis represents training iterations and the y-axis represents robust pseudo-label accuracy.
More on tables

This table presents the average test accuracies achieved by different methods on four real-world datasets with human-annotated noisy labels. The methods are compared across the four datasets. Standard errors are included to indicate the variability in the results.

This table presents the average accuracies achieved by different methods on the CIFAR-10 and CIFAR-100 datasets. The results are shown for three different noise levels (IDN-LOW, IDN-MID, IDN-HIGH) and the number of annotators is fixed at 5 (R=5). The methods used are various state-of-the-art techniques for learning from noisy labels, including the proposed AdaptCDRP method. The table highlights the superiority of the AdaptCDRP method across all noise levels and datasets, demonstrating its robustness to noisy annotations.

This table presents the average accuracies achieved by various methods on the CIFAR-10 and CIFAR-100 datasets with different levels of label noise (IDN-LOW, IDN-MID, and IDN-HIGH). The results are presented for comparison, showing the performance of the proposed AdaptCDRP method against existing state-of-the-art techniques. Each accuracy value is accompanied by its standard error.

This table presents the average test accuracies achieved by AdaptCDRP and several other state-of-the-art methods on four real-world datasets containing human-annotated noisy labels. Each accuracy is reported with its associated standard error. The datasets used include CIFAR-10N, CIFAR-100N, LabelMe, and Animal-10N, each with varying characteristics in terms of noise levels and data properties. This allows for a comprehensive evaluation of the model’s performance in diverse real-world scenarios.
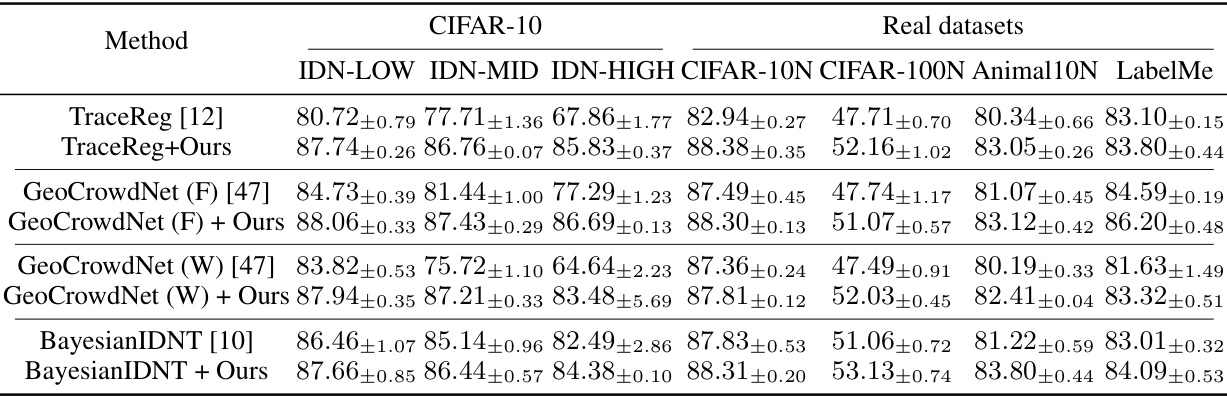
This table presents the average test accuracies achieved by the proposed AdaptCDRP method and various other state-of-the-art (SOTA) methods on the CIFAR-10 and CIFAR-100 datasets. The results are shown for different levels of label noise (IDN-LOW, IDN-MID, IDN-HIGH), representing low, medium, and high levels of noise, respectively. The number of annotators (R) is fixed at 5. The table allows for a comparison of the AdaptCDRP’s performance against other methods under varying levels of label noise.

This table presents the average test accuracies achieved by the proposed AdaptCDRP method on the CIFAR-10 dataset using 200 annotators. Three different methods for estimating the noise transition matrix are compared: frequency counting, and the GeoCrowdNet (F) and GeoCrowdNet (W) penalty methods from [47]. The results are shown for three different noise levels (IDN-LOW, IDN-MID, and IDN-HIGH). The table highlights the impact of using more advanced noise transition matrix estimation methods on the performance of the proposed method.
Full paper#