Globally Q-linear Gauss-Newton Method for Overparameterized Non-convex Matrix Sensing

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in optimization and machine learning because it presents a novel method that significantly improves the convergence rate for solving a challenging non-convex problem. The global Q-linear convergence achieved by the proposed AGN method is a substantial advancement over existing methods and opens up new avenues for tackling similar overparameterized non-convex optimization problems, such as those commonly found in deep learning. The method’s computational efficiency and its robustness to saddle points also add to its practical significance, making it a valuable tool for a wide range of applications.

Visual Insights

#

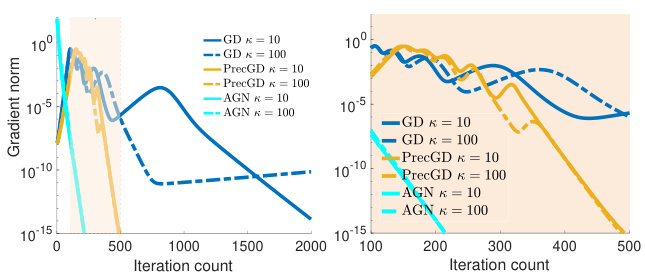
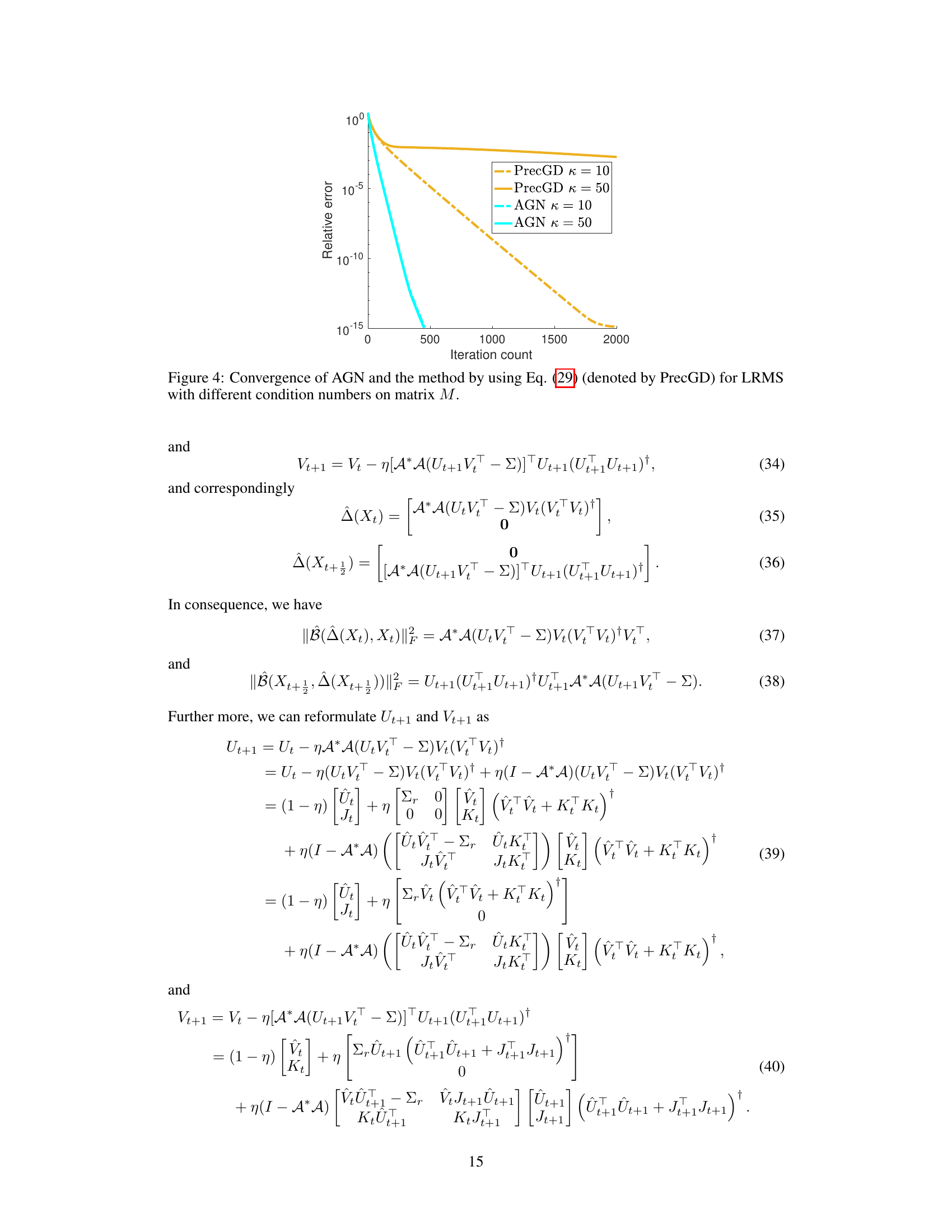
This figure compares the gradient norm of three different algorithms: Gradient Descent (GD), Preconditioned Gradient Descent (PrecGD), and the Approximated Gauss-Newton (AGN) method proposed in the paper. The left subplot shows the overall gradient norm evolution across many iterations, while the right subplot zooms into the iterations 100 to 500 to better visualize the behavior of AGN in the later stage. The plot demonstrates that AGN achieves significantly faster convergence than the other methods, with its gradient norm decreasing linearly to zero, while PrecGD experiences oscillations before converging, and GD shows a much slower convergence rate.

This table compares the iteration complexity of four different algorithms (GD, PrecGD, ScaledGD(λ), and AGN) used for solving the non-convex low-rank matrix sensing problem. The comparison considers the initialization method (random or spectral) and shows the iteration complexity required to achieve a desired level of accuracy (ε). The results highlight the different convergence rates and the influence of the condition number (κ) and initialization on the efficiency of each algorithm.

In-depth insights

#

AGN: Q-Linear Convergence

#

The heading “AGN: Q-Linear Convergence” suggests a focus on proving the global Q-linear convergence of an Approximated Gauss-Newton (AGN) method. This is a significant contribution because Q-linear convergence guarantees a geometric rate of convergence to a global optimum, implying significantly faster convergence than existing methods like gradient descent, especially in high-dimensional, non-convex settings which are often plagued by saddle points and slow convergence. The analysis likely involves demonstrating that the AGN iterates consistently reduce the objective function, ultimately leading to the global optimum, while also maintaining a specific rate of decrease, independent of problem conditioning. The proof might leverage techniques from optimization theory, potentially including properties of the Hessian, and may incorporate assumptions like the restricted isometry property (RIP) to manage the non-convexity of the underlying problem and ensure favorable behavior. Overparameterization, where the model has more parameters than strictly necessary, could also play a key role, possibly simplifying the optimization landscape and facilitating global convergence. Overall, this section aims to provide a rigorous mathematical justification for AGN’s efficiency and reliability in solving challenging low-rank matrix sensing problems.

Overparameterization Effects

#

Overparameterization, where the number of parameters exceeds the number of data points, presents a fascinating paradox in machine learning. It often leads to improved generalization despite the risk of overfitting. In the context of low-rank matrix sensing, overparameterization can eliminate spurious local minima, simplifying the optimization landscape and facilitating convergence to the global optimum. Gradient descent, while effective, can be slowed considerably by the presence of saddle points, a problem exacerbated by overparameterization. This highlights the need for more sophisticated optimization algorithms, like the approximated Gauss-Newton method proposed in this paper, that can effectively avoid saddle points and achieve faster convergence. The key benefit of overparameterization lies in creating a more benign optimization landscape, reducing the likelihood of getting stuck in suboptimal solutions. The challenge, however, lies in managing the increased computational cost associated with the larger number of parameters. Understanding the interplay between overparameterization, optimization algorithms, and the convergence rate remains a crucial area of ongoing research.

Saddle Point Analysis

#

Saddle points, critical points where the gradient is zero but are neither local minima nor maxima, significantly impact the convergence of gradient-based optimization algorithms. The analysis focuses on the behavior of gradient descent (GD), preconditioned gradient descent (PrecGD), and the proposed approximated Gauss-Newton (AGN) method near saddle points. A key finding is that AGN exhibits substantially different behavior than GD and PrecGD. GD and PrecGD struggle to escape saddle points, experiencing slowdowns in convergence rate, especially for ill-conditioned problems or in the presence of overparameterization. In contrast, AGN demonstrates a notable ability to quickly navigate away from saddle points, achieving a significant and consistent reduction in the objective function value near such points, regardless of the problem’s conditioning. This robust performance is attributed to the unique properties of AGN, specifically its ability to avoid being trapped by the saddle points and achieve a Q-linear convergence rate.

Algorithm Comparisons

#

A comparative analysis of algorithms is crucial for evaluating their efficiency and effectiveness. A thoughtful approach would involve comparing algorithms across multiple metrics, including computational complexity, convergence rate, memory usage, and robustness to noise or outliers. Furthermore, the analysis should consider the specific characteristics of the problem being solved and different parameter settings. For example, some algorithms might perform well in low-rank matrix sensing with overparameterization while others struggle. The analysis should also account for various initialization methods. The final comparison should synthesize the findings to offer insights into which algorithms are preferable under various circumstances and their strengths and weaknesses. Ideally, the comparison would use benchmark datasets and provide visual representation, like graphs, for easier interpretation. Detailed analysis of each algorithm’s runtime performance (including setup and iteration cost) and scalability characteristics is vital.

Future Research

#

Future research directions stemming from this work could explore extending the approximated Gauss-Newton method to other non-convex optimization problems beyond matrix sensing, such as those encountered in deep learning. Investigating the impact of different initialization strategies on the convergence rate and global optimality is crucial. A deeper theoretical analysis of the algorithm’s convergence properties under weaker assumptions, potentially relaxing the RIP condition, would further strengthen its applicability. Finally, developing efficient implementations and scaling the algorithm to handle massive datasets common in real-world applications is a practical next step. This could involve exploring distributed or parallel computing techniques to accelerate the optimization process.

More visual insights

#

More on figures

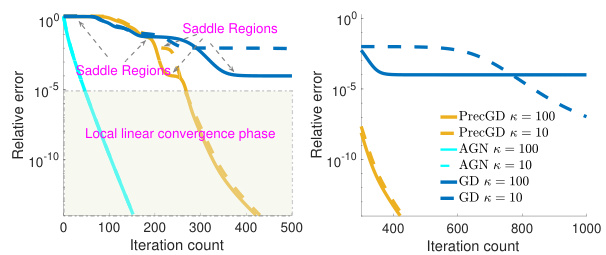
This figure compares the convergence of three different algorithms (PrecGD, GD, and AGN) for solving the overparameterized non-convex low-rank matrix sensing problem. The x-axis represents the number of iterations, and the y-axis represents the relative error. The left panel shows the initial phase of convergence for all three algorithms with condition number (κ) values of 10 and 100. The right panel zooms in on the convergence behavior after 300 iterations, highlighting how AGN significantly outperforms GD and PrecGD in terms of speed and robustness to saddle points. The plots demonstrate that AGN achieves a faster convergence rate compared to both GD and PrecGD, especially in escaping saddle regions where GD and PrecGD struggle.

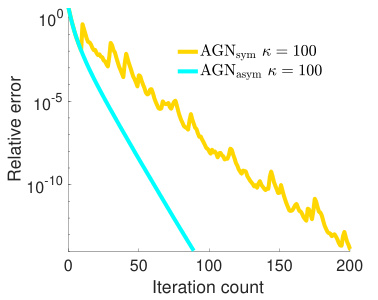
This figure compares the convergence of the AGN method under two different parameterizations for symmetric low-rank matrix sensing: symmetric and asymmetric. The y-axis represents the relative error, while the x-axis shows the iteration count. The plot shows that the asymmetric parameterization leads to significantly faster convergence than the symmetric parameterization. This highlights the importance of parameterization choice when using the AGN method for symmetric low-rank matrix sensing problems.

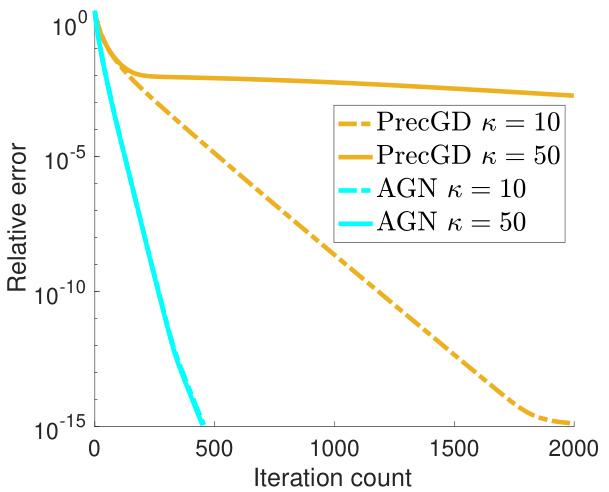
This figure compares the convergence speed of three different algorithms: PrecGD, GD, and AGN, for solving the overparameterized non-convex low-rank matrix sensing problem. The x-axis represents the number of iterations, and the y-axis represents the relative error. The different lines represent the performance of each algorithm under different condition numbers (κ = 10 and κ = 100). The figure shows that AGN converges much faster than PrecGD and GD, especially in the presence of saddle points, and that its convergence is less affected by the condition number.

Full paper

#