↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Instrumental variable regression (IVR) is crucial for causal inference, but traditional methods are computationally expensive and struggle with streaming data. Existing approaches often rely on two-stage estimation or reformulate the problem as minimax optimization, both of which are inefficient and introduce approximation errors. This introduces bias and slows down the convergence of algorithms.
This paper tackles these limitations by directly solving IVR as a conditional stochastic optimization problem, proposing novel streaming algorithms. These algorithms leverage unbiased stochastic gradient estimators, eliminating the need for matrix inversions or mini-batches, resulting in efficient online IVR with improved convergence rates. The paper showcases the benefit of its approach over recent methods by avoiding the need to explicitly model and estimate the relationship between independent and instrumental variables. Numerical experiments are performed to confirm this.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working with streaming data and causal inference. It offers efficient online algorithms for instrumental variable regression, overcoming limitations of existing methods. This opens new avenues for real-time causal analysis in various fields, impacting research in econometrics, healthcare, and social sciences.
Visual Insights#
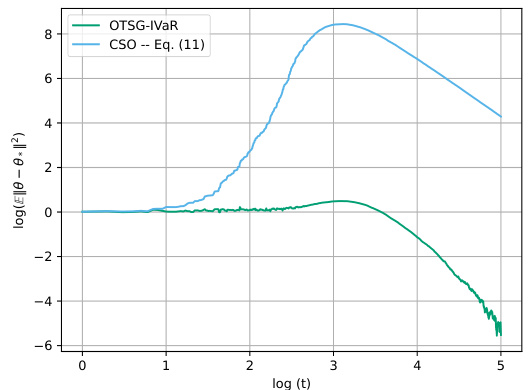
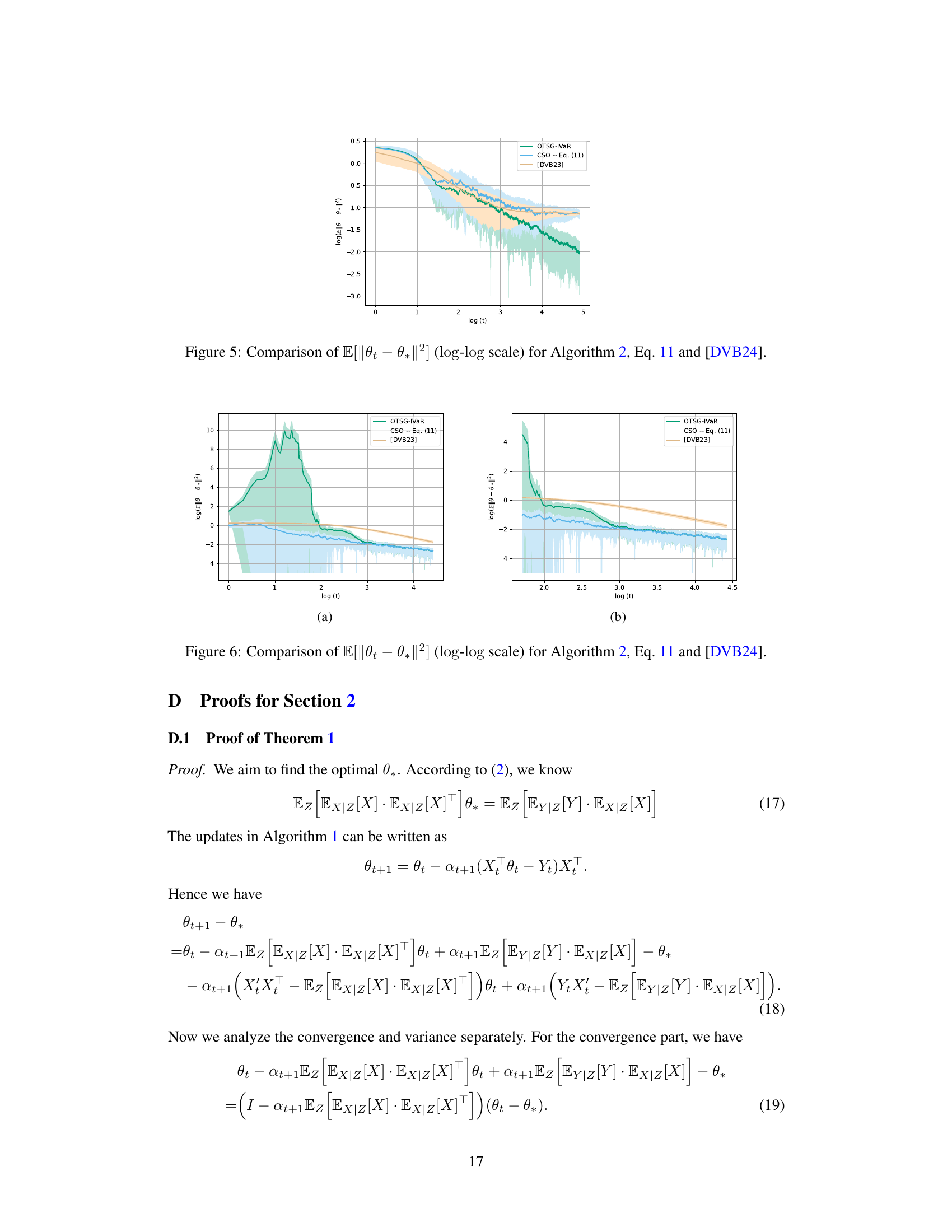
The figure shows the comparison between Algorithm 2 (OTSG-IVaR) and the updates in equation (11) (CSO) in terms of the log of the mean squared error of theta (||θ - θ*||²) against log of the iterations (t). While Algorithm 2 converges smoothly to a low error, the updates in equation (11) initially diverge before slowly converging, indicating inferior performance. The experimental setup details are provided in Appendix C.2.

This table compares the per-iteration memory costs and number of arithmetic operations for four different instrumental variable regression (IVaR) algorithms: the original O2SLS algorithm from Della Vecchia and Basu (2023), the updated O2SLS algorithm (with matrix form updates), the Two-sample One-stage Stochastic Gradient IVaR (TOSG-IVaR), and the One-sample Two-stage Stochastic Gradient IVaR (OTSG-IVaR). The table highlights the computational efficiency of the proposed algorithms (TOSG-IVaR and OTSG-IVaR) compared to the O2SLS algorithms. The memory cost and arithmetic operations are expressed in Big O notation as a function of the dimensions of the variables (dx, dz).
In-depth insights#
IVaR’s Evolution#
Instrumental Variable Regression (IVaR) has seen significant evolution. Early methods relied on two-stage least squares (2SLS), a simple but potentially biased approach. Minimax optimization emerged as a more sophisticated alternative, framing IVaR as a conditional stochastic optimization problem. However, this approach proved computationally expensive and involved approximations. Recent advancements focus on direct solutions to the conditional stochastic optimization problem using streaming algorithms. This enables fully online IVaR with streaming data, avoiding the need for matrix inversions or minibatching. These new algorithms leverage two-sample or one-sample oracles to create unbiased gradient estimators, significantly improving efficiency and addressing the ‘forbidden regression’ problem inherent in 2SLS. The shift from minimax to direct optimization methods represents a major advancement, offering both theoretical improvements and practical benefits for handling high-dimensional or streaming data.
Streaming IVaR#
Streaming IVaR addresses the challenge of performing instrumental variable regression (IVaR) on data that arrives sequentially, a common scenario in real-time applications. Traditional IVaR methods often require processing the entire dataset at once, making them unsuitable for streaming settings. Streaming IVaR algorithms aim to update the IVaR estimates incrementally as new data arrives, without needing to store or reprocess past data. This approach is crucial for efficiency and scalability when dealing with massive or continuously generated datasets. Key challenges in streaming IVaR include handling data dependencies, managing computational costs for online updates, and maintaining statistical consistency. Different techniques, such as stochastic gradient methods and online two-stage least squares, have been proposed to tackle these challenges. A critical aspect is ensuring convergence guarantees and theoretical bounds on estimation error in the streaming setting. Furthermore, the trade-off between computational efficiency and statistical accuracy needs careful consideration. Finally, practical applications of streaming IVaR are wide-ranging, including online A/B testing, real-time causal inference, and adaptive control systems.
Two-Sample Oracle#
The concept of a ‘Two-Sample Oracle’ in the context of instrumental variable regression with streaming data is a crucial innovation. It elegantly addresses the challenge of estimating causal effects when dealing with endogenous variables and unobservable confounders. The oracle’s ability to provide two independent samples of the independent variable (X), conditioned on the instrument (Z), is key. This cleverly sidesteps the need for explicitly modeling the relationship between Z and X, which is often problematic due to the ‘forbidden regression’ issue, thus avoiding potential biases. By constructing an unbiased stochastic gradient estimator using these independent samples, the proposed method significantly improves efficiency and accuracy. This unbiased estimator is particularly powerful in the streaming data setting because it doesn’t require nested sampling or mini-batches, both of which can be computationally expensive. The method’s effectiveness hinges on the availability of this oracle, making its accessibility a significant practical consideration. Overall, the two-sample oracle approach offers a more direct and efficient way to address complex causal inference problems in the streaming data paradigm, showcasing the power of clever algorithmic design to overcome long-standing challenges.
One-Sample Oracle#
The ‘One-Sample Oracle’ scenario presents a more realistic, yet challenging, situation for instrumental variable regression. Unlike the ‘Two-Sample Oracle’, which provides independent samples, the one-sample approach only offers a single observation (Xt, Yt, Zt) per iteration. This limitation necessitates modifications to gradient estimation, shifting from unbiased to biased estimators. The core challenge is the absence of a readily available independent sample for X, forcing methods to work with a single, potentially noisy estimate. Consequently, algorithms designed for the one-sample oracle often employ two-stage procedures. The first stage focuses on estimating the relationship between Z and X (often involving online updating of model parameters), while the second leverages this estimate, along with Y, to update the model parameters for the causal effect of X on Y. This introduces additional complexity in the analysis and necessitates assumptions on model structure, often favoring linear models to ease mathematical tractability. While it may appear less efficient, this two-stage approach remains important because it mirrors the conditions found in many real-world applications of instrumental variable regression where only single observations per sample are readily available. The analysis for one-sample oracles typically demonstrates slower convergence rates than two-sample counterparts, underscoring the price of limited data availability.
Future Works#
The paper’s conclusion mentions several promising avenues for future research. Extending the theoretical analysis to nonlinear models is a significant challenge, requiring a deeper dive into non-convex stochastic optimization and potentially the development of novel analysis techniques. Developing streaming inferential methods for IVaR would greatly enhance the practical applicability of the proposed algorithms. This involves constructing appropriate confidence intervals or hypothesis tests within the streaming setting, which necessitates novel approaches to handle dependent data. Investigating Markovian-type dependency assumptions instead of i.i.d. data would make the algorithms more robust and applicable to a wider range of real-world problems. Finally, exploring alternative loss functions beyond the squared loss and considering more sophisticated gradient estimation techniques, like Multilevel Monte Carlo, will significantly improve the efficiency and efficacy of the algorithms in handling various scenarios. This will lead to the development of more accurate, efficient and broadly applicable algorithms for causal inference in a streaming data environment.
More visual insights#
More on figures

This figure displays the results of Algorithm 1 (Two-sample One-stage Stochastic Gradient IVaR) under various settings. The y-axis shows the expectation of the squared Euclidean norm of the difference between the estimated parameter vector (θ) and the true parameter vector (θ*). This represents the convergence of the algorithm to the true parameters. The x-axis is the iteration number (t). Each subfigure represents a different experimental setup, varying parameters such as the dimension of the independent variable (dx), the dimension of the instrument (dz), the noise level (c), and the model’s non-linearity (Φ(s)). The shaded areas represent standard deviations from multiple runs of the algorithm under each configuration. The experiment results show the effectiveness of the algorithm across these different conditions.

The figure shows the performance of the Two-sample One-stage Stochastic Gradient IVaR (TOSG-IVaR) algorithm under various settings. The y-axis represents the expected squared error between the estimated parameter θ and the true parameter θ*, and the x-axis represents the number of iterations. Different lines represent different combinations of the dimensions of the independent variable (dx), the instrumental variable (dz), the noise variance (c), and the nonlinearity of the relationship between the instrumental variable and the independent variable (ϕ(s)). The shaded area represents the standard deviation of the error across multiple runs. The results demonstrate that the TOSG-IVaR algorithm performs well under diverse conditions.

This figure compares the performance of three different algorithms for instrumental variable regression (IVaR) in terms of the mean squared error (MSE) between the estimated parameters and the true parameters. The algorithms compared are Algorithm 2 (OTSG-IVaR), Equation 11 (a variant of Algorithm 2), and the algorithm proposed by Della Vecchia and Basu in 2024 ([DVB24]). The plot uses a log-log scale to better visualize the convergence behavior over time. The results show that Algorithm 2 converges faster to the true parameters than the other two algorithms, indicating better performance in the online streaming setting.

The figure shows a comparison of the convergence performance between Algorithm 2 (OTSG-IVaR) and the method in equation (11) (CSO). Both methods are used for instrumental variable regression. The results indicate that while the algorithm based on equation (11) initially diverges, Algorithm 2 exhibits more stable and faster convergence. This highlights the benefit of Algorithm 2’s approach in practical applications.
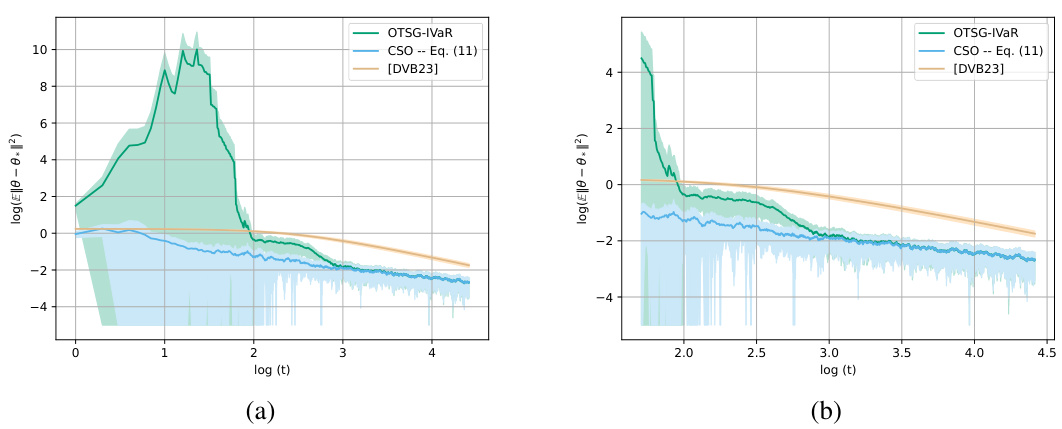
This figure compares the performance of three different algorithms for instrumental variable regression (IVaR) in terms of the expected squared error (E[||θt — θ*||2]) plotted on a log-log scale. The algorithms compared are the proposed One-Sample Two-stage Stochastic Gradient IVaR (OTSG-IVaR) method, a variant using updates from Equation (11) in the paper, and a baseline algorithm from Della Vecchia and Basu (2023). The graphs show how the log of the expected error changes with respect to the log of the number of iterations (t). The purpose is to demonstrate the convergence rate of these methods and to highlight the superior performance of the OTSG-IVaR algorithm.
Full paper#