Towards Understanding Extrapolation: a Causal Lens

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working on out-of-distribution generalization and test-time adaptation because it provides a new theoretical framework and practical algorithms for extrapolation. The framework is important because it addresses the limitations of existing methods that require full target distributions or overlapping support between source and target data, this opens up avenues for developing more robust and reliable machine learning models capable of handling unseen scenarios.

Visual Insights

#

This figure illustrates the concept of extrapolation and the theoretical conditions for its success under different shift types. Panel (a) shows the extrapolation problem: a target sample lies outside the source support region, making classification ambiguous. Panel (b) shows the ‘dense shift’ scenario, where the changing variable affects all image features (e.g., camera angle). Here, extrapolation is possible with moderate shifts, but fails with extreme ones due to ambiguity. Panel (c) shows the ‘sparse shift’ scenario, where changes are confined to a limited subset of features (e.g., background). Extrapolation is robust to severe changes in this case. The figure visually explains Theorems 4.2 and 4.4, linking shift properties to extrapolation success.

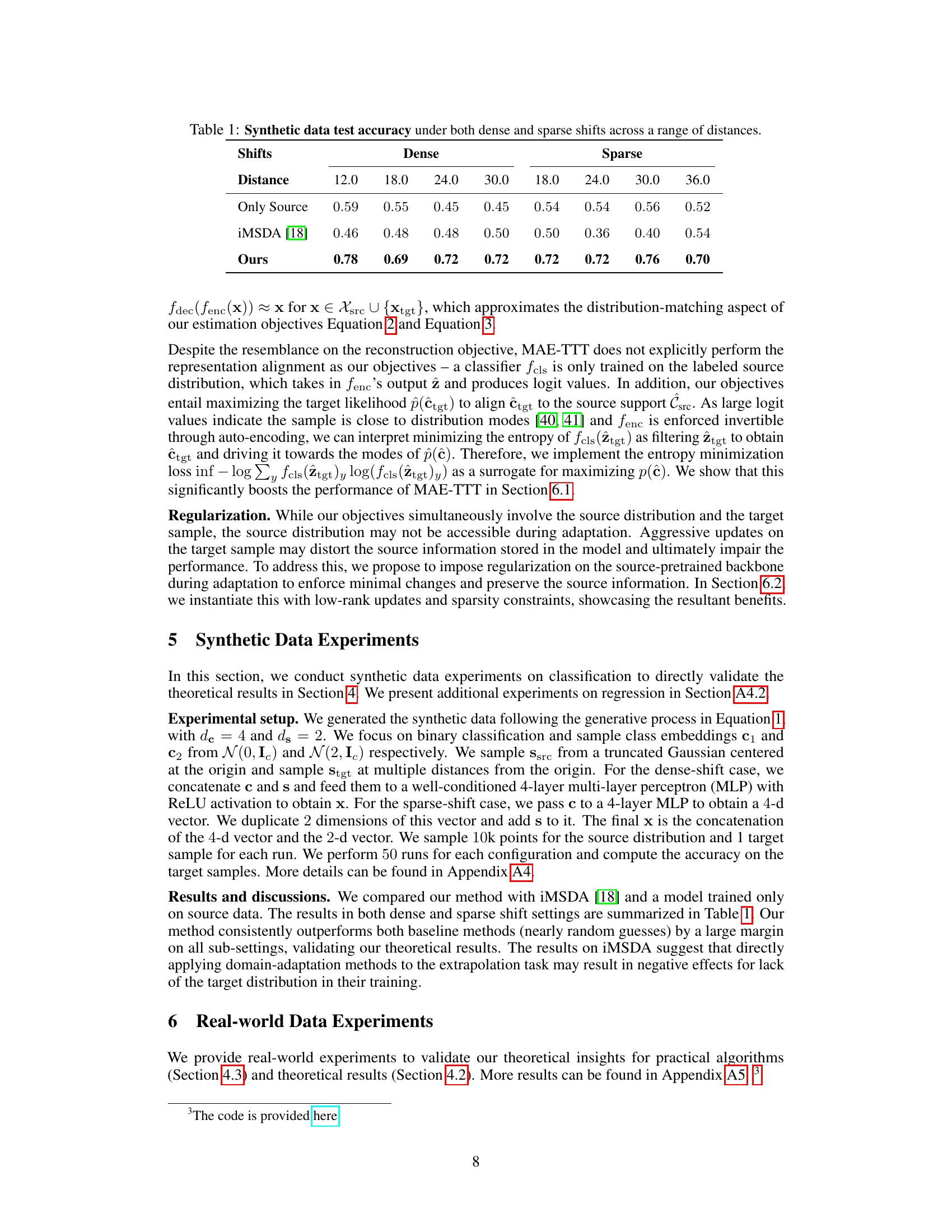
This table presents the results of synthetic data experiments conducted to validate the theoretical findings of the paper. The experiments focus on classification tasks under both dense and sparse shift conditions. The table displays test accuracy for three different methods: 1. Only Source: A baseline representing the model trained only on source data. 2. iMSDA [18]: A state-of-the-art domain adaptation method from prior work. 3. Ours: The proposed method of the current paper. The results are shown for different shift distances, allowing for an evaluation of how each method performs as the distance from the training data increases. The ‘dense’ and ‘sparse’ columns refer to two different types of distribution shifts, affecting different numbers of data dimensions.

In-depth insights

#

Extrapolation Theory

#

Extrapolation theory, in the context of machine learning, seeks to understand how models can generalize beyond the observed training data. A key challenge is defining the conditions under which extrapolation is possible, moving beyond simple interpolation within the training distribution. The paper likely explores various approaches to model extrapolation, potentially leveraging causal inference or latent variable models. Causal models are particularly relevant because they allow for reasoning about the underlying mechanisms generating data, even outside the training set. The framework might introduce assumptions on the nature of distribution shifts (dense vs. sparse shifts) and how these shifts relate to model identifiability. The success of extrapolation hinges on the interplay between the shift’s properties and the underlying data manifold’s smoothness. The theoretical findings likely provide guidance on designing algorithms that perform robust extrapolation, offering valuable insights into the limitations of existing methods and suggesting new directions for research.

Causal Latent Models

#

Causal latent models offer a powerful framework for disentangling complex data by explicitly modeling the causal relationships between latent variables and observed data. By integrating causal reasoning, these models can address limitations of traditional latent variable models, which often struggle with identifying meaningful latent factors and interpreting their effects. A key advantage is the ability to infer counterfactual outcomes, which provides valuable insights into cause-and-effect relationships. This is especially crucial in scenarios where simply observing correlations is insufficient, such as in evaluating policy interventions or understanding the impact of specific factors on a system’s behavior. The design and interpretation of causal latent models require careful consideration of causal assumptions and the identification of relevant causal pathways. However, the advantages in terms of explainability and the potential for more robust and reliable predictions make them an exciting area of active research with broad applications.

Shift Properties’ Role

#

The role of ‘shift properties’ in extrapolation is central to understanding when successful generalization beyond the training distribution is possible. The paper explores how the nature of the shift, whether it’s dense (affecting all data points) or sparse (affecting only a subset), critically influences the identifiability of invariant latent variables. Dense shifts, while potentially more impactful, require stronger conditions on data separability and the proximity of out-of-distribution points to the training support for successful extrapolation. Conversely, sparse shifts offer a more promising avenue, as the invariance of certain features allows extrapolation even with significant out-of-distribution samples. The interplay between manifold smoothness and shift properties is highlighted, with smoothness facilitating identification under dense shifts by maintaining distinct class structures, and sparsity enabling robustness to greater out-of-distribution distances. Ultimately, a deep understanding of these shift properties is key to developing robust extrapolation algorithms, and the paper’s focus on minimal change principles offers a compelling framework for further research in this area.

MAE-TTT Enhancements

#

The MAE-TTT Enhancements section would explore improvements to the Masked Autoencoder-based Test-Time Training (MAE-TTT) method. A key focus would likely be on addressing the limitations of the original MAE-TTT approach. This could involve incorporating additional loss functions, such as an entropy-minimization loss, to better guide the learning process and improve the model’s ability to generalize to unseen data. The addition of a likelihood maximization term to the objective function is a potential enhancement, driving the latent representation of the target sample toward the source distribution’s support. Another potential improvement would be the introduction of regularization techniques, such as sparsity constraints, to prevent overfitting to the target sample and preserve the model’s ability to generalize to other samples. This could also improve the robustness and efficiency of the adaptation process. Ultimately, the enhancements would aim to create a more robust and reliable MAE-TTT method capable of effective extrapolation to out-of-distribution samples, with detailed experimental results demonstrating the effectiveness of the proposed improvements across various datasets and challenging scenarios.

Sparse Shift Advantage

#

The concept of “Sparse Shift Advantage” in the context of extrapolation from a limited number of out-of-distribution samples highlights the crucial role of the nature of the shift. When shifts primarily affect a small subset of features (sparsity), extrapolation becomes significantly more robust even with minimal overlapping support between the source and target distributions. This is because the invariant features retain their informational integrity, allowing for accurate prediction despite the out-of-distribution nature of the new samples. The underlying manifold’s smoothness further moderates the impact of the shift, as smoother manifolds facilitate more accurate generalization. Conversely, dense shifts—where many features are altered—significantly impair extrapolation capabilities, leading to increased uncertainty and ambiguity unless strong assumptions on the separation of the source and target data manifolds are made. This difference underscores the importance of carefully analyzing the nature of distribution shifts in designing robust extrapolation algorithms; leveraging sparsity where possible is key to improving their effectiveness and reliability.

More visual insights

#

More on figures

This figure illustrates the concept of extrapolation and the theoretical conditions proposed in the paper. It shows how changes in the changing variable (s) affect the observed data (x) which lie on manifolds indexed by the invariant variable (c). Panel (a) depicts the challenge of extrapolation: given an out-of-support sample, it’s difficult to determine the correct class manifold. Panel (b) shows that with dense shifts (affecting all image pixels), identifying the invariant variable is possible only with moderate shifts. Panel (c) illustrates that with sparse shifts (affecting only a few pixels), the invariant variable can be identified even with large shifts.

This figure illustrates the causal model used in the paper to represent the data generation process. The latent variable c represents invariant information shared between the source and target distributions. The latent variable s represents the changing factor that distinguishes the source and target data. The variable x is the observed data, and y is the label. The arrows represent causal relationships, indicating that c causally influences both x and y, while s only influences x. The dashed line between c and s suggests a potential statistical dependence, but not necessarily a causal relationship.

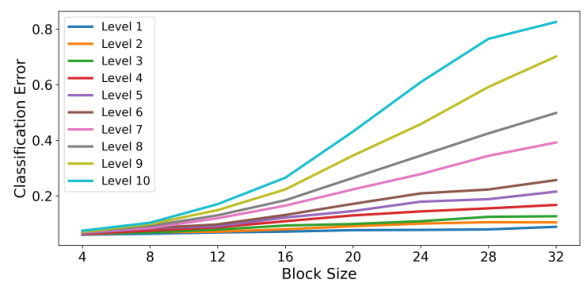
This figure shows the classification error rates obtained by the TENT method under different levels of noise (severity) and different sizes of corrupted regions (scope) in CIFAR-10 images. The x-axis represents the size of the corrupted region (block size), and the y-axis represents the classification error. Each line represents a different noise level, ranging from Level 1 (least severe) to Level 10 (most severe). The results demonstrate that the error rate increases with both increasing noise level and increasing block size. In particular, for larger block sizes (dense shifts), the error rate significantly increases with severity, while for smaller block sizes (sparse shifts), the error rate remains relatively constant across severity levels. This illustrates the trade-off between the shift scope and severity as described in the paper.

More on tables

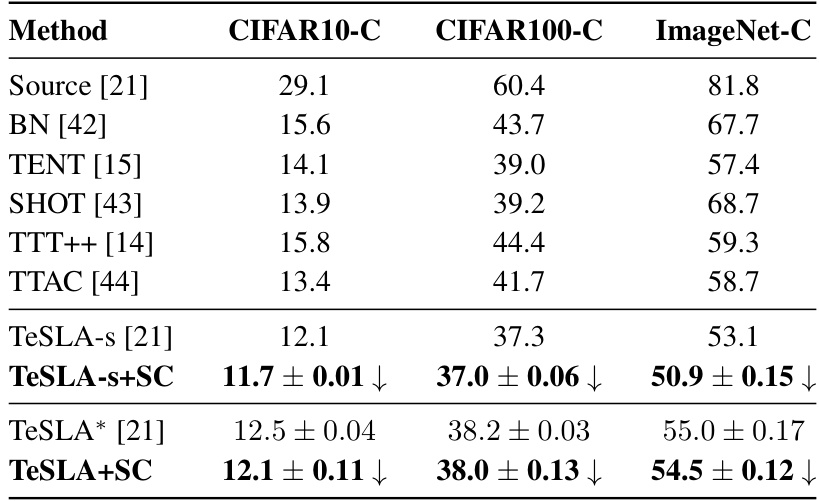
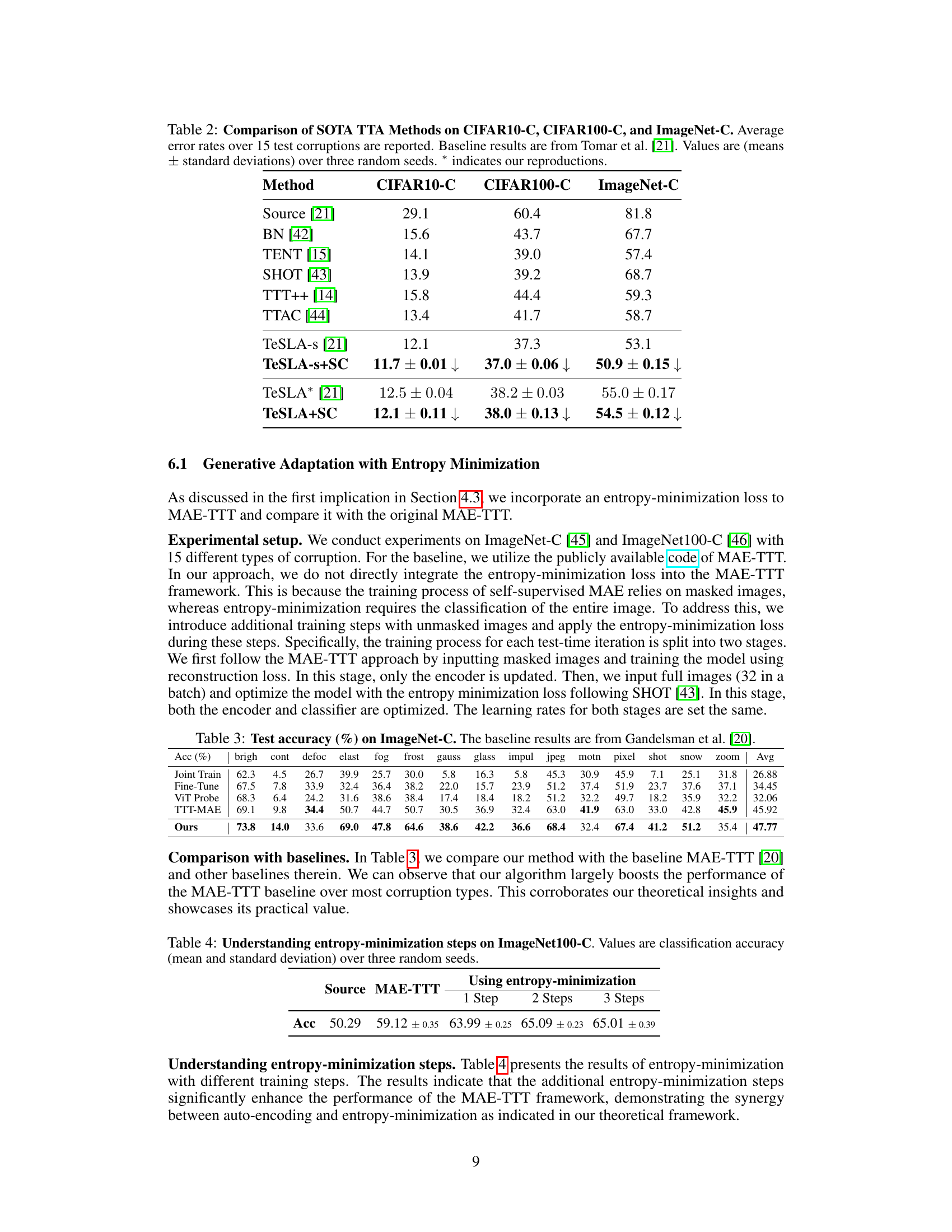
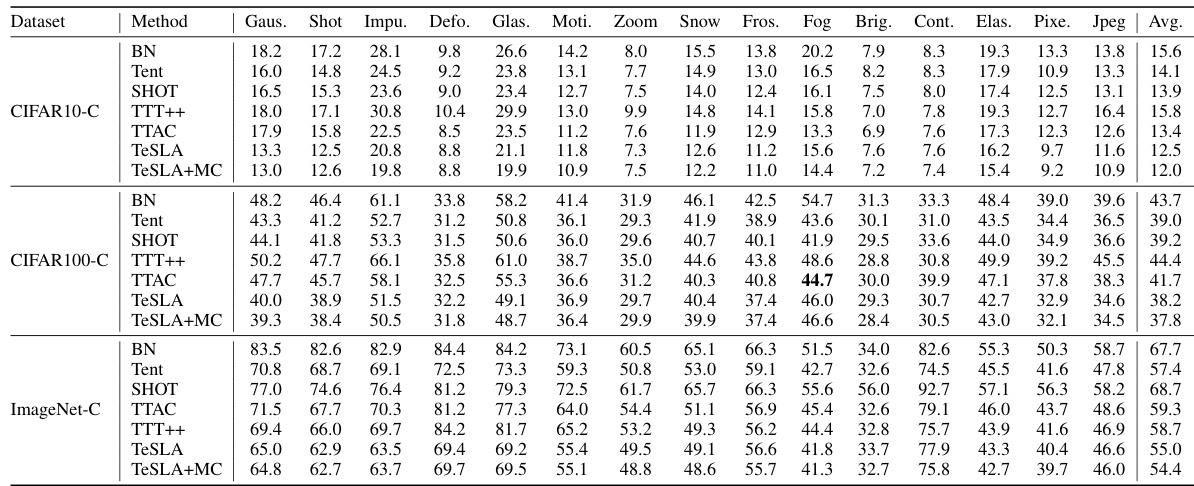
This table compares the performance of several state-of-the-art test-time adaptation (TTA) methods on three corrupted image datasets: CIFAR10-C, CIFAR100-C, and ImageNet-C. The average error rates are presented across 15 different types of corruptions, demonstrating the effectiveness of different techniques in handling distribution shifts during the test phase. The table includes baseline results from a previous study by Tomar et al. [21] for comparison, and error bars (mean ± standard deviation) are provided to indicate variability across three independent runs of each experiment. The authors’ improved method is indicated with a ‘*’.

This table presents the test accuracy results on the ImageNet-C dataset, comparing the proposed method with several baselines (Joint Train, Fine-Tune, ViT Probe, TTT-MAE). The results are broken down by individual corruption types and show the average accuracy across all corruptions. The proposed method demonstrates a significant improvement in accuracy over all baselines.

This table presents the results of adding entropy-minimization steps to the MAE-TTT framework. It shows classification accuracy (mean and standard deviation across three random seeds) on the ImageNet100-C dataset for the baseline MAE-TTT and for the modified MAE-TTT with 1, 2, and 3 entropy-minimization steps. The results demonstrate that adding these steps significantly improves performance.

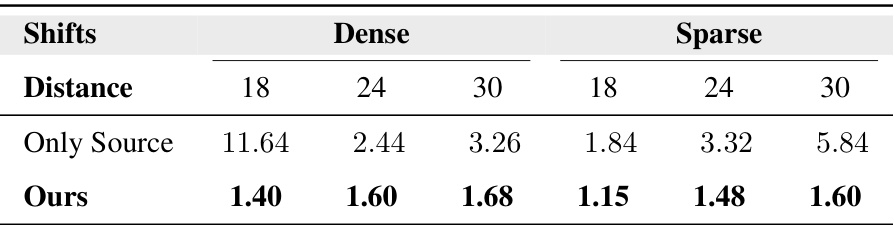
This table presents the Mean Squared Error (MSE) results of a regression task performed on synthetic data under different shift conditions (dense and sparse). The results are compared for three different out-of-support distances (18, 24, and 30), showing the performance of a model trained only on source data versus the proposed model. It demonstrates the effectiveness of the model in handling extrapolation under both dense and sparse shift scenarios and different levels of out-of-distribution data.

This table presents the results of synthetic data experiments on classification, comparing the test accuracy of three different methods: ‘Only Source’ (a model trained only on source data), iMSDA (an existing domain adaptation method), and the proposed method. The experiments were conducted under both ‘dense shifts’ (global transformations affecting all pixels) and ‘sparse shifts’ (local changes affecting only a subset of pixels). The accuracy is reported across different levels of ‘distance’ of the target sample from the source support, which represents the severity of distribution shift. The results show that the proposed method outperforms the baselines across all conditions, validating its ability to handle extrapolation effectively.

This table compares the test accuracy of different methods on the ImageNet-C dataset, which evaluates the robustness of models to various corruptions. It shows the performance of the proposed method compared to a baseline MAE-TTT and other baselines (Joint Train, Fine-Tune, ViT Probe). The average accuracy across all corruption types, along with individual results for each corruption type, are provided.

This table presents the results of synthetic data experiments conducted to validate the theoretical findings of the paper. The experiments involved binary classification tasks with varying levels of ‘dense’ and ‘sparse’ shifts in the data distribution. The accuracy of the model is evaluated across a range of distances between the target sample and the source distribution support. The results showcase how the model’s performance is affected by the nature of the shift (dense vs. sparse) and the distance of the target sample from the source distribution support.

Full paper

#