Exploring Fixed Point in Image Editing: Theoretical Support and Convergence Optimization

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in image editing and generation because it provides a rigorous theoretical foundation for a widely used method (DDIM inversion) and offers practical improvements to its performance. Its findings on fixed points and optimized loss functions can significantly impact the visual quality of edited images. The extension to unsupervised dehazing also opens new avenues for research in related areas.

Visual Insights

#

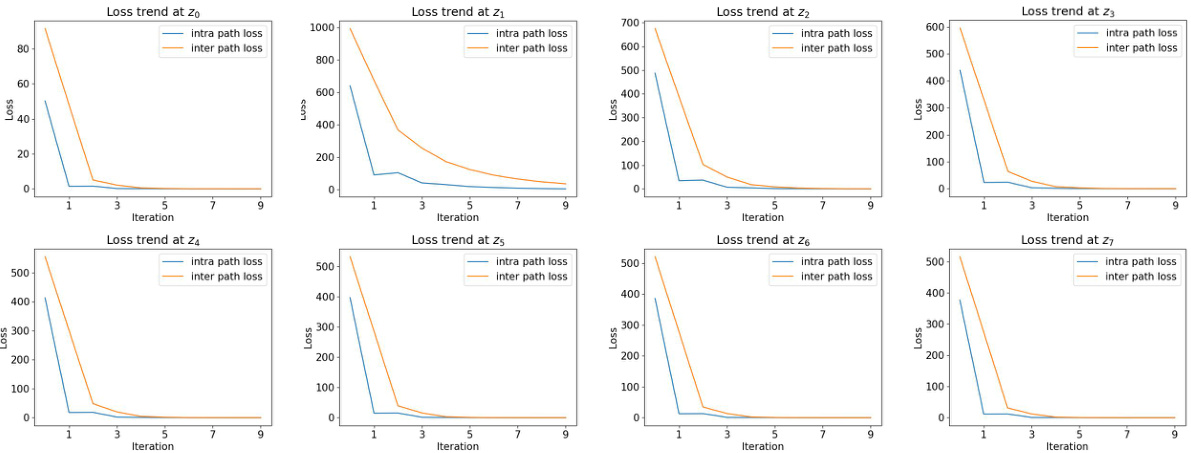
The figure shows the loss trend during the fixed-point iteration process in DDIM inversion for 8 time steps. Two loss functions are compared: the intra-path loss (f(zt) - zt) used in previous methods and a novel inter-path loss (f(zt) - f(zt)). The intra-path loss converges quickly, while the inter-path loss shows a noticeable delay. This highlights that the convergence of the intra-path loss doesn’t guarantee convergence to the true fixed point, emphasizing the importance of the novel inter-path loss for accurate fixed-point convergence.

This table presents the quantitative results of image editing and reconstruction experiments using three different methods: the original Prompt-to-Prompt (P2P) method, the fixed-point method (f(zt)-zt), and the optimized fixed-point method (f(zt)-f(zt)). Seven metrics across three dimensions (Structure, Background Preservation, and CLIP Similarity) are used to evaluate the performance. The metrics include Distance, PSNR, LPIPS, MSE, SSIM, Whole, and Edited. Bold values highlight the best performance for each metric.

In-depth insights

#

Fixed-Point Theory

#

The concept of “Fixed-Point Theory” within the context of iterative processes, particularly in the paper’s application to image editing via diffusion models, centers on identifying a stable equilibrium point within an iterative algorithm. The existence and uniqueness of such a fixed point is crucial, providing theoretical grounding for the iterative refinement process. The paper likely leverages the Banach fixed-point theorem, demonstrating that under certain conditions (e.g., the iterative function being a contraction mapping), a unique fixed point is guaranteed to exist, regardless of the starting point. The implications are significant: it guarantees convergence of the iterative algorithm towards a consistent, stable image reconstruction or editing result. Furthermore, understanding the theoretical properties of this fixed point informs the design of loss functions and optimization strategies, leading to enhanced convergence rates and improved image quality. The analysis likely delves into the Lipschitz constant of the iterative function, directly impacting the convergence speed and the stability of the overall process. This theoretical foundation is fundamental to justifying the practical efficacy of the image editing approach presented in the research.

DDIM Inversion

#

DDIM (Denoising Diffusion Implicit Models) inversion is a crucial technique in image editing, enabling the manipulation of images by reversing the diffusion process. It leverages the deterministic nature of DDIM sampling, framing it as a reversible ODE (Ordinary Differential Equation) process. This reversibility is key, allowing for the prediction of noise corresponding to a reference image. The core idea is to maintain consistency between the restored image and the reference; modifications to the noise are directly reflected in the final edited image. However, a primary challenge is the approximation error introduced by using the t-1 timestep to estimate noise at timestep t. This error accumulates, potentially leading to inconsistencies between the reference and the restored image. Recent work addresses this by formulating the inversion process as a fixed-point problem of an implicit function, but lacks theoretical justification for the existence of such points. This is a critical gap, as the existence and uniqueness of the fixed point are fundamental to the accuracy and reliability of the entire method. Consequently, theoretical proofs showing the existence and uniqueness of the fixed points under specific conditions are important. Furthermore, optimizing the loss function based on these theoretical insights is essential to improve the quality of image editing and enhance visual fidelity of edited images.

Convergence Analysis

#

A rigorous convergence analysis is crucial for evaluating the effectiveness and reliability of any iterative algorithm. In the context of the provided research paper, a thorough convergence analysis would ideally involve several key aspects. First, it should establish the existence of a fixed point towards which the iterative process converges. This often requires proving that the iterative map is a contraction, satisfying a Lipschitz condition with a contraction factor less than 1, or employing alternative fixed-point theorems. Second, the rate of convergence should be analyzed. Is it linear, quadratic, or sublinear? A faster convergence rate implies fewer iterations to reach a desired level of accuracy, which is critical for computational efficiency. Third, the analysis should investigate the impact of various parameters (e.g., step size, initial conditions) on the convergence behavior. Sensitivity to initial conditions indicates robustness and the overall reliability of the algorithm. Fourth, the analysis should carefully consider potential issues like stagnation, oscillations, or divergence under certain conditions. Identifying conditions that lead to these issues is crucial for improving the algorithm’s stability. Finally, the theoretical analysis should be validated through empirical evidence, demonstrating that the observed convergence behavior in experiments aligns with the theoretical predictions. A comprehensive convergence analysis should offer a detailed understanding of the algorithm’s behavior, informing design choices and improving its overall performance and applicability.

Dehazing Application

#

The paper explores applying its novel fixed-point-based image editing method to the task of unsupervised image dehazing. This is a significant extension, moving beyond supervised image editing to a more challenging, real-world problem. The core idea involves using the DDIM inversion process to remove haze by replacing the textual representation of ‘haze’ with a null-text embedding. This text-based approach cleverly avoids the need for paired hazy/clean image datasets, a common limitation in unsupervised dehazing. However, a key challenge addressed is the potential for image collapse when using this null-text approach. The authors demonstrate that incorporating their optimized fixed-point approach mitigates this issue, leading to improved results. The effectiveness is evaluated on the RESIDE dataset, comparing results to other methods that lack fixed-point optimization. While the results show promise, the authors acknowledge limitations, particularly regarding the imperfect alignment of attention maps and the generation of artifacts. Future work will focus on refining this text-based approach to further enhance dehazing performance and address these remaining challenges.

Future Directions

#

Future research should focus on extending the theoretical framework to encompass more complex diffusion models and handle scenarios with noisy or incomplete data. Improving the efficiency of fixed-point solvers is crucial, especially for high-resolution images, where computational cost can be prohibitive. Investigating the impact of different noise schedules and diffusion model architectures on the convergence properties of fixed-point iterations is also important. Furthermore, exploring the application of fixed-point based methods in other image restoration tasks, such as image inpainting, super-resolution, and colorization, would be a valuable contribution. A crucial area for future work involves addressing the limitations of unsupervised image dehazing by enhancing the accuracy and robustness of the haze removal process. Finally, thorough investigation into the ethical implications of advanced image editing techniques is necessary to mitigate potential misuse and ensure responsible development.

More visual insights

#

More on figures

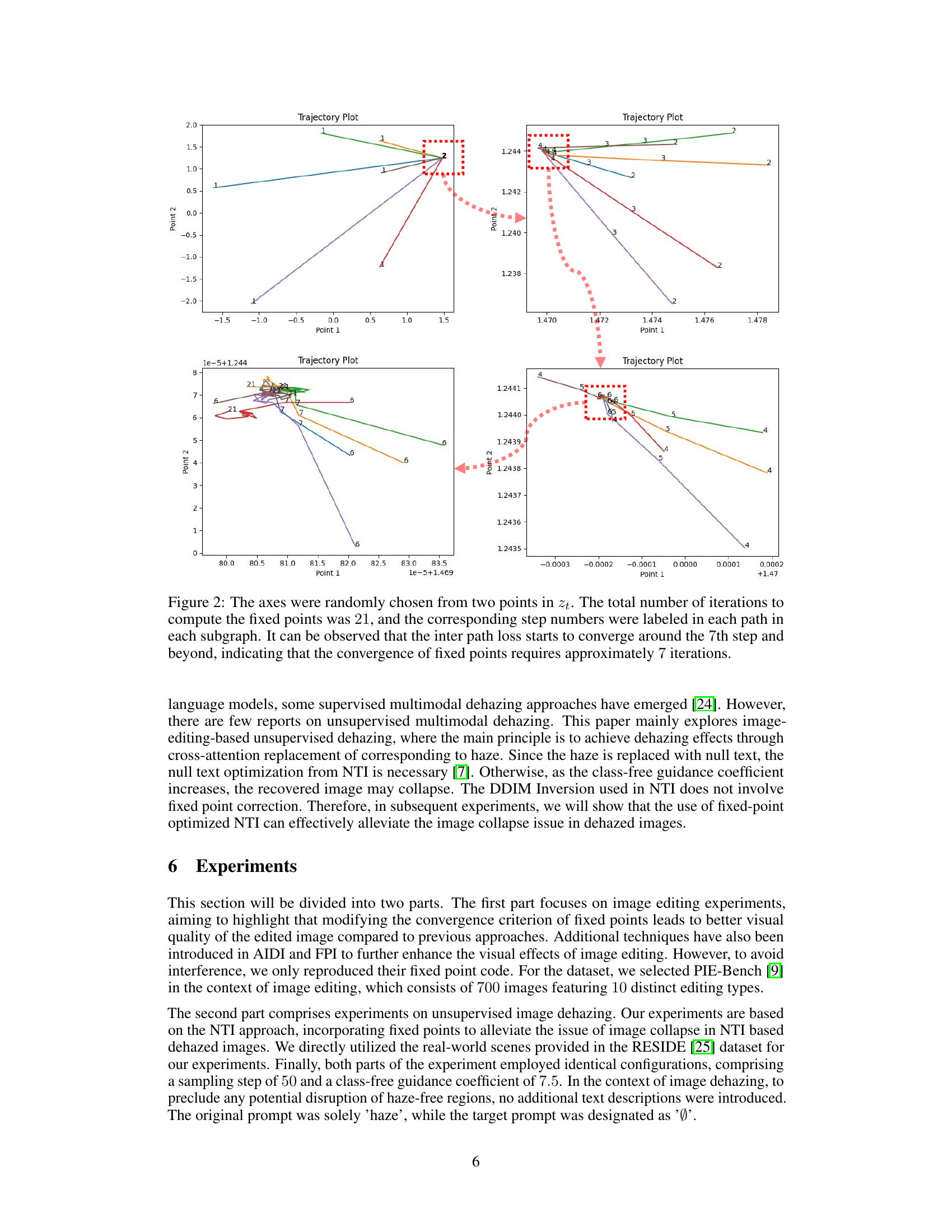
This figure shows the convergence behavior of the fixed-point loss during the DDIM inversion process. Multiple trajectories are plotted, each starting from a different point, to visualize the convergence to a unique fixed point. The plots illustrate that the convergence of the inter-path loss, representing the difference between the function values at two points, lags behind the intra-path loss (difference between function value and point value), demonstrating the need for optimizing the convergence criterion.

This figure shows the image editing results using three different methods: P2P, the original fixed-point method (f(zt) - zt), and the proposed optimized fixed-point method (f(zt) - f(zt)). Each row presents a different image editing task, with the original image, the P2P edited image, the result using f(zt) - zt, and the result using f(zt) - f(zt). The prompts used for editing are also given. The figure demonstrates the improvement in image quality achieved with the proposed optimization.

This figure shows a comparison of image editing results using three different methods: the original Prompt-to-Prompt (P2P) method, the P2P method with the intra path loss (f(zt) − zt), and the P2P method with the optimized inter path loss (f(zt) − f(zt)). The results demonstrate that using the optimized inter path loss leads to better visual quality and more consistent results compared to the other methods. Each row represents a different image editing task, with the original image on the left and the results of the three methods displayed in subsequent columns.

This figure shows the results of image dehazing using four different methods: Input (original hazy images), NTI (Null-text Inversion), NTI w Fixed Point (NTI with fixed-point optimization), and Fixed Point w/o NTI (fixed-point optimization without NTI). The bottom row displays the corresponding haze attention maps for each image. The figure demonstrates the effectiveness of incorporating fixed-point optimization in mitigating image collapse issues observed in unsupervised dehazing, especially when NTI is not used.

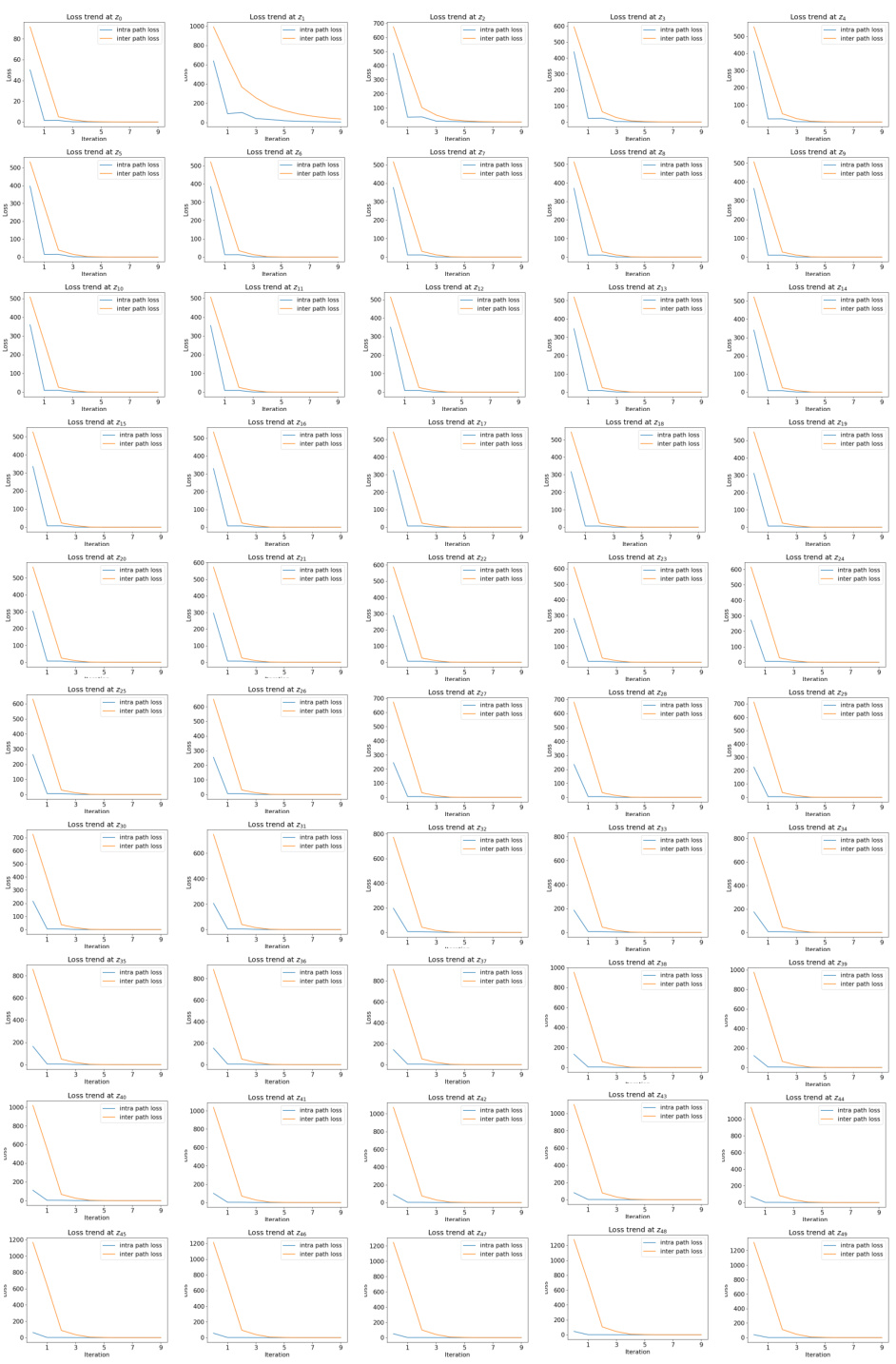
This figure shows the loss trend during the iterative process of finding fixed points in DDIM inversion. Two loss functions are compared: the intra-path loss (f(zt) - zt) used in previous methods (AIDI and FPI), and the proposed inter-path loss (f(zt) - f(zt)). The figure demonstrates that while the intra-path loss converges quickly, the inter-path loss shows a significant lag. This highlights that the convergence of the intra-path loss alone is insufficient to guarantee the convergence of fixed points, and emphasizes the importance of using the inter-path loss as a criterion for convergence.

This figure shows a comparison of image editing results using three different methods: the original Prompt-to-Prompt (P2P) method, the P2P method with the intra-path loss (f(zt) − zt), and the P2P method with the optimized inter-path loss (f(zt) − f(zt)). The results demonstrate that optimizing the convergence of fixed points (using the inter-path loss) leads to a significant improvement in the visual quality of edited images. Several examples of image edits are displayed, showcasing the effects of each method.

This figure shows the convergence of fixed points in the DDIM inversion process. Four subplots display trajectory plots illustrating how iterations converge towards a fixed point. Each trajectory represents the iterative process from an initial point toward the fixed point. The plots demonstrate that the proposed optimized loss function (inter path loss) converges more slowly than the original loss function (intra path loss). The convergence of the inter path loss indicates the actual convergence of fixed points, which takes around 7 iterations.

This figure shows the image editing results using three different methods: the original Prompt-to-Prompt (P2P) method, the P2P method with intra path loss (f(zt) − zt), and the P2P method with optimized inter path loss (f(zt) − f(zt)). The examples demonstrate how the optimized inter path loss leads to improved visual quality in image editing by better preserving details and consistency.

This figure shows the image editing results of using three different methods: P2P, the original fixed-point method (f(zt) − zt), and the optimized fixed-point method (f(zt) − f(zt)). Each row shows the results for a different image editing task, with the original image on the far left, followed by results from each method. The prompts used for each editing task are also shown. The figure illustrates that the proposed optimized method provides improved image quality, specifically better preservation of the original image and more reliable editing.

This figure shows the results of image editing experiments using the PIE-Bench dataset. The figure compares results from three different methods: the original P2P method, P2P with the original fixed-point loss function (f(zt) - zt), and P2P with the optimized fixed-point loss function (f(zt) - f(zt)). Each row shows a different image editing task, demonstrating that the optimized loss function produces better visual quality than the original methods.

This figure shows several examples of image editing results using the PIE-Bench dataset. Each row presents an original image, the results of using the P2P method, the results using the f(zt) - zt loss function, and finally the results using the optimized f(zt) - f(zt) loss function. The images demonstrate changes made based on different text prompts, highlighting the effects of each editing method on image quality and consistency.

This figure shows the results of image editing experiments performed using the PIE-Bench dataset. It visually compares the results obtained using three different methods: the original Prompt-to-Prompt (P2P) method, the P2P method with the fixed-point loss function (f(zt) - zt), and the optimized P2P method with the improved fixed-point loss function (f(zt) - f(zt)). Each row represents a different image editing task, illustrating how each method affects the image. The figure showcases various image manipulations, highlighting the effectiveness of the proposed optimization in terms of visual quality and consistency.

This figure shows a comparison of image dehazing results using different methods. The class-free guidance coefficient is set to 1. The top row shows successful dehazing, where the red boxes highlight areas where details are improved. The bottom row shows unsuccessful dehazing, where the red boxes show how the methods negatively impact certain features. This illustrates that the use of fixed points in the image dehazing process is not universally beneficial and depends on the specific image characteristics.

Full paper

#