Dendritic Integration Inspired Artificial Neural Networks Capture Data Correlation

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it bridges the gap between biological neural mechanisms and artificial neural networks. By incorporating quadratic integration rules observed in biological dendrites, it offers a novel approach to enhance the performance and generalization capabilities of CNNs. This opens up exciting new avenues for research in biologically-inspired AI and could lead to more efficient and powerful AI models.

Visual Insights

#

This figure compares the decision boundaries of a single quadratic neuron and a two-layer Multilayer Perceptron (MLP) for two binary classification tasks with varying numbers of training samples. The left side shows results for a task where the two classes have identical covariance matrices, while the right side depicts a task with non-identical covariance. The plots show that the quadratic neuron converges to the theoretically optimal boundary much faster (with fewer training examples) than the MLP, especially in the more challenging task (non-identical covariance). This highlights the advantage of quadratic neurons in capturing correlations within the data.

This table summarizes existing works that utilize quadratic formats in neural networks. It compares different approaches based on how the quadratic operation is used (pixel-wise or channel-wise), whether there is a biological interpretation to support the approach, and whether there is a theoretical basis for its generalization capabilities. The Dit-CNNs proposed in this paper are included for comparison.

In-depth insights

#

Quadratic Neuron Theory

#

The hypothetical “Quadratic Neuron Theory” proposes a significant departure from traditional artificial neural networks (ANNs) by substituting the linear summation of synaptic inputs with a quadratic integration rule. This non-linearity, inspired by biological observations of dendritic integration, is argued to inherently capture data correlations. This is a crucial advantage as it potentially reduces the need for extensive training data, improving generalization capabilities and making the model more robust. The theory suggests that quadratic neurons can effectively capture covariance relationships within structured data, a property demonstrated through binary and multi-class classification tasks on datasets with normally distributed data. Mathematical proofs support the claim that quadratic neurons converge to optimal solutions, unlike their linear counterparts, highlighting a superior learning capacity. However, the assumption of normally distributed data presents a limitation that should be addressed in future work. Despite this, the theoretical framework provides a compelling rationale for exploring quadratic neurons as a more biologically plausible and computationally efficient approach to building powerful and generalizable ANNs.

Dit-CNN Architecture

#

The Dit-CNN architecture represents a novel approach to convolutional neural networks (CNNs) by integrating quadratic neurons inspired by the dendritic integration rules observed in biological neurons. This integration enhances the CNN’s ability to capture correlations within structured data, a key advantage over traditional linear CNNs that simply sum inputs. The core innovation lies in incorporating a biologically plausible quadratic integration term into the convolutional operations, enabling the network to better discern relationships between different channels or input features. Dit-CNNs achieve this by adding a quadratic term based on the dendritic quadratic integration rule, which can be computed efficiently, resulting in improved accuracy and generalization performance. The quadratic term allows the network to capture higher-order interactions between input features, leading to a more nuanced representation of the data and a substantial improvement in classification accuracy, particularly in few-shot learning scenarios and high-dimensional datasets. This architecture strikes a balance between biological plausibility and computational efficiency, offering a powerful enhancement to the traditional CNN paradigm.

ImageNet-1K Results

#

ImageNet-1K, a large-scale visual recognition benchmark, presents a challenging testbed for evaluating the performance of deep learning models. The results section on ImageNet-1K would likely detail the accuracy (top-1 and top-5) achieved by the proposed Dit-CNNs, comparing them against existing state-of-the-art models. Crucially, the analysis would focus on the efficiency gains, demonstrating how the incorporation of quadratic neurons, inspired by biological dendritic integration, provides performance boosts without a significant increase in computational complexity or model parameters. A detailed breakdown of results across different ConvNeXt model sizes (T, S, B) would further showcase the scalability of this approach. Successful results would validate the effectiveness of quadratic neurons in capturing data correlation and potentially highlight improved generalization abilities compared to traditional linear models. Finally, the discussion may emphasize the biological plausibility of the architecture and its potential for future research directions in biologically-inspired deep learning.

Computational Cost

#

The computational cost of incorporating quadratic neurons is a significant concern. While enhancing accuracy, the added complexity of quadratic integration compared to linear methods increases the number of parameters and computations. The paper addresses this by strategically integrating quadratic neurons into only a few layers of the network, mitigating the overall performance impact. However, future research should explore more efficient implementations, perhaps by leveraging the inherent sparsity observed in biological dendritic structures to reduce computational burden. Analyzing the scalability of the approach to larger networks and datasets is also crucial, as the quadratic complexity could become a limiting factor for very large-scale problems. Further investigation into optimized hardware or algorithmic solutions to accelerate quadratic operations is also needed to unlock the full potential of this promising technique without significant performance trade-offs.

Future Research

#

Future research directions stemming from this work on quadratic neural networks could explore several key areas. Extending the theoretical framework beyond normally distributed data is crucial for broader applicability. Investigating the impact of different quadratic integration rules and their biological plausibility on various network architectures is important. Furthermore, exploring optimal strategies for integrating quadratic neurons within larger, more complex models is necessary to fully leverage their potential. Addressing the computational cost associated with quadratic neurons, perhaps through sparsity-inducing techniques, is also a critical consideration. Finally, a deeper investigation into the connection between quadratic neurons and other high-order interaction methods would provide valuable insights into their relative strengths and weaknesses. This includes a thorough exploration of the generalization performance of quadratic neurons under various data conditions and their potential applications beyond the computer vision tasks explored here.

More visual insights

#

More on figures

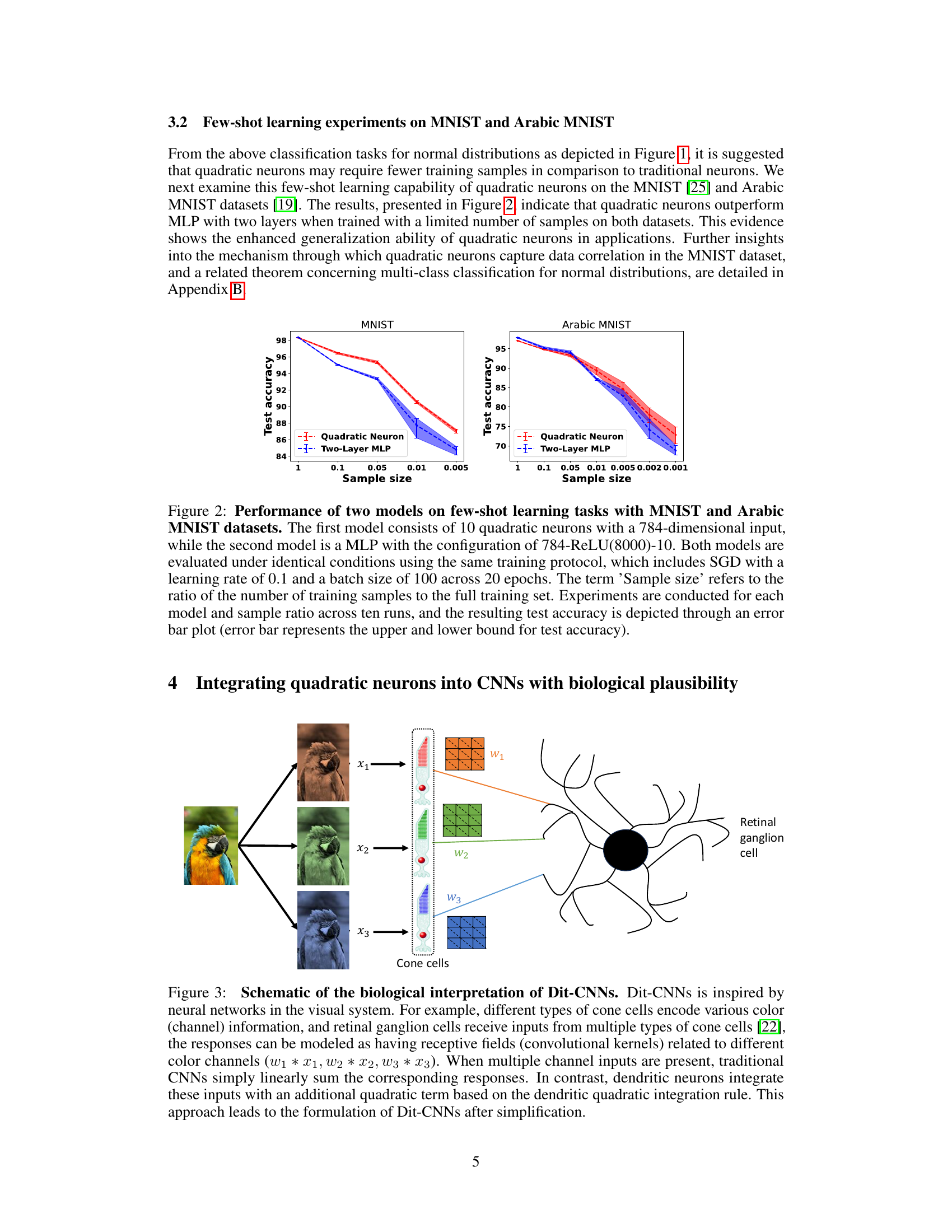
The figure shows the performance comparison of two models (quadratic neuron model and two-layer MLP) on few-shot learning tasks using MNIST and Arabic MNIST datasets. The results demonstrate that the quadratic neuron model outperforms the two-layer MLP, especially when trained with limited samples. The graph plots test accuracy against the sample size (the ratio of training samples to the whole training set).

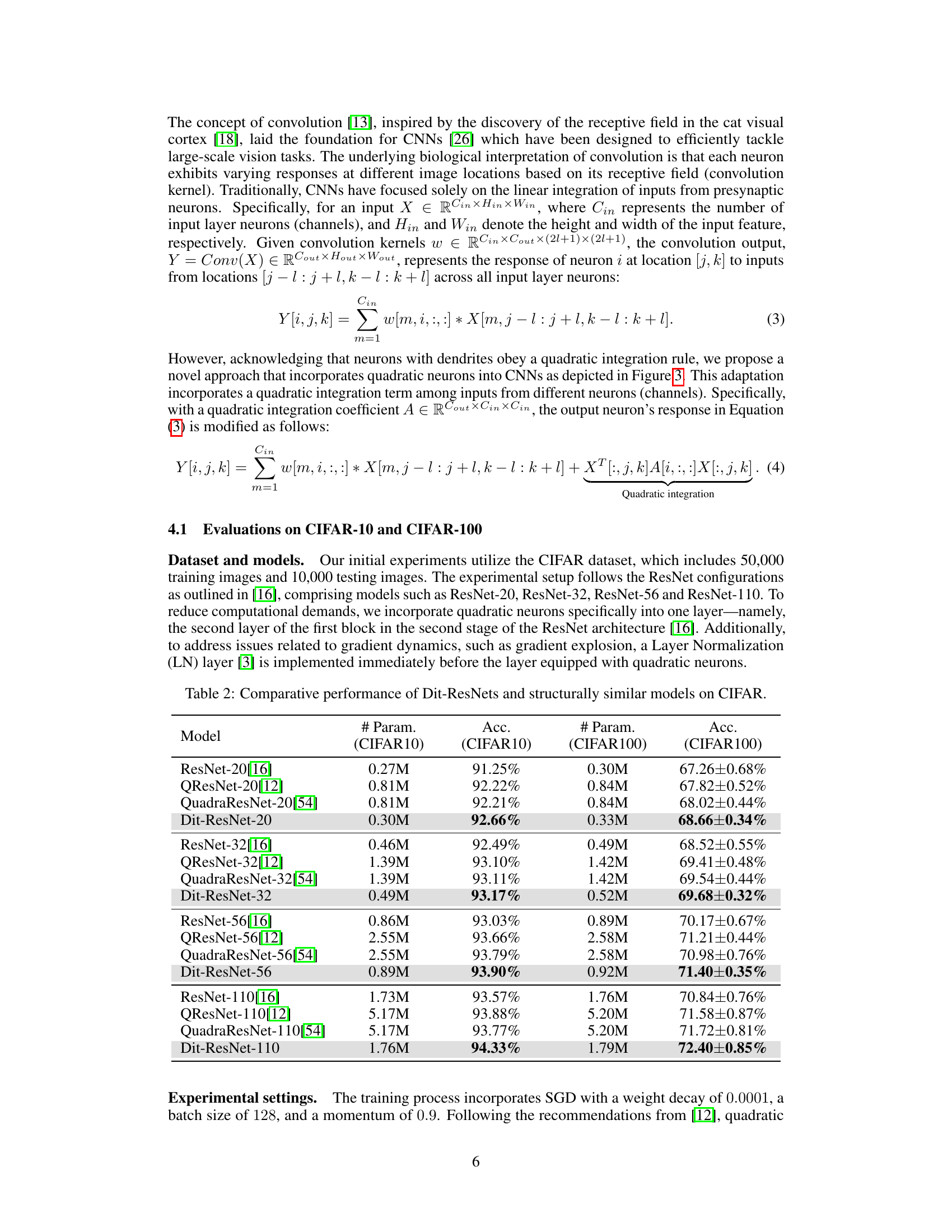
This figure illustrates how Dit-CNNs are inspired by the biological visual system. Different cone cells process different color channels, sending signals to retinal ganglion cells. Traditional CNNs sum these signals linearly, but Dit-CNNs add a quadratic term reflecting dendritic integration, leading to their unique architecture.

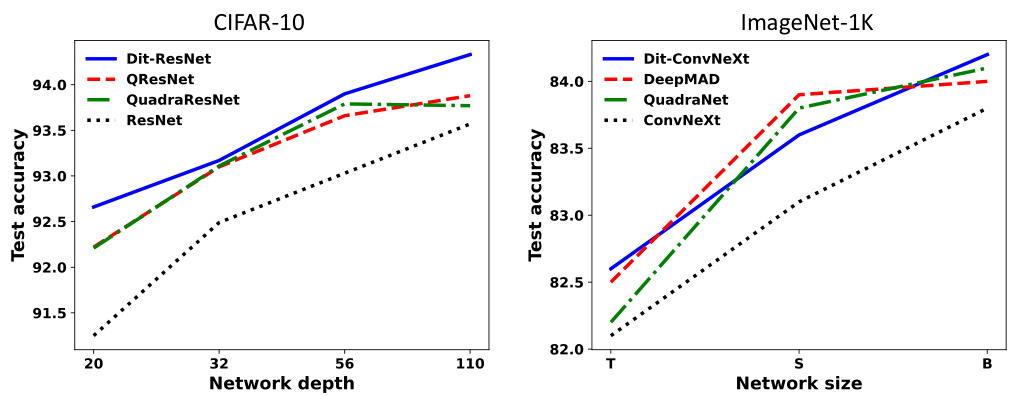
This figure visualizes the performance results from Tables 2 and 3. The left panel shows the test accuracy of different ResNet models (ResNet, Dit-ResNet, QResNet, QuadraResNet) on CIFAR-10, plotted against network depth. The right panel displays the top-1 accuracy of various ConvNeXt models (ConvNeXt, Dit-ConvNeXt, DeepMAD, QuadraNet) on ImageNet-1K, plotted against network size. The Dit-CNN models consistently show improved performance compared to the baselines across both datasets.

This figure shows the architecture of ConvNeXt with three candidate layers highlighted in red where quadratic neurons were integrated. The right panel shows the ImageNet-1k performance comparison between original Dit-ConvNeXt-T and Dit-ConvNeXt-T after removing the quadratic term. The results demonstrate that the quadratic term significantly contributes to improved accuracy, particularly in Block 3.

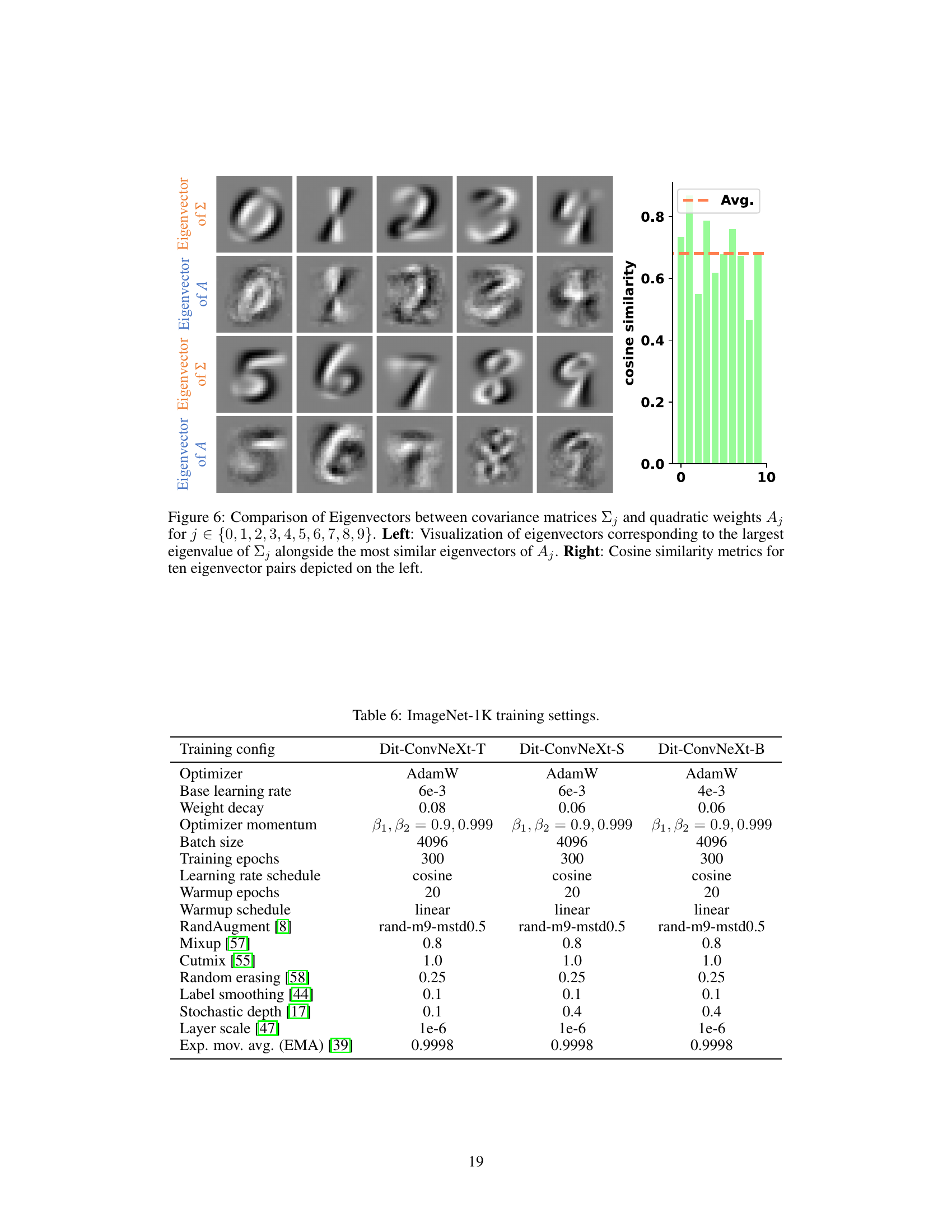
This figure compares eigenvectors from covariance matrices (Σj) and quadratic weights (Aj) for each digit class (0-9) in the MNIST dataset. The left panel visualizes these eigenvectors, showing a strong similarity between those from Σj (representing data distribution) and Aj (learned by quadratic neurons). The right panel quantifies this similarity using cosine similarity, demonstrating that quadratic neurons effectively capture data correlations inherent in the MNIST dataset.

More on tables

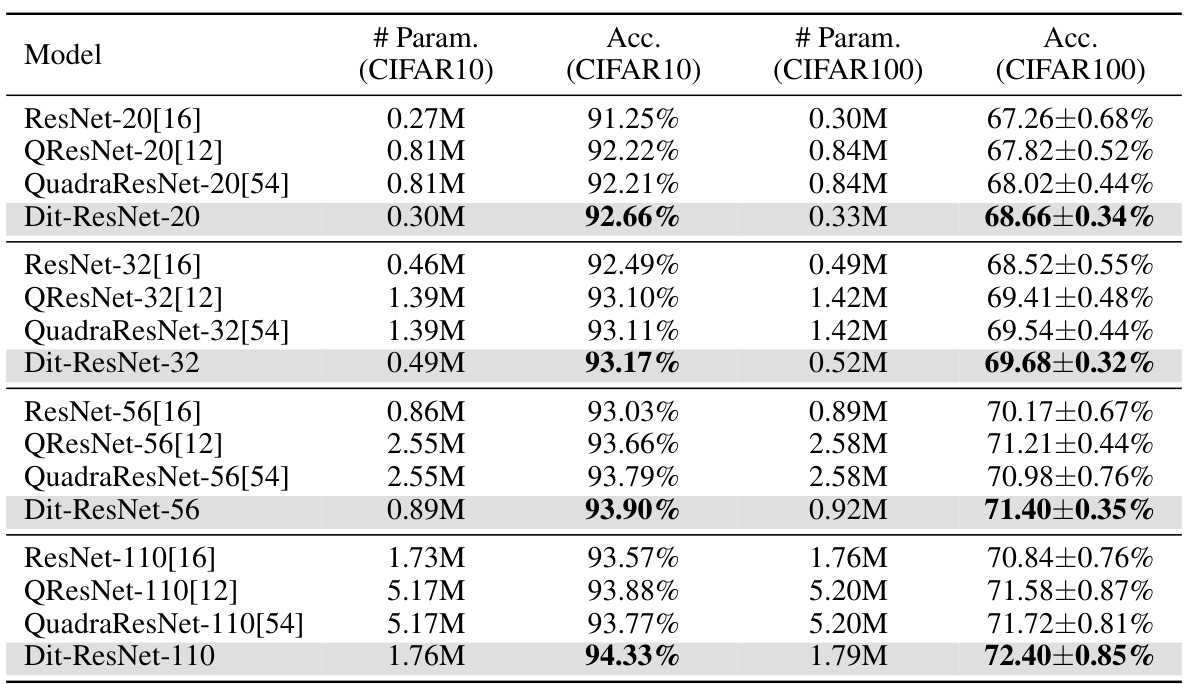
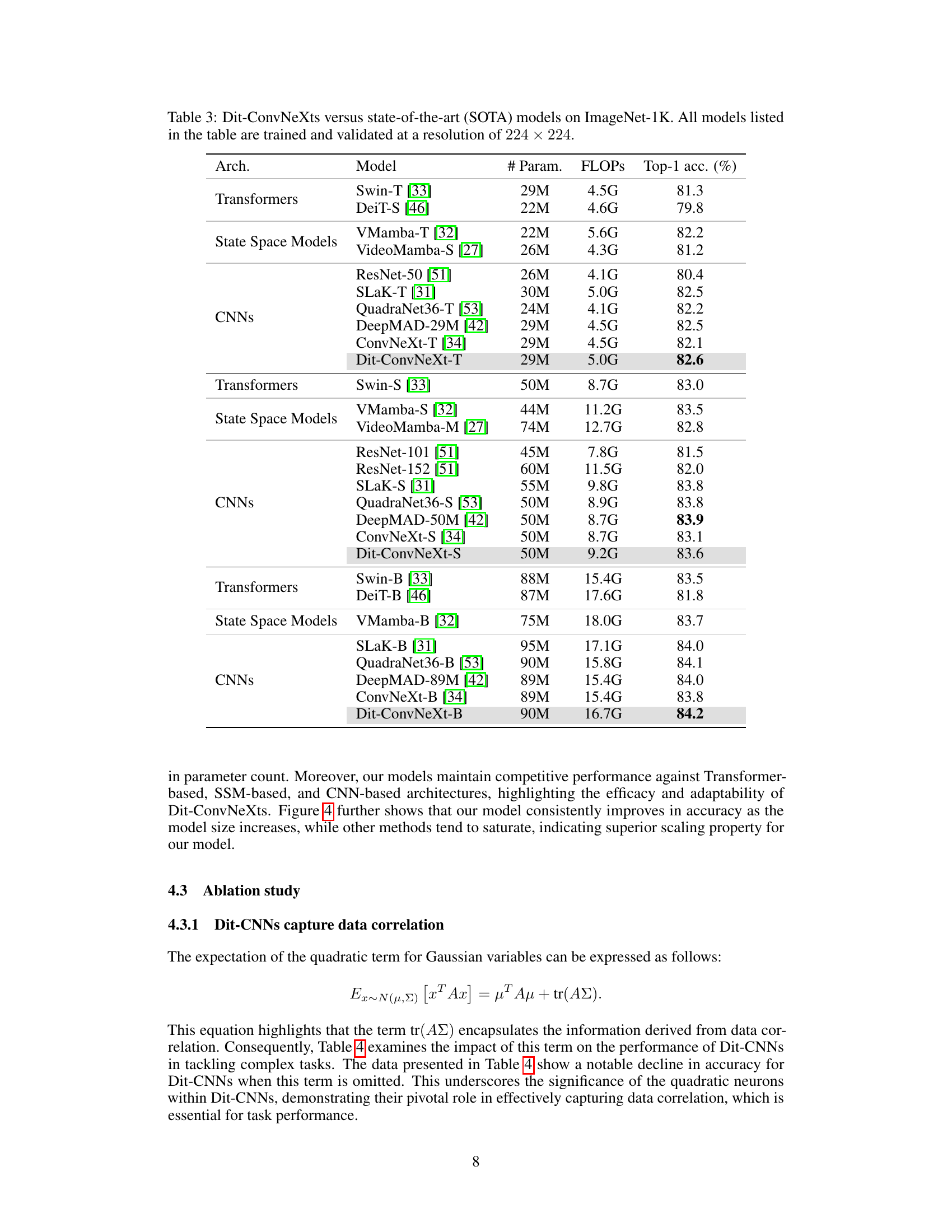
This table presents a comparison of the performance of Dit-ResNets (the proposed model) against standard ResNet models and other similar models that incorporate quadratic neurons, across different depths (20, 32, 56, 110) on CIFAR-10 and CIFAR-100 datasets. The comparison includes the number of parameters and the accuracy achieved. It shows that the Dit-ResNets achieve higher accuracy with fewer parameters, highlighting the effectiveness of the proposed approach.

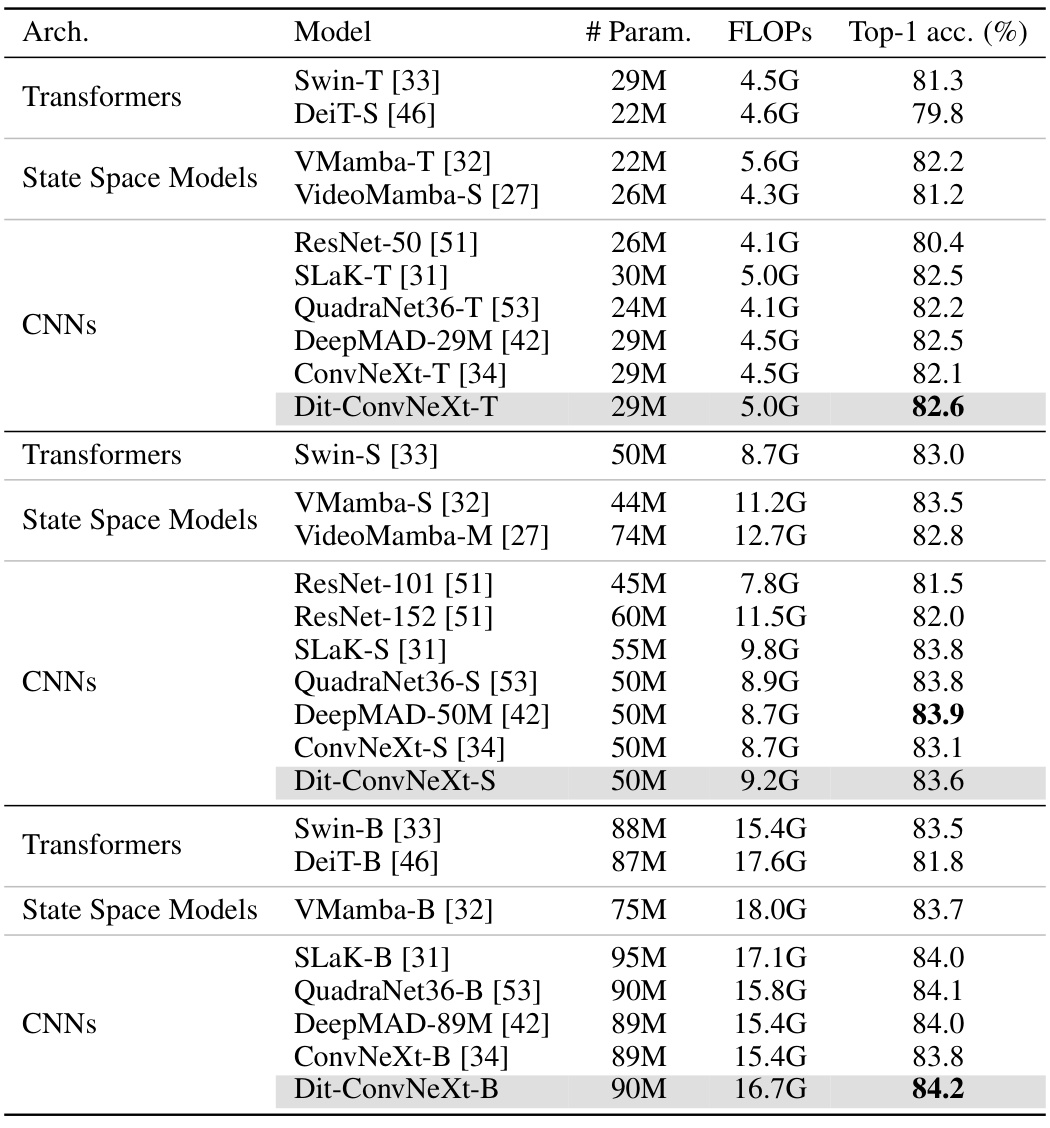
This table compares the performance of Dit-ConvNeXt models (proposed in the paper) against other state-of-the-art (SOTA) models on the ImageNet-1K dataset. The comparison includes various architectural categories like Transformers, State Space Models, and CNNs. For each model, the number of parameters, FLOPs (floating point operations), and top-1 accuracy are provided. The results demonstrate the competitive performance of Dit-ConvNeXt models, achieving high accuracy with relatively efficient use of parameters and computational resources.

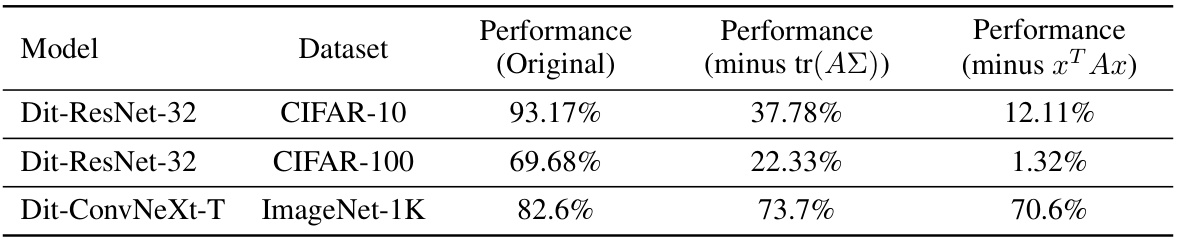
This table presents the performance comparison of Dit-CNNs (Dendritic Integration inspired CNNs) and their variations on three different datasets: CIFAR-10, CIFAR-100, and ImageNet-1K. The original Dit-CNNs’ performance is compared against two modified versions: one where the covariance term tr(ΑΣ) is removed and another where the quadratic term x^TAx is removed from the quadratic neurons. The results highlight the significant contribution of both terms, particularly the covariance term, to the overall performance of the Dit-CNN models.

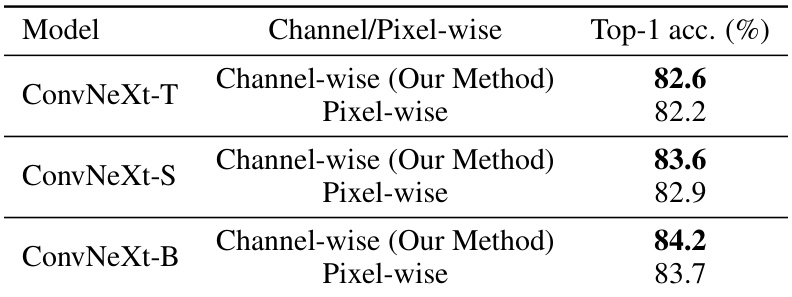
This table compares the performance of channel-wise and pixel-wise application of quadratic neurons in ConvNeXt models of various sizes (T, S, B). The results demonstrate that the channel-wise application of quadratic neurons, as proposed in the Dit-CNN architecture, yields significantly higher top-1 accuracy on ImageNet-1K compared to the pixel-wise approach.

This table presents a comparison of the performance of Dit-ResNets (the proposed model) and other similar models on CIFAR-10 and CIFAR-100 datasets. It shows the number of parameters, accuracy on CIFAR-10, and accuracy on CIFAR-100 for different ResNet models (ResNet-20, ResNet-32, ResNet-56, and ResNet-110), their quadratic counterparts from prior work (QResNet and QuadraResNet), and the proposed Dit-ResNet models. The results demonstrate the improved performance of Dit-ResNets in terms of accuracy while maintaining a similar number of parameters compared to the original ResNet models.

Full paper

#