↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Multi-agent cooperation, particularly in scenarios with misaligned individual and collective goals (mixed-motive), remains a significant challenge. Current approaches often rely on manual reward design or lack theoretical justification. This limits the generalizability and scalability of cooperative AI systems.
This paper tackles this challenge by introducing a novel optimization method called Altruistic Gradient Adjustment (AgA). AgA uses gradient adjustments to progressively align individual and collective objectives. The researchers theoretically prove its effectiveness and validate it empirically across various game environments, including a new large-scale environment called Selfish-MMM2. AgA demonstrates superior performance compared to existing methods, highlighting its potential for creating more effective and robust cooperative AI agents.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in multi-agent reinforcement learning, especially those working on mixed-motive cooperation. It introduces a novel optimization method, AgA, that effectively aligns individual and collective objectives, a long-standing challenge in the field. AgA’s theoretical grounding and empirical validation make it a significant contribution, opening new avenues for designing more effective collaborative AI agents. The introduction of the Selfish-MMM2 environment also provides a valuable benchmark for future research.
Visual Insights#

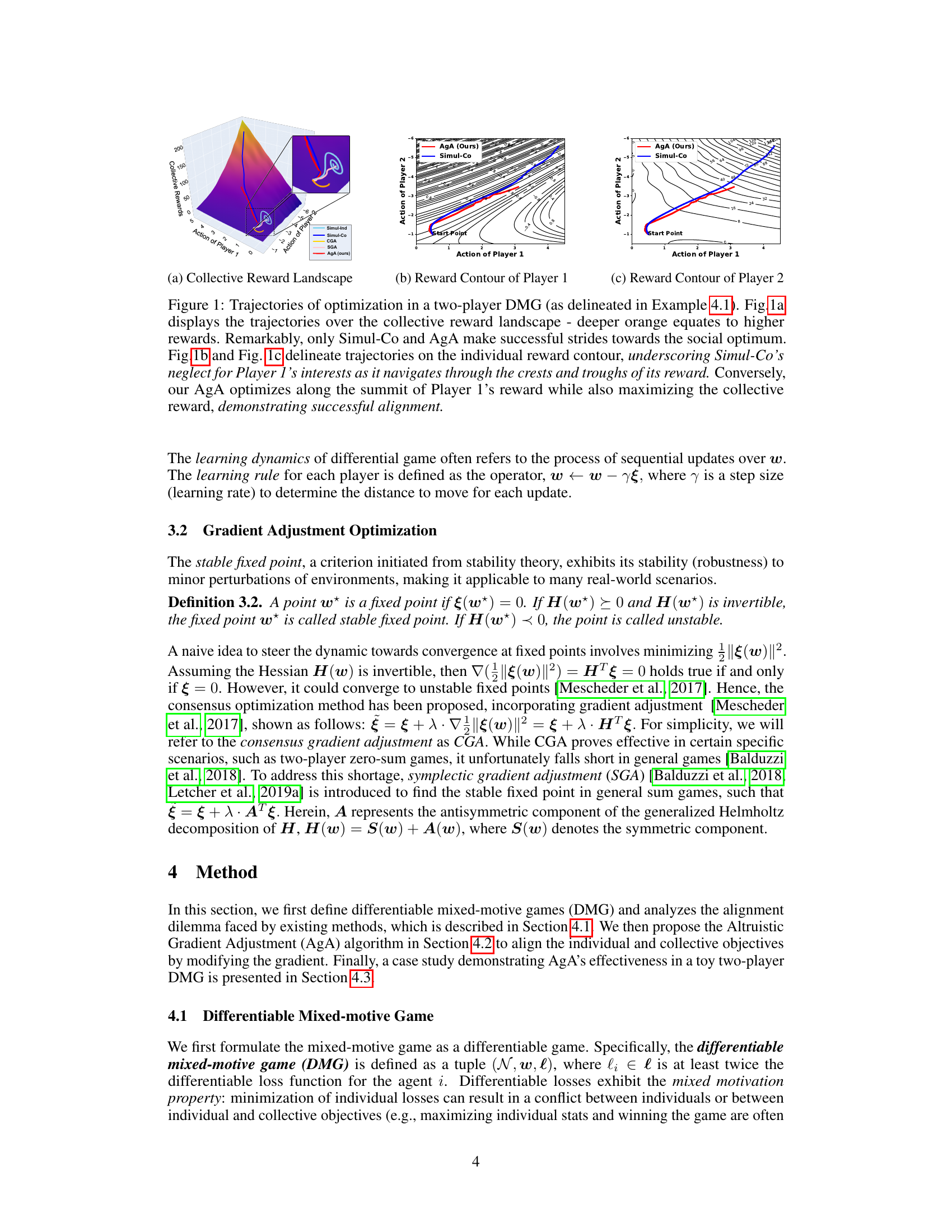
This figure shows the optimization trajectories of different algorithms in a two-player differentiable mixed-motive game. Panel (a) displays the collective reward landscape, illustrating how different methods approach the social optimum. Panel (b) and (c) show the individual reward contours for players 1 and 2, respectively, highlighting the differences in how the algorithms balance individual and collective objectives. AgA is shown to successfully align both objectives.

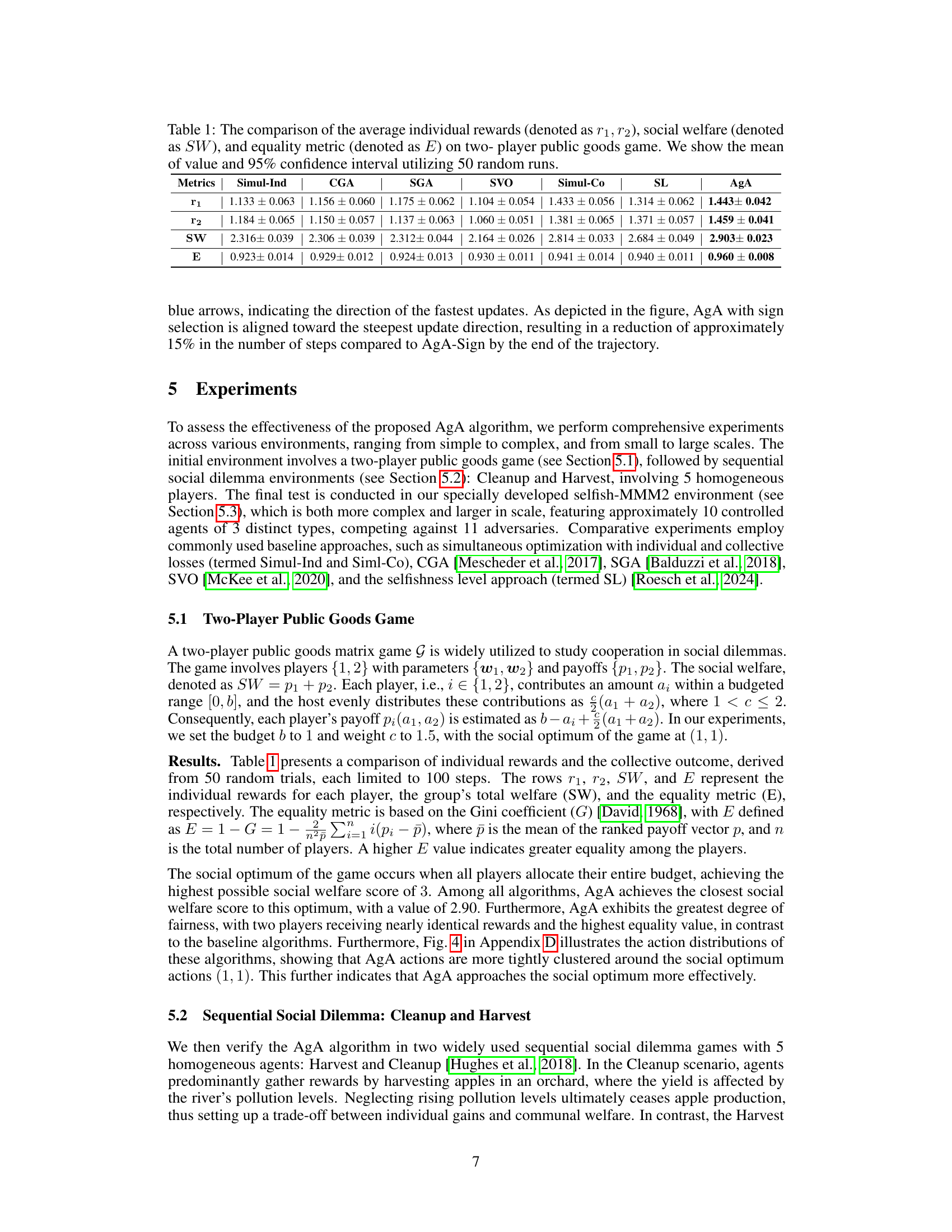
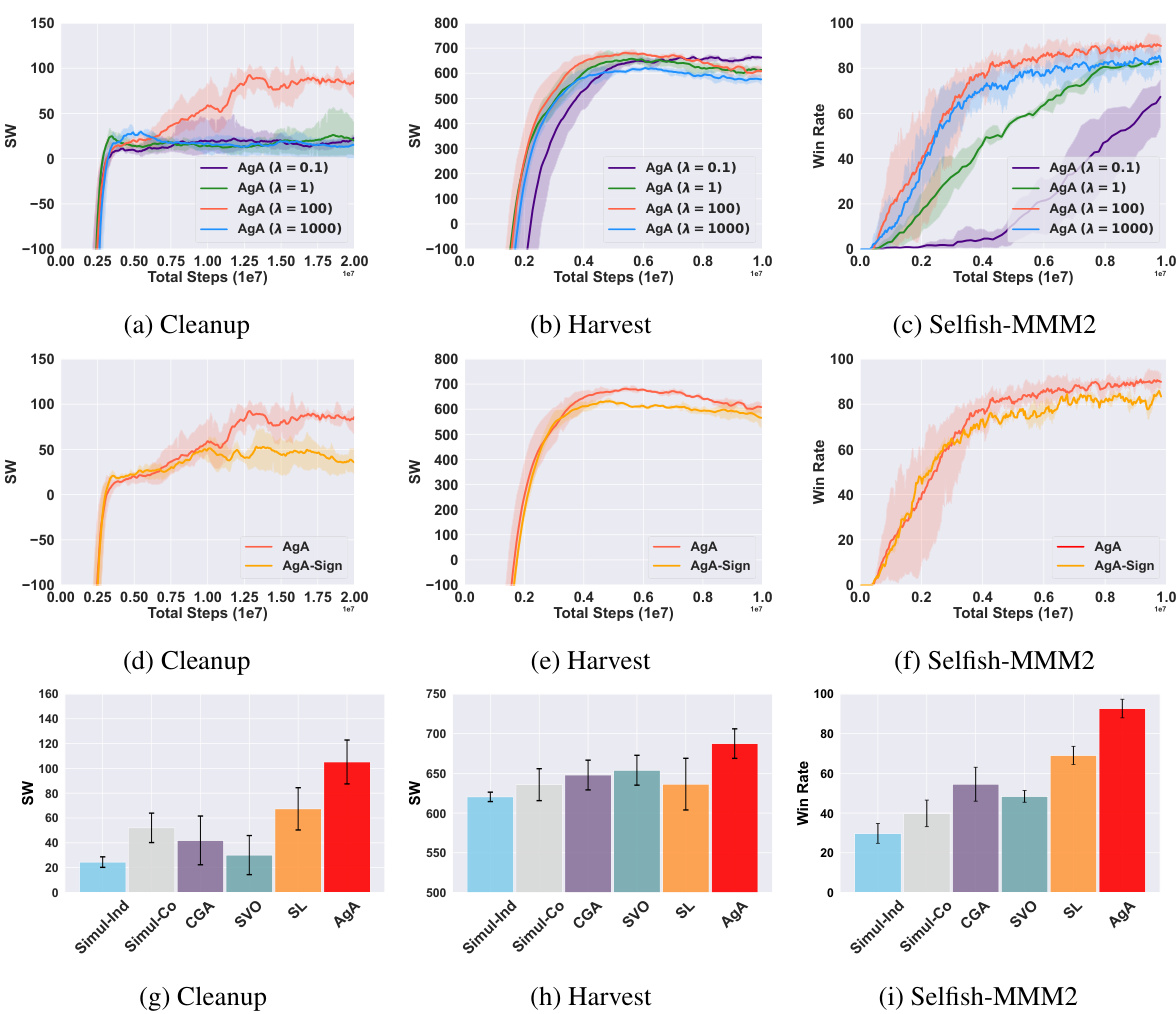
This table presents the results of a two-player public goods game experiment comparing seven different algorithms: Simul-Ind, CGA, SGA, SVO, Simul-Co, SL, and AgA. For each algorithm, the table shows the average individual rewards for player 1 (r1) and player 2 (r2), the social welfare (SW, the sum of individual rewards), and an equality metric (E, based on the Gini coefficient). The results are based on 50 random runs, and the table displays the mean and 95% confidence intervals for each metric.
In-depth insights#
Mixed-motive games#
Mixed-motive games are a fascinating area of game theory that explores scenarios where participants have both cooperative and competitive interests. Unlike pure-motive games where everyone benefits from collaboration, mixed-motive games present a complex interplay of individual gains and collective well-being. Understanding the dynamics of these games is crucial as they mirror numerous real-world situations—from international relations to social dilemmas. Strategies in mixed-motive games often involve balancing individual incentives with the need for collective action. The challenge lies in designing mechanisms that align these sometimes conflicting goals. Researchers investigate reward structures, communication protocols, and even social norms to facilitate cooperation. Game theoretic concepts like Nash equilibrium offer analytical frameworks, but these can be computationally demanding and may not capture the complexities of human or machine learning behavior. Studying mixed-motive games is vital for building more effective, robust, and ethical systems in multi-agent environments.
AgA Algorithm#
The core of this research paper revolves around the innovative Altruistic Gradient Adjustment (AgA) algorithm, designed to address the challenge of aligning individual and collective objectives within multi-agent cooperation. AgA’s ingenuity lies in its differentiable game framework, enabling a detailed analysis of learning dynamics towards cooperation. Unlike traditional methods focusing solely on individual or collective objectives, AgA dynamically adjusts gradients to effectively guide the system towards the stable fixed points of the collective objective, while simultaneously considering individual agent interests. This is achieved through a novel gradient modification technique that theoretically ensures convergence towards optimal collective outcomes while preventing neglect of individual needs. The algorithm’s effectiveness is rigorously validated across various benchmark environments, showcasing its adaptability and superior performance compared to established baselines. Theoretical proofs and extensive empirical results demonstrate AgA’s ability to effectively balance individual and collective interests, making it a significant contribution to the field of multi-agent learning and offering potential solutions for real-world collaborative scenarios.
Large-scale test#
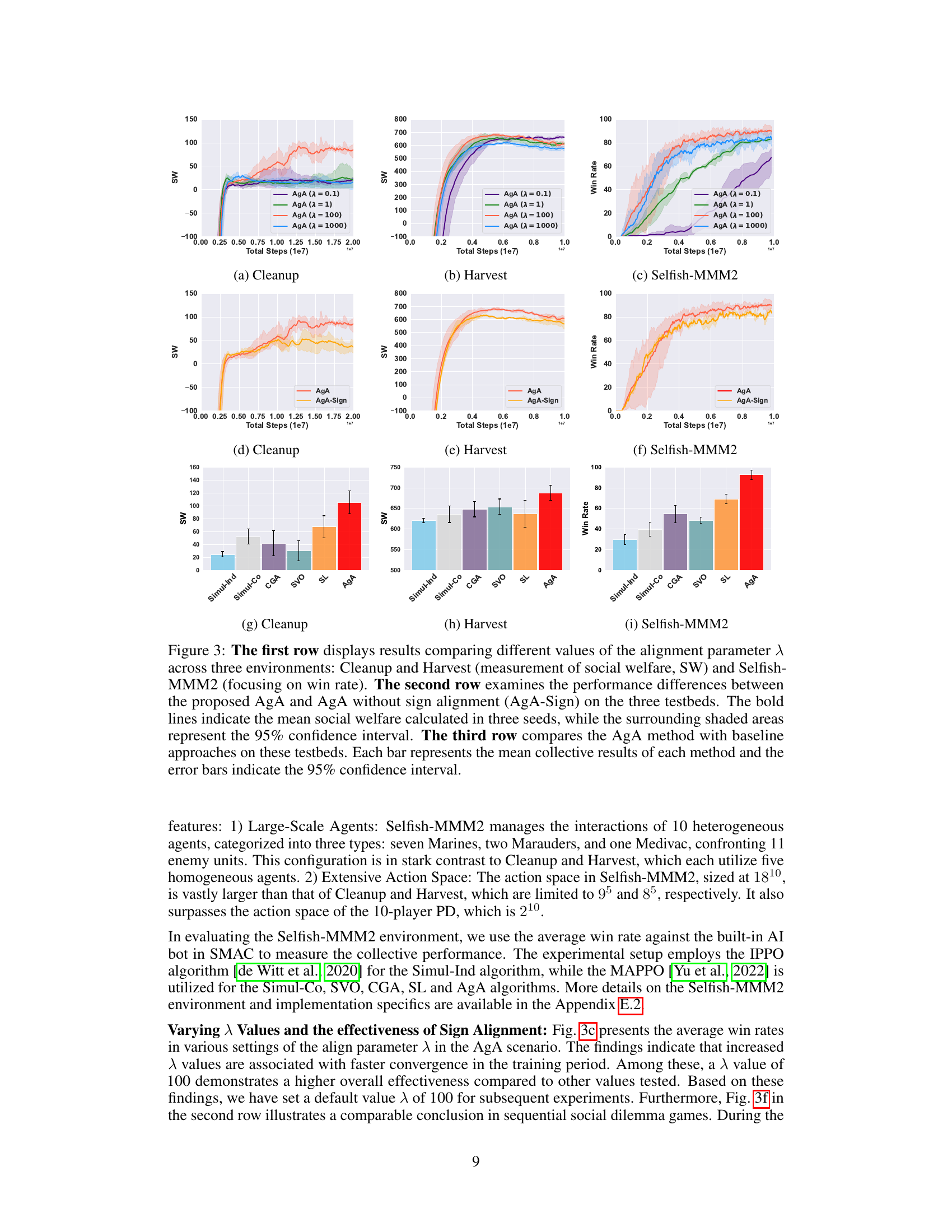
A large-scale test within the context of a multi-agent reinforcement learning research paper would likely involve evaluating the proposed algorithm in a complex environment with a substantial number of agents, actions, and interactions. This is crucial to assess the scalability and generalizability of the algorithm beyond smaller, more controlled settings. A well-designed large-scale test would consider the computational cost and complexity involved, potentially employing techniques such as distributed training or approximate methods to make the experiment feasible. The metrics used for evaluation in a large-scale test should also be carefully chosen, focusing on those that capture the essential aspects of multi-agent cooperation, such as overall performance, fairness, and robustness. Key aspects of a successful large-scale test include a thorough description of the environment, a clear definition of the evaluation metrics, and a robust analysis of the results, highlighting both the strengths and weaknesses of the algorithm under challenging conditions. The results should offer insights into the algorithm’s ability to handle complexity and scale, informing its potential for real-world applications.
Gradient Adjustment#
Gradient adjustment methods in multi-agent reinforcement learning aim to align individual and collective objectives by modifying the gradient updates of agents. These methods address the challenge of mixed-motive games, where individual incentives may conflict with overall group goals. Differentiable games provide a framework for analyzing these dynamics, allowing for the mathematical study of gradient adjustments. Existing approaches, like consensus gradient adjustment and symplectic gradient adjustment, show some success but often have limitations, particularly in handling complex scenarios or ensuring convergence to optimal solutions. A promising direction is using gradient adjustments to strategically guide the learning process towards stable fixed points of the collective objective while considering individual agent interests. Theoretical analysis can provide guarantees on convergence and stability, which is important for robust and reliable algorithms. Effective gradient adjustment techniques require careful design of the adjustment term and consideration of the underlying game dynamics. Future research should explore more sophisticated methods that can better handle high-dimensional spaces and complex interactions, ultimately leading to more robust and efficient multi-agent learning algorithms.
Future works#
The paper’s success in aligning individual and collective objectives using the AgA algorithm opens several exciting avenues for future research. Extending AgA to handle more complex scenarios such as those with incomplete information or dynamically changing environments is crucial. The algorithm’s current theoretical grounding focuses on fixed points; investigating its convergence properties in more general game settings is needed. The Selfish-MMM2 environment, while innovative, represents a single game. Future work should involve testing AgA across a wider range of mixed-motive games with varying complexities and scales to demonstrate its generalizability and robustness. Furthermore, exploring the impact of different gradient adjustment strategies and parameter tuning on AgA’s performance will enhance its practical applicability. Finally, investigating AgA’s performance in real-world applications is critical to assess its true potential and address any unforeseen challenges in complex, real-world multi-agent systems.
More visual insights#
More on figures

This figure shows the optimization trajectories of different algorithms in a two-player differentiable mixed-motive game. Subfigure (a) displays the trajectories on the collective reward landscape, highlighting that only Simul-Co and AgA successfully reach the social optimum. Subfigures (b) and (c) show the trajectories on the individual reward contours for Player 1 and Player 2, respectively. These subfigures demonstrate that Simul-Co prioritizes collective reward and neglects Player 1’s individual interests, while AgA successfully balances both individual and collective objectives.

This figure shows the optimization trajectories for different algorithms in a two-player differentiable mixed-motive game. The trajectories are shown in three different views: a 3D plot of the collective reward landscape, and 2D contour plots of the individual rewards for players 1 and 2. The figure highlights that the proposed AgA algorithm successfully aligns individual and collective objectives, unlike other methods, by optimizing along the summit of Player 1’s reward while maximizing the collective reward.
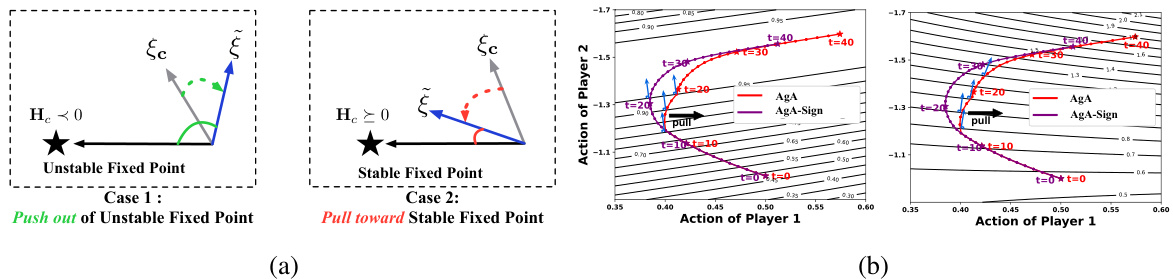
This figure shows the optimization trajectories for different algorithms in a two-player differentiable mixed-motive game. Panel (a) displays trajectories on a collective reward landscape, showing that only Simul-Co and AgA successfully reach the social optimum. Panels (b) and (c) show trajectories on individual reward contours, highlighting that Simul-Co prioritizes the collective objective at the expense of individual player interests, whereas AgA effectively balances both.
This figure shows the optimization trajectories of different algorithms in a two-player differentiable mixed-motive game. Panel (a) shows the trajectories in the collective reward landscape, highlighting that only Simul-Co and AgA successfully reach the social optimum. Panels (b) and (c) show the trajectories in the individual reward landscapes for players 1 and 2 respectively, demonstrating that AgA successfully aligns individual and collective objectives, while Simul-Co prioritizes collective rewards at the expense of player 1’s rewards.

This figure shows the results of a two-player public goods game experiment comparing several multi-agent reinforcement learning methods, including the proposed Altruistic Gradient Adjustment (AgA) method. Each point represents the actions taken by two players in a single game instance, with the color of the point indicating the method used. The ‘X’ marks show the average actions for each method. The figure highlights that most baselines converge to the Nash equilibrium (0,0), where neither player contributes. However, both AgA and Simul-Co show a tendency toward altruistic behavior (1,1), where both players contribute; AgA’s actions are more consistently clustered around the optimal outcome. This illustrates AgA’s superior alignment toward the socially optimal point.

This figure shows a simplified schematic of the Selfish-MMM2 environment used in the paper. It depicts the layout of the map in the StarCraft II game. It highlights the division of units between the controlled agents (teammates) and the enemy units. The controlled team consists of 1 Medivac, 2 Marauders, and 7 Marines. The opposing enemy team consists of 1 Medivac, 3 Marauders, and 8 Marines. This diagram visually represents the asymmetrical setup of the environment used to test the proposed algorithm.
More on tables

This table presents the average equality metric (E) for the Harvest and Cleanup environments. The equality metric, calculated using the Gini coefficient, measures the fairness of reward distribution among agents. Higher values indicate greater equality. The table compares the performance of AgA with different lambda values (λ = 0.1, 1, 100, 1000) against several baseline methods (Simul-Ind, Simul-Co, SVO, CGA, and SL). The results are averaged over three random runs, with mean and standard deviation reported. This table shows how AgA improves the equality of rewards compared to the baselines.

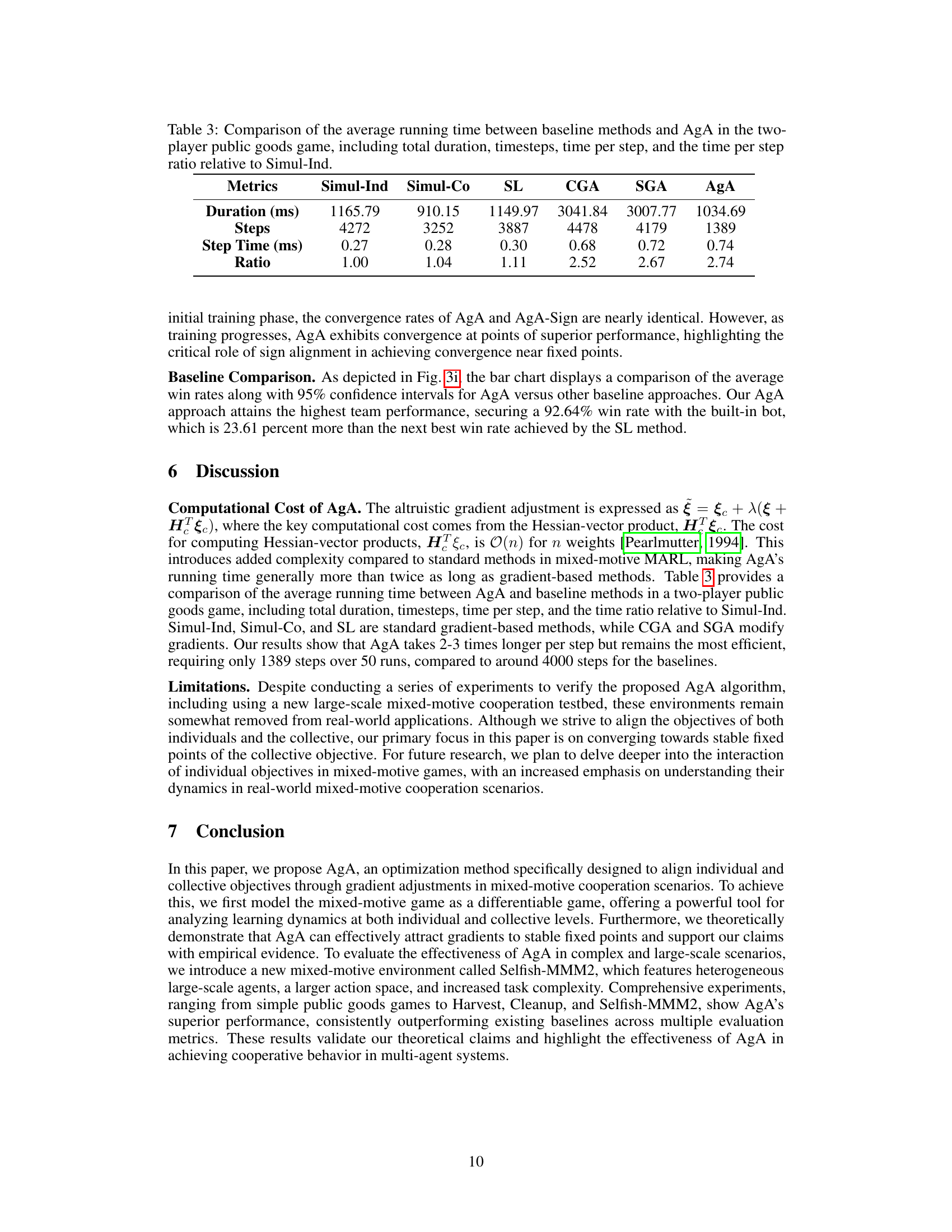
This table compares the computational efficiency of the AgA algorithm against several baseline methods in a two-player public goods game. It shows the total running time (Duration), the number of steps taken to converge (Steps), the average time per step (Step Time), and the ratio of the Step Time for each method relative to the Simul-Ind method. The table helps to demonstrate the trade-off between AgA’s improved performance and its slightly increased computational cost.
Full paper#