Optimal Scalarizations for Sublinear Hypervolume Regret

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working on multi-objective optimization, as it provides novel theoretical guarantees and empirical evidence for the effectiveness of hypervolume scalarization, a simple yet powerful technique for tackling complex optimization problems. It also introduces a novel algorithm for multi-objective stochastic linear bandits, which is optimal in a variety of scenarios. This opens new avenues for designing better multi-objective algorithms with strong theoretical foundations.

Visual Insights

#

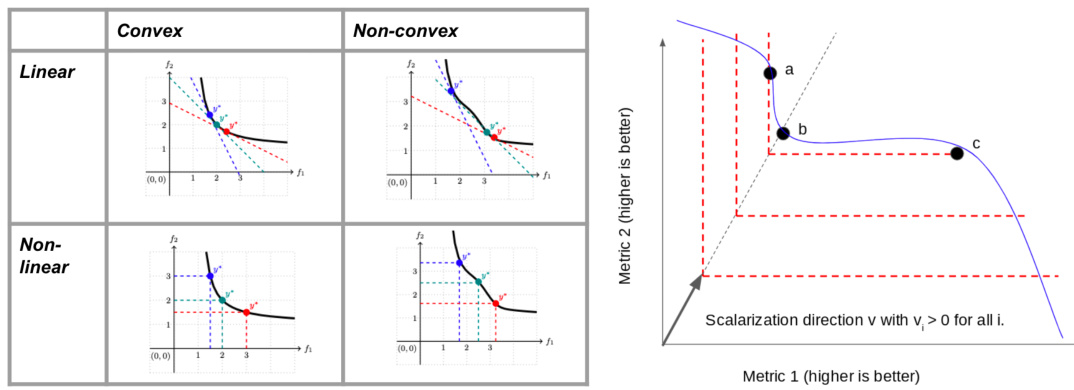
The figure compares linear and nonlinear scalarization methods for convex and non-convex Pareto fronts. Linear scalarization fails to find optima in concave regions, while nonlinear scalarization, with sharper level curves, discovers the entire Pareto front. The right panel illustrates how hypervolume scalarization targets specific parts of the Pareto frontier.

In-depth insights

#

Hypervolume Regret

#

Hypervolume regret, a crucial concept in multi-objective optimization, quantifies the difference between the hypervolume of the true Pareto front and that achieved by an algorithm after a certain number of evaluations. Minimizing hypervolume regret is a primary goal, as it directly measures the algorithm’s ability to effectively explore and approximate the optimal Pareto set. The paper explores theoretical bounds on hypervolume regret, demonstrating that a simple strategy using hypervolume scalarizations with randomly sampled weights achieves optimal sublinear regret. This optimality is significant, as it proves that a straightforward approach can match the performance of more complex adaptive algorithms. This result showcases the power of a well-designed scalarization technique, paving the way for designing simple yet effective multi-objective optimization strategies with provable performance guarantees. Furthermore, the analysis extends to the challenging setting of multi-objective linear bandits, showing that the hypervolume scalarization, with its specific properties, offers significant theoretical advantages.

Scalarization Methods

#

Scalarization methods are crucial for tackling multi-objective optimization problems by transforming multiple conflicting objectives into a single scalar objective. Linear scalarization, a common approach, uses weighted sums of objectives, but its limitation is its inability to explore non-convex Pareto frontiers. Non-linear scalarizations, like the Chebyshev scalarization and the novel Hypervolume scalarization presented, address this shortcoming by employing more complex functions. The choice of scalarization significantly impacts the exploration of the Pareto frontier; Hypervolume scalarization is shown to provide optimal sublinear hypervolume regret bounds, indicating its efficiency in discovering diverse optimal solutions. The selection of appropriate scalarization methods and weight distributions is therefore crucial for effective multi-objective optimization, especially when dealing with complex, non-convex problem landscapes. Adaptive weight strategies are also mentioned, suggesting that dynamically adjusting weights during optimization can further enhance the exploration and exploitation of the Pareto frontier.

Linear Bandits

#

In the context of multi-objective optimization, the exploration of linear bandits presents a unique challenge. Unlike single-objective scenarios where a simple reward function guides the optimization, linear bandits must balance the exploration of multiple objectives simultaneously. This exploration-exploitation trade-off becomes particularly complex when dealing with non-convex Pareto frontiers, as traditional linear scalarizations struggle to find solutions in concave regions. The paper addresses this challenge by introducing and analyzing non-linear scalarizations, specifically hypervolume scalarizations. These scalarizations, while more computationally intensive, prove to be theoretically optimal for minimizing hypervolume regret, which is the volume of the dominated portion of the Pareto frontier. Their effectiveness stems from sharp level curves that allow for targeted exploration of diverse Pareto points, even with an oblivious uniform weight distribution. Empirically, the paper demonstrates that these non-linear scalarizations significantly outperform linear counterparts and adaptive weighting strategies, especially in settings with high-dimensional objective spaces and non-uniform curvature. The analysis extends beyond synthetic examples to encompass natural settings, including multi-objective linear bandit problems and Bayesian optimization benchmarks, showcasing the broad applicability of the proposed techniques.

Empirical Analysis

#

An Empirical Analysis section of a research paper would ideally present a robust evaluation of the proposed methods. This would involve a detailed description of the datasets used, emphasizing their characteristics and relevance to the problem. The choice of evaluation metrics should be justified, highlighting their suitability for assessing the specific aspects of the problem. A strong empirical analysis would go beyond simply reporting results; it would present a clear methodology that explains the experimental setup, including details of data preprocessing, parameter tuning, and any relevant baseline comparisons. Furthermore, visualizations of results, such as graphs and tables, are crucial for enhancing clarity and facilitating understanding. The results interpretation should discuss not only the performance achieved but also any unexpected or surprising findings, and carefully address any limitations of the experimental setup or analysis. In short, a thorough empirical analysis must convincingly demonstrate the effectiveness and generalizability of the proposed approach, making the research credible and impactful.

Future Work

#

The “Future Work” section of this research paper could explore several promising avenues. Extending the theoretical analysis to more complex multi-objective optimization scenarios, such as those involving non-linear objectives or constraints, would significantly strengthen the paper’s contribution. Empirically evaluating the proposed hypervolume scalarization on a wider range of real-world problems, beyond the synthetic and benchmark datasets used in the current study, is crucial to demonstrate its practical applicability and robustness. Investigating the impact of different weight distributions and scalarization functions on the algorithm’s performance, and potentially developing adaptive weighting schemes, could offer significant performance improvements. Finally, a detailed comparison with other state-of-the-art multi-objective optimization algorithms across various problem classes is necessary to establish the method’s competitive edge. Addressing these points would solidify the paper’s findings and broaden its impact within the AI research community.

More visual insights

#

More on figures

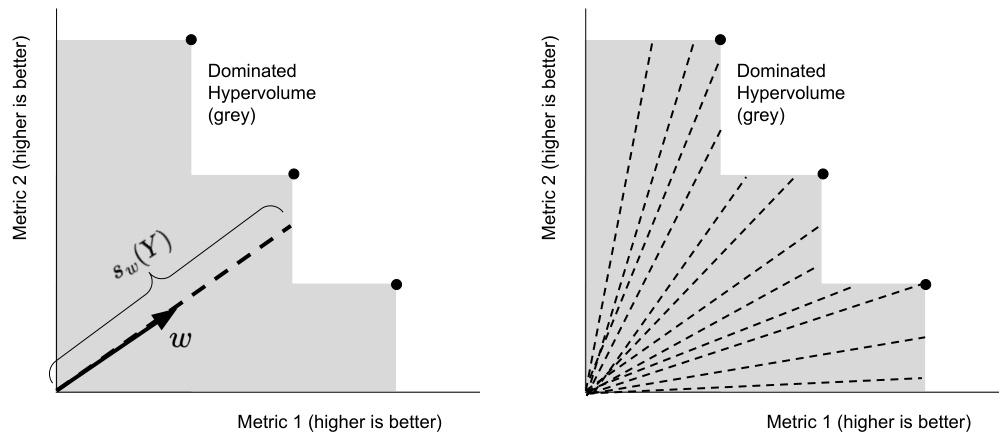
The figure shows how the hypervolume scalarization, with respect to a direction λ=w, corresponds to a differential area element in the dominated hypervolume. Averaging over random directions is analogous to integrating the dominated hypervolume in polar coordinates. This concept is used to prove that by choosing the maximizers of T random hypervolume scalarizations, the algorithm converges to the hypervolume of the Pareto frontier with a rate of O(T−1/k).

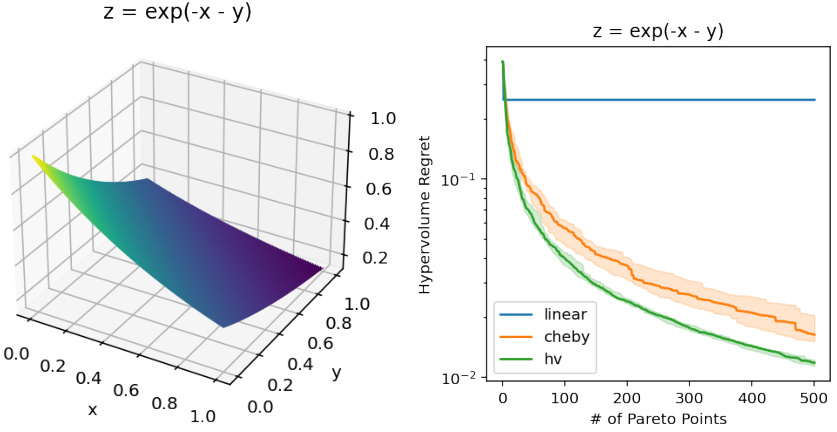
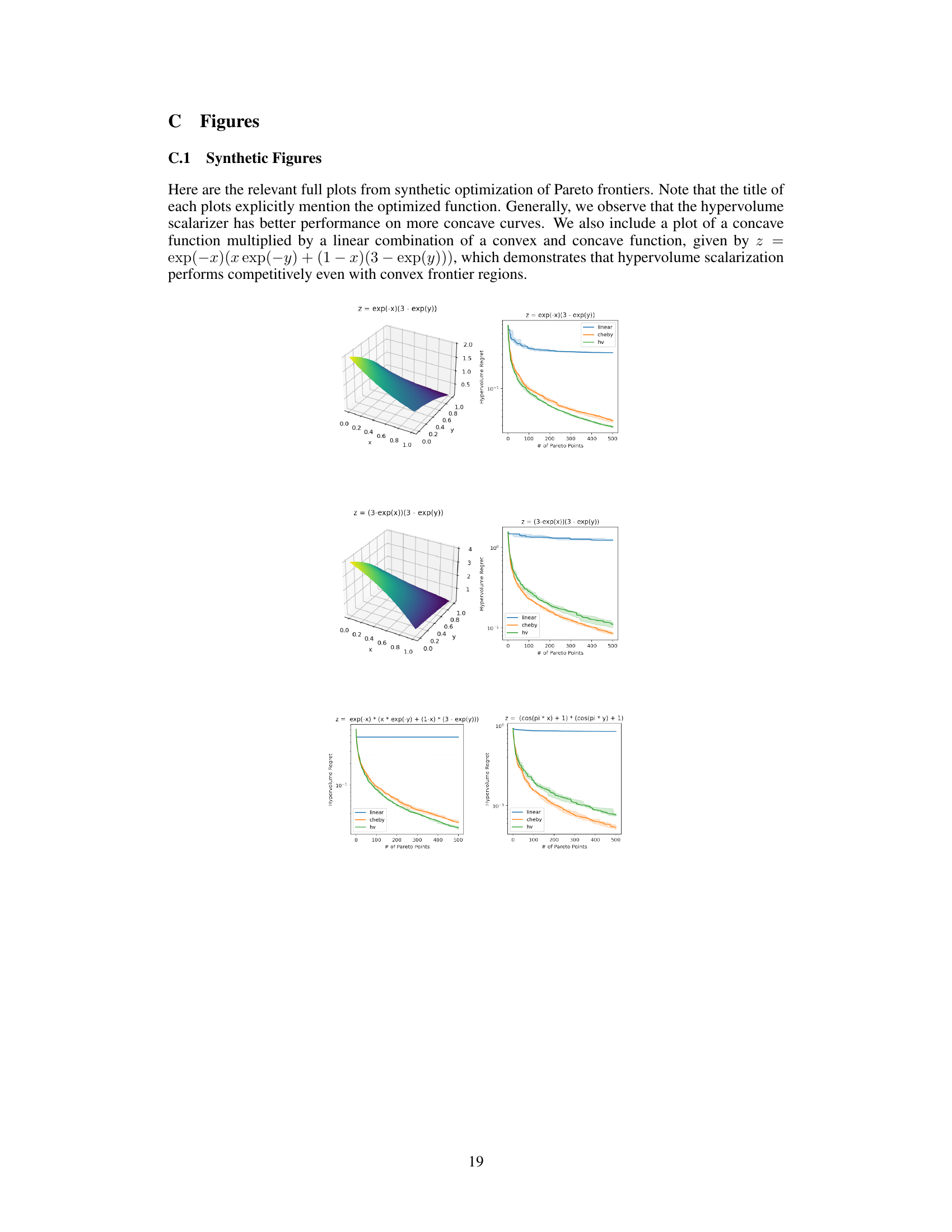
This figure compares the performance of three different scalarization methods (linear, Chebyshev, and hypervolume) on a synthetic concave Pareto frontier (z = exp(-x - y)). The left panel shows a 3D plot of the Pareto frontier. The right panel shows the hypervolume regret (the difference between the optimal hypervolume and the hypervolume achieved by the algorithm) as a function of the number of Pareto points selected. The results demonstrate that the hypervolume scalarization converges to the optimal hypervolume much faster than the other two methods. The linear scalarization’s regret remains constant, indicating it fails to effectively explore the Pareto frontier.

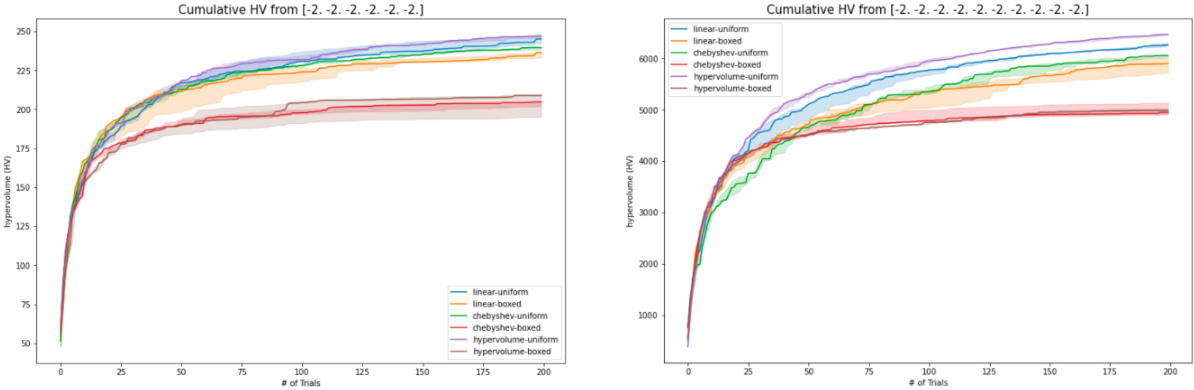
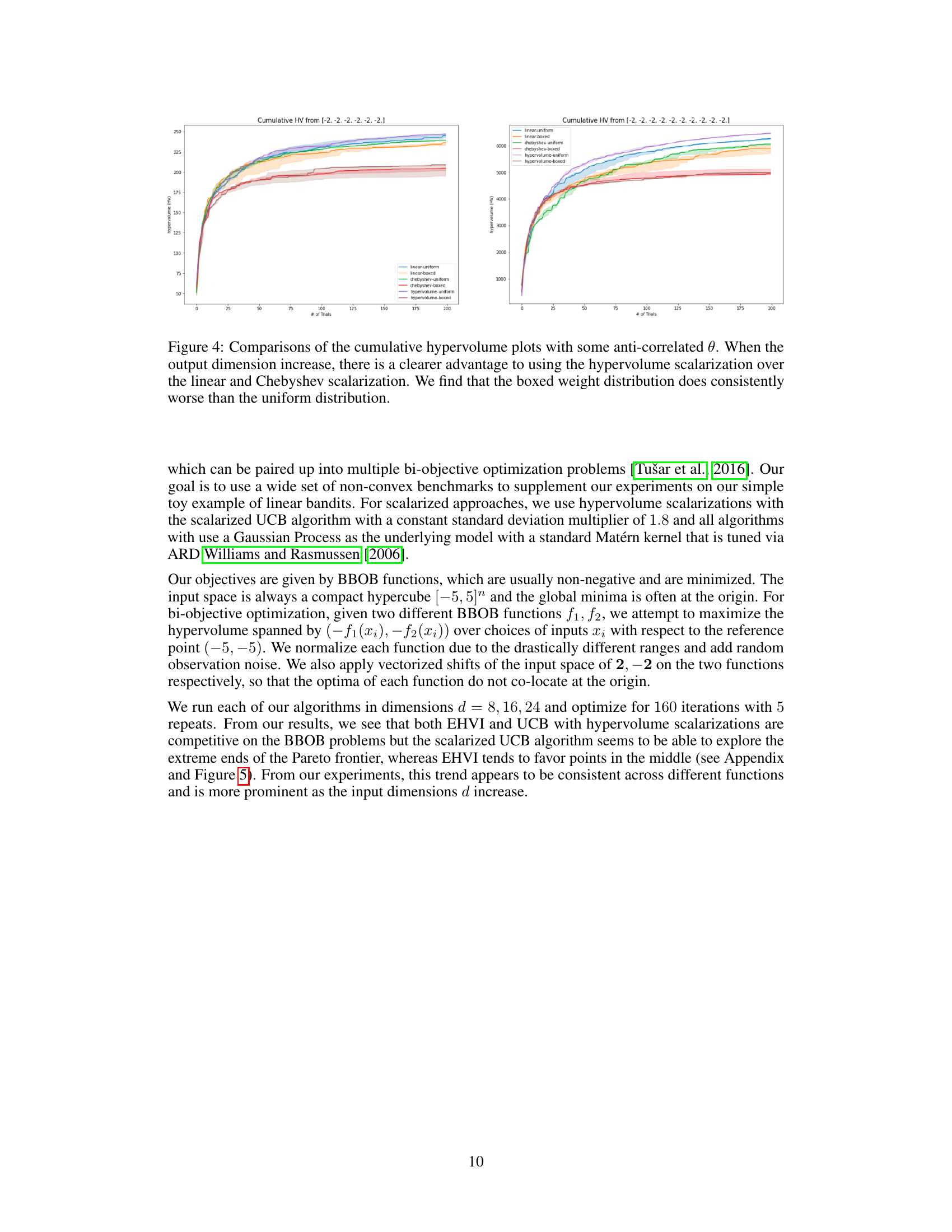
The plots compare the cumulative hypervolume achieved by different scalarization methods (linear, Chebyshev, hypervolume) with uniform and boxed weight distributions across various numbers of objectives (k=2,6,10). As the number of objectives increases, the hypervolume scalarization demonstrates a significantly better performance, indicating its superiority in exploring the Pareto frontier in higher-dimensional multi-objective optimization problems. The boxed weight distributions generally underperform compared to uniform distributions, highlighting the importance of uniform weight sampling in this context.

The figure compares the performance of three different scalarization methods (linear, Chebyshev, and hypervolume) in optimizing a synthetic concave Pareto frontier (z = exp(-x - y)). The hypervolume regret is plotted against the number of Pareto points selected. The results show that the hypervolume scalarization achieves a significantly faster convergence rate (sublinear) compared to the other methods, which demonstrate slower or constant convergence.

This figure compares the hypervolume regret of three different scalarization methods (linear, Chebyshev, and hypervolume) on a synthetic concave Pareto frontier (z = exp(-x - y)). The plot shows how the hypervolume regret (the difference between the maximum achievable hypervolume and the hypervolume achieved by the algorithm) changes as the number of Pareto points selected increases. The results demonstrate that the hypervolume scalarization converges significantly faster than the other two methods, achieving sublinear regret. The linear scalarization shows a constant hypervolume regret, suggesting it fails to efficiently explore the Pareto frontier.

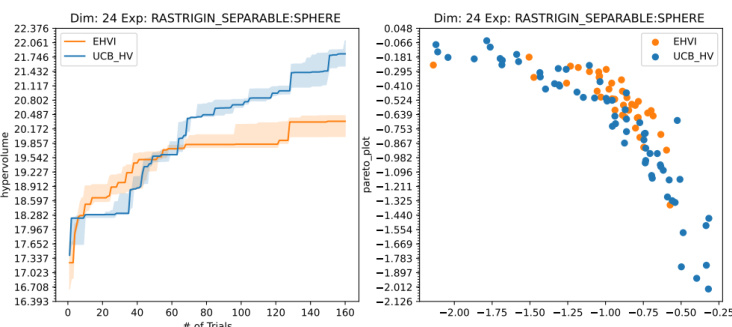
This figure compares the performance of two multi-objective optimization algorithms, UCB-HV and EHVI, on the BBOB benchmark functions. The left panel shows the dominated hypervolume over trials, and the right panel shows the Pareto frontier. UCB-HV, utilizing hypervolume scalarizations, demonstrates a more diverse exploration of the Pareto frontier compared to EHVI, particularly in higher dimensions, leading to greater hypervolume gains.

This figure compares the performance of UCB with hypervolume scalarization and EHVI algorithms on BBOB benchmark functions. The left panel shows the cumulative hypervolume achieved over a number of trials, highlighting the faster convergence rate of the UCB-HV method. The right panel visualizes the Pareto frontier obtained by both algorithms, revealing that EHVI tends to focus on the central part of the frontier while UCB-HV explores more diverse points, especially in higher dimensions. This supports the paper’s claim of superior performance of hypervolume scalarization in maximizing the diversity and hypervolume of Pareto front.

This figure compares the performance of the UCB algorithm with hypervolume scalarization and the EHVI algorithm on the BBOB benchmark for multi-objective optimization. The left panel shows the dominated hypervolume over time, indicating the efficiency of each method at exploring the Pareto frontier. The right panel displays the Pareto frontier approximation produced by each method, illustrating their differences in the diversity and distribution of solutions.

Full paper

#