↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Graph Neural Networks (GNNs) usually operate within a single geometric paradigm (Euclidean or hyperbolic). However, real-world graphs often exhibit geometrically heterogeneous characteristics, making it challenging to capture their intricate structural complexities using a single geometry. Existing methods often compute graph hyperbolicity and determine the best fit for the whole graph, ignoring local geometric properties.
This paper proposes a cross-geometric knowledge distillation framework that leverages both Euclidean and hyperbolic geometries in a space-mixing fashion. It employs multiple teacher models encoding graphs in different geometric spaces, generates hint embeddings to encapsulate distinct geometric properties, uses a structured knowledge transfer module, and incorporates geometric optimization to enhance training efficacy. The results show significantly improved performance in node classification and link prediction compared to traditional methods and establish the superiority of using multiple geometric contexts for GNN learning.
Key Takeaways#
Why does it matter?#
This paper is crucial because it bridges the gap between Euclidean and non-Euclidean graph neural networks (GNNs), offering a more adaptable approach for real-world graph data analysis. It introduces a novel framework with significant performance improvements, paving the way for advancements in various applications and prompting further research in geometry-aware GNNs.
Visual Insights#

This figure shows a comparison of graph embeddings in hyperbolic and Euclidean spaces. The left side illustrates how a graph is embedded in hyperbolic space, preserving tree-like structures and maximizing the distance between different classes. The right shows the embedding in Euclidean space, where some intra-class nodes are closer together, leading to potential classification issues. This visual demonstrates the strengths and weaknesses of each geometric space for representing graph data.
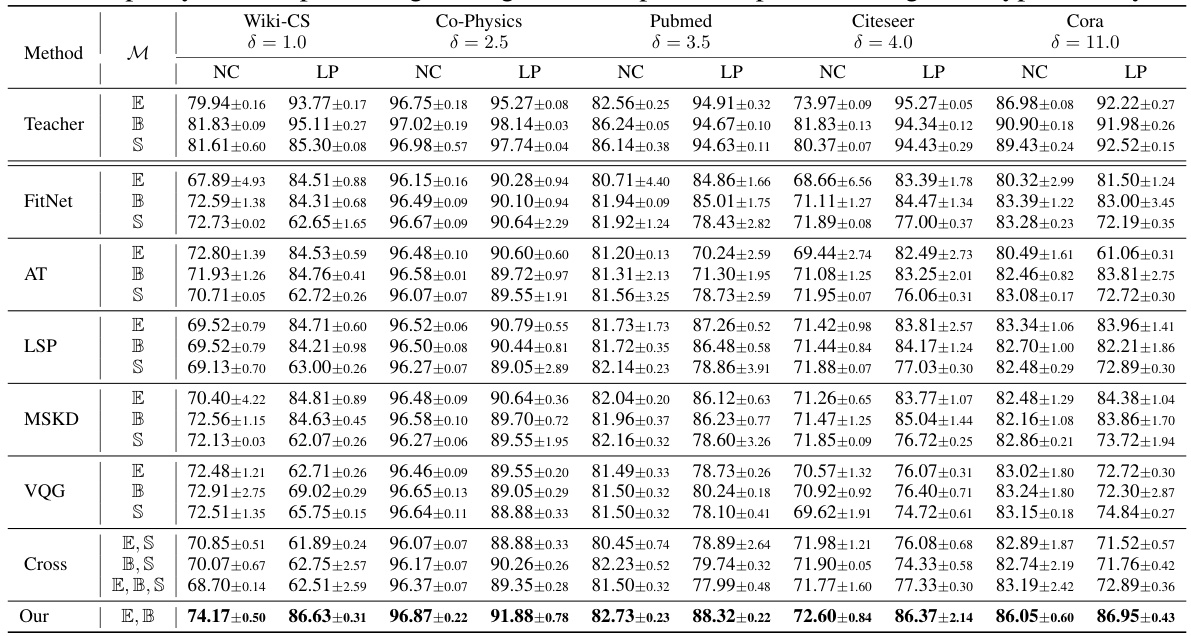
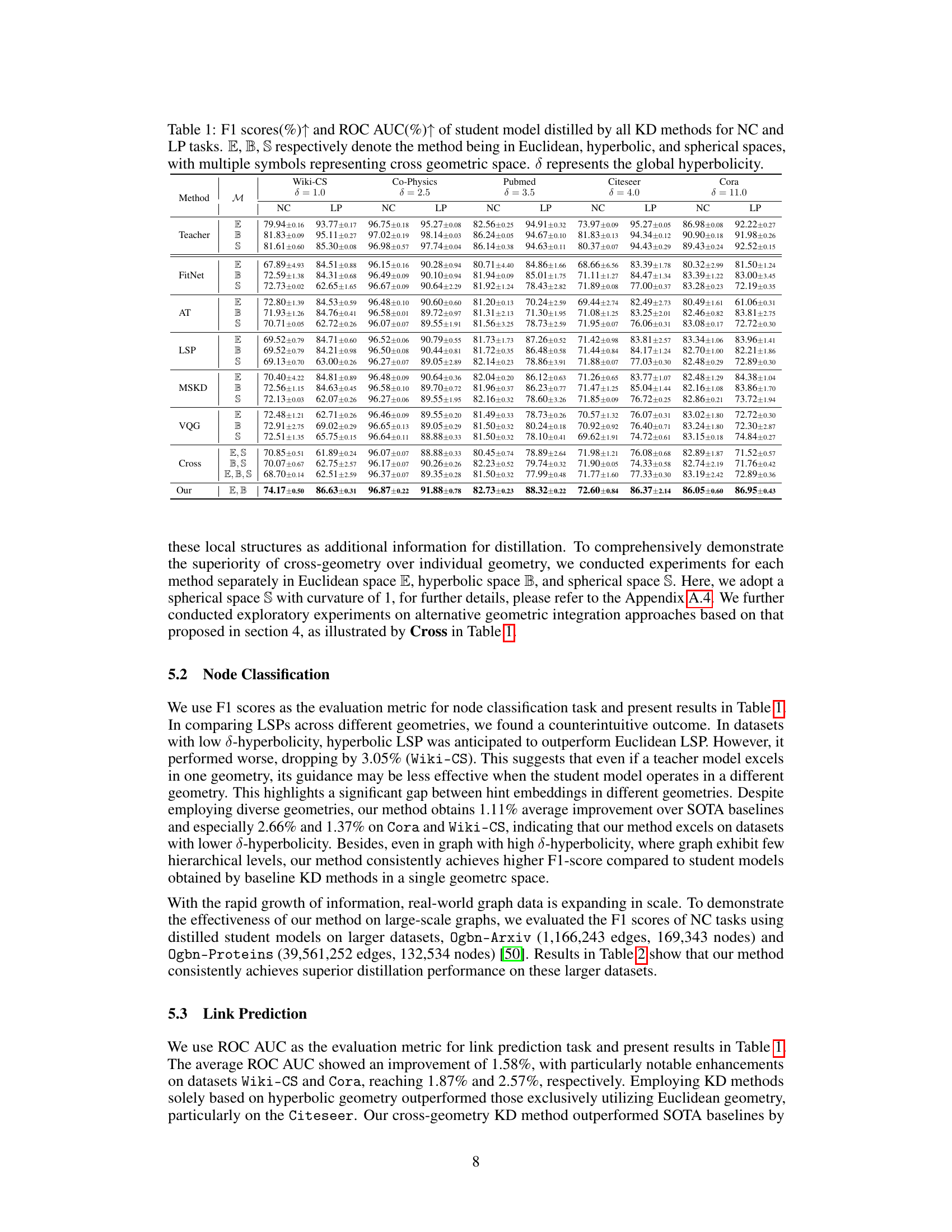
This table presents the F1 scores and ROC AUC for node classification (NC) and link prediction (LP) tasks. Different knowledge distillation (KD) methods are compared across Euclidean (E), hyperbolic (B), and spherical (S) geometries, both individually and in combinations. The results are shown for various datasets with different levels of hyperbolicity (δ). Higher scores indicate better performance.
In-depth insights#
Cross-Geom KD#
Cross-Geom KD, a novel knowledge distillation framework, tackles the challenge of geometric heterogeneity in real-world graph data by integrating both Euclidean and hyperbolic geometries. Unlike traditional methods confined to a single geometric paradigm, this approach leverages the strengths of each geometry to capture intricate structural complexities. Multiple teacher models, each specialized in a specific geometry, provide diverse hint embeddings. A structure-wise knowledge transfer module intelligently selects and utilizes these embeddings within their respective geometric contexts, boosting student model training. A crucial component, the geometric optimization network, bridges the distributional gaps between these embeddings, enhancing the overall performance and generalization of the student model. Experimental results demonstrate its superiority over traditional KD methods, particularly in node classification and link prediction tasks, showcasing its effectiveness in extracting and transferring topological graph knowledge. The framework’s model-agnostic nature makes it highly versatile and applicable to various GNN architectures.
Local Subgraph Geom#
The concept of “Local Subgraph Geom” suggests a novel approach to graph neural network (GNN) design, focusing on the local geometric properties of subgraphs within a larger graph. Instead of assuming a global geometric structure (Euclidean or hyperbolic), this method acknowledges the heterogeneity of real-world graphs. Each node’s neighborhood is analyzed individually to determine its optimal geometric representation. This adaptive geometry selection, based on local subgraph characteristics, allows the model to capture complex, nuanced relationships more effectively than a single-geometry approach. Knowledge distillation (KD) is likely a core component, leveraging multiple teacher models trained with different geometries to guide the learning process for a student model. The framework likely involves a mechanism for seamlessly integrating these diverse geometric perspectives, bridging potential distributional discrepancies between embeddings to create a unified, robust representation that enhances the student model’s performance on tasks such as node classification and link prediction. Computational efficiency is a key consideration due to the node-wise geometric analysis.
SWKT & GEO modules#
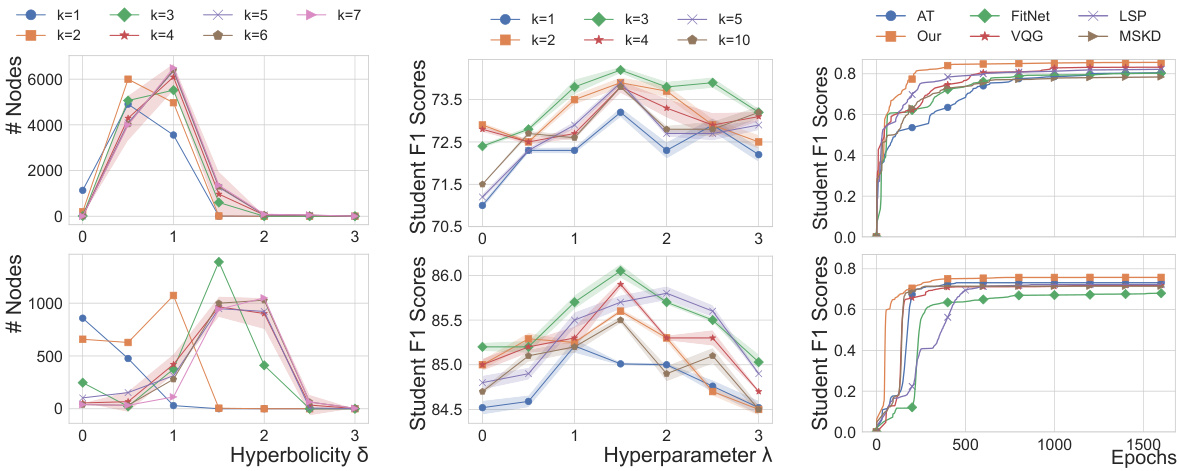
The paper introduces two novel modules, SWKT and GEO, to enhance knowledge distillation in graph neural networks. SWKT (Structure-Wise Knowledge Transfer) cleverly selects the optimal geometric space (Euclidean or hyperbolic) for each node’s local subgraph, maximizing the transfer of relevant knowledge to the student model. This is achieved by analyzing the local graph structure’s hyperbolicity. GEO (Geometric Embedding Optimization) addresses the potential inconsistencies arising from using multiple teacher models with different geometries. It refines hint embeddings by aligning their distributions across various geometric spaces, improving the student model’s ability to integrate information effectively. The combination of SWKT and GEO allows for a more robust and accurate knowledge transfer, achieving superior performance compared to traditional KD methods. The framework’s model-agnostic design makes it broadly applicable to diverse GNN architectures. The approach demonstrates a deeper understanding of leveraging geometrical properties for improved model training, particularly in handling complex, heterogeneous graph data.
Geom. Heterogeneity#
Geometric heterogeneity in graph data presents a significant challenge for traditional Graph Neural Networks (GNNs). Real-world graphs rarely conform to a single, uniform geometric structure, exhibiting diverse characteristics across different regions. Some areas might exhibit tree-like structures best suited to hyperbolic geometry, while others display dense, clustered patterns more effectively modeled using Euclidean space. A framework ignoring this heterogeneity limits the expressive power of GNNs because it forces a single geometric representation to capture diverse topological characteristics. Therefore, effective GNN models must adapt to the varying geometric properties inherent within a single graph. This adaptation may involve using multiple geometric representations simultaneously, or dynamically switching between suitable geometries based on local context. A cross-geometric approach, combining Euclidean and non-Euclidean representations, is crucial to overcome this limitation. This allows the model to leverage the strengths of each geometry, leading to more accurate and robust graph representations and improved performance on downstream tasks.
Future Works#
Future research could explore several promising avenues. Extending the cross-geometric framework to encompass additional geometries, such as spherical or other non-Euclidean spaces, could further enhance performance and generalizability. Investigating more sophisticated knowledge distillation techniques, beyond simple hint embeddings, may improve knowledge transfer and robustness. This includes exploring different loss functions and transfer methods. Applying the model to a broader range of graph datasets and tasks will validate its effectiveness in diverse domains. Finally, a deeper analysis of the geometric embedding optimization module could lead to improved efficiency and optimization strategies. A more detailed investigation into selecting optimal hyperparameters, and potentially adapting them dynamically during training, warrants further study.
More visual insights#
More on figures
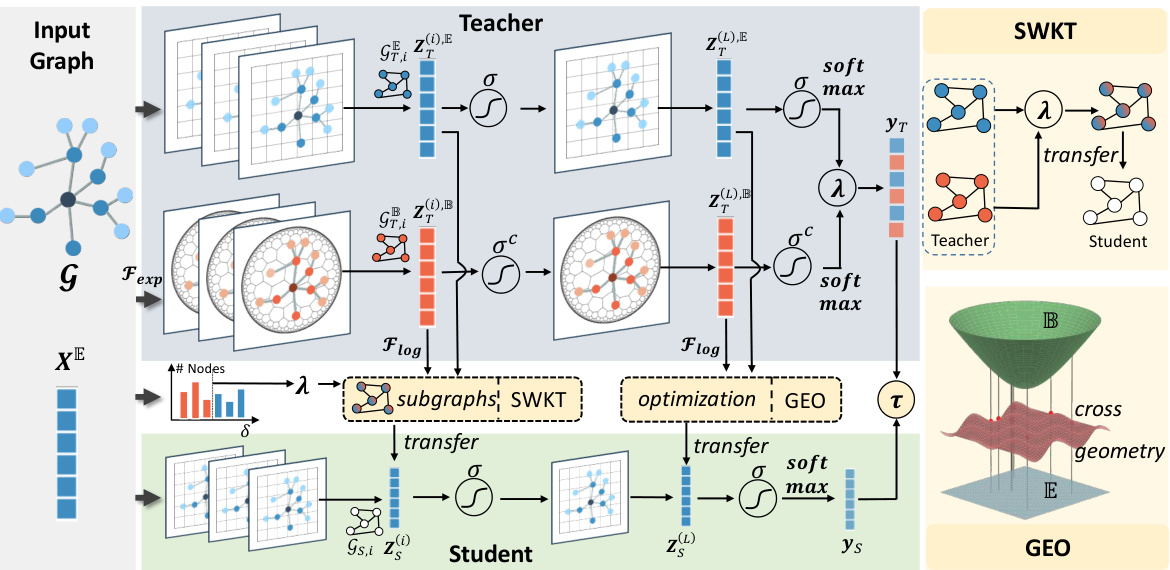
This figure illustrates the proposed cross-geometry graph knowledge distillation (KD) framework. It shows how multiple teacher models (using Euclidean and hyperbolic geometries) generate hint embeddings that encapsulate distinct geometric properties. A structure-wise knowledge transfer module leverages these embeddings to enhance student model training. A geometric optimization network bridges distributional disparities among embeddings. The framework uses local subgraph analysis to select the most appropriate geometry for each subgraph. This is visualized as selecting between Euclidean and hyperbolic embeddings.
This figure illustrates the proposed cross-geometry graph knowledge distillation (KD) framework. It highlights two key modules: Structure-Wise Knowledge Transfer (SWKT) and Geometric Embedding Optimization (GEO). SWKT selects the most appropriate geometric space (Euclidean or hyperbolic) for embedding each node based on its local subgraph’s hyperbolicity. GEO optimizes the distribution of hint embeddings from multiple teacher models to mitigate inconsistencies between different geometries, thereby improving knowledge transfer to the student model.

This figure visualizes four different types of spaces with varying curvatures: spherical (positive curvature), Euclidean (zero curvature), and two hyperbolic spaces with different negative curvatures. It illustrates how the curvature affects the geometry of the space, particularly the rate at which volume grows as one moves away from a central point. The image helps to understand the differences between these geometries in the context of graph representation, where different geometries might be more suitable for different types of graph structures.

This figure shows the t-SNE visualization of node embeddings generated by different knowledge distillation methods, including FitNet, AT, LSP, MSKD, VQG, and the proposed cross-geometry method. The visualization reveals that the proposed method produces embeddings that better utilize the embedding space, resulting in significantly larger inter-class distances compared to other methods. This improved separation of classes in the embedding space leads to better classification performance.

This figure illustrates the proposed cross-geometry graph knowledge distillation (KD) framework. It shows how the framework uses multiple teacher models (Euclidean and Hyperbolic) to generate hint embeddings which encapsulate distinct geometric properties. A Structure-Wise Knowledge Transfer (SWKT) module selects appropriate embeddings based on local subgraph analysis. A Geometric Optimization (GEO) module refines the embeddings to reduce inconsistencies between different geometric spaces. Finally, the refined embeddings are transferred to the student model for improved performance.
More on tables

This table presents the F1 scores achieved by different knowledge distillation (KD) methods on node classification (NC) tasks using the Arxiv and Proteins datasets. It compares the performance of the student models trained using various KD techniques across different geometric spaces, highlighting the effectiveness of the proposed cross-geometry KD method in achieving superior performance compared to traditional KD approaches using single geometric spaces.
This table presents the results of node classification (NC) and link prediction (LP) tasks using different knowledge distillation (KD) methods. It compares the performance of models trained using only Euclidean geometry (E), only hyperbolic geometry (B), only spherical geometry (S), and combinations of these geometries. The F1 score and ROC AUC are reported for each dataset and method, demonstrating the superiority of the cross-geometry approach. The global hyperbolicity (δ) of each dataset is also indicated.
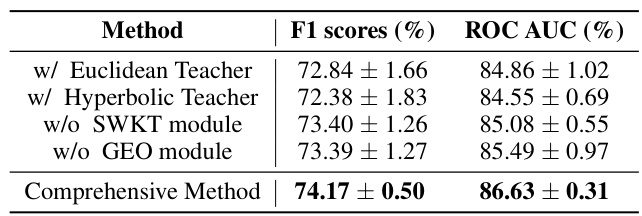
This table presents the results of an ablation study conducted to evaluate the impact of individual components of the proposed cross-geometry graph knowledge distillation framework. It shows the performance (F1 scores and ROC AUC) of the model when using only a Euclidean teacher, only a hyperbolic teacher, without the Structure-Wise Knowledge Transfer (SWKT) module, without the Geometric Embedding Optimization (GEO) module, and with the comprehensive method (including both SWKT and GEO). The results highlight the contribution of each component to the overall performance improvement.

This table presents the F1 scores and ROC AUC values achieved by various knowledge distillation (KD) methods on node classification (NC) and link prediction (LP) tasks. Different KD methods are compared, using either Euclidean (E), hyperbolic (B), or spherical (S) geometry, or combinations thereof. The results are shown for several datasets with varying levels of global hyperbolicity (δ), demonstrating the performance of different geometric approaches for graph data.

This table presents the performance comparison of various knowledge distillation (KD) methods on node classification (NC) and link prediction (LP) tasks across different datasets. It shows F1 scores and ROC AUC values for different KD methods using Euclidean, hyperbolic, and spherical geometries individually as well as combinations thereof. The global hyperbolicity (δ) of each dataset is also provided, offering context for interpreting the results. Higher F1 scores and ROC AUC indicate better performance.

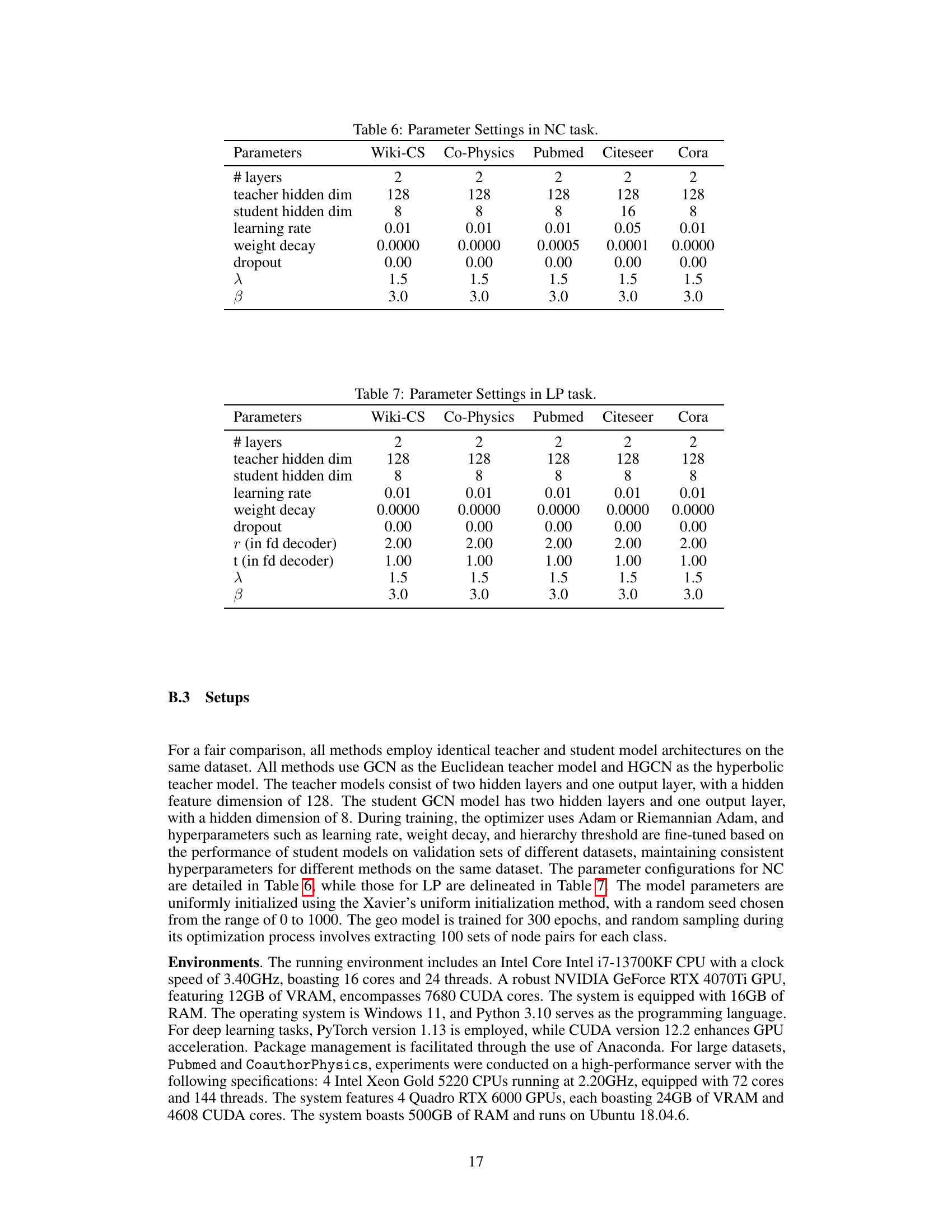
This table presents the hyperparameters used in the node classification (NC) task for each dataset. The hyperparameters include the number of layers in both the teacher and student models, the dimensions of the hidden layers, the learning rate, weight decay, dropout rate, and the lambda (λ) and beta (β) parameters used in the cross-geometry knowledge distillation framework. The values indicate the settings used to optimize the model’s performance on each dataset.

This table shows the hyperparameters used for the node classification (NC) task on five different datasets: Wiki-CS, Co-Physics, Pubmed, Citeseer, and Cora. The parameters include the number of layers in the model, the dimensions of the hidden layers for both the teacher and student models, the learning rate, weight decay, dropout rate, and the hyperparameters λ and β specific to the proposed cross-geometry knowledge distillation method.

This table presents the F1 scores achieved by student models trained using knowledge distillation (KD) with Graph Attention Networks (GATs) as teacher models. The results are broken down by dataset (Wiki-CS, Co-Physics, Pubmed, Citeseer, Cora), geometry used for the teacher models (Euclidean (E), Hyperbolic (B), Spherical (S), and combinations thereof), and the overall best performing cross-geometry method. Higher F1 scores indicate better performance.

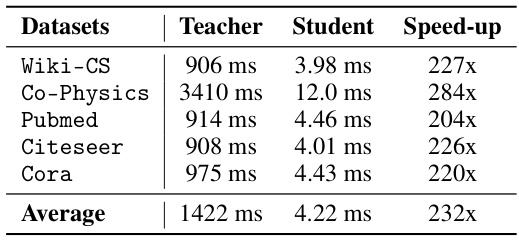
This table presents the F1 scores achieved by student models trained using knowledge distillation (KD) with Graph Transformer Network (GTN) teacher models. The results are broken down by the geometry used (Euclidean (E), Hyperbolic (B)) for both the teacher and student models, showing the performance improvement from cross-geometric training. Inference times are included for both the GTN and GCN student models to highlight the efficiency of the GCN student.

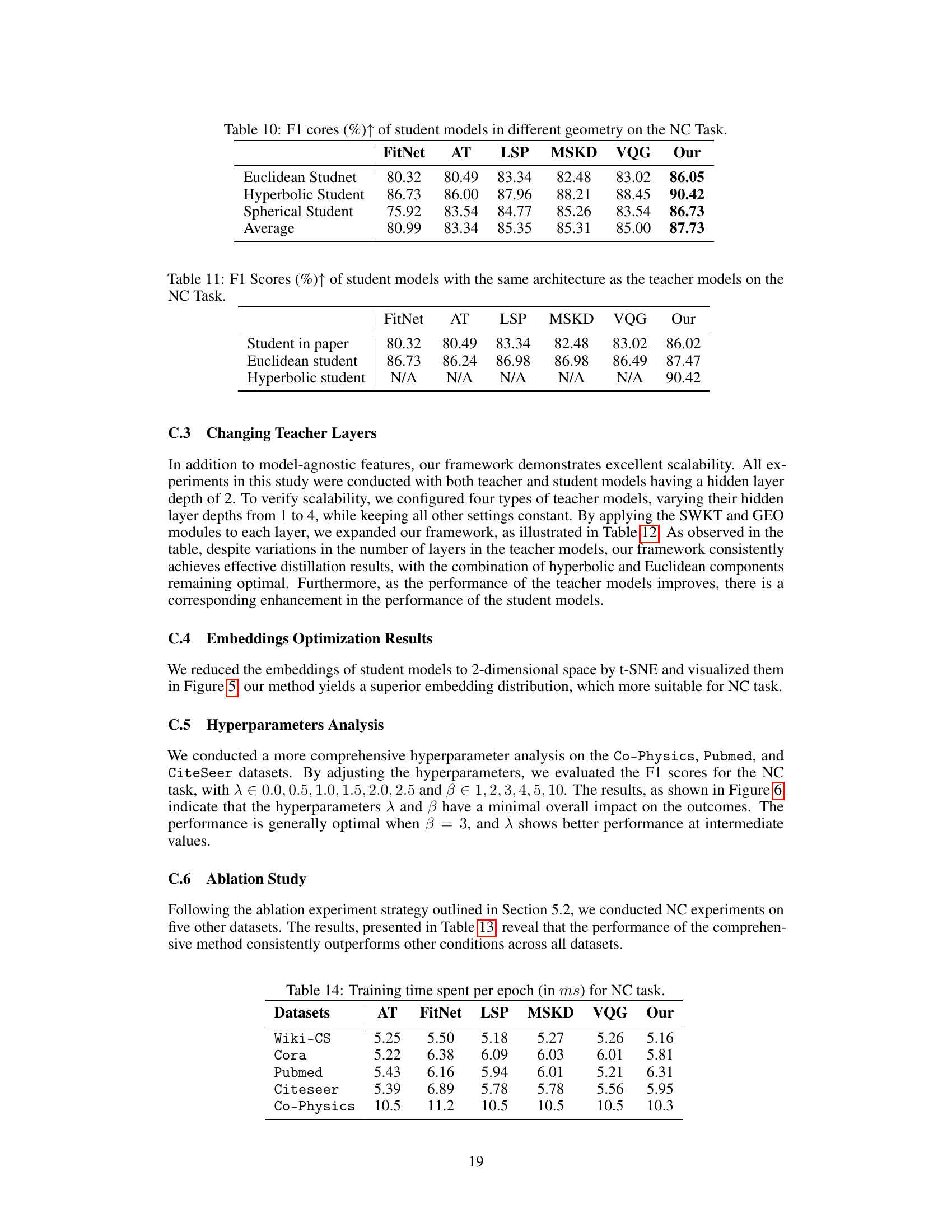
This table presents the F1 scores achieved by student models trained using different KD methods and geometric spaces (Euclidean, Hyperbolic, Spherical). The results showcase the performance of each method in each geometry, offering a comparison of their effectiveness in node classification tasks.

This table presents the F1 scores achieved by student models that have the same architecture as the teacher models for the node classification task. The results are compared across various knowledge distillation (KD) methods, including FitNet, AT, LSP, MSKD, VQG, and the proposed cross-geometry KD method. The table highlights the performance differences when using Euclidean and Hyperbolic student models and the improvement achieved by the proposed method compared to baseline techniques.
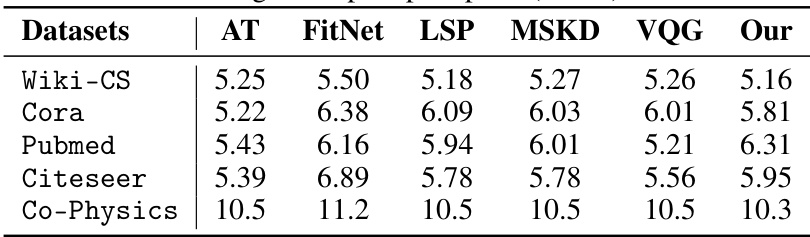
This table presents the performance of various Knowledge Distillation (KD) methods on node classification (NC) and link prediction (LP) tasks across different datasets. Each method is tested using Euclidean (E), hyperbolic (B), and spherical (S) geometries, as well as combinations thereof. The F1 score and ROC AUC are reported, along with the global hyperbolicity (d) of each dataset, providing a comprehensive comparison of the methods across different geometric settings.

This table presents the F1 scores achieved by student models trained using knowledge distillation from teacher models with varying numbers of layers (1, 2, 3, and 4). The results are shown for three different scenarios: using a single geometry (Euclidean, Hyperbolic, Spherical), combining two geometries, and combining all three geometries. The table highlights the performance of the proposed cross-geometry approach (‘Our’) against traditional single-geometry and combined-geometry knowledge distillation methods. The results demonstrate the robustness and scalability of the proposed method across different teacher model layer configurations.

This table presents the F1 scores and ROC AUC values achieved by various knowledge distillation (KD) methods on node classification (NC) and link prediction (LP) tasks. It compares the performance of models trained using Euclidean geometry (E), hyperbolic geometry (B), spherical geometry (S), and combinations thereof. The global hyperbolicity (δ) of each dataset is also provided, showing the effectiveness of different geometric approaches under varying dataset characteristics.
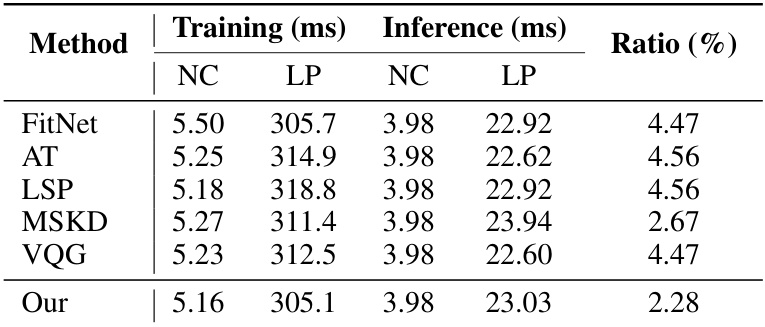
This table presents the performance comparison of different knowledge distillation (KD) methods on node classification (NC) and link prediction (LP) tasks using various graph datasets. The methods are categorized into Euclidean (E), hyperbolic (B), spherical (S) and cross-geometric approaches. The table shows F1 scores and ROC AUC scores, along with the global hyperbolicity (δ) for each dataset, indicating the effectiveness of each method across different geometric spaces and dataset characteristics.
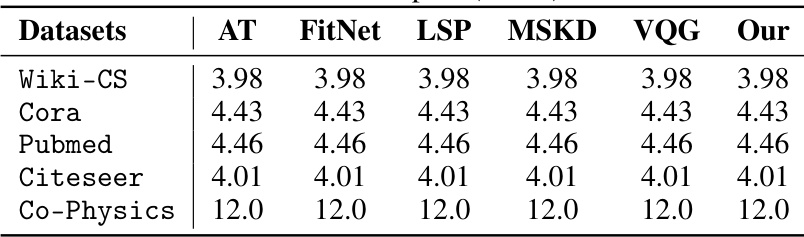
This table presents the performance comparison of various knowledge distillation (KD) methods on node classification (NC) and link prediction (LP) tasks. It shows F1 scores and ROC AUC values for different KD methods applied to datasets with varying global hyperbolicities. Each method is evaluated using Euclidean (E), hyperbolic (B), spherical (S) spaces, and combinations thereof, showcasing the impact of different geometric spaces on the performance of student models trained via KD.

This table presents the performance comparison of various knowledge distillation (KD) methods on node classification (NC) and link prediction (LP) tasks. It shows the F1 scores and ROC AUC values achieved by different KD methods across various graph datasets. The methods are categorized by the geometric space they use (Euclidean, Hyperbolic, Spherical, and combinations thereof). The global hyperbolicity (δ) of each dataset is also provided, offering context for performance variations across different geometries.
Full paper#