Global Rewards in Restless Multi-Armed Bandits

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working on resource allocation problems with non-separable rewards. It introduces a novel framework and adaptive algorithms, pushing the boundaries of existing restless multi-armed bandit models and opening new avenues for research in various real-world applications.

Visual Insights

#

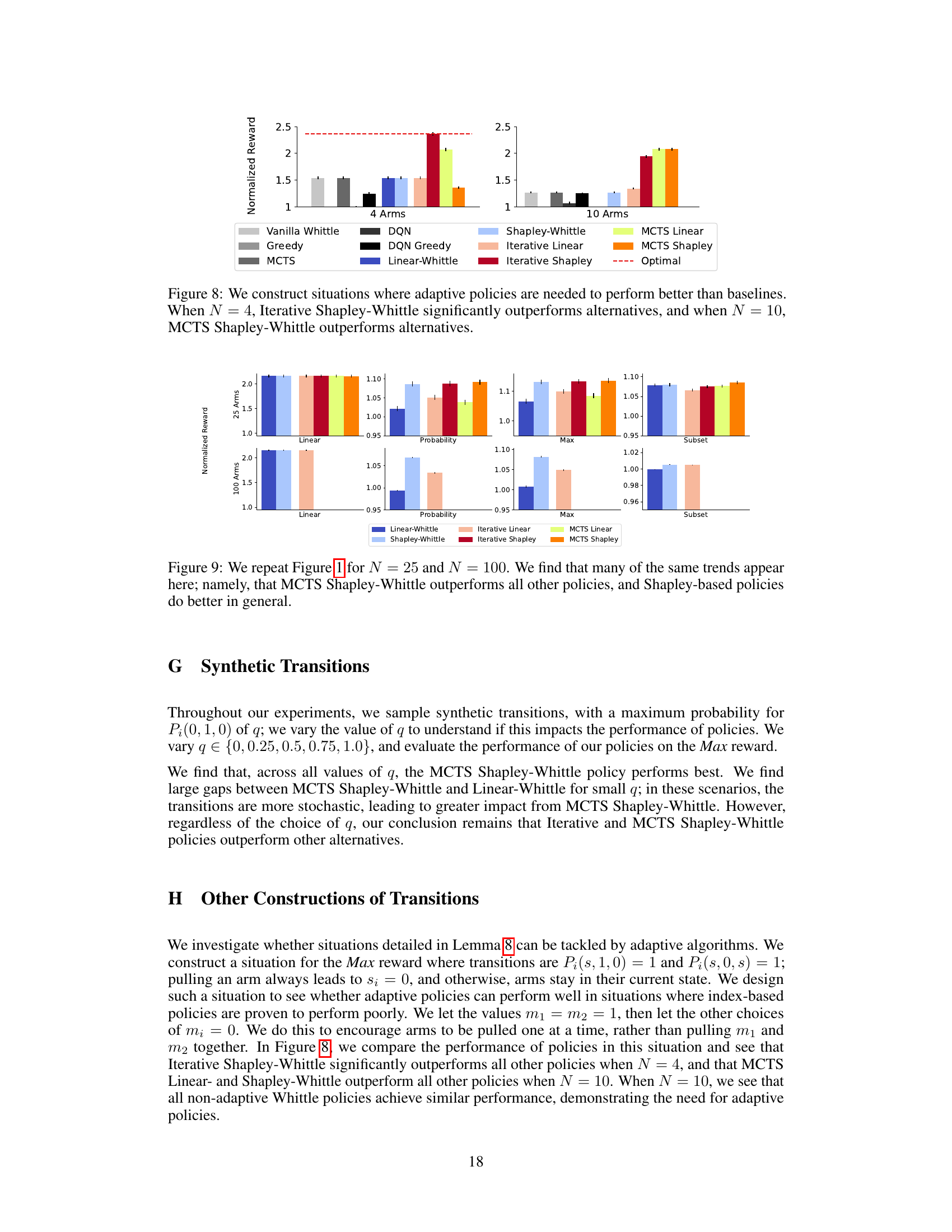
This figure compares the performance of different restless multi-armed bandit (RMAB) policies on synthetic data with four different reward functions (Linear, Probability, Max, Subset). It shows that the proposed adaptive policies (Iterative and MCTS Shapley-Whittle) consistently outperform baseline methods and are close to optimal for smaller problem sizes (N=4).

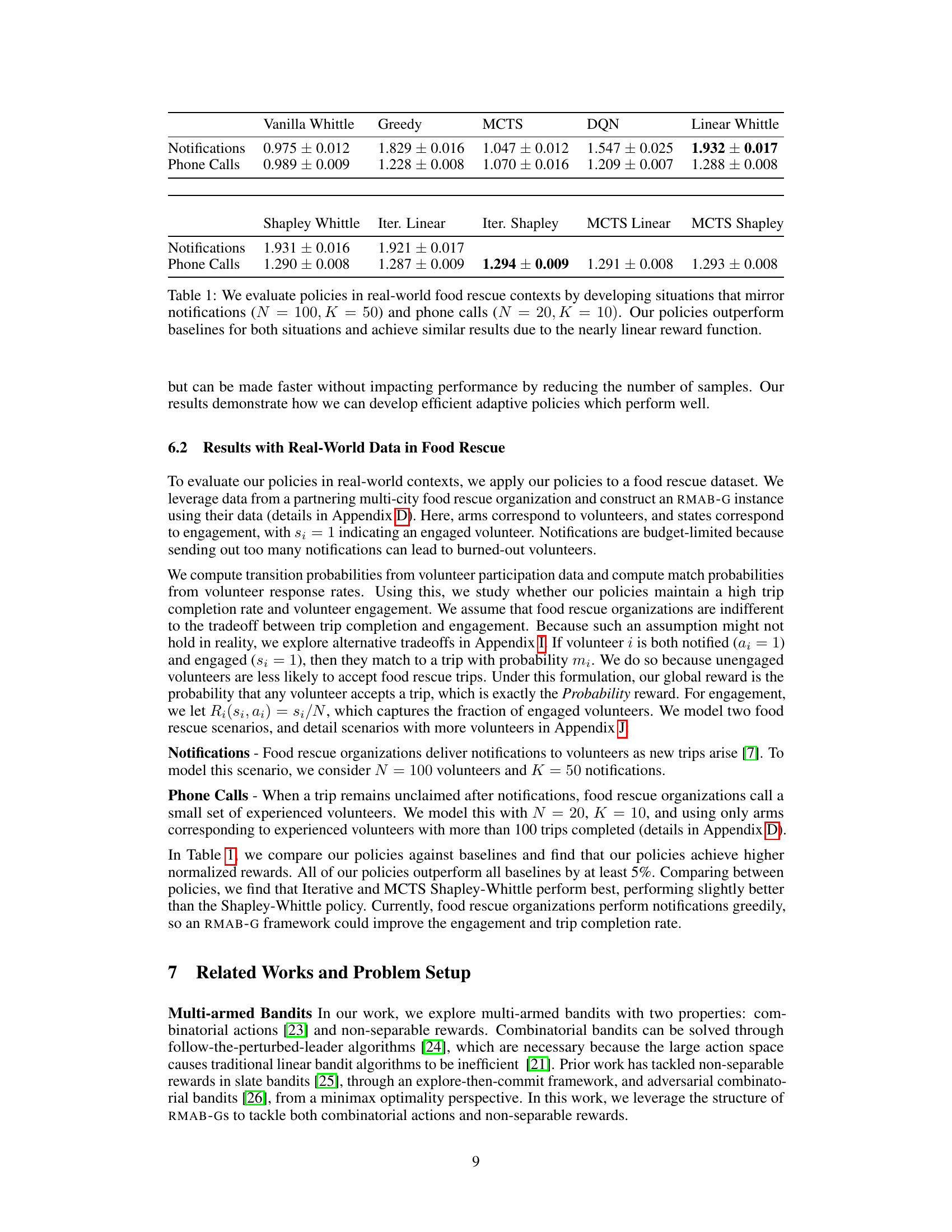
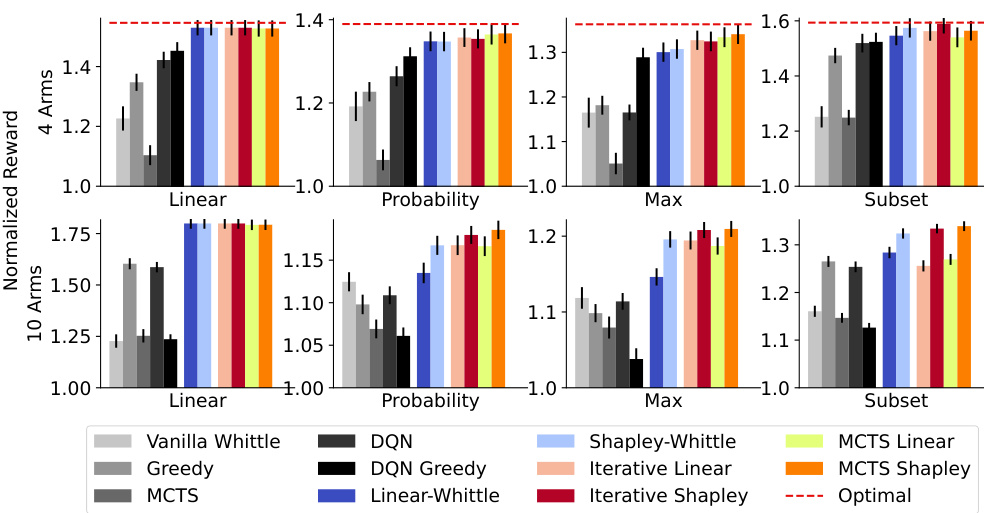
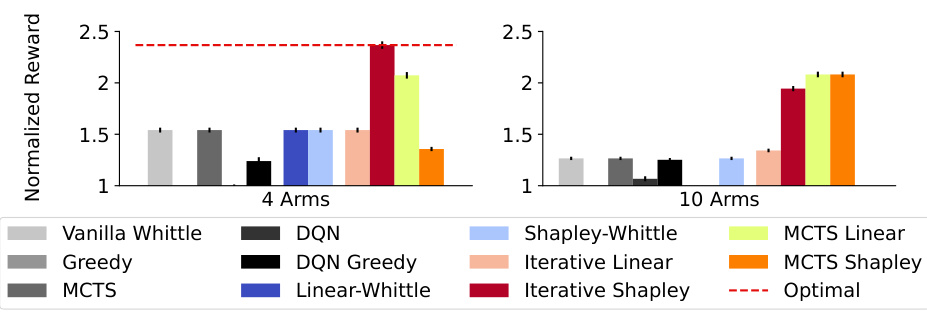
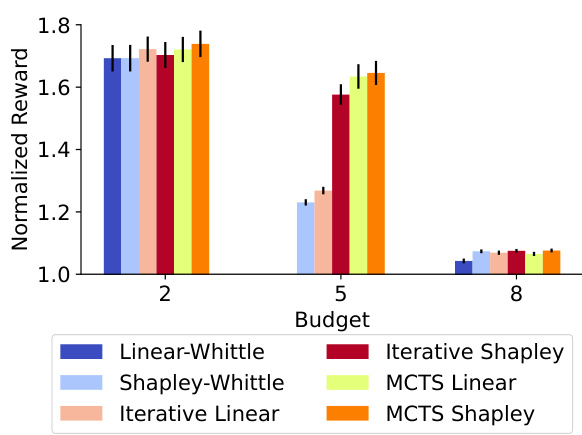
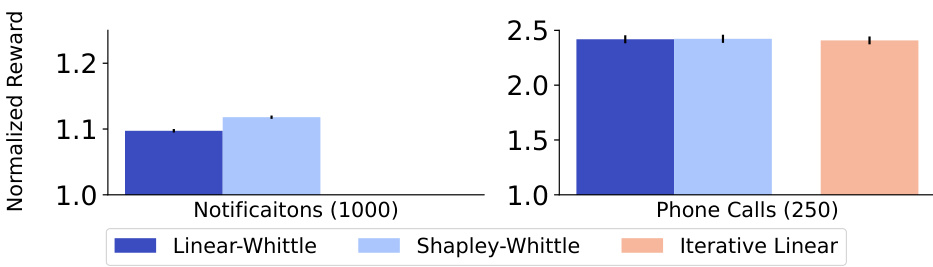
This table shows the performance comparison of different policies (Vanilla Whittle, Greedy, MCTS, DQN, Linear Whittle, Shapley Whittle, Iterative Linear, Iterative Shapley, MCTS Linear, and MCTS Shapley) on two real-world food rescue scenarios: notifications and phone calls. The results demonstrate the superior performance of the proposed adaptive policies compared to baselines in both scenarios. The near-linear nature of the reward function explains the relatively small difference in performance among the different policies.

In-depth insights

#

Global Reward RMAB

#

The concept of “Global Reward RMAB” introduces a significant extension to the standard Restless Multi-Armed Bandit (RMAB) framework. Traditional RMABs assume rewards are separable, meaning the overall reward is simply the sum of individual arm rewards. However, many real-world problems exhibit non-separable global rewards, where the overall reward depends on the complex interaction between the chosen arms. This is where “Global Reward RMAB” shines. It explicitly addresses this limitation by modeling scenarios where the reward function is a non-linear, possibly submodular, function of the selected arms. This formulation allows for a more realistic representation of problems like food rescue, where the successful completion of a rescue mission depends on the synergistic contributions of various volunteers, rather than on a simple sum of individual volunteer efforts. Consequently, this extension necessitates the development of new solution methods beyond standard Whittle indices, which are inherently designed for separable reward structures. Approaches such as Linear- and Shapley-Whittle indices, and more advanced adaptive policies involving iterative index computation or Monte Carlo Tree Search (MCTS) have been developed to address the challenges of optimization in this more complex setting. The power of “Global Reward RMAB” lies in its ability to capture the intricate dependencies between actions and significantly broaden the applicability of RMABs to a wider array of practical decision-making problems.

Index Policy Limits

#

The heading ‘Index Policy Limits’ suggests an examination of the shortcomings and constraints of index policies within the context of restless multi-armed bandits (RMABs) or a similar reinforcement learning framework. A thoughtful analysis would likely explore the theoretical limitations of index policies, such as their asymptotic optimality assumptions, their performance in non-separable reward settings, and their sensitivity to model misspecification. The discussion may delve into computational complexity, assessing whether the computation of indices scales well with problem size (number of arms, states, time horizon). It’s also likely that the analysis would touch upon the empirical performance of index policies, comparing them to alternative approaches in various scenarios and datasets, highlighting cases where indices fail to provide satisfactory solutions. Specific types of limitations that might be discussed include scenarios with highly non-linear reward functions, sparse reward settings, or those involving complex state transitions that violate the fundamental assumptions behind the index approach. Overall, this section would likely provide valuable insights into the applicability and robustness of index policies, guiding the selection of appropriate algorithms for specific RMAB problem instances.

Adaptive Policies

#

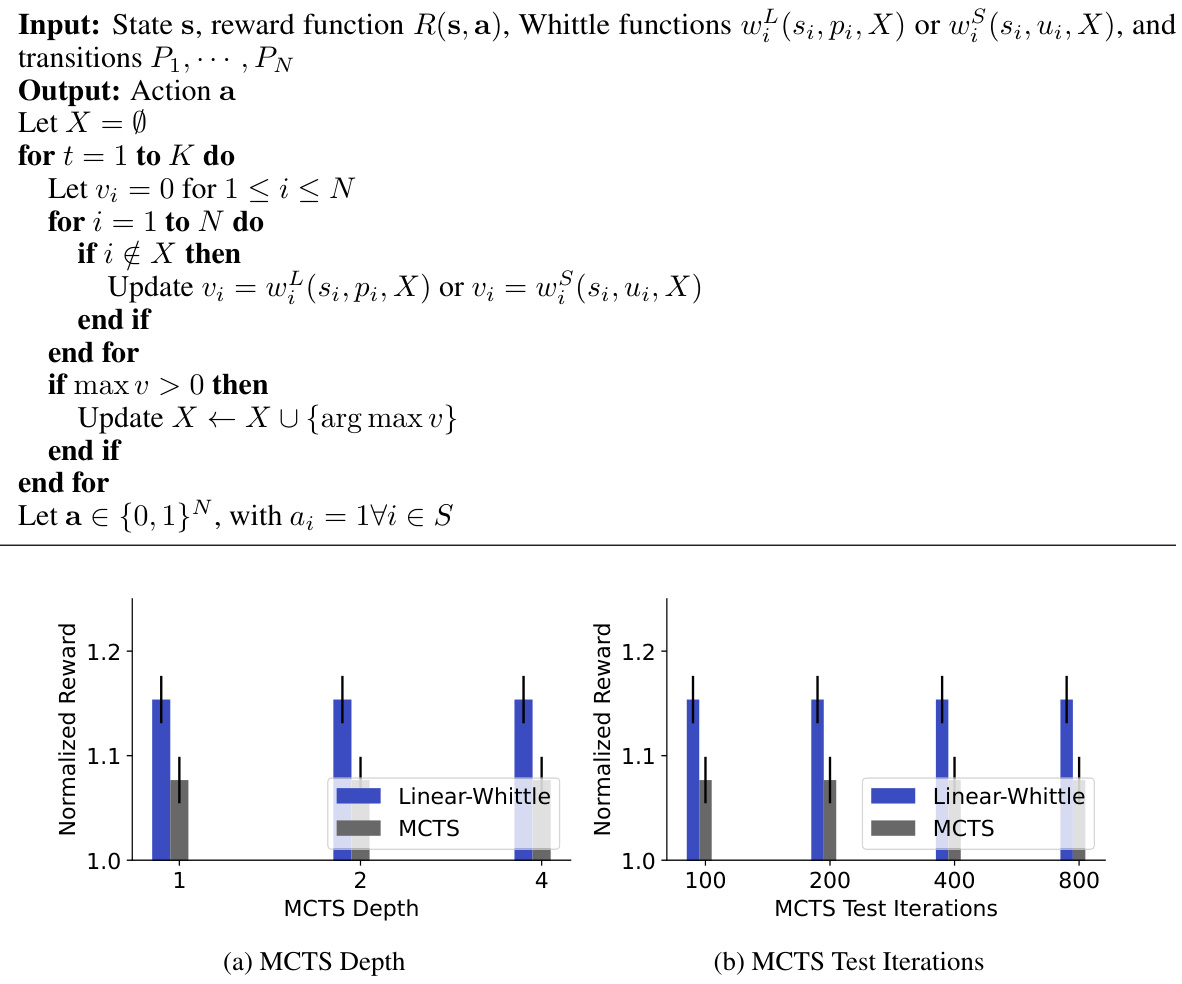
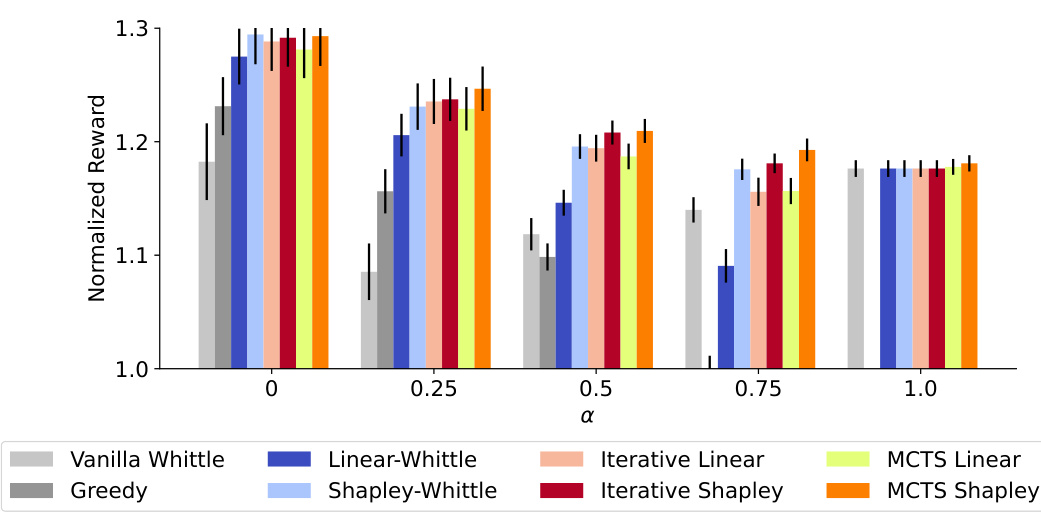
The core idea behind adaptive policies in restless multi-armed bandits with global rewards (RMAB-G) is to overcome the limitations of pre-computed index-based policies, which struggle with highly non-linear reward functions. These policies dynamically adjust their arm selection based on current rewards and observed states, unlike pre-computed methods that rely on static indices. Two main approaches are presented: iterative policies and Monte Carlo Tree Search (MCTS)-based policies. Iterative policies refine their index calculations at each time step, incorporating the immediate impact of arm selections on the global reward. This iterative refinement helps to address the non-separability of rewards, a crucial characteristic of the RMAB-G problem. MCTS-based policies enhance greedy selection by exploring various arm combinations, using the indices to estimate future rewards. The combination of iterative index updates and MCTS search allows for a more comprehensive exploration of the decision space, leading to superior performance, especially when rewards are highly non-linear. The empirical results demonstrate the superiority of these adaptive approaches over baselines and pre-computed methods across various reward functions and real-world scenarios, highlighting their practical relevance.

Food Rescue Use

#

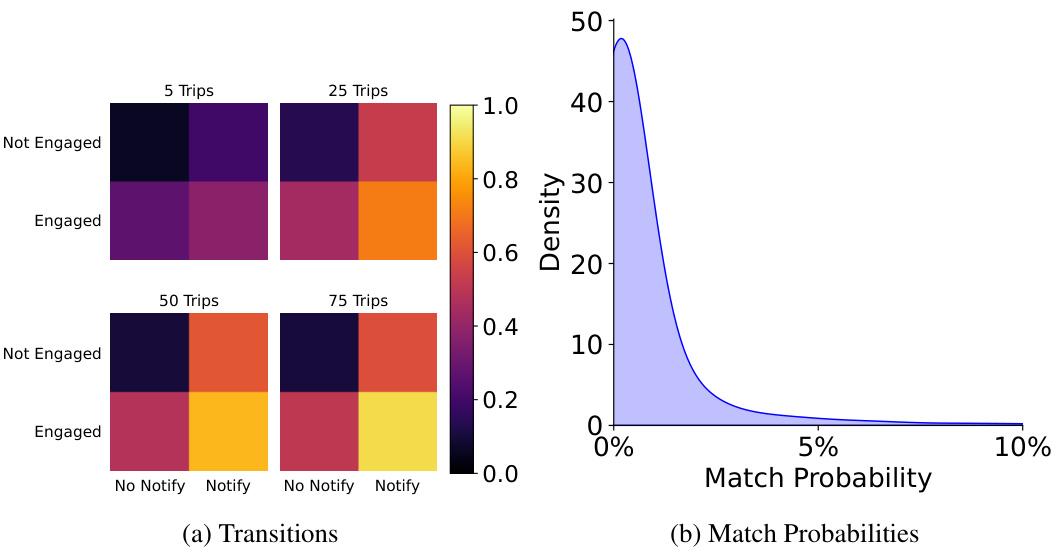
The application of restless multi-armed bandits (RMABs) to food rescue presents a compelling case study. Food rescue operations face the challenge of efficiently allocating limited resources (volunteers, transportation) to maximize the number of successful food pickups. The non-separable nature of the reward (successful trip completion) in this context, where a single volunteer’s participation may be sufficient, highlights the limitations of traditional RMAB models that assume separable rewards. The paper introduces restless multi-armed bandits with global rewards (RMAB-G) as a more suitable framework. This extension effectively addresses the complexities of non-separable rewards, paving the way for algorithms that can optimize food rescue efficiency. The empirical evaluation on real-world food rescue data is a crucial aspect, demonstrating the practical value of the proposed RMAB-G framework and its outperformance over baselines. The success of the adaptive policies, which explicitly address non-linear reward functions, underscores the significance of considering such policies for real-world optimization problems.** This research showcases not just an algorithmic advance but also a practical application of advanced resource allocation techniques to a pressing social issue.

Future Research

#

Future research directions stemming from this work on restless multi-armed bandits with global rewards (RMAB-G) could explore several promising avenues. Extending the theoretical analysis to encompass more complex reward functions beyond submodular and monotonic ones is crucial for broader applicability. The current approximation bounds provide valuable insights into index-based policies, but developing theoretical guarantees for the adaptive approaches (iterative and MCTS-based) remains a significant challenge. Empirical evaluation on a wider range of real-world datasets across diverse domains is needed to demonstrate the robustness and generalizability of the proposed algorithms. Furthermore, investigating the impact of different budget constraints and exploring alternative reward structures that better reflect specific application needs would offer valuable insights. Developing more efficient algorithms for scenarios with high dimensionality and complex state spaces is also critical. Finally, integrating the RMAB-G framework with other machine learning techniques like reinforcement learning could lead to hybrid approaches that leverage the strengths of both paradigms for enhanced decision-making in dynamic environments.

More visual insights

#

More on figures

This figure compares the performance of different policies (baselines and proposed policies) on four different reward functions with 4 and 10 arms. The results show that all the proposed policies outperform the baselines, and among them, Iterative and MCTS Shapley-Whittle policies perform the best and are close to optimal performance for the case of 4 arms.

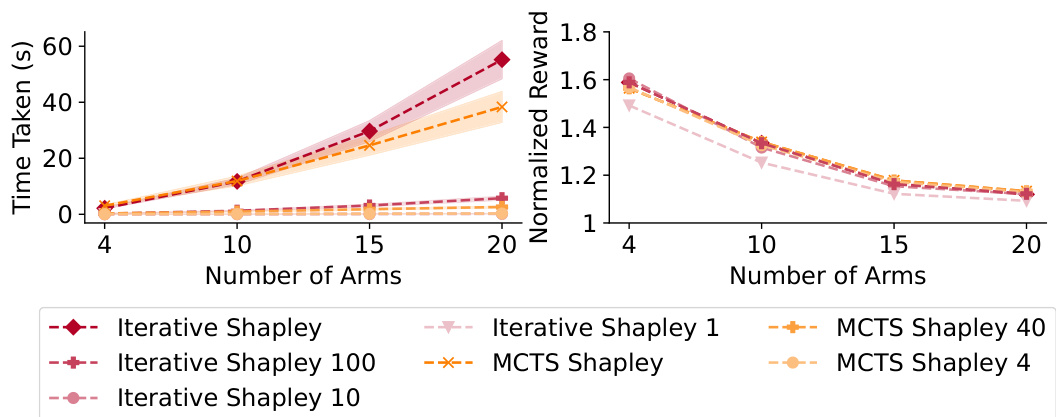
The figure compares the performance of six proposed policies (Linear-Whittle, Shapley-Whittle, Iterative Linear-Whittle, Iterative Shapley-Whittle, MCTS Linear-Whittle, and MCTS Shapley-Whittle) against several baseline methods (Random, Vanilla Whittle, Greedy, MCTS, DQN, and DQN Greedy) across four different reward functions (Linear, Probability, Max, and Subset) with 4 and 10 arms. The results show that all proposed policies outperform baselines, with Iterative and MCTS Shapley-Whittle consistently achieving the best performance, and coming within 3% of optimal for N=4.

This figure compares the performance of different restless multi-armed bandit (RMAB) policies on four different reward functions. The policies include baselines (Random, Vanilla Whittle, Greedy, MCTS, DQN, DQN Greedy), index-based policies (Linear-Whittle, Shapley-Whittle), and adaptive policies (Iterative Linear-Whittle, Iterative Shapley-Whittle, MCTS Linear-Whittle, MCTS Shapley-Whittle). The results show that all the proposed policies outperform the baselines, and the Iterative and MCTS Shapley-Whittle consistently achieve the best performance. The performance is within 3% of optimal for problems with 4 arms.

The figure compares the performance of several restless bandit algorithms across four reward functions. The algorithms include baselines (Random, Vanilla Whittle, Greedy, MCTS, DQN, DQN Greedy), index-based policies (Linear-Whittle, Shapley-Whittle), and adaptive policies (Iterative Linear, Iterative Shapley, MCTS Linear, MCTS Shapley). The results show that all proposed policies outperform the baselines. For smaller problem sizes (N=4), the best performing policy is within 3% of optimal. The Iterative and MCTS Shapley-Whittle policies consistently show the best performance across reward functions.

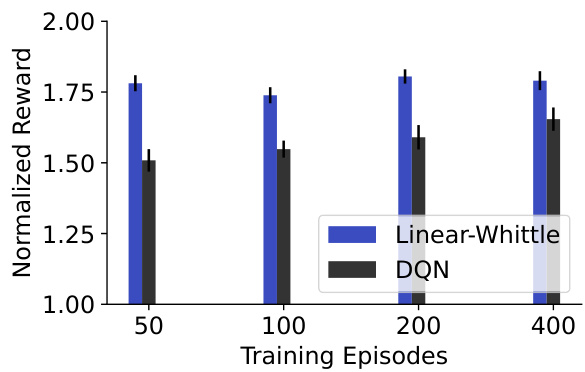
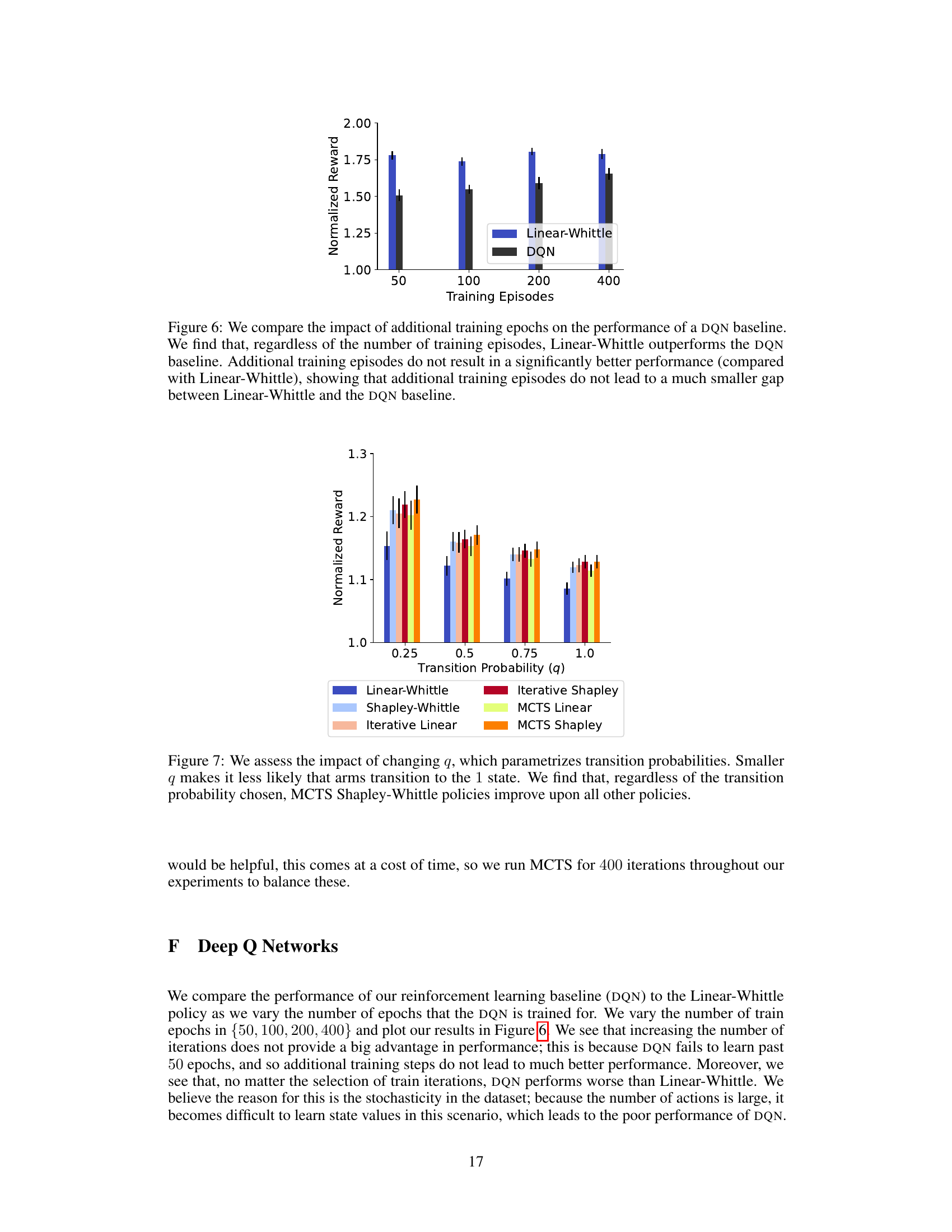
The figure shows the comparison of the performance of Linear-Whittle and DQN algorithms with varying training epochs (50, 100, 200, and 400). The results indicate that Linear-Whittle consistently outperforms DQN across all training epochs. Increasing training epochs does not significantly improve DQN’s performance, suggesting that additional training does not close the performance gap between Linear-Whittle and DQN.

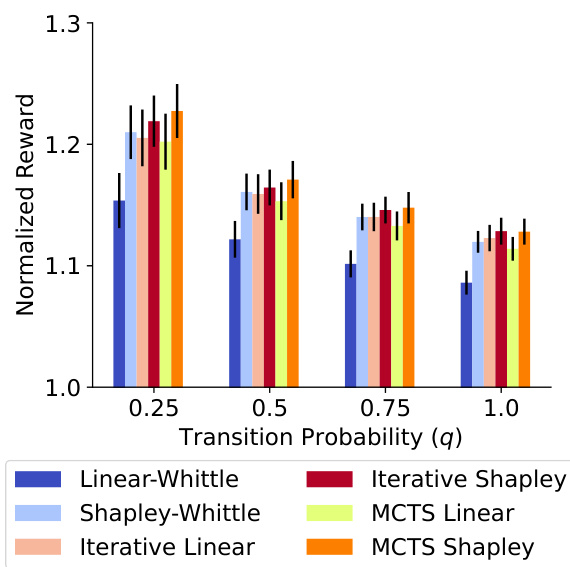
This figure shows the performance of different restless multi-armed bandit (RMAB) policies under varying transition probabilities (parameterized by q). Lower values of q indicate a lower probability of arms transitioning to state 1. The results demonstrate the consistent superior performance of the MCTS Shapley-Whittle policy across all transition probabilities.

This figure compares the performance of several policies (baselines and the proposed ones) on restless multi-armed bandits with global rewards for different reward functions. The results show that the proposed policies consistently outperform the baselines across various reward functions, with Iterative and MCTS Shapley-Whittle showing the best performance. For smaller problem sizes (N=4 arms), the best-performing policy achieves near-optimal results.

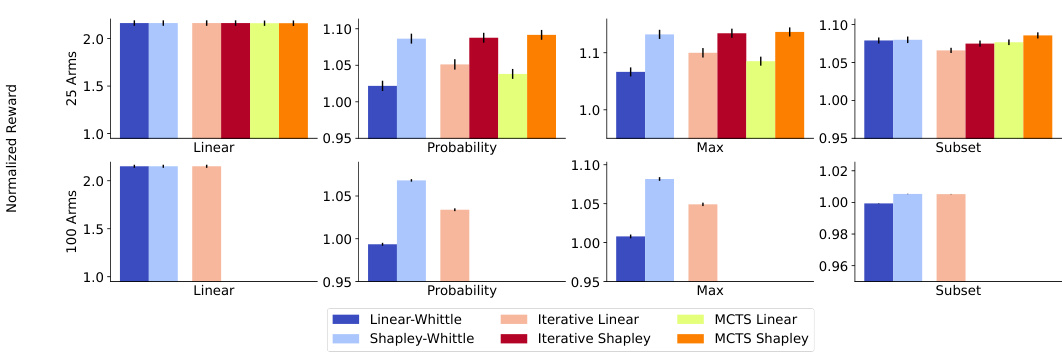
The figure compares the performance of six proposed policies (Linear-Whittle, Shapley-Whittle, Iterative Linear, Iterative Shapley, MCTS Linear, and MCTS Shapley) against six baselines (Random, Vanilla Whittle, Greedy, MCTS, DQN, and DQN Greedy) across four reward functions (Linear, Probability, Max, and Subset) for restless multi-armed bandits with global rewards. The results show that all proposed policies outperform the baselines, and the Iterative and MCTS Shapley-Whittle policies consistently achieve the best performance, often within 3% of the optimal policy for smaller problem sizes (N=4).

The figure compares the performance of several policies (Linear-Whittle, Shapley-Whittle, Iterative Linear, Iterative Shapley, MCTS Linear, MCTS Shapley) against baselines (Random, Vanilla Whittle, Greedy, DQN, DQN Greedy, Optimal) across four different reward functions (Linear, Probability, Max, Subset). The results show that all proposed policies outperform the baselines, with Iterative and MCTS Shapley-Whittle generally achieving the best performance. For smaller problem sizes (N=4), the best performing policy is within 3% of the optimal solution.

This figure compares the performance of several restless bandit algorithms across four different reward functions. The algorithms include baselines (Random, Vanilla Whittle, Greedy, MCTS, DQN, and DQN Greedy) and the authors’ proposed algorithms (Linear-Whittle, Shapley-Whittle, Iterative Linear, Iterative Shapley, MCTS Linear, and MCTS Shapley). The results show that all of the authors’ algorithms outperform the baselines, and the Iterative and MCTS Shapley-Whittle algorithms perform particularly well, achieving near-optimal results in most cases.

This figure compares the performance of various restless multi-armed bandit (RMAB) policies, including baselines and the authors’ proposed adaptive policies, across four different reward functions. The results show that all the authors’ proposed policies consistently outperform the baselines, and that the iterative and Monte Carlo Tree Search (MCTS) Shapley-Whittle policies generally achieve the best performance, coming within 3% of the optimal policy for a problem size of N=4.

Full paper

#