On Tractable $
hi$-Equilibria in Non-Concave Games

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working with non-concave games, a common scenario in machine learning. It offers efficient algorithms for approximating equilibria, addressing a major challenge in the field and opening new avenues for investigating tractable solutions in complex, multi-agent systems. The findings are relevant to GANs, MARL, and other deep learning applications.

Visual Insights

#

This figure illustrates the relationships between various solution concepts in non-concave games. An arrow pointing from one concept to another indicates that the former is a subset of the latter. The concepts shown include Nash Equilibrium (NE), Mixed Nash Equilibrium (MNE), Correlated Equilibrium (CE), Coarse Correlated Equilibrium (CCE), Local Nash Equilibrium, and various types of Φ-equilibria (Finite-Φ, Conv(Φ(δ)), Proj(δ), Int(δ)). The dashed arrow highlights a special case where a Conv(Φ(δ))-equilibrium is a subset of a Finite-Φ-equilibrium if Φ(δ) is finite. The figure is divided into two main sections: Global Deviation and Local Deviation, signifying the type of strategy modifications considered for the Φ-equilibria.

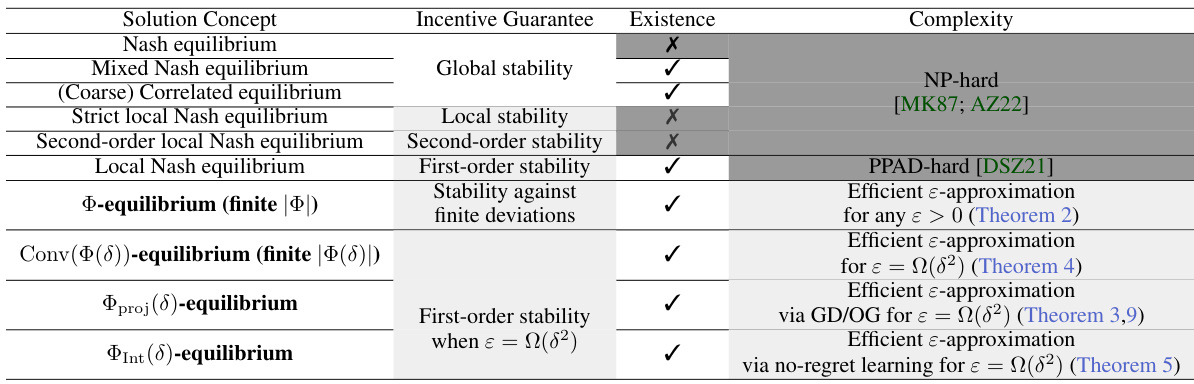
The table compares various solution concepts in multi-player non-concave games, including Nash equilibrium, mixed Nash equilibrium, correlated equilibrium, and local Nash equilibria. It highlights the incentive guarantees, existence, complexity, and approximability of each concept. Details on definitions and a more complete discussion of existence and complexity can be found in Appendix B.

In-depth insights

#

Non-concave Games

#

The concept of “Non-concave Games” signifies a significant departure from traditional game theory, challenging established equilibrium concepts and solution methods. In non-concave games, the players’ utility functions are not concave in their own strategies. This non-concavity introduces several complications, including the potential non-existence of Nash equilibria, the intractability of finding mixed or correlated equilibria, and the infinite support of such solutions. The paper explores alternative solution concepts, such as Φ-equilibria, which guarantee existence even in non-concave games and provides algorithms to approximate such equilibria. The focus on tractable Φ-equilibria for various families of strategy modifications, including local modifications, is a key contribution, offering a potential pathway toward understanding and solving non-concave games. The work highlights the importance of non-concave games in machine learning applications involving deep neural networks, where traditional approaches often fall short.

Phi-Equilibrium

#

The concept of “““Phi-Equilibrium””” offers a compelling alternative solution concept in game theory, particularly useful when dealing with non-concave games where traditional Nash equilibria may not exist or are computationally intractable. Phi-Equilibrium generalizes correlated equilibrium by considering a set of strategy modifications, Φ, for each player. The size and nature of Φ directly impact the strength of the incentive guarantees provided by the equilibrium. A finite Φ allows for efficient computation, while infinite sets, particularly those based on local modifications (like projections or convex combinations of local deviations), offer interesting trade-offs between tractability and the strength of incentive guarantees in non-trivial regimes. The study of Phi-Equilibria effectively expands the range of solution concepts applicable to non-concave games, offering more nuanced and potentially tractable approaches in complex multi-agent settings like those found in machine learning and other domains with non-convex utility functions. Exploring different families of strategy modifications within the framework of Phi-Equilibria provides valuable insights into the computational complexity and incentive properties of various equilibrium notions, shedding light on the inherent challenges in non-concave game theory while simultaneously suggesting avenues for more efficient equilibrium computation.

Local Strategy

#

The concept of “Local Strategy” in game theory signifies a significant departure from traditional approaches that often rely on global equilibrium concepts. Local strategies focus on modifications to a player’s strategy within a constrained neighborhood, thereby addressing the computational intractability associated with finding global equilibria, especially in complex, non-concave games. The paper explores several families of local strategy modifications, including projection-based, convex combination, and interpolation methods. Each approach presents its own challenges and computational properties. The key advantage lies in the guaranteed existence of equilibria under local modifications, even when Nash equilibria are elusive. Moreover, by limiting deviations to local regions, the computational complexity is often reduced, making it tractable to learn and approximate equilibria via decentralized learning dynamics, like online gradient descent or optimistic gradient methods. The study of local strategies opens up new avenues for analyzing non-concave games, which are prevalent in modern machine learning applications, and provides a path towards a more computationally feasible game-theoretic analysis.

Efficient Algorithms

#

The concept of ’efficient algorithms’ in the context of a research paper likely revolves around the development and analysis of computational methods for solving specific problems. Efficiency here is multifaceted, encompassing time complexity (how quickly the algorithm runs), space complexity (how much memory it uses), and potentially energy efficiency. A thoughtful exploration would delve into the algorithm’s design choices—data structures, algorithmic paradigms (e.g., divide-and-conquer, dynamic programming), and optimization techniques used to achieve efficiency. The discussion would likely include a theoretical analysis of the algorithm’s complexity, potentially using Big O notation to characterize its scaling behavior with increasing input size. Additionally, the analysis might involve empirical results demonstrating the algorithm’s performance on real-world data, comparing it to existing approaches to highlight its advantages. Scalability is another key aspect, as an efficient algorithm should gracefully handle large datasets without excessive performance degradation. The paper likely addresses these aspects of algorithm design and evaluation to establish its contributions to the field.

Future Research

#

Future research directions stemming from this work could explore several promising avenues. Extending the efficient algorithms developed for finite and specific infinite strategy modification sets to a broader class of modifications is crucial. This involves investigating the computational complexity of approximating Φ-equilibria under various conditions and developing more general-purpose, efficient algorithms that are not restricted by the specific structure of Φ. Analyzing the convergence rates of the proposed learning algorithms, particularly in non-trivial regimes, could reveal valuable insights into the dynamics of non-concave games and suggest potential improvements to algorithm design. Investigating the relationship between Φ-equilibria and other solution concepts like Nash equilibrium and correlated equilibrium would provide a deeper theoretical understanding of the solution space for non-concave games. Finally, applying these theoretical results to practical machine learning applications involving deep neural networks or multi-agent reinforcement learning is essential. This involves addressing the challenges posed by high dimensionality and non-convexity in real-world scenarios.

More visual insights

#

More on figures

This figure shows the relationships between various solution concepts in non-concave games, including Nash Equilibrium (NE), Mixed Nash Equilibrium (MNE), Correlated Equilibrium (CE), Coarse Correlated Equilibrium (CCE), Local Nash Equilibrium, and different types of Φ-equilibria. An arrow indicates that a solution concept is a subset of another, illustrating the hierarchy of solution concepts and their relationships.

This figure illustrates the difference between two types of local strategy modifications: projection-based and beam-search based. Given a point x and a direction vector -v, ΦProj,v(x) projects x along -v until it hits the boundary of the feasible set. ΦBeam,v(x) moves from point x along the direction of -v to the maximum extent possible within the feasible set. The figure shows that the modifications can lead to different points, which impacts the approximation of equilibria.

More on tables

This table compares various solution concepts in multi-player non-concave games, including Nash equilibrium, mixed Nash equilibrium, correlated equilibrium, and local Nash equilibria. It highlights whether each concept guarantees incentive compatibility, its existence, complexity, and the possibility of efficient approximation algorithms.

This table compares different solution concepts in multi-player non-concave games, including Nash equilibrium, mixed Nash equilibrium, correlated equilibrium, and local Nash equilibria. It summarizes their incentive guarantees, existence, stability properties, and computational complexity, highlighting the challenges posed by non-concave games and motivating the need for alternative solution concepts like Φ-equilibria.

Full paper

#