↗ OpenReview ↗ NeurIPS Homepage ↗ Hugging Face ↗ Chat
TL;DR#
Offline reinforcement learning (RL) trains agents using pre-collected data, but faces challenges in estimating values of unseen behaviors. Model-based methods address this by creating synthetic data through model rollouts. However, a common practice of truncating rollouts to prevent error accumulation creates ’edge-of-reach’ states, where value estimations are bootstrapped from the void, leading to value overestimation and performance collapse. This is the central problem that the paper addresses.
The paper introduces Reach-Aware Value Learning (RAVL), a novel method directly tackling the edge-of-reach problem by identifying and preventing value overestimation in these critical states. Unlike existing methods, RAVL maintains high performance even when given perfect dynamics models, making it more reliable and robust than previously proposed methods. This is achieved by applying a simple value pessimism technique that mitigates the impact of edge-of-reach states. The results demonstrate that RAVL significantly outperforms existing methods on standard offline RL benchmarks.
Key Takeaways#
Why does it matter?#
This paper is crucial because it identifies a critical oversight in offline model-based reinforcement learning (RL). Existing methods fail as model accuracy improves, a problem this research solves. It opens new avenues for more robust offline RL, vital for various applications where online data collection is costly or dangerous. This work is relevant to researchers tackling issues of sample efficiency and safety in RL.
Visual Insights#
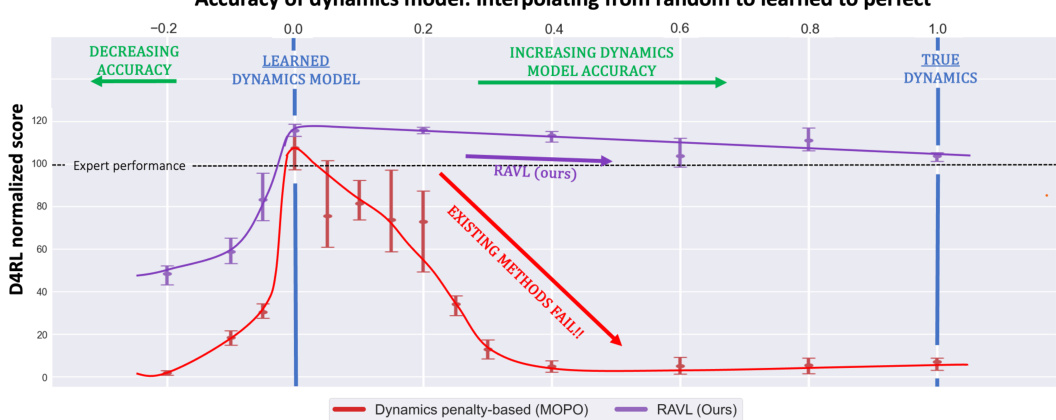
This figure shows the performance of existing offline model-based reinforcement learning methods and the proposed RAVL method as the accuracy of the dynamics model is increased. The x-axis represents the interpolation between a random model, a learned model, and the true dynamics model. The y-axis represents the D4RL normalized score. The figure demonstrates that existing methods fail when the dynamics model is perfect (true dynamics), while RAVL remains robust.

This table presents a comprehensive comparison of the proposed RAVL algorithm against other state-of-the-art methods on the standard D4RL MuJoCo benchmark. The results demonstrate that RAVL achieves comparable performance to the best existing methods, while being significantly more robust to the absence of model uncertainty. The table highlights the mean and standard deviation of the final performance for each algorithm across six different seeds, providing strong statistical support for the claims made in the paper.
In-depth insights#
Offline RL Failure#
Offline reinforcement learning (RL) aims to learn policies from pre-collected data, avoiding costly and risky online data collection. A significant challenge is that offline RL algorithms struggle to accurately estimate the value of actions not present in the dataset. Model-based methods attempt to overcome this by using a learned dynamics model to generate synthetic data. However, this paper reveals a critical failure mode: when these methods are given a perfect dynamics model (no model errors), their performance collapses. This exposes a previously unrecognized limitation, termed the ’edge-of-reach’ problem. The core issue is that training involves limited-horizon rollouts from the dataset, leading to the existence of ’edge-of-reach’ states—states only reachable at the very end of a rollout. These states are used as targets in value updates but are never themselves updated, triggering pathological overestimation and ultimately, failure. The findings challenge prevailing theoretical assumptions, demonstrating that the failure isn’t solely due to model inaccuracies. Instead, it highlights a critical limitation related to the fundamental design of current model-based methods and the way they interact with finite datasets. This new understanding is crucial for developing more robust and reliable offline RL algorithms.
Edge-of-Reach Issue#
The “Edge-of-Reach” issue, a novel problem identified in offline model-based reinforcement learning (RL), arises from the truncation of model rollouts. Existing methods, assuming that performance gaps stem solely from model inaccuracies, fail when presented with perfect dynamics. The core problem is that edge-of-reach states, reachable only in the final rollout step, are used as targets for Bellman updates but are never updated themselves. This leads to pathological value overestimation and complete performance collapse. The paper highlights the critical oversight in assuming full-horizon rollouts, contrasting with the practical necessity of truncated rollouts to prevent accumulating model errors. Addressing this “bootstrapping from the void” is crucial for robust offline RL, especially considering the inevitable improvement of world models in the future. Reach-Aware Value Learning (RAVL) is proposed as a solution that directly addresses the edge-of-reach problem through value pessimism, maintaining stability even with perfect dynamics, unlike existing approaches.
RAVL Solution#
The RAVL solution tackles the edge-of-reach problem in offline model-based reinforcement learning by directly addressing the issue of value misestimation at states that are only encountered at the end of truncated rollouts. Unlike prior methods, which primarily handle model inaccuracies through uncertainty penalties that vanish when using a perfect dynamics model, RAVL uses value pessimism via an ensemble of Q-functions. This approach effectively detects and penalizes overestimation at these edge-of-reach states, preventing catastrophic failure even as the model improves. The method’s simplicity and robustness are demonstrated through experiments, showing strong performance on standard benchmarks and stability across hyperparameters, a significant step towards creating more robust and reliable offline RL agents.
Unified RL View#
A unified RL view seeks to bridge the gap between model-based and model-free offline reinforcement learning methods. Model-free methods typically address the out-of-sample action problem through conservatism, while model-based methods leverage learned dynamics models for synthetic data generation. A unified perspective reveals that both approaches implicitly grapple with the core issue of value misestimation due to limited data coverage and horizon truncation. The edge-of-reach problem, a key insight, highlights how model-based methods, despite their focus on model accuracy, can still fail due to states only reachable after k-step rollouts, leading to catastrophic overestimation. A unified approach would recognize that both model-free and model-based methods suffer from similar fundamental limitations regarding out-of-distribution states and actions, offering a chance for developing more robust and generalized offline RL algorithms.
Future Offline RL#
Future offline reinforcement learning (RL) research should prioritize addressing the edge-of-reach problem, a critical oversight in current model-based methods. This problem arises from the truncation of model rollouts, leading to pathological value overestimation and performance collapse, even with perfect dynamics models. Future work must focus on robust methods that explicitly handle edge-of-reach states, such as Reach-Aware Value Learning (RAVL) or similar techniques. Furthermore, research should explore unified frameworks that bridge the gap between model-based and model-free offline RL, leveraging the strengths of both approaches to address the limitations of each. This will require addressing out-of-distribution action problems and developing effective methods for handling uncertainty in both dynamics and reward models. Finally, extensive empirical evaluation on diverse and challenging benchmarks is crucial to ensure the generalizability and robustness of future offline RL algorithms. Improving dynamics models alone is insufficient; a more comprehensive solution necessitates robust value estimation techniques.
More visual insights#
More on figures
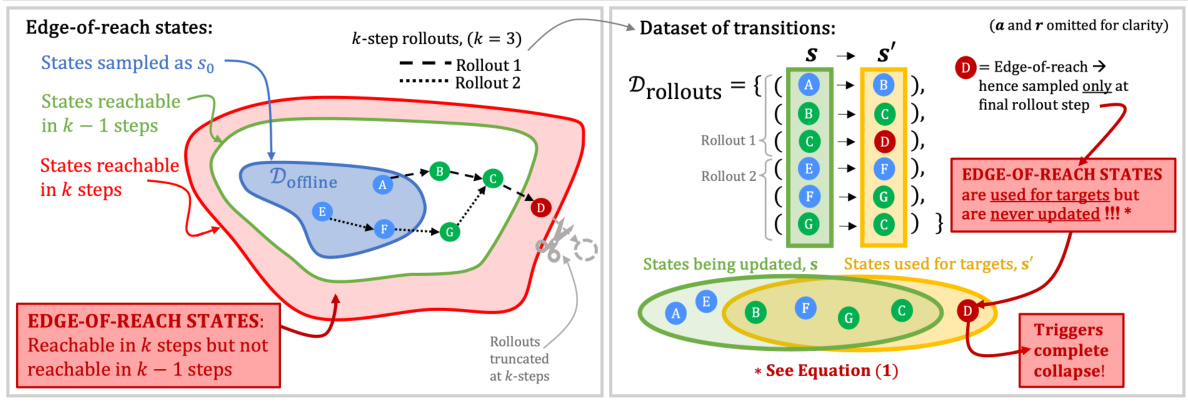
This figure illustrates the edge-of-reach problem in offline model-based reinforcement learning. The left panel shows how k-step rollouts from a fixed dataset can lead to states (edge-of-reach states) that are only reachable in the final step of a rollout and are never updated during training. The right panel shows how this affects the Bellman update, leading to value overestimation and performance collapse. The figure highlights the difference between states that are updated (because they are reachable in less than k steps) and states that are used for targets but never updated (edge-of-reach states).
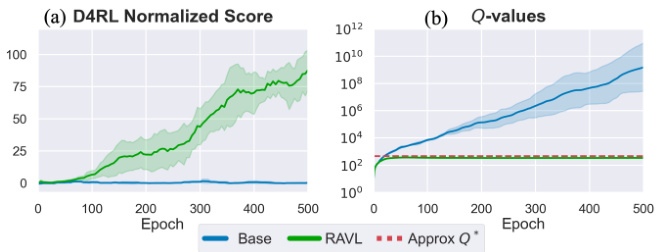
This figure shows the results of the base offline model-based RL algorithm on the D4RL Walker2d-medexp benchmark. The left panel shows the normalized score over training epochs, indicating that the algorithm fails to learn a good policy. The right panel shows the Q-values over training epochs, illustrating a dramatic, exponential increase that signifies pathological value overestimation. This comparison highlights the significant performance degradation and instability of the base method, which serves as a key motivation for introducing the proposed RAVL algorithm.
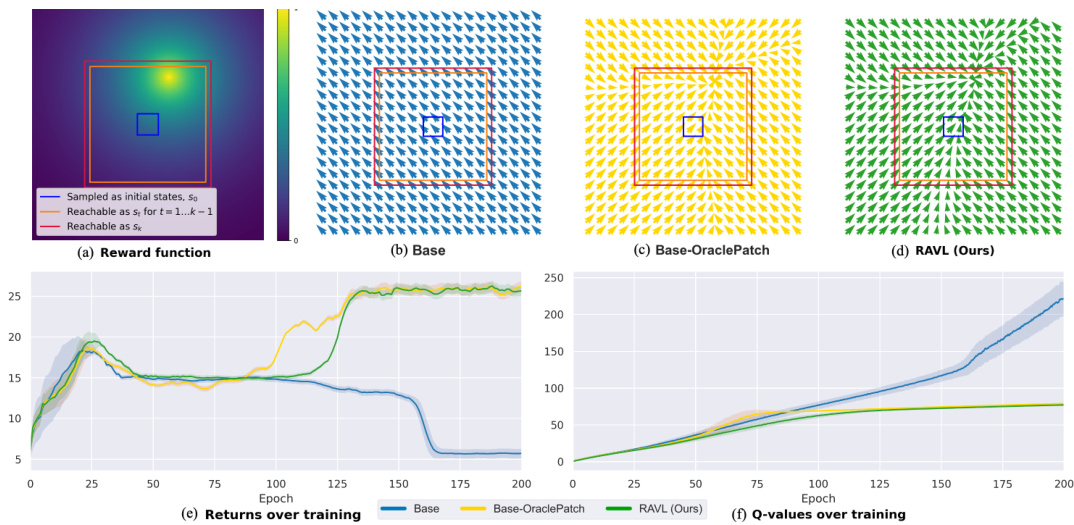
This figure shows the results of experiments conducted on a simple environment designed to isolate the edge-of-reach problem. It compares four different approaches: the base model-based offline RL method (which fails), a version of the base method where oracle Q-values are patched into edge-of-reach states (which succeeds), and RAVL (the proposed solution, which also succeeds). The visualization includes reward functions, final policies, training returns, and Q-value evolution over training. This illustrates that the edge-of-reach problem is causing the failures of base methods, and that RAVL successfully addresses the problem by preventing overestimation of values in the edge-of-reach states.
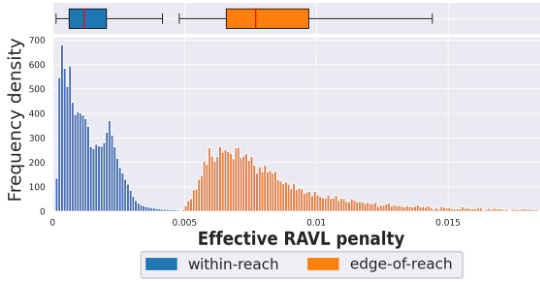
This figure shows the distribution of the effective RAVL penalty for within-reach and edge-of-reach states in the simple environment described in Section 4. The box plot summarizes the distribution, while the histogram provides a more detailed view. As intended, the penalty is significantly higher for edge-of-reach states than for within-reach states, demonstrating that RAVL successfully identifies and penalizes these critical states.
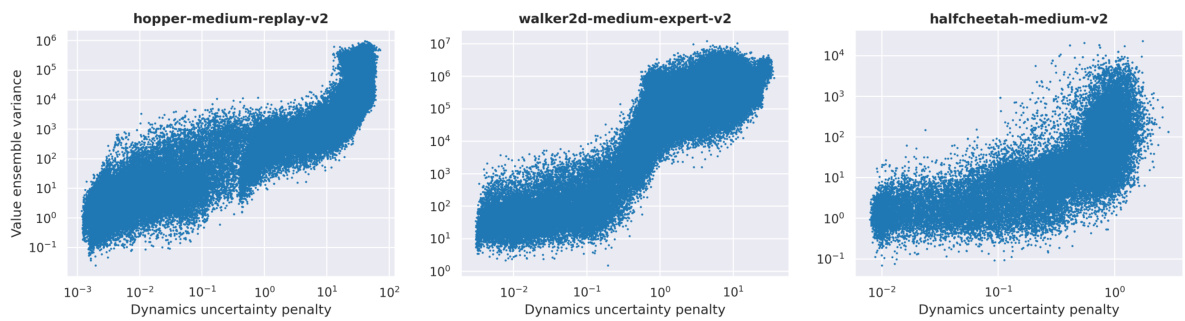
This figure shows the positive correlation between the dynamics uncertainty penalty used in MOPO and the variance of the value ensemble in RAVL. This suggests that existing methods, which focus on dynamics uncertainty, might indirectly address the edge-of-reach problem, even without explicitly acknowledging it. The correlation coefficients provided quantify the strength of this relationship across three different D4RL benchmark environments.

This figure visualizes the rollouts sampled during training in a simple environment for three different methods: the base method, Base-OraclePatch (which uses oracle Q-values to correct for edge-of-reach states), and RAVL. It shows how the base method’s rollouts are increasingly concentrated in edge-of-reach states (red), leading to its failure. Base-OraclePatch successfully avoids this issue by using oracle values. RAVL mimics the behavior of Base-OraclePatch, indicating its effectiveness in addressing the edge-of-reach problem.
More on tables
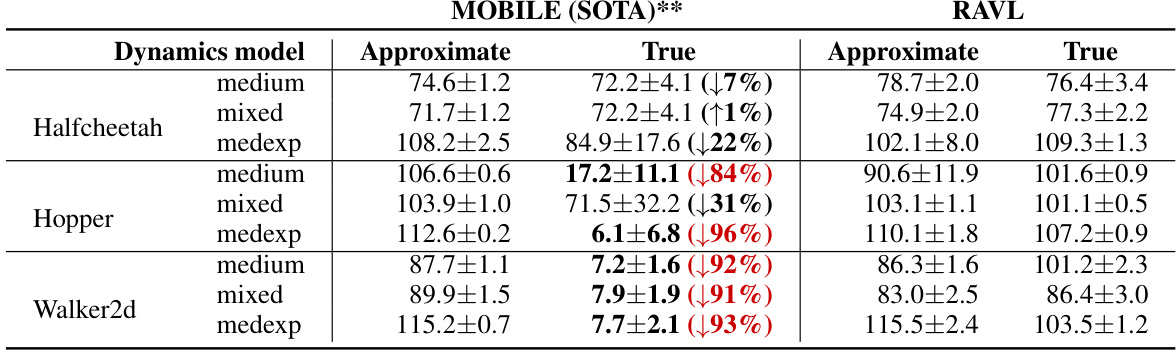
This table presents the performance of existing model-based offline reinforcement learning methods and the proposed RAVL method when using the true dynamics (zero error, zero uncertainty). It demonstrates the failure of existing methods under perfect dynamics, highlighting the importance of addressing the edge-of-reach problem. RAVL, in contrast, maintains high performance even with perfect dynamics, illustrating its robustness.
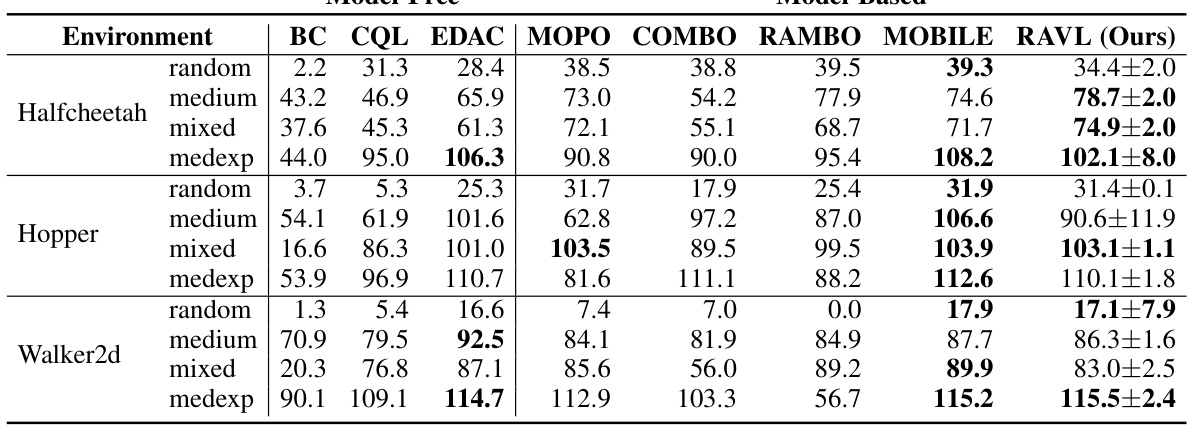
This table presents a comparison of the performance of RAVL against other state-of-the-art offline reinforcement learning algorithms on the D4RL MuJoCo benchmark. The results are averaged over six seeds and show the mean and standard deviation of the final performance. A key highlight is that RAVL performs competitively even in the absence of model uncertainty, unlike other methods that rely on dynamics penalization, showcasing its robustness and effectiveness.

This table presents the results of experiments conducted on the D4RL MuJoCo v2 datasets using both approximate and true dynamics models. It compares the performance of RAVL and existing model-based methods that rely on dynamics uncertainty penalties. A key finding is that existing methods fail when using the true dynamics, unlike RAVL which performs well. This demonstrates RAVL’s robustness and its ability to address the edge-of-reach problem, a novel issue identified in the paper.
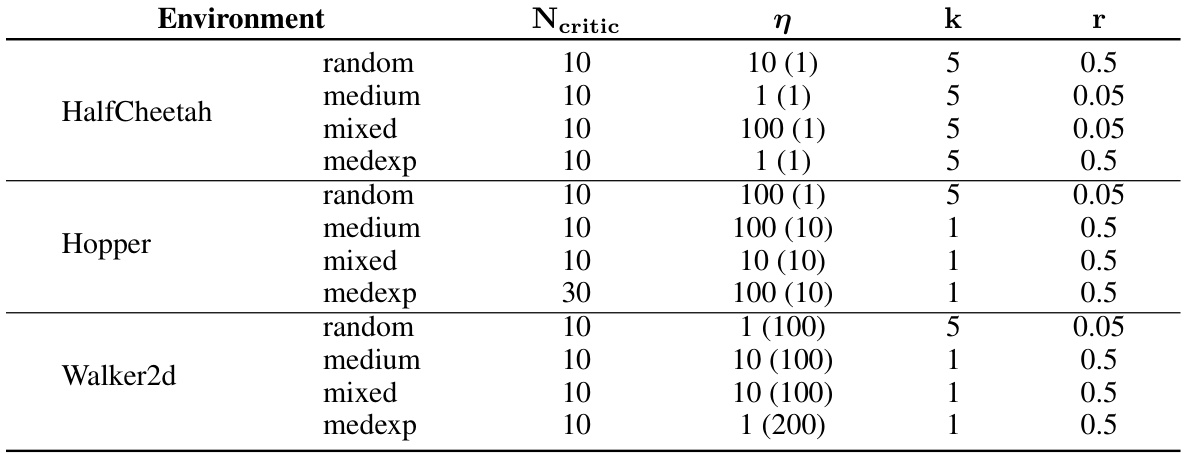
This table shows the hyperparameter settings used for RAVL in the D4RL MuJoCo locomotion experiments. It lists the values for four hyperparameters: Ncritic (number of Q-ensemble elements), η (ensemble diversity weight), k (model rollout length), and r (real-to-synthetic data ratio). Different values were used for the experiments with learned dynamics (Table 2) and for experiments with uncertainty-free dynamics (Table 1), where only η was tuned. The values in parentheses indicate the settings used for the uncertainty-free dynamics experiments.

This table lists the fixed hyperparameters used in the Reach-Aware Value Learning (RAVL) method for the Deep Data-Driven Reinforcement Learning (D4RL) MuJoCo locomotion tasks. These are the hyperparameters that were held constant across all experiments in the paper. These hyperparameters include the number of training epochs, the discount factor (gamma), the learning rate, batch size, buffer retain epochs, and the number of rollouts used in the training process. The values of these hyperparameters were determined through preliminary experiments and are reported as fixed for reproducibility and to ensure a fair comparison between RAVL and other methods.

This table lists the hyperparameters used for the Reach-Aware Value Learning (RAVL) algorithm when applied to the V-D4RL DeepMind Control Suite tasks. The hyperparameters cover various aspects of the model, including ensemble size, imagination horizon, batch size, sequence length, action repeat, observation size, discount factor, optimizer, learning rates, training epochs for both the model and agent, uncertainty penalty type, uncertainty weight, and the number of critics used. These settings are crucial for the algorithm’s performance and stability.

This table presents the penalty terms used by three popular offline model-based reinforcement learning algorithms: MOPO, MOREL, and MOBILE. The table shows that all three algorithms utilize penalties based on estimated dynamics model uncertainty. Importantly, the table demonstrates that when the dynamics model is the true model (and thus there is no uncertainty), the penalty terms all collapse to zero.

This table compares the per-step rewards obtained using the base offline model-based method with those from the true dynamics. The similarity in rewards suggests that model exploitation is not the primary cause of the value overestimation problem, as existing methods suggest. This supports the paper’s argument that the edge-of-reach problem is a more significant factor.

This table presents the results of RAVL and baseline methods on the pixel-based V-D4RL benchmark. It shows that RAVL improves performance on the medium and medexp level datasets, which are less diverse, suggesting that the edge-of-reach problem is more prominent in less diverse environments. The results also demonstrate that RAVL generalizes well to latent-space settings, which are used by the baseline DreamerV2 algorithm.

This table compares the performance of RAVL against other state-of-the-art methods on the D4RL MuJoCo benchmark. It shows mean and standard deviation of final performance across six seeds for various environments (Halfcheetah, Hopper, Walker2d) and dataset conditions (random, medium, mixed, medexp). Notably, it highlights RAVL’s performance even without explicit dynamics penalization, demonstrating its effectiveness in the absence of model uncertainty, a scenario where other methods fail.

This table shows the results of ablations on RAVL’s diversity regularizer hyperparameter η. The results show minimal change in performance with a sweep across two orders of magnitude, indicating that RAVL is robust and can be applied to new settings without much tuning. The table includes results for Halfcheetah medium and Halfcheetah mixed environments.
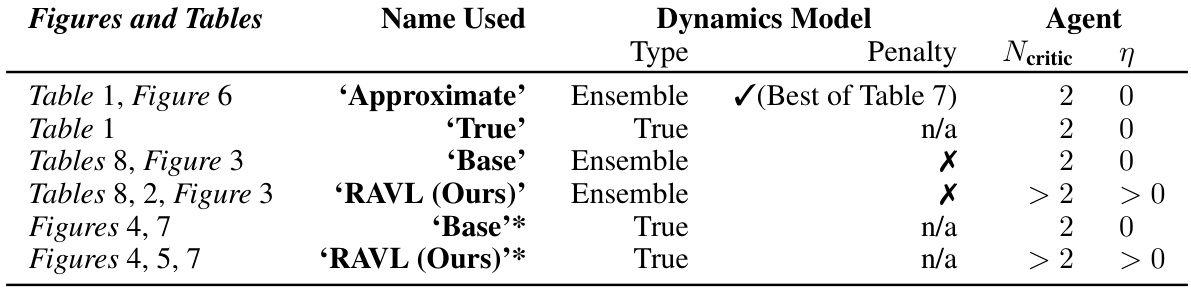
This table summarizes the different experimental setups used throughout the paper to compare various offline model-based reinforcement learning methods. It specifies for each experiment the name used, the type of dynamics model (approximate ensemble or true dynamics), the presence of any penalty (dynamics uncertainty penalty, or none), and the hyperparameters of the agent (size of the Q-ensemble and ensemble diversity regularizer). Different setups are used to isolate the edge-of-reach problem and test the effectiveness of the proposed method (RAVL) under different conditions.
Full paper#