↗ OpenReview ↗ NeurIPS Homepage ↗ Hugging Face ↗ Chat
TL;DR#
Many studies of Large Language Model (LLM) mechanisms focus on a single model snapshot, limiting the understanding of how these mechanisms evolve during training and scale. This raises concerns about the generalizability of such findings to real-world scenarios where LLMs continuously undergo training and are deployed at various scales. This paper tackles this problem by tracking the evolution of model mechanisms, operationalized as circuits, across 300 billion tokens of training and across decoder-only LLMs with varying parameter sizes. The researchers aimed to investigate whether the insights derived from circuit analyses conducted on small models remain applicable after further training or across different model scales.
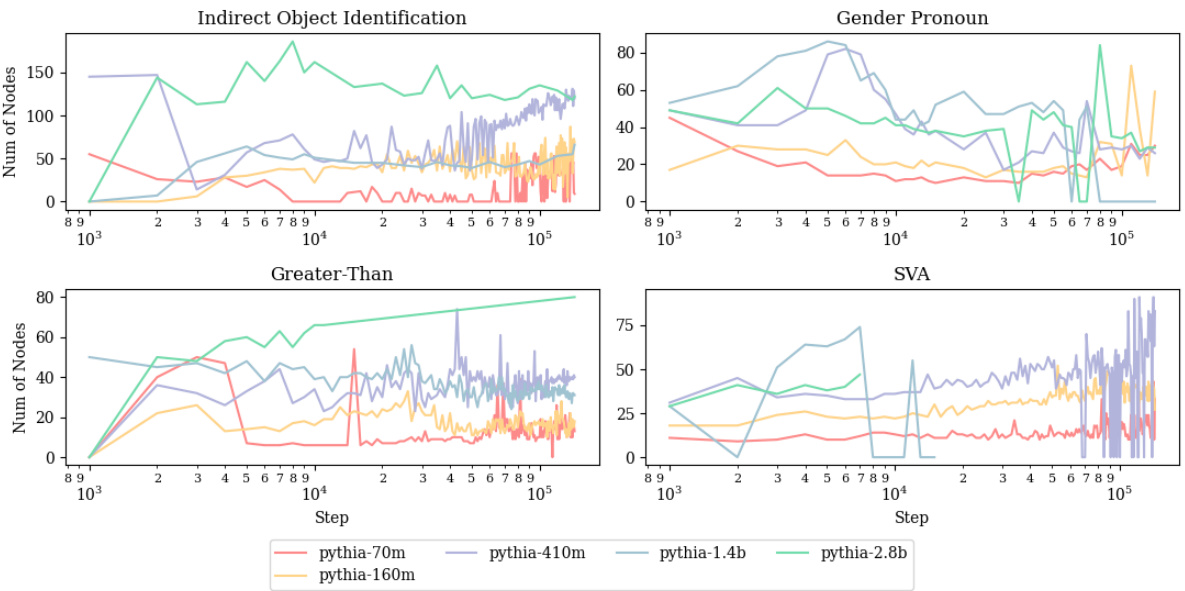
The study demonstrates that task abilities and functional components supporting these tasks emerge at remarkably consistent token counts across model scales. While the specific components implementing these algorithms may change over time, the overarching algorithms themselves remain stable. This remarkable consistency holds even when comparing small and large models. Interestingly, the study finds a positive correlation between circuit size and model size. Although circuit size can fluctuate over time, it does not hinder the continued consistent implementation of the same algorithms. These findings suggest that insights from circuit analyses conducted on smaller models early in training can reliably predict behavior of larger models even after further training. This research contributes to a more robust and efficient approach to understanding LLM mechanisms.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in mechanistic interpretability as it demonstrates the generalizability of circuit analysis across various model scales and training stages. It challenges existing assumptions about the limitations of studying smaller models, thus paving the way for more efficient and scalable interpretability research. The findings also provide valuable insights into the stability and evolution of algorithmic mechanisms within LLMs, which is essential for understanding their capabilities and limitations.
Visual Insights#

This figure shows the performance of various sized language models (Pythia-70m, Pythia-160m, Pythia-410m, Pythia-1.4b, Pythia-2.8b, Pythia-6.9b, Pythia-12b) on four different tasks (Indirect Object Identification, Gendered Pronoun, Greater-Than, Subject-Verb Agreement) over the course of their training (measured in tokens seen). The x-axis represents the number of tokens the model has processed, and the y-axis represents the model’s performance on the task. The plot shows that despite the significant differences in model size, the models tend to achieve peak performance at roughly the same number of tokens processed across various tasks, demonstrating a similarity in task acquisition rate across different scales.
In-depth insights#
LLM Circuit Evolution#
LLM Circuit Evolution examines how the internal computational pathways (circuits) of large language models (LLMs) change during training. The core finding is that while individual components within circuits may shift or even disappear over time, the overall algorithms implemented by the circuits often remain remarkably stable. This suggests a level of robustness and generalization in how LLMs develop their internal mechanisms. Circuit analyses performed on smaller models may provide insights that generalize to larger, more extensively trained models. Furthermore, the study highlights that circuit size is correlated with model scale, indicating that larger models tend to have more complex circuits. The research also reveals that the emergence of functional components in circuits correlates with the acquisition of task abilities, suggesting a direct link between internal circuit development and observable model performance. However, the study focuses on a specific set of tasks, model architectures, and training datasets, and more research is required to confirm whether these findings generalize across diverse scenarios.
Circuit Algorithm Stability#
The concept of “Circuit Algorithm Stability” in the context of large language models (LLMs) is crucial. It investigates whether the underlying computational processes, represented as circuits, remain consistent despite changes in the model’s components. Stability suggests the algorithms themselves are robust and generalize across different training stages and model scales. The study reveals that while individual components (like attention heads) might change, the overarching algorithms they implement often remain consistent over time and across different model sizes. This implies that circuit analysis on smaller, less computationally expensive models can provide valuable insights into the mechanisms of larger, more complex models, improving the scalability of mechanistic interpretability research. However, there is some fluctuation, especially at early training stages and in smaller models, before they stabilize. The research also highlights how model performance can remain stable even if individual components shift or cease contributing, suggesting inherent redundancy and self-repair mechanisms in LLMs. This understanding of both stability and variability is vital for building more robust and interpretable LLMs.
Scale & Training Effects#
Analyzing the effects of scale and training on large language models (LLMs) reveals crucial insights into their capabilities and limitations. Increased model scale generally correlates with improved performance, but this improvement isn’t always linear. A certain scale may be reached where additional parameters offer diminishing returns, highlighting the importance of efficient model design. Similarly, longer training often leads to enhanced performance, but excessive training can sometimes result in overfitting or even performance degradation in certain tasks. The interaction between scale and training duration is complex, with optimal training length potentially varying across model sizes. Understanding this interplay is essential for developing cost-effective and high-performing LLMs. The emergence of critical functional components within the model’s architecture often shows consistent timing across different scales, suggesting some degree of algorithmic universality in how LLMs learn. However, the specific implementation of these components (e.g., specific attention heads) may shift over time and vary across models. Research focusing on the consistency of underlying algorithms despite changes in component implementation is crucial, as it can provide insights into how these models generalize across training and scale.
Circuit Generalizability#
Circuit generalizability explores whether insights from analyzing neural network mechanisms in smaller, simpler models translate to larger, more complex ones. The core question is whether circuits, defined as computational subgraphs explaining specific task-solving mechanisms, exhibit similar structures and behaviors across vastly different model sizes and training durations. A positive answer would significantly impact mechanistic interpretability research, enabling scientists to study simpler models as proxies for understanding more complex systems. However, the existence and fidelity of circuits might vary, and some may disappear during training. Furthermore, the algorithms implemented by these circuits could change despite their similar functionalities. Therefore, evaluating the algorithm’s stability and consistency is crucial in assessing circuit generalizability. This analysis would not only benefit mechanistic interpretability research but also enhance the efficient and cost-effective study of complex models’ behaviors.
Future Research#
Future research should prioritize expanding the scope of models and tasks investigated. The current study’s findings, while compelling, are based on a limited set of tasks and models, primarily from the Pythia suite. Exploring more complex tasks that require a broader range of algorithmic solutions will reveal if the observed stability and generalizability of circuits persist. Additionally, investigating diverse model architectures beyond autoregressive language models will determine the extent to which the findings are architecture-dependent. A crucial aspect of future work involves developing more robust methods for verifying circuit completeness and faithfulness. The current methods, while effective, leave room for improvement in definitively establishing the causal relationship between circuit components and task performance. Further investigation into the mechanisms underlying algorithmic stability is also essential. While the study suggests algorithmic stability despite component-level fluctuations, a deeper understanding of these processes, potentially involving self-repair and load-balancing mechanisms, is needed. Finally, exploring how the observed trends in circuit formation and behavior scale to even larger models, and the relationship between circuit size and model capability, warrants further research. Addressing these research directions will provide a more comprehensive and generalizable understanding of large language model mechanisms.
More visual insights#
More on figures
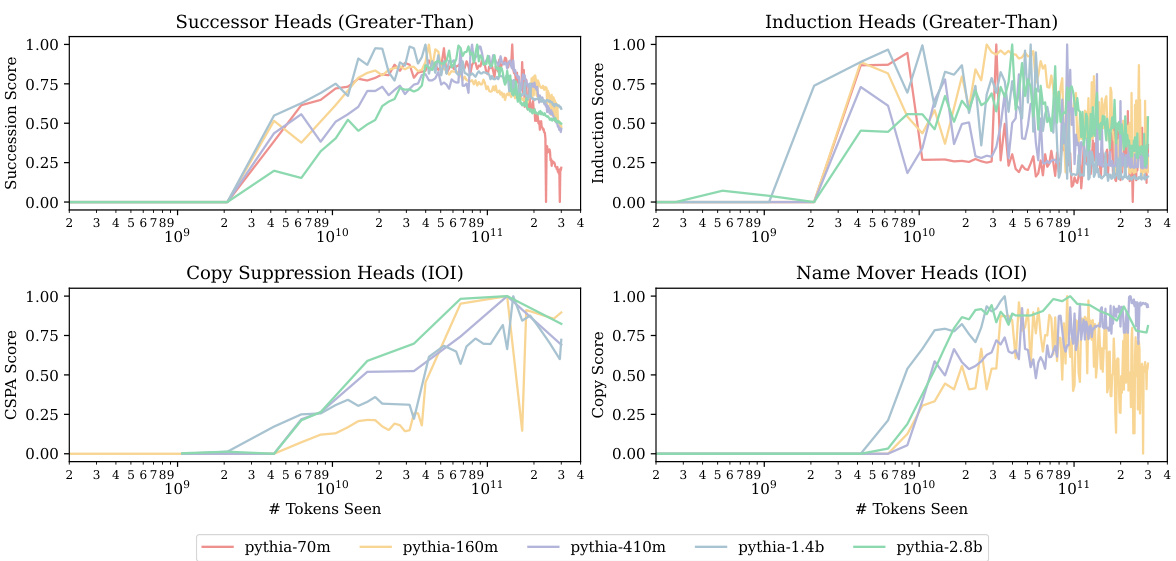
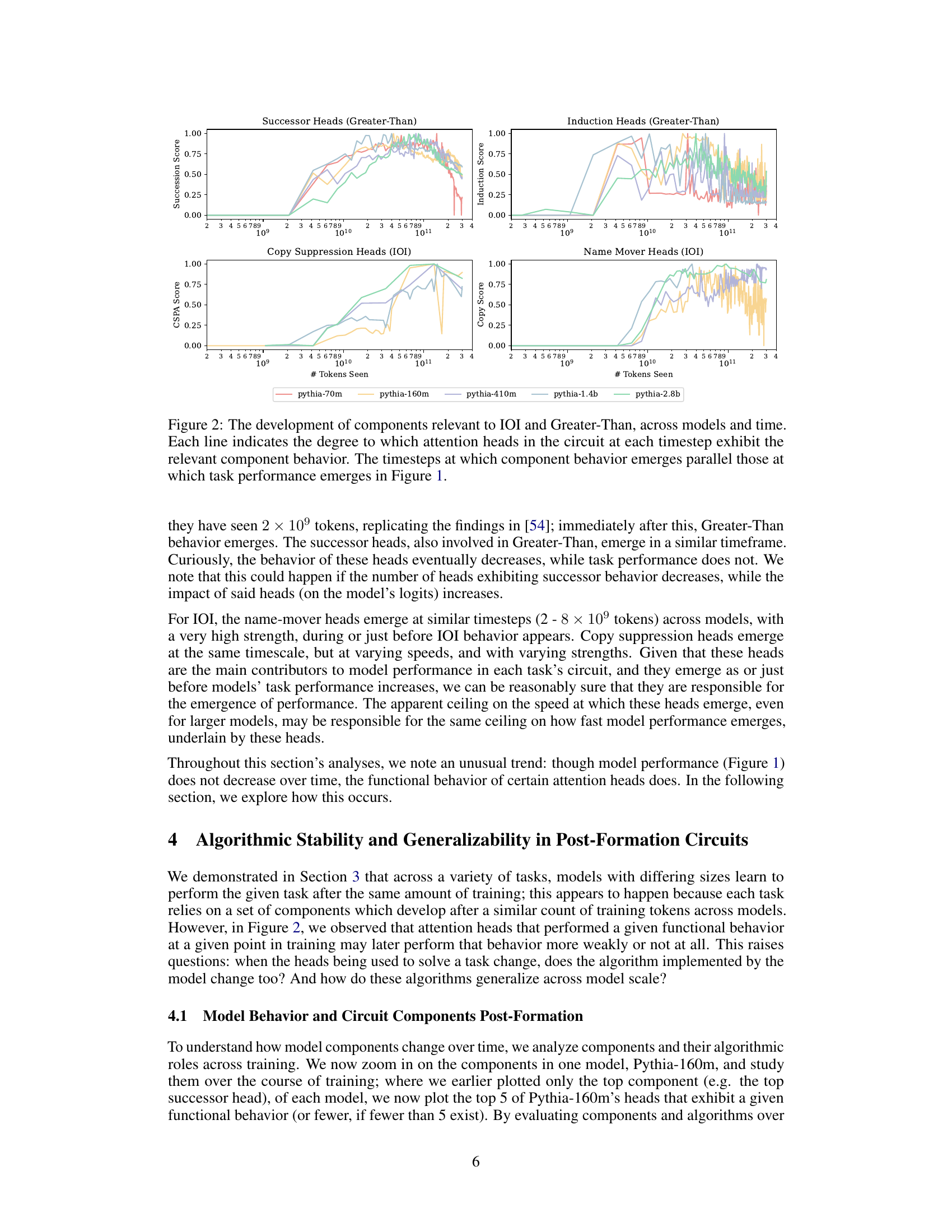
This figure shows the emergence of four attention head types (Successor, Induction, Copy Suppression, and Name Mover Heads) over the course of training in five different sized models. The y-axis represents the component score (a measure of how strongly each head exhibits the given behavior) and the x-axis represents the number of tokens seen during training. The figure demonstrates that these components tend to emerge at similar points in training across all model sizes, mirroring the timing of task acquisition shown in Figure 1.

This figure shows the development of four key attention head components (Successor Heads, Induction Heads, Copy Suppression Heads, and Name Mover Heads) over time and across different model sizes. Each line represents a specific attention head within a model’s circuit, showing the degree to which it exhibits the behavior characteristic of that component type. The x-axis represents the number of tokens seen during training, while the y-axis shows the component score (a metric quantifying the degree of component behavior). The figure demonstrates that the emergence of these components closely parallels the emergence of task performance (as shown in Figure 1), suggesting a strong relationship between the presence of these components and the model’s ability to perform the IOI and Greater-Than tasks. It highlights the consistency of component emergence across model scales.
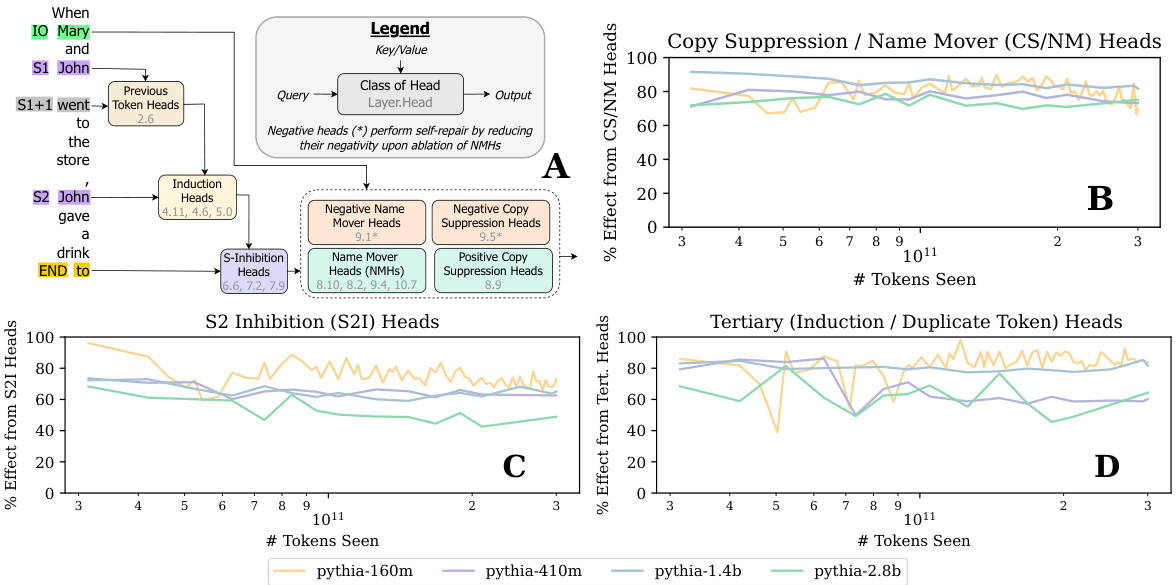
The figure shows the IOI circuit for the Pythia-160m model at the end of its training, along with three additional plots. Plot A is a visual representation of the circuit, highlighting the various attention heads involved and their connections. Plots B, C, and D quantitatively analyze the contribution of different circuit components to the overall model performance. Specifically, plot B assesses the importance of the Copy Suppression and Name-Mover Heads, plot C examines the impact of S-Inhibition Heads, and plot D analyzes the role of Tertiary (Induction/Duplicate Token) Heads. These plots provide a detailed breakdown of how various parts of the IOI circuit contribute to the task.

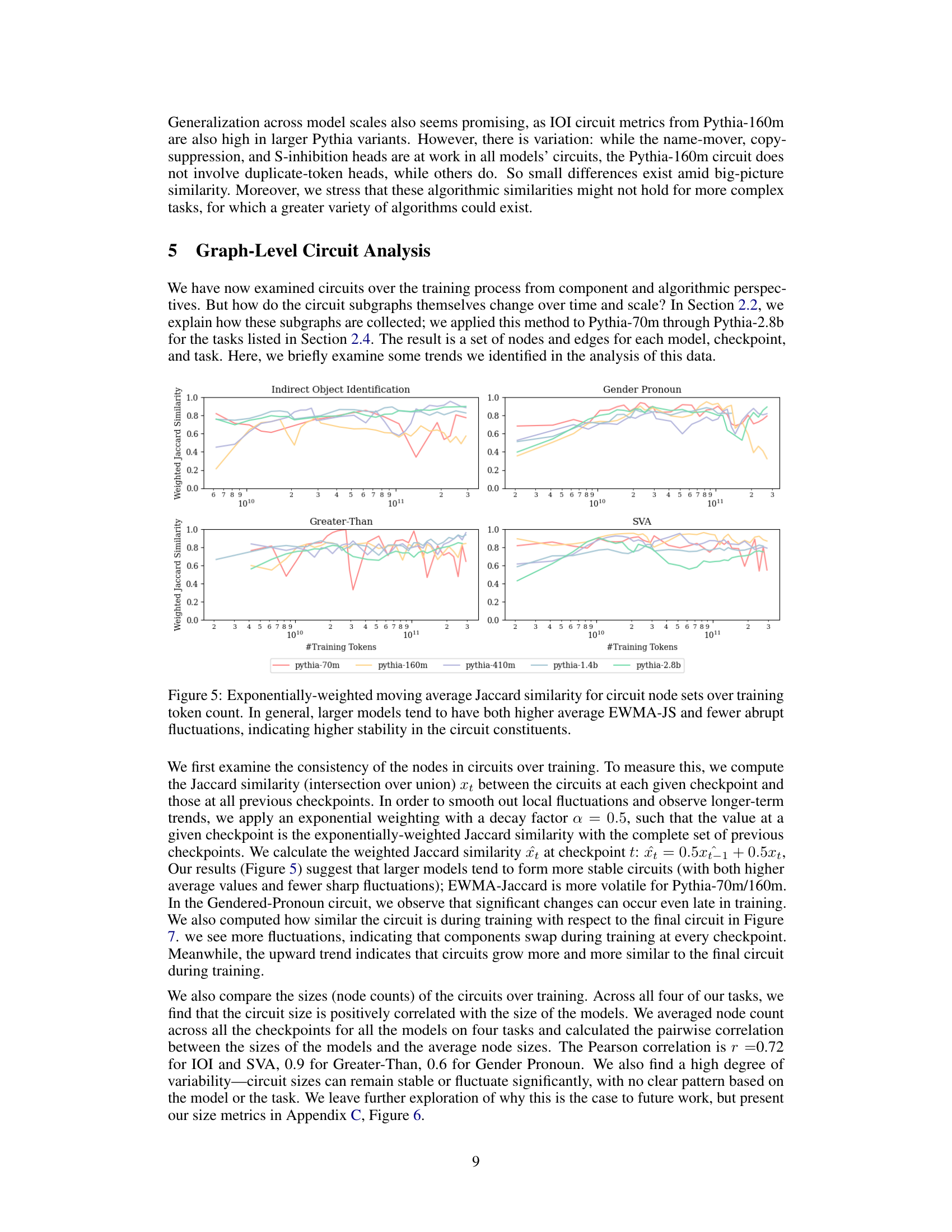
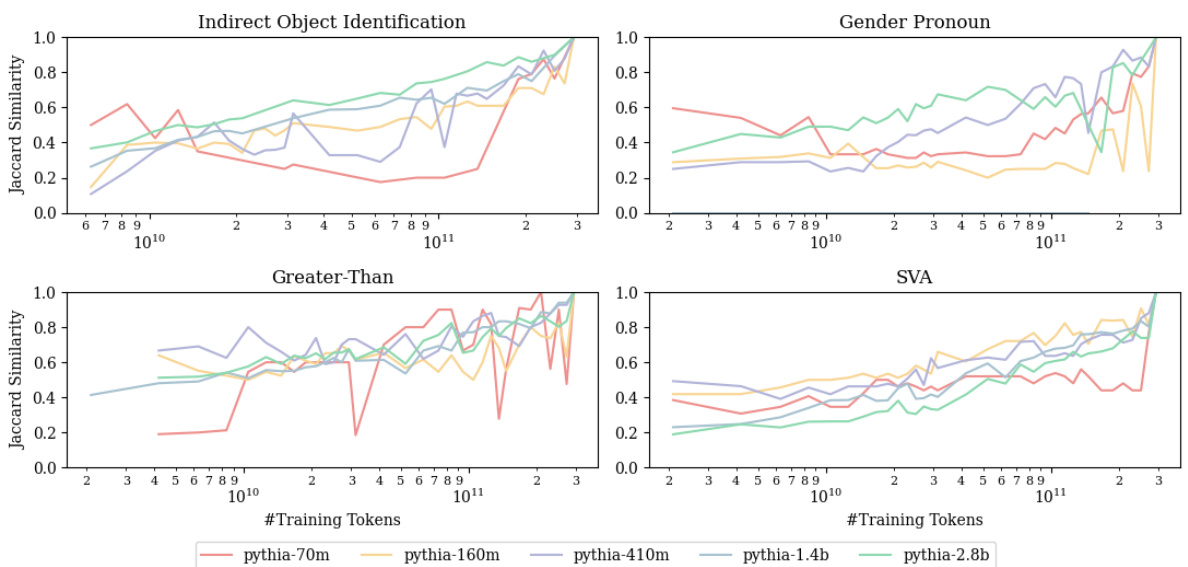
This figure displays the exponentially weighted moving average Jaccard similarity for the circuit node sets over training token counts for different sized models. The Jaccard similarity measures the overlap between the circuit nodes at a given checkpoint and those at all previous checkpoints. The exponential weighting smooths out short-term fluctuations to reveal longer-term trends. Larger models exhibit higher average Jaccard similarity and fewer sharp fluctuations, indicating greater stability and consistency in their circuit composition over the course of training.
This figure displays the performance of different sized language models (70M to 12B parameters) on four different tasks over the course of 300 billion tokens of training. Each line represents a different model size. The x-axis represents the number of tokens processed during training, and the y-axis shows the model’s performance on each task. The key observation is that despite differences in model size, the models reach peak performance at roughly the same number of training tokens. This suggests that the acquisition of task abilities happens at similar stages of training regardless of model scale.
This figure shows the performance of different sized language models (Pythia-70m, Pythia-160m, Pythia-410m, Pythia-1.4b, Pythia-2.8b, Pythia-6.9b, Pythia-12b) on four different tasks (Indirect Object Identification, Gendered Pronoun, Greater-Than, Subject-Verb Agreement) over the course of their training (300 billion tokens). The x-axis represents the number of tokens seen during training, and the y-axis represents the model’s performance on each task, with higher values indicating better performance. The figure demonstrates that across different model sizes and tasks, the models achieve peak performance at similar token counts, suggesting a consistency in learning behavior.

This figure displays the performance of various sized language models on four different tasks over the course of their training. The x-axis represents the number of tokens processed during training, while the y-axis shows the model’s performance on each task. The figure demonstrates that regardless of model size (parameters), models tend to reach peak performance at a similar number of training tokens. This suggests a consistency in how these models acquire task abilities, indicating that model scaling does not necessarily lead to drastically faster learning.

This figure displays the performance of different sized language models on four different tasks over the course of their training. Each line represents a different model size, from 70 million to 12 billion parameters. The x-axis represents the number of tokens processed during training, and the y-axis represents the model’s performance on each task. The key observation is that despite the differences in model size, the models achieve similar levels of performance on each task at roughly the same number of training tokens. This suggests a degree of consistency in how models learn these tasks regardless of scale.
Full paper#