Multidimensional Fractional Programming for Normalized Cuts

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it presents a novel and efficient approach to solve the Normalized Cut problem, a fundamental challenge in unsupervised clustering. The proposed multidimensional fractional programming method offers significant improvements over existing techniques, particularly in handling multi-class clustering and achieving better convergence. This opens new avenues for research in graph-based clustering and related areas, with potential applications in various domains such as image segmentation and community detection. The method’s superior performance and efficiency makes it a valuable tool for researchers working with large-scale datasets. Its theoretical grounding and practical effectiveness enhance its significance.

Visual Insights

#

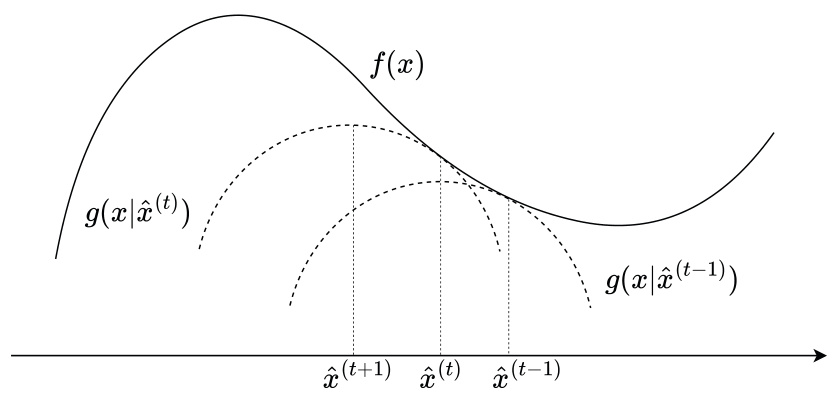
This figure shows the convergence of the FPC algorithm in terms of the NCut objective value for two UCI datasets: ‘Balloons’ and ‘Shuttle’. The x-axis represents the iteration number, and the y-axis represents the NCut objective value. The plots show that the FPC algorithm converges to the global optimum within a few iterations for both datasets. This demonstrates the algorithm’s efficiency and effectiveness in minimizing the NCut objective.

This table lists eight datasets used in the experiments, specifying the number of data points (N), the number of clusters (K), and the number of features for each dataset. The source of each dataset is also indicated.

In-depth insights

#

Multi-ratio FP

#

The heading “Multi-ratio FP” suggests an extension of fractional programming (FP) techniques to handle problems involving multiple ratios simultaneously. Standard FP methods often focus on single-ratio optimization, such as the classic Dinkelbach’s method. However, many real-world applications, particularly in areas like clustering (as evidenced by the paper’s focus on Normalized Cuts), present themselves as multi-ratio problems. This necessitates a more general and powerful framework. The proposed “Multi-ratio FP” likely introduces novel transformations or algorithms to efficiently solve these complex optimization problems. This could involve iterative schemes, perhaps leveraging techniques like minorization-maximization (MM) to iteratively refine solutions by optimizing individual ratios while considering their interplay. A key challenge is ensuring convergence to a globally optimal or near-optimal solution in the presence of multiple, potentially interacting, ratio terms. The effectiveness of such a framework is heavily dependent on its ability to efficiently handle the increased computational complexity and ensure robustness against local optima. The paper’s success would hinge on demonstrating a significant advantage over traditional FP approaches and other existing methods for solving multi-ratio problems in the chosen application domain.

NCut Optimization

#

The Normalized Cut (NCut) problem is a fundamental challenge in unsupervised clustering, aiming to partition data points into groups that minimize inter-cluster similarity while maximizing intra-cluster similarity. The optimization is computationally complex, often falling into the NP-hard category, making exact solutions intractable for large datasets. Many NCut algorithms rely on approximations, such as spectral clustering techniques, which tackle an eigendecomposition problem related to the graph Laplacian. However, these methods typically offer no performance guarantees and can be sensitive to parameter choices. Recent research explores fractional programming (FP) approaches, which offer a potentially more direct way to handle the ratio-based nature of the NCut objective. FP-based methods offer the possibility of deriving novel algorithms with improved convergence properties and solutions closer to the true optimal NCut; however, many existing FP techniques are limited to simpler cases and struggle with the multi-ratio, combinatorial nature of NCut. Therefore, advanced FP formulations, including those with multidimensional quadratic transforms, are being developed to address these limitations. Ultimately, the key to improving NCut optimization lies in finding better approximations that retain accuracy while achieving computational tractability, with fractional programming showing considerable promise in this arena.

FPC Algorithm

#

The Fractional Programming-based Clustering (FPC) algorithm, a novel approach to solving the Normalized Cut (NCut) problem, offers a unique perspective on multidimensional fractional programming. Its core innovation lies in efficiently handling multiple ratios simultaneously, unlike traditional methods. This is achieved by leveraging a multidimensional quadratic transform, which converts the NP-hard NCut problem into a bipartite matching problem solvable iteratively. The algorithm’s iterative nature, optimizing auxiliary variables alongside the clustering assignment, guarantees convergence towards a solution. While the core method assumes a positive semi-definite similarity matrix, an extension addresses indefinite matrices, broadening applicability. FPC demonstrates superior performance against existing NCut solvers, achieving lower objective values and improved clustering metrics across various datasets. A key advantage is the inherent efficiency, showcasing competitive running time comparable to spectral clustering, but with enhanced accuracy and stability. However, future work might explore the algorithm’s behavior under different similarity metrics and investigate strategies to further reduce computational complexity for extremely large datasets.

Experimental Results

#

The experimental results section of a research paper is crucial for validating the claims made and demonstrating the effectiveness of the proposed method. A strong experimental section should present results with clarity and precision, utilizing appropriate metrics and statistical analysis. Robustness checks, such as using various datasets or hyperparameters, are vital to demonstrate the generalizability of the findings and address potential limitations. A comparison to existing state-of-the-art methods, using identical evaluation criteria and datasets, is also essential to provide a fair assessment and highlight the proposed method’s improvements and advantages. Detailed descriptions of the experimental setup, including datasets, evaluation protocols, and implementation details are necessary for reproducibility. Visualizations, such as graphs and charts, can help in effectively presenting complex information. Clearly stating the limitations and potential biases of the experimental design further strengthens the credibility of the research. Finally, discussing the implications of the findings and suggesting areas for future work is a great way to conclude this important section.

Future Work

#

The ‘Future Work’ section of this research paper could explore several promising avenues. Extending the multidimensional FP method to handle indefinite similarity matrices more robustly is crucial, as the current approach relies on a positive semi-definite assumption. Investigating alternative factorization techniques for the numerator term in the multidimensional quadratic transform could improve efficiency and broaden applicability. Exploring the theoretical connections between the proposed FPC algorithm and other graph-based clustering methods, particularly spectral clustering, would provide deeper insights into its performance and limitations. Empirical evaluations on a wider range of datasets with varying characteristics (e.g., high dimensionality, noise levels, cluster shapes) would strengthen the claims of the paper. Finally, investigating the potential for parallelization or distributed computation to improve the scalability of the FPC algorithm for extremely large datasets is essential for practical applications.

More visual insights

#

More on figures

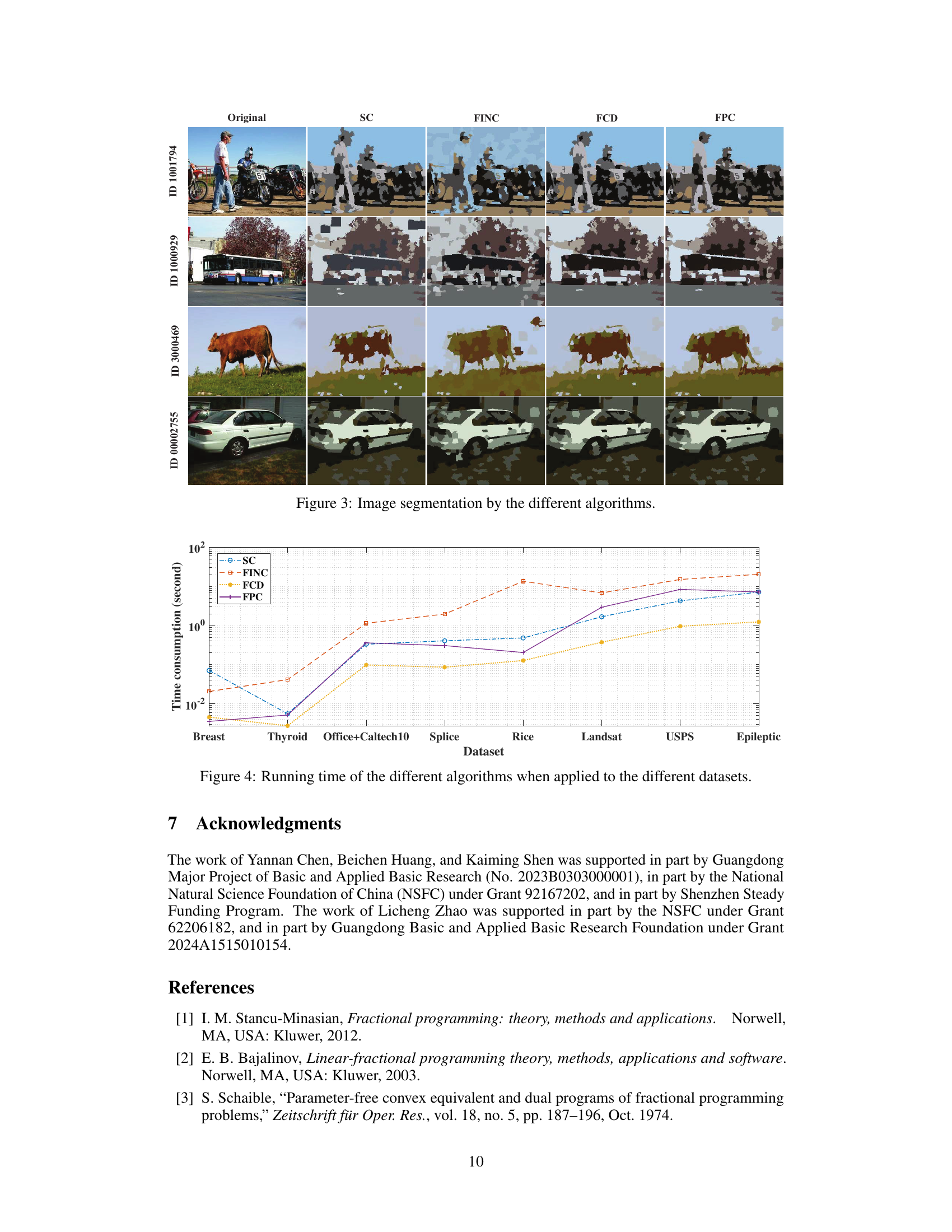
This figure shows the image segmentation results of different algorithms including the original image, SC, FINC, FCD and FPC on four different images. Each row represents a different image, and each column represents a different algorithm. It visually compares the performance of each algorithm in segmenting various images with complex backgrounds and shapes.

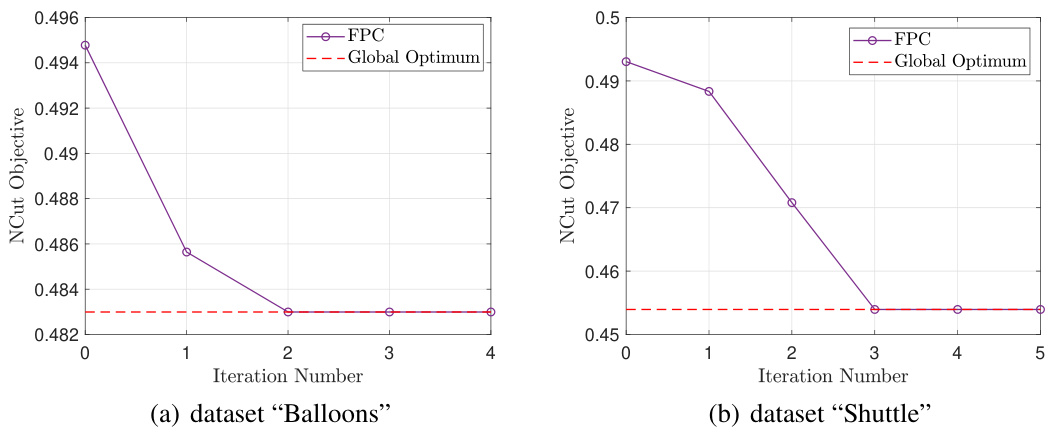
This figure shows the running time of four different graph clustering algorithms (SC, FINC, FCD, and FPC) across eight different datasets. The datasets vary in size and complexity, allowing for a comparison of algorithm efficiency under different conditions. The y-axis represents the time taken in seconds, and the x-axis displays the names of the datasets. The graph highlights the relative performance of each algorithm across these datasets.

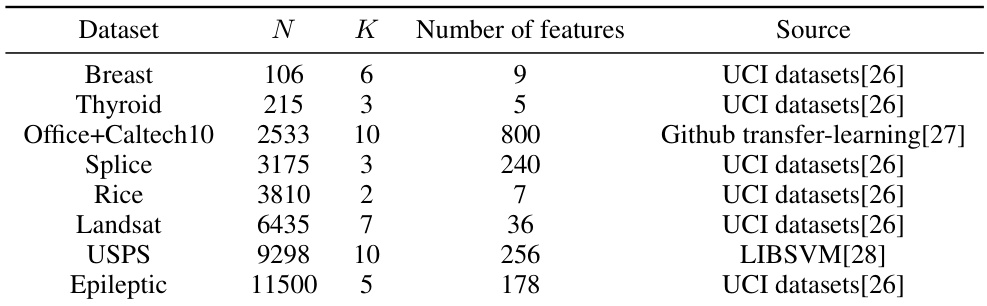
This figure illustrates the monotonic convergence property of the MM (Minorization-Maximization) method. The MM method iteratively approximates a difficult optimization problem by maximizing a surrogate function. The surrogate function, g(x|x^(t-1)), is designed to be less complex than the original objective function, f(x), and always below or equal to it. Each iteration finds the maximum of the surrogate function given the previous iteration’s solution. The figure shows that the original objective function value, f(x), is non-decreasing after each iteration of the MM method.

More on tables

This table lists eight datasets used in the paper’s experiments to evaluate the performance of the proposed fractional programming-based clustering (FPC) algorithm. For each dataset, it shows the number of data points (N), the number of clusters (K), the number of features for each data point, and the source of the dataset. The datasets vary significantly in size and characteristics, allowing for a comprehensive evaluation of the algorithm’s robustness.

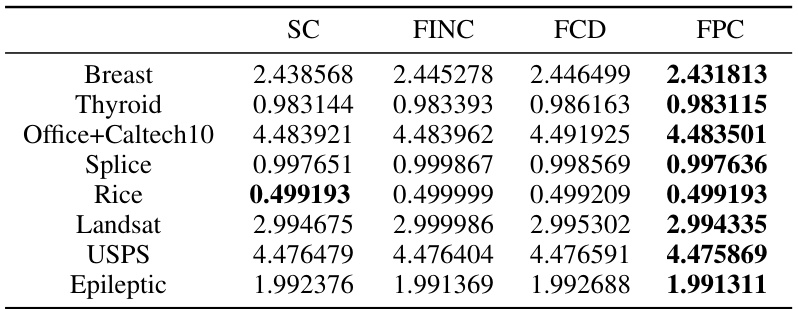
This table presents the results of four different algorithms (SC, FINC, FCD, and FPC) on eight datasets. Each algorithm attempts to minimize the normalized cut (NCut) objective function. The table shows the NCut values obtained by each algorithm for each dataset with random initialization. Lower values indicate better performance in minimizing the NCut.

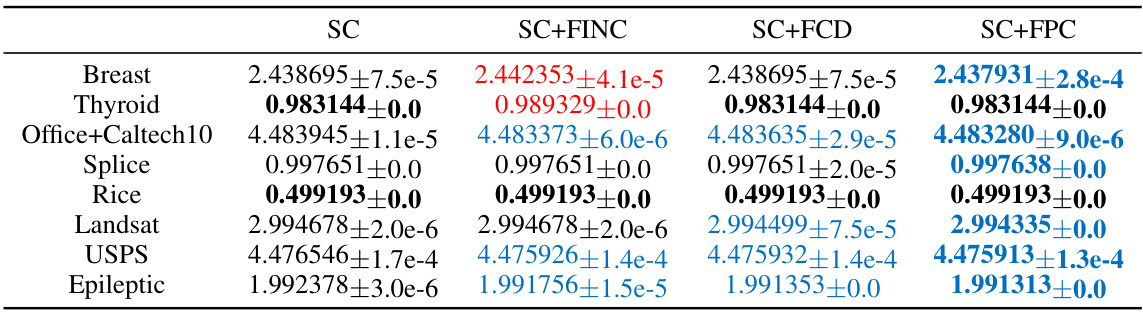
This table presents the NCut objective values obtained by four different algorithms (SC, SC+FINC, SC+FCD, and SC+FPC) when initialized using the SC algorithm. The results are shown for eight different datasets, each with its own number of data points and features. The values are accompanied by their standard deviations. Blue coloring indicates improvement while red indicates degradation compared to the SC baseline.

This table presents a comparison of four different clustering algorithms (SC, FINC, FCD, and FPC) across eight datasets. The performance of each algorithm is evaluated using three metrics: Accuracy (ACC), Normalized Mutual Information (NMI), and Adjusted Rand Index (ARI). Higher values for ACC, NMI, and ARI indicate better clustering performance. The table allows for a detailed assessment of the relative strengths and weaknesses of each algorithm in various clustering scenarios.

Full paper

#