Improving the Learning Capability of Small-size Image Restoration Network by Deep Fourier Shifting

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it introduces a novel Deep Fourier Shifting operator for image restoration, addressing the limitations of existing spatial shift operators. This offers a more efficient and robust approach to enhancing small-size image restoration networks, opening avenues for improved performance on resource-constrained devices and advancing low-level image processing. The information-lossless Fourier cycling method is a significant contribution with wide-ranging applications.

Visual Insights

#

This figure compares the spatial shift operator with the proposed Deep Fourier Shifting operator. The spatial shift operator moves each channel of the input tensor in a distinct direction, causing information loss and conflicting with image restoration requirements. In contrast, Deep Fourier Shifting is an information-lossless operator designed for image restoration, achieving a more stable performance gain with varying shift displacements and basic units across image denoising tasks. The graphs show PSNR (peak signal-to-noise ratio) performance for different shift configurations.

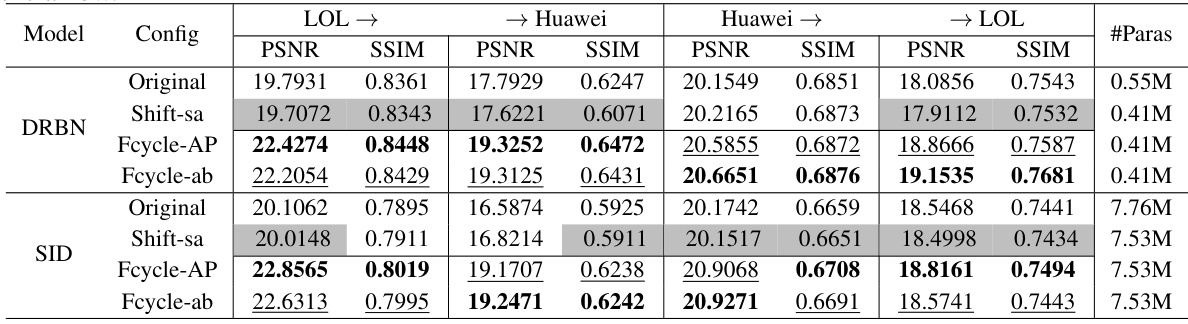
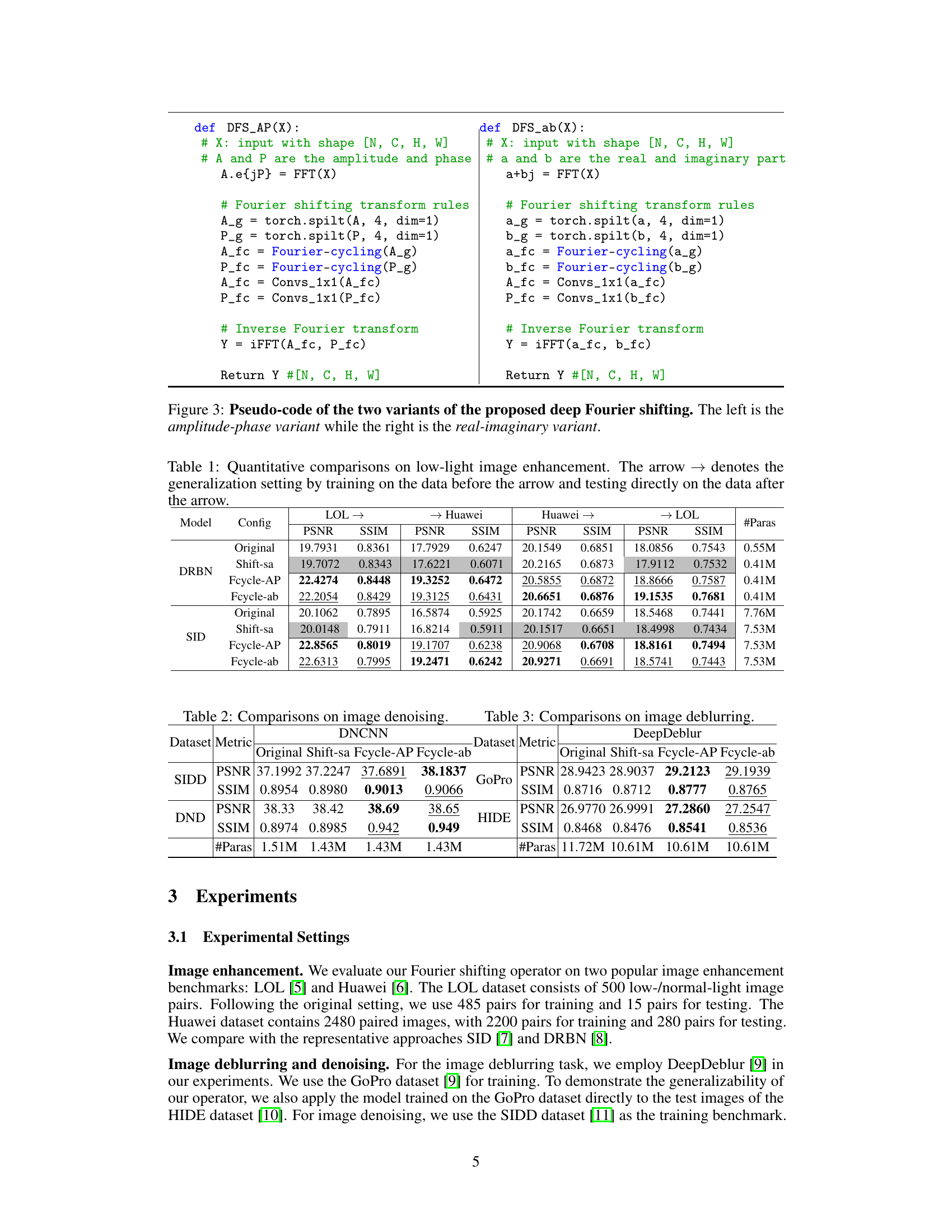
This table presents a quantitative comparison of different models’ performance on low-light image enhancement tasks. The models are compared using PSNR and SSIM metrics on two datasets (LOL and Huawei). The arrow ‘→’ indicates the generalization setting, where a model trained on one subset of the data is tested on another subset to evaluate its generalization ability. The table shows the performance of the original models, models using spatial shifting, and models using the proposed Deep Fourier Shifting (amplitude-phase and real-imaginary variants). The number of parameters (#Paras) for each model is also provided.

In-depth insights

#

Fourier Shift’s Power

#

The concept of “Fourier Shift’s Power” in image processing centers around leveraging the Fourier transform’s ability to represent signals in the frequency domain. Shifting in the frequency domain is computationally efficient and corresponds to a phase shift in the spatial domain. This offers significant advantages over traditional spatial-domain shifting methods for image restoration. Deep Fourier Shifting, a key innovation, capitalizes on the Fourier transform’s inherent periodicity by implementing information-lossless ‘Fourier cycling’. This strategy avoids the common pitfall of information loss associated with spatial shifting, making it particularly effective for image restoration tasks sensitive to spatial distortions. The amplitude-phase and real-imaginary variants of Deep Fourier Shifting offer flexibility, and their integration into existing networks as drop-in replacements for convolution layers demonstrates the practical applicability and efficiency of this approach. The results highlight superior performance gains across diverse image restoration tasks while maintaining computational efficiency. The method’s robustness is further underscored by consistent improvement across varying shift displacements, reinforcing its potential for real-world applications.

Lossless Shift Design

#

The concept of a “Lossless Shift Design” in image processing aims to address the limitations of traditional spatial shift operators, which suffer from information loss due to zero-padding. A key innovation is operating in the Fourier domain, where shifting becomes a cyclical permutation, thus preserving all original information. This lossless property is crucial for image restoration tasks, which are highly sensitive to information loss. Deep Fourier Shifting leverages this principle, designing variants that operate on amplitude-phase or real-imaginary components of the Fourier transform. These variants are computationally efficient and can be directly integrated into existing architectures, showing consistent performance improvements across various low-level vision tasks, demonstrating the effectiveness and potential of the lossless shift design in image restoration.

Image Restoration

#

Image restoration, a crucial aspect of computer vision, focuses on recovering a clean image from a degraded one. Techniques vary widely, encompassing methods like denoising, deblurring, and super-resolution. The field is constantly evolving, with deep learning methods achieving remarkable success in recent years. Deep Fourier Shifting, as discussed in the provided research paper, offers a novel approach. By cleverly leveraging the properties of Fourier transforms, it aims to improve the performance of smaller, more efficient restoration networks. This is particularly significant for resource-constrained applications, such as mobile devices. The method’s information-lossless cycling approach appears promising, though thorough testing and comparisons with existing state-of-the-art techniques are necessary to fully assess its efficacy and potential impact on the field.

Ablation Study

#

An ablation study systematically removes components of a model to assess their individual contributions. Its primary goal is to understand the impact of each part, isolating the effects and avoiding confounding factors. In the context of image restoration, an ablation study might involve removing or altering specific modules (e.g., Deep Fourier Shifting variants), comparing performance metrics to establish their importance. Well-designed ablation studies carefully control variables, ensuring that only one component changes at a time. The results provide evidence supporting the design choices made by the authors and help identify areas for improvement or potential redundancies. This method enhances the interpretability of the model, highlighting what aspects are crucial for achieving optimal performance and clarifying the reasons behind performance gains or losses. By analyzing how the model degrades as components are removed, ablation studies offer valuable insights into the model’s architecture and its underlying mechanisms.

Future Works

#

Future work could explore several promising avenues. Extending Deep Fourier Shifting to other modalities beyond image restoration, such as video processing or medical imaging, is a key area. Investigating the impact of different Fourier cycling strategies and exploring more sophisticated variations of the operator would enhance its flexibility. A comprehensive analysis of the operator’s theoretical properties and its relationship to other shift operators would deepen our understanding. Furthermore, empirical studies on various datasets and network architectures are crucial to validate the operator’s robustness and efficiency. Finally, applications in resource-constrained environments, leveraging the inherent computational efficiency of Deep Fourier Shifting, are worth investigating. This would enable wider accessibility and deployment of the method in real-world applications.

More visual insights

#

More on figures

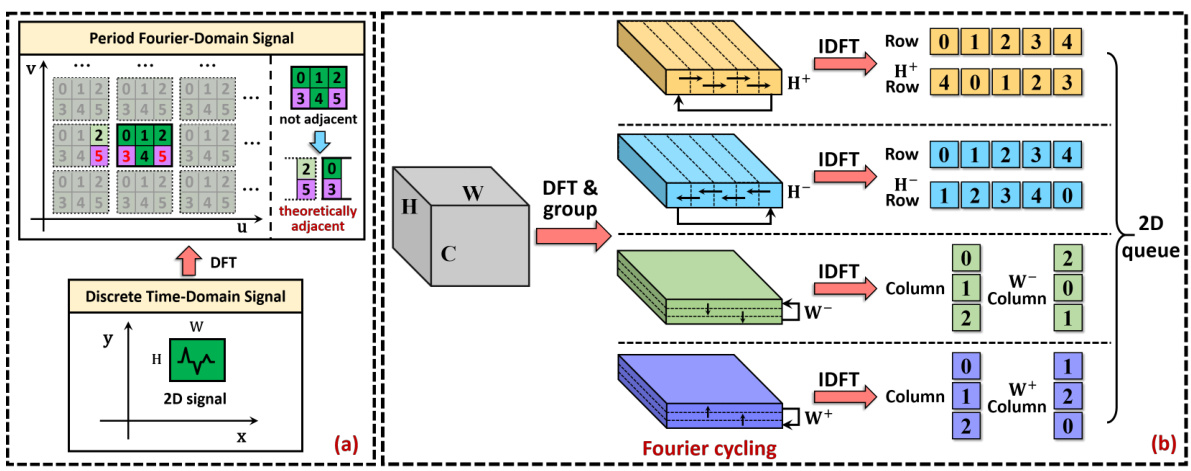
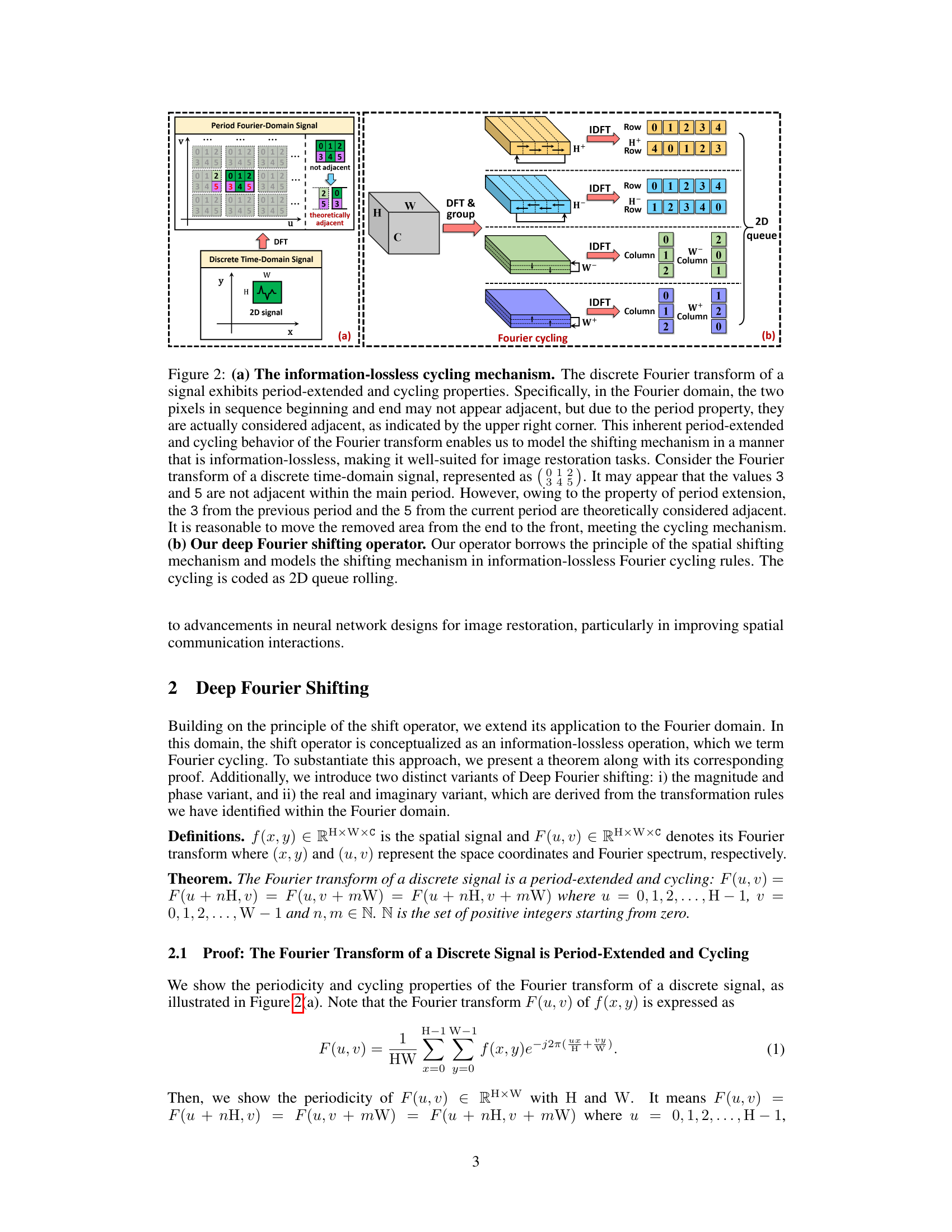
This figure illustrates the information-lossless cycling mechanism used in Deep Fourier Shifting. Panel (a) shows how the periodic nature of the Fourier transform allows for a shift operation without information loss by conceptually connecting the beginning and end of the signal. Panel (b) depicts the 2D queue rolling operation that implements the information-lossless Fourier cycling in the proposed Deep Fourier Shifting operator.

This figure shows the pseudo-code for the two variants of Deep Fourier Shifting: amplitude-phase and real-imaginary. Both variants start by applying a Fast Fourier Transform (FFT) to the input image. The amplitude-phase variant then separates the amplitude and phase components, applies Fourier cycling, and uses 1x1 convolutions before an inverse FFT. The real-imaginary variant performs a similar process but operates directly on the real and imaginary parts of the FFT output.

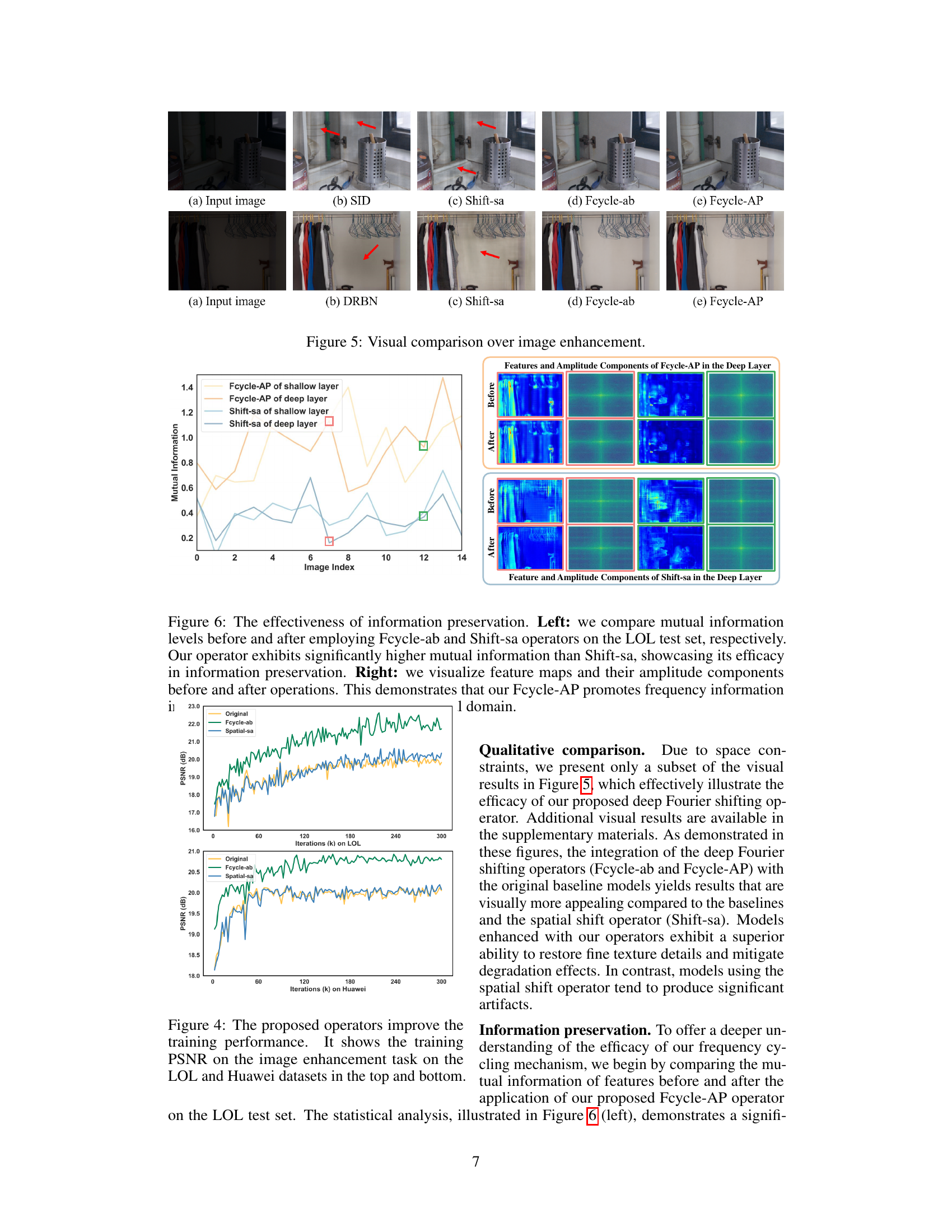
This figure shows a visual comparison of image enhancement results using different methods. The top row presents results for low-light image enhancement, comparing the input image with results from SID, Shift-sa, Fcycle-ab, and Fcycle-AP. The bottom row shows similar results for another low-light image enhancement method, DRBN, and the other three comparison methods. Red arrows in some images highlight specific areas where differences between the methods are more pronounced. Overall, the image shows the enhancement effects across different methods, illustrating the visual impact and differences between the proposed Deep Fourier Shifting method and the other methods.

This figure demonstrates the effectiveness of the proposed Deep Fourier Shifting in preserving information. The left panel compares the mutual information before and after applying the Fcycle-ab and Shift-sa operators on the LOL test set. The results show that the Deep Fourier Shifting method maintains significantly higher mutual information compared to Shift-sa, highlighting its effectiveness in information preservation. The right panel provides a visual comparison of feature maps and amplitude components before and after applying Fcycle-AP and Shift-sa to the deep layer. The visualization shows that Fcycle-AP promotes frequency information better than Shift-sa.

This figure shows the training performance of the proposed Deep Fourier Shifting (DFS) operators compared to the baseline and spatial shift operator on the LOL and Huawei datasets for image enhancement. The top graph shows the PSNR on the LOL dataset, while the bottom graph shows the PSNR on the Huawei dataset. The x-axis represents the number of training iterations, and the y-axis represents the PSNR. The figure demonstrates that both DFS variants consistently outperform the baseline and spatial shift operator throughout the training process.

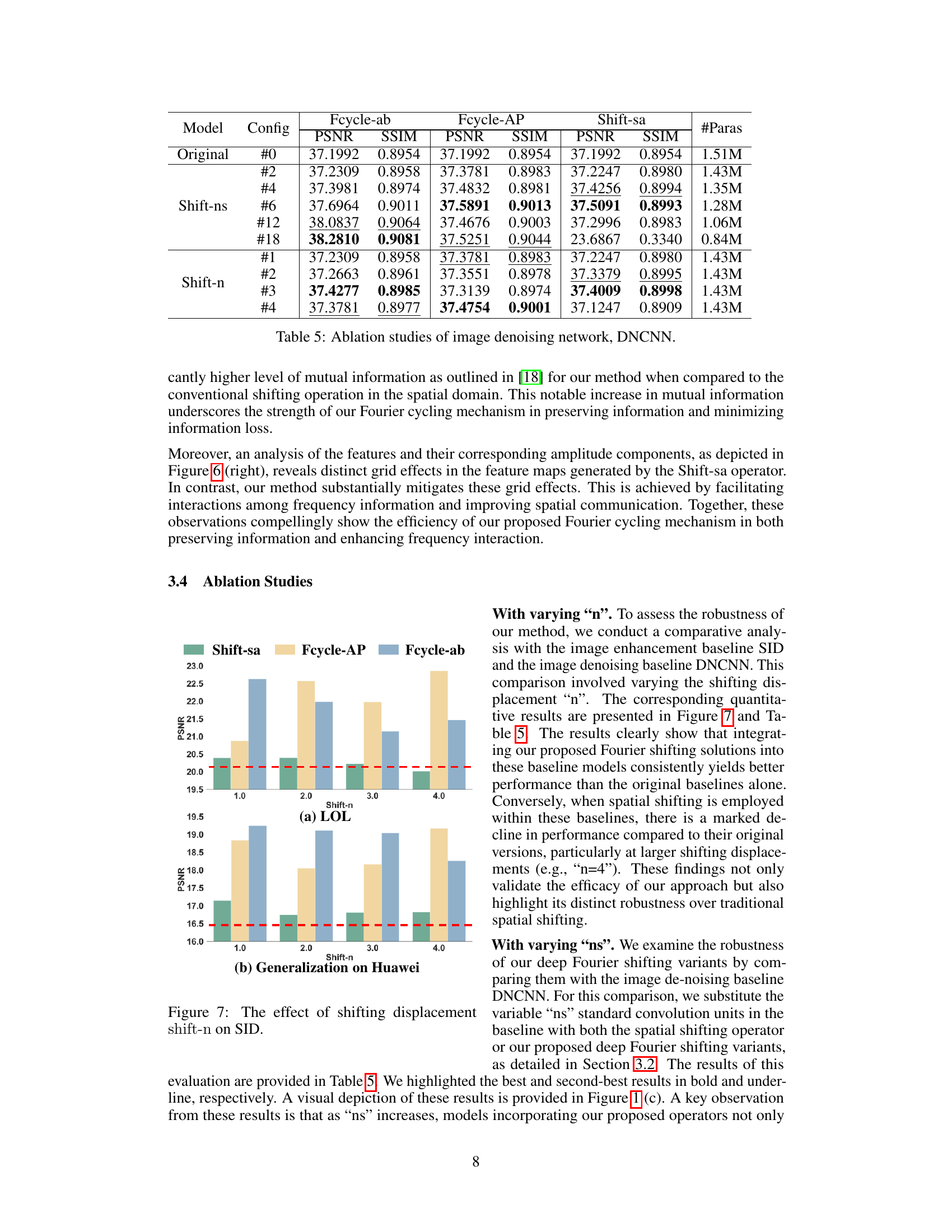
This figure visualizes the ablation study on the impact of varying the shifting displacement (n) on the performance of the proposed Deep Fourier Shifting. The results are shown for two datasets: LOL (a) and Huawei (b). The plots display the PSNR for three approaches: Shift-sa (baseline spatial shift), Fcycle-AP (amplitude-phase variant of Deep Fourier Shifting), and Fcycle-ab (real-imaginary variant). The dashed red line shows the original model’s performance without shifting. The graphs illustrate how the performance changes with different shift values (n=1, 2, 3, 4). The goal is to show that the proposed Deep Fourier Shifting (both variants) is more robust to changes in the shift displacement than the baseline spatial shifting.

More on tables

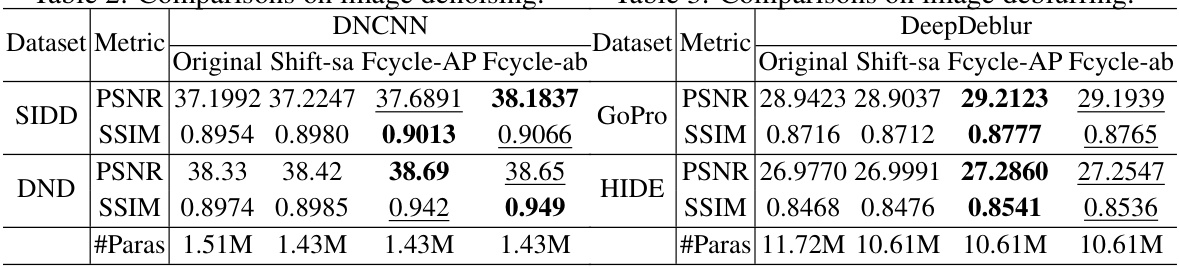
This table presents a quantitative comparison of the proposed Deep Fourier Shifting methods (Fcycle-AP and Fcycle-ab) against a baseline model (Original) and a spatial shifting method (Shift-sa) on image denoising tasks. The evaluation metrics used are PSNR and SSIM. Two datasets, SIDD and DND, are used for evaluation. The number of parameters (#Paras) for each model is also provided.

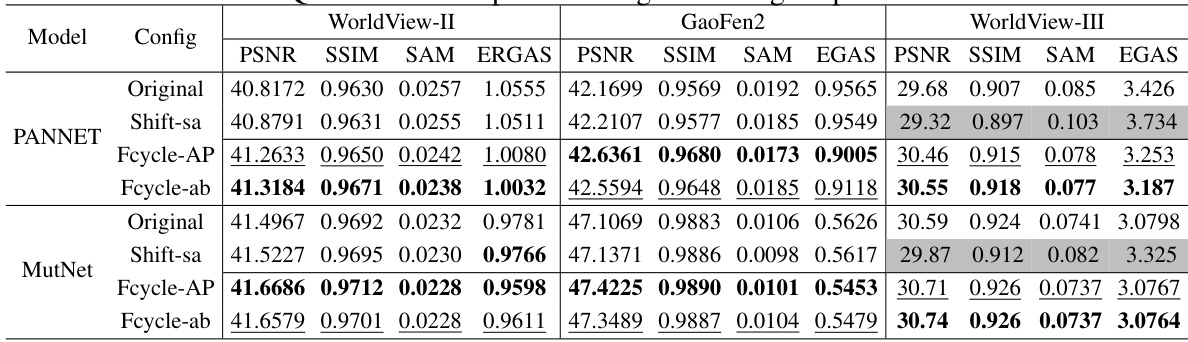
This table presents a quantitative comparison of different methods for guided image super-resolution using three metrics (PSNR, SSIM, SAM) and one evaluation criterion (ERGAS) on three different datasets (WorldView-II, GaoFen2, WorldView-III). The methods compared include the original method, the spatial shifting method, and two variants of the proposed deep Fourier shifting method (amplitude-phase and real-imaginary variants). The table shows that the deep Fourier shifting methods generally outperform the original methods and spatial shifting, indicating their effectiveness in enhancing guided image super-resolution performance.

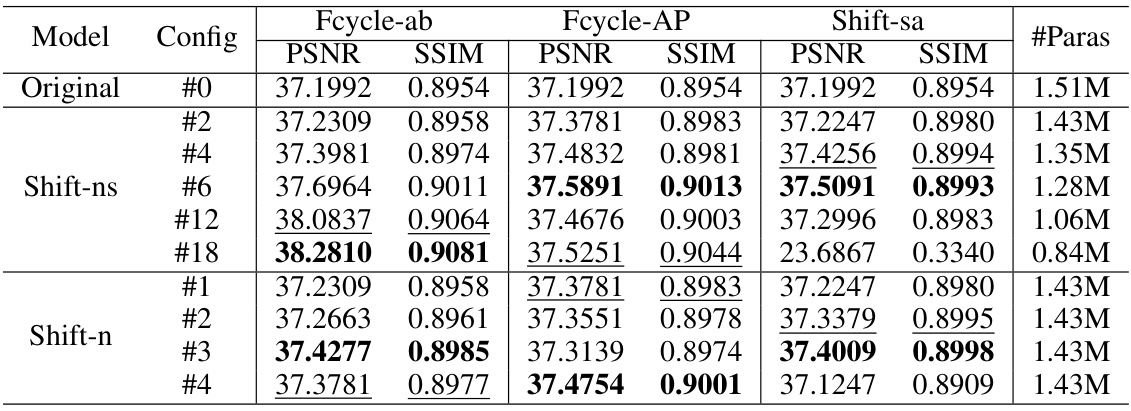
This table presents the ablation study results for the image denoising task using the DNCNN network. It shows a comparison of PSNR and SSIM values across various configurations, namely the original model and models with different variants of Deep Fourier Shifting (Fcycle-ab, Fcycle-AP) and spatial shifting (Shift-sa). The impact of varying shift displacement (’n’ and ’ns’) is also analyzed. The goal is to demonstrate the effectiveness and robustness of Deep Fourier Shifting in enhancing performance while maintaining or reducing model parameters compared to baseline and spatial shifting methods.

Full paper

#