HyperPrism: An Adaptive Non-linear Aggregation Framework for Distributed Machine Learning over Non-IID Data and Time-varying Communication Links

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in distributed machine learning due to its novel approach to handling non-IID data and time-varying links. HyperPrism’s adaptive non-linear aggregation offers a significant improvement over traditional linear methods, paving the way for more robust and efficient DML systems. The theoretical analysis and extensive experiments provide a strong foundation for future research in this area.

Visual Insights

#

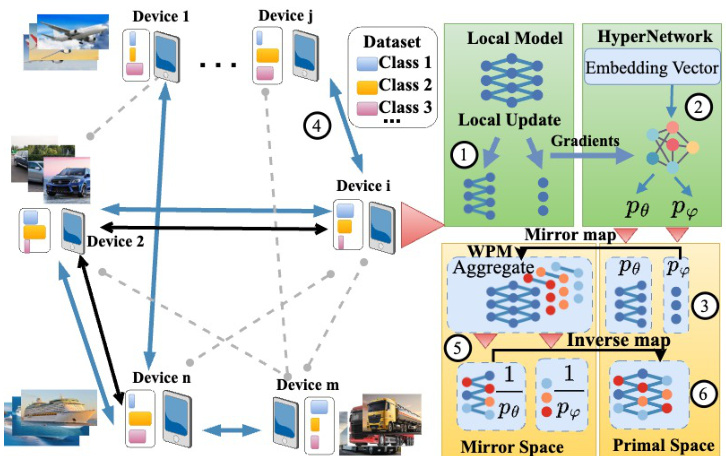
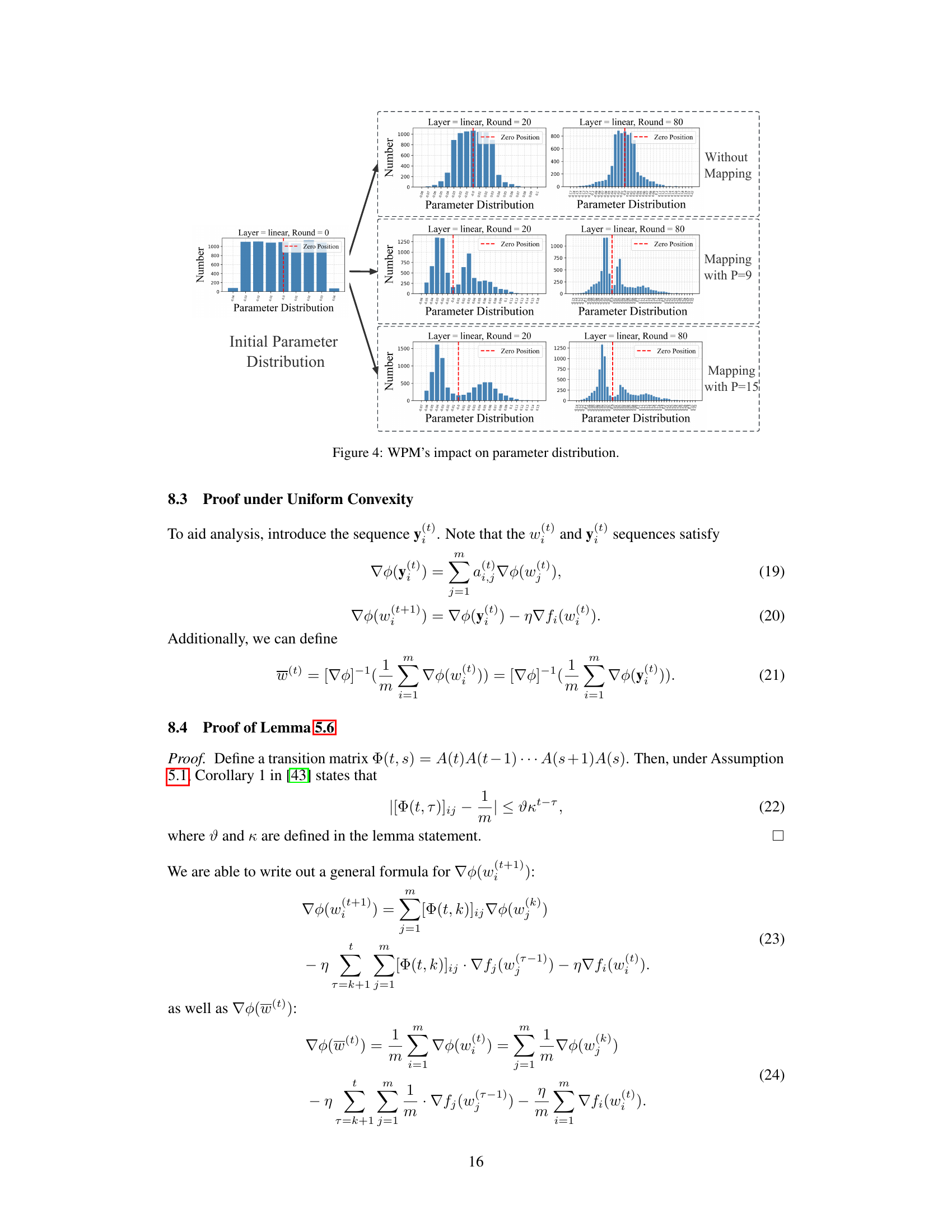
This figure illustrates the HyperPrism framework’s workflow. Each device performs local updates on its dataset (1), generates adaptive power degrees for model layers using hypernetworks (2), maps the model to a mirror space (3), exchanges models with neighbors (4), aggregates models using WPM in mirror space (5), and finally inverse maps the model back to the primal space (6).

This table compares the convergence rates of the HyperPrism framework with those of other methods from related works. The convergence rate is expressed in Big O notation, showing the dependence on parameters n (learning rate), p (power degree), m (number of devices), and T (number of rounds). The ‘Recovered’ column indicates whether the theoretical convergence rate is consistent with the empirical observations from prior studies.

In-depth insights

#

Adaptive DML

#

Adaptive Distributed Machine Learning (DML) tackles the challenges of heterogeneous data distributions and dynamic network conditions inherent in real-world deployments. Unlike traditional DML which relies on static algorithms and uniform data assumptions, adaptive DML employs techniques that dynamically adjust to the changing environment. This may involve adjusting model parameters based on data characteristics at individual nodes, adapting communication strategies to handle network failures or delays, or using non-linear aggregation methods to better reconcile model differences stemming from non-IID data. The key benefit of adaptive DML lies in its improved robustness and efficiency, enabling more reliable and scalable machine learning in decentralized systems. Adaptive algorithms are crucial to harness the full potential of distributed data while addressing the unique complexities of diverse environments.

Non-linear Aggreg.

#

The heading ‘Non-linear Aggreg.’ likely refers to a section detailing non-linear aggregation techniques in distributed machine learning. This is a significant departure from traditional linear methods (like averaging model parameters), which often struggle with the heterogeneity and divergence inherent in distributed settings. Non-linear aggregation strategies likely aim to address model divergence caused by non-IID data and time-varying communication links. The paper likely explores alternative aggregation functions, potentially including those based on geometric means, weighted power means, or more sophisticated mappings into a dual space. The advantages discussed might include faster convergence, improved accuracy, and enhanced robustness to noisy or unreliable communication. A critical aspect would be evaluating the computational cost of these non-linear methods to ensure they don’t outweigh the benefits in terms of overall training time and resource efficiency. The discussion could also include a comparison with existing linear aggregation techniques to highlight the strengths and limitations of the proposed non-linear approach.

HyperNetwork Tuning

#

HyperNetwork Tuning, in the context of distributed machine learning, presents a powerful mechanism to dynamically adapt model parameters across diverse devices. By employing hypernetworks, the system learns to generate optimal model weights based on device-specific embeddings and gradients. This adaptive approach addresses the challenges of non-IID data and time-varying communication by allowing each device to adjust its local model based on its unique data distribution and available connectivity. The technique offers a significant advancement over traditional linear aggregation methods because it enhances convergence speed and scalability while mitigating the impact of divergence forces in distributed settings. Automatic optimization of model parameters becomes feasible, leading to more efficient and robust distributed training, particularly crucial when handling diverse data and unpredictable network conditions.

Time-Vary Comm.

#

The section on ‘Time-Varying Comm.’ would explore the challenges and solutions related to dynamic communication networks in distributed machine learning (DML). It would likely discuss scenarios where the network topology changes over time, due to factors like node failures, mobility, or limited bandwidth. This poses a significant challenge as it affects the stability and convergence of algorithms relying on consistent communication patterns. The discussion would likely center on how to adapt DML algorithms to maintain performance even with intermittent connectivity and varying network delays. Strategies to address these issues may include techniques to handle message loss, efficient synchronization mechanisms, and robust aggregation algorithms resilient to inconsistent data flow. The effectiveness of different approaches, such as gossip protocols, or strategies that leverage local computation during communication disruptions, would likely be analyzed and compared. Overall, this section highlights the importance of designing resilient DML systems capable of effectively learning even under unstable communication conditions.

Non-IID Data

#

In distributed machine learning, Non-IID (non-independent and identically distributed) data poses a significant challenge. It arises when data points across different devices or nodes are not identically distributed, leading to model discrepancies and hindering the effectiveness of traditional aggregation methods. This heterogeneity stems from various factors such as differing user preferences, data collection biases, and device-specific characteristics. Addressing Non-IID data is crucial for ensuring model fairness and generalizability; otherwise, models may perform well on some devices but poorly on others. Consequently, strategies like personalized federated learning or robust aggregation techniques become necessary to account for the diverse data distributions.

More visual insights

#

More on figures

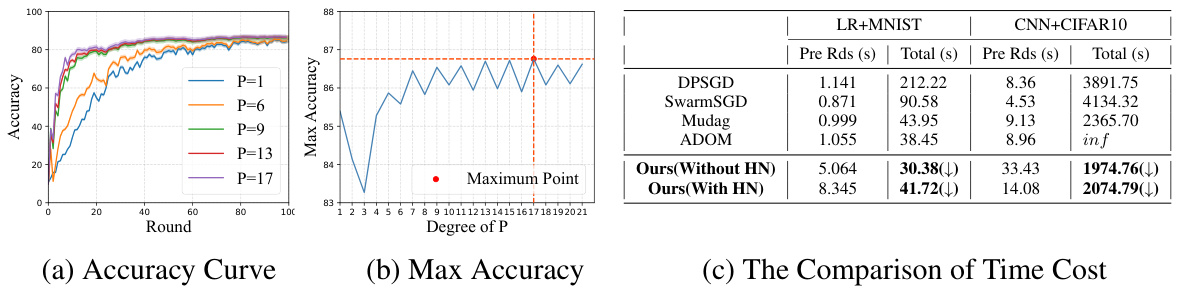
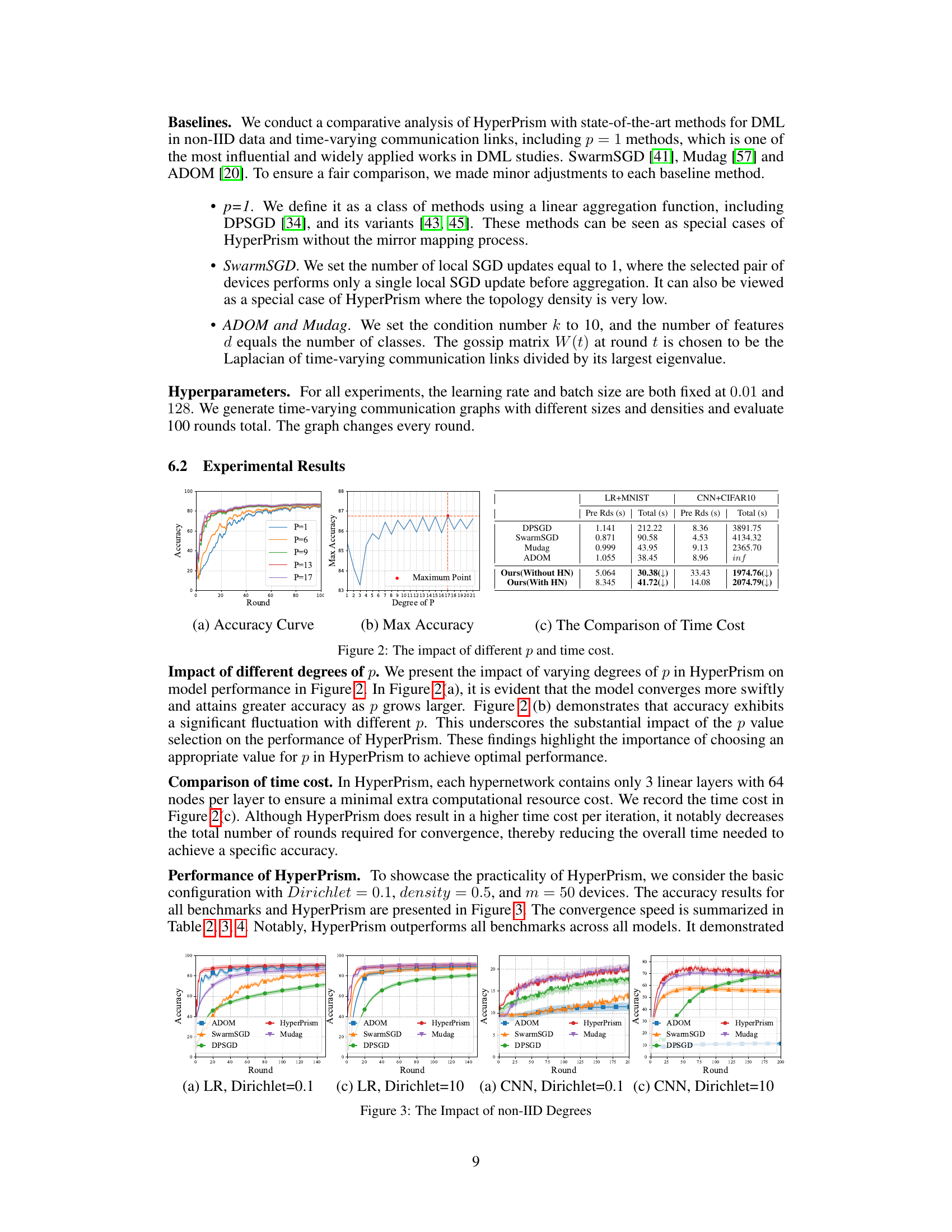
This figure shows the impact of different degrees of p on the model’s accuracy and the time cost. Subfigure (a) shows accuracy curves for different p values, demonstrating faster convergence with higher p. Subfigure (b) shows maximum accuracy achieved at different p values, indicating an optimal p exists. Subfigure (c) compares the time cost of HyperPrism with other baselines; while HyperPrism has a higher cost per round, the faster convergence leads to lower overall time to achieve a specific accuracy.

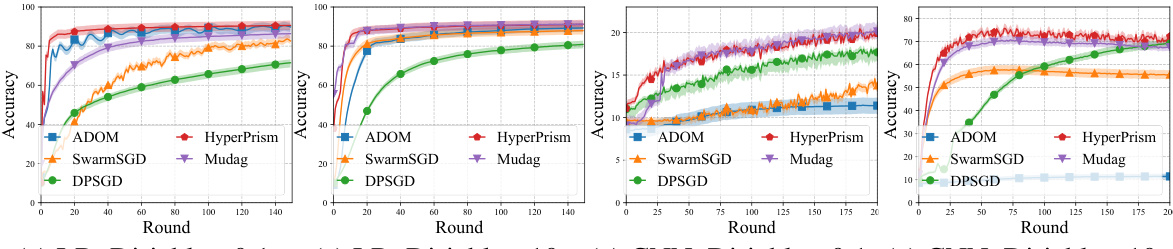
This figure displays the performance of HyperPrism and other baseline methods (ADOM, SwarmSGD, Mudag, DPSGD) under different non-IID data distributions (Dirichlet distributions with α = 0.1 and α = 10) for two different models (Logistic Regression with MNIST and CNN with CIFAR-10). The x-axis represents the training round, and the y-axis represents the accuracy. The shaded areas represent the standard deviation. The results demonstrate HyperPrism’s superior convergence speed and accuracy across various scenarios, especially in non-IID settings.

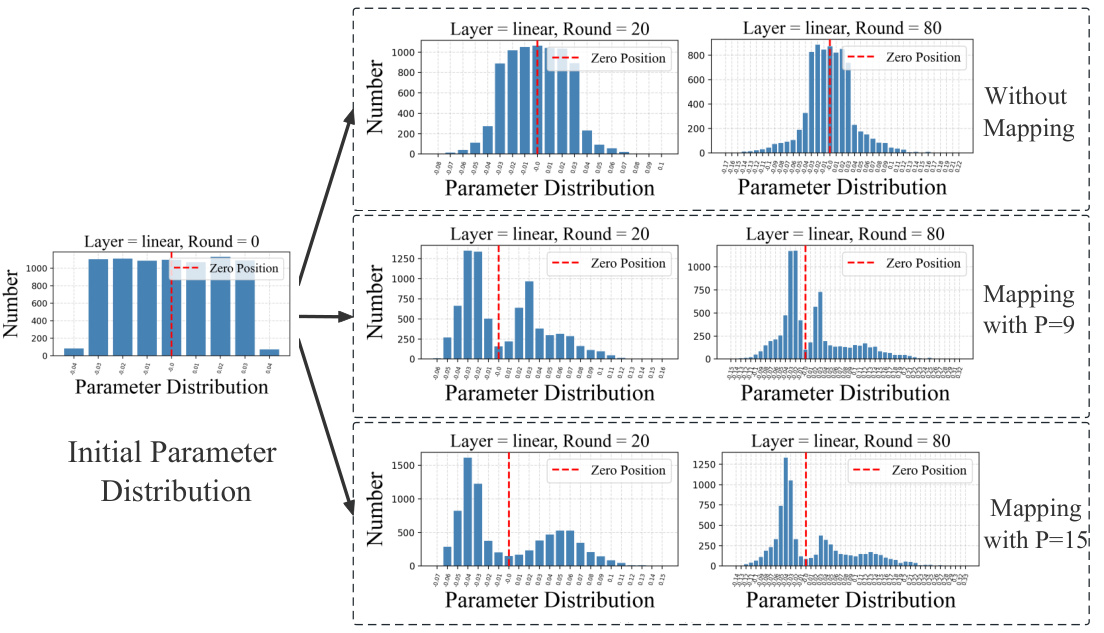
This figure illustrates the HyperPrism framework’s workflow. It begins with local model updates on each device’s dataset, followed by adaptive degree generation using hypernetworks. The models are then mapped to a mirror space, aggregated using Weighted Power Mean (WPM), and finally inverse-mapped back to the primal space. This process is iterative, with communication between neighboring devices at each step.

More on tables

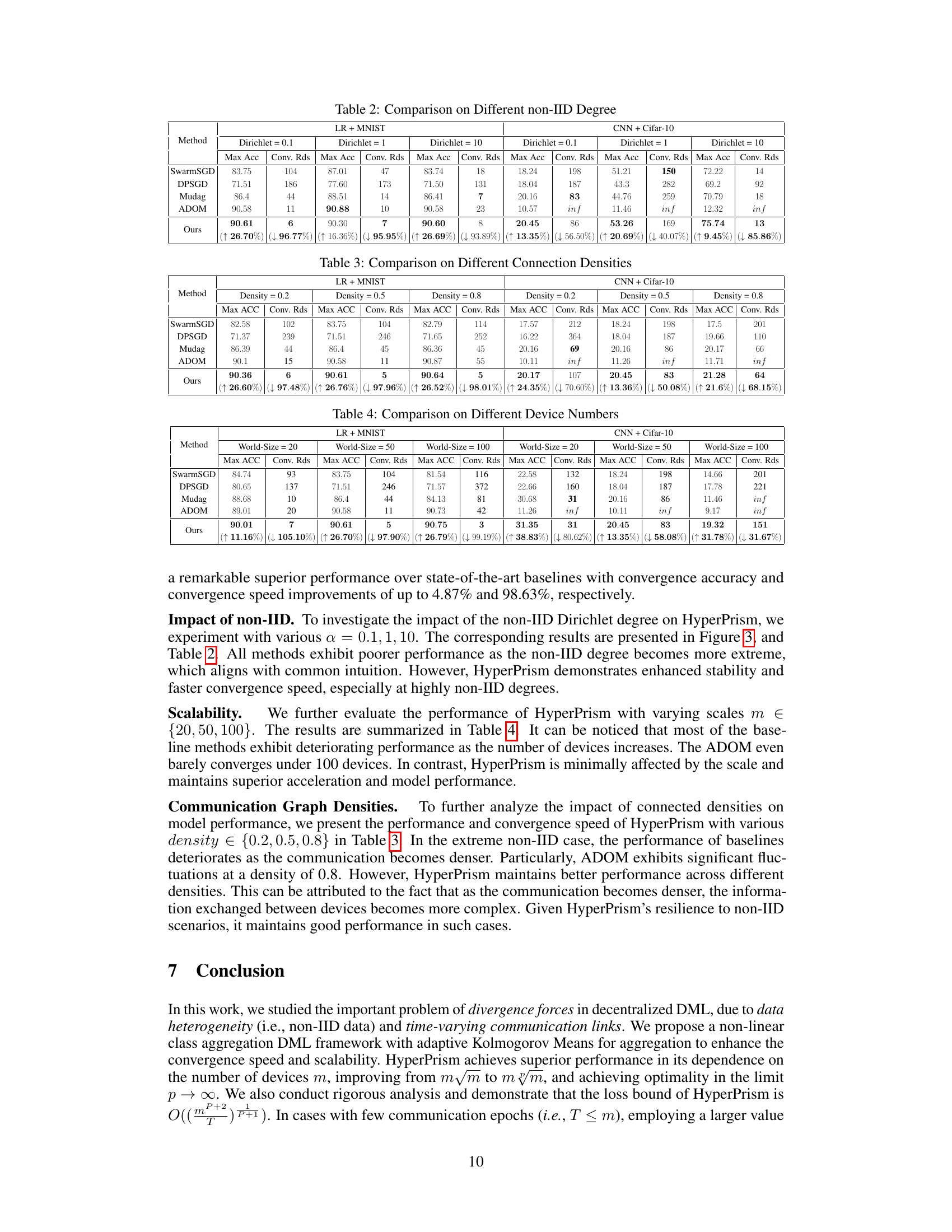
This table compares the performance of different algorithms (SwarmSGD, DPSGD, Mudag, ADOM, and the proposed HyperPrism) under varying degrees of non-IID data distribution (Dirichlet 0.1, 1, and 10). For each setting, it shows the maximum accuracy achieved and the number of convergence rounds for both Logistic Regression (LR) on MNIST and Convolutional Neural Network (CNN) on CIFAR-10. The results highlight the impact of data heterogeneity on the algorithms’ performance, demonstrating the effectiveness of HyperPrism in handling non-IID data.

This table presents the performance of various methods (SwarmSGD, DPSGD, Mudag, ADOM, and the proposed HyperPrism) under different communication densities (0.2, 0.5, and 0.8). The results are shown for both the Logistic Regression model on MNIST and the CNN model on CIFAR-10 datasets. The metrics reported include the maximum accuracy achieved and the number of convergence rounds required. The percentage change in performance compared to the baseline methods is also displayed for HyperPrism, illustrating its superior performance and robustness across varying connectivity conditions.

This table presents a comparison of the performance of various decentralized machine learning methods (including HyperPrism and baselines) across different numbers of devices (20, 50, and 100). It shows the maximum accuracy achieved and the number of convergence rounds for each method across two datasets (LR + MNIST and CNN + CIFAR-10) under non-IID data distributions. The results highlight the scalability and performance of each method as the number of devices increases. The last row shows the percentage improvement in accuracy and convergence rounds for HyperPrism compared to the baselines.

This table compares the convergence rates of different frameworks for distributed machine learning in terms of key parameters: n (learning rate), p (degree of power mean), m (number of devices), and T (number of rounds). It shows the theoretical convergence rates achieved by HyperPrism and several existing methods. The table is useful for understanding the relative scalability and efficiency of these frameworks under various conditions.

Full paper

#