Low Degree Hardness for Broadcasting on Trees

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper significantly advances our understanding of the computational complexity of inference problems, particularly in the context of broadcasting on trees. It provides a novel low-degree lower bound, demonstrating limitations of computationally efficient algorithms and establishing a connection to the information-theoretic Kesten-Stigum bound. This finding is crucial for algorithm design and the broader study of computational-to-statistical gaps, influencing research in areas like phylogenetic reconstruction, network analysis, and machine learning.

Visual Insights

#

This figure shows a binary rooted tree with depth 5. Several key concepts related to tree structure are illustrated using this example. Specifically, it shows the relationships between vertices using notation like ancestor, descendant, parent, child, and the height of a node.

In-depth insights

#

Low-Degree Hardness

#

The concept of “Low-Degree Hardness” in the context of the provided research paper likely explores the limitations of low-degree polynomial algorithms in solving specific computational problems. It suggests that certain inference tasks, particularly those involving complex probabilistic models like broadcasting on trees, may be inherently difficult for algorithms that rely on only low-degree polynomials to approximate solutions. This hardness result is significant because it suggests a computational-to-statistical gap, indicating that the problem’s inherent difficulty goes beyond simply the noise present in the data. The focus on low-degree polynomials is crucial due to their practical relevance in algorithm design; proving low-degree hardness provides stronger evidence of computational difficulty compared to other methods, and its implications for understanding the limits of certain algorithmic approaches are profound. The paper likely demonstrates that below a critical threshold (such as the Kesten-Stigum bound), low-degree polynomials fail to capture relevant information, even when information-theoretic methods succeed. This suggests that more sophisticated, potentially computationally intensive algorithms are needed for these types of problems.

Broadcasting on Trees

#

The concept of ‘Broadcasting on Trees’ in the context of this research paper likely refers to a communication process modeled on a tree-like graph structure. Information originates at the root node and propagates downwards through the branches to the leaf nodes. This process is often studied within the fields of statistical physics, computational biology (phylogenetic reconstruction), and algorithm design. The paper likely explores the computational complexity of inferring information about the root node, given observations at the leaf nodes. A key challenge is the trade-off between statistical efficiency (information-theoretic bounds) and computational efficiency (algorithmic complexity). The authors probably investigate the capabilities and limitations of low-degree polynomial algorithms in this inference task. Low-degree polynomials are used to analyze computational-to-statistical gaps in many inference problems, and this study may focus on whether low-degree polynomials suffice for efficient inference below the so-called Kesten-Stigum threshold, or if they are limited by the inherent complexity of the broadcasting process on trees.

Kesten-Stigum Bound

#

The Kesten-Stigum bound is a critical threshold in the study of reconstruction problems on trees. It marks the boundary between regimes where it is information-theoretically possible or impossible to recover the root state of a Markov chain given observations at the leaves. This bound is particularly relevant to broadcasting models on trees, where the root state propagates down to the leaves according to a Markov process. Above the Kesten-Stigum bound, efficient algorithms exist that can successfully reconstruct the root state. The computational complexity of this reconstruction below the bound remains an active area of research, with low-degree polynomial methods being extensively explored to potentially illuminate the computational-statistical gaps that might exist. Recent studies using the low-degree heuristic have advanced our understanding by proving lower bounds on the degree of polynomials needed for reconstruction below the bound. This highlights the inherent difficulty of these tasks and suggests the limitations of local algorithms in this domain. The Kesten-Stigum bound’s significance extends beyond theoretical analysis, with implications for practical applications such as phylogenetic reconstruction and community detection in networks.

Fractal Capacity

#

The concept of “Fractal Capacity” in the context of the research paper appears to be a novel metric designed to quantify the complexity of functions operating on the leaves of a tree. It leverages the recursive branching structure of the tree, breaking down complex functions into simpler components. The fractal capacity of a function is determined by the number of iterative steps required to decompose it into its most basic building blocks (singletons). This approach is particularly relevant because it captures the intricate relationships between leaf nodes and ultimately the root, which isn’t readily apparent in traditional metrics like the Efron-Stein degree. By focusing on fractal capacity, the authors likely aim to establish lower bounds on the computational complexity required to infer properties of the root, particularly in the challenging regime where the Kesten-Stigum bound is not tight. This fractal capacity metric might offer valuable insights into computationally hard inference problems on tree-structured data. This framework potentially allows for a more nuanced understanding of how local and global information propagates through the tree and influences the difficulty of inference.

Future Directions

#

Future research could explore generalizations beyond the specific Markov chain models used in this work. The low-degree hardness results established here offer a strong foundation for investigating the computational-statistical gap, but their extension to more complex models, such as those with non-homogeneous or non-stationary transitions, remains open. Another promising avenue would involve refining the low-degree bounds. The current bounds may not be tight and further work could lead to improvements, particularly for scenarios outside of the Kesten-Stigum bound. It would be interesting to see whether the low-degree hardness phenomenon persists with different tree structures. Exploring connections with other computational approaches, such as belief propagation and message passing algorithms, could lead to new insights and more efficient algorithms for inference in tree-based models. Finally, a deep dive into practical applications could potentially reveal the true implications and limitations of low-degree polynomials as a measure of computational complexity in settings beyond the theoretical framework presented here.

More visual insights

#

More on figures

The figure illustrates the notations used in the paper for representing vertices as words and for branch decomposition. The left side shows a tree with vertices labeled as words indicating their location in the tree. The right side focuses on a branch decomposition of a subset S of leaves, highlighting the parent p(S) and its children used for recursively decomposing S into smaller subsets (S₁, S₂, S₃). These subsets are then related to the fractal capacity concept.

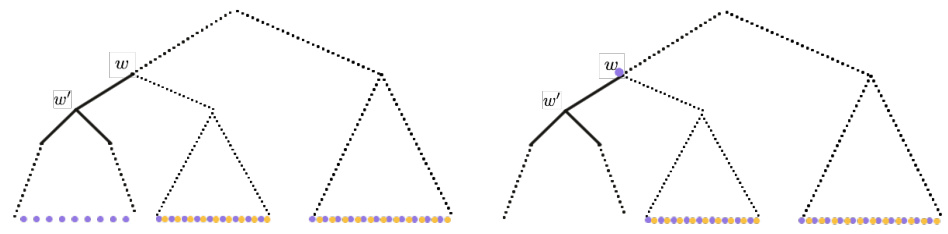
The figure demonstrates the conditional independence property of the Markov Random Field on a tree. The left panel shows two functions fa and fβ that depend on some variables. The right panel shows that conditioned on the values of variables in between fa and fβ, the two functions become independent, illustrating the Markov property.

This figure illustrates the conditional expectation. In the left panel, purple dots represent variables used in function fa and yellow dots represent variables used in function fβ. The right panel demonstrates that, given the Markov property, the conditional expectation E[fa(X)|Xw1] only considers variables within the subtree rooted at w1 and excludes variables from the subtree rooted at w2.

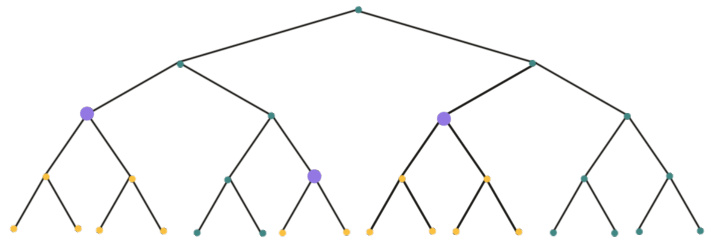
This figure shows a binary rooted tree with a depth of 5. It highlights key concepts used in the paper such as the definition of layers (the root is at layer 0, its children at layer 1, and so on), height of a node (the distance to the leaves), ancestor/descendant relationships, parent/child relationships, and kth-descendant/ancestor relationships. Node labels such as u, v, w, s, and t are used to illustrate these relationships.

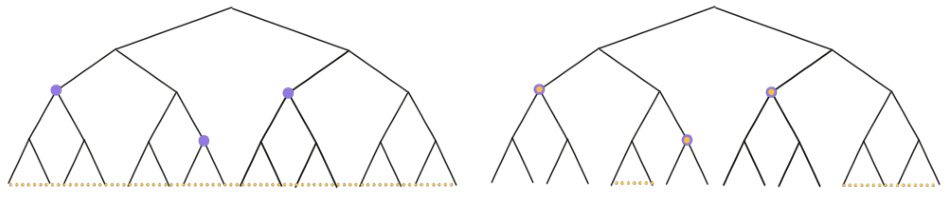
This figure illustrates the concept of bounding covariance in the context of broadcasting processes on trees. The left panel shows two functions, fa and fβ, whose inputs are represented by purple and yellow dots, respectively. These inputs are leaves of the tree. The right panel shows how, by conditioning on the values of variables (represented by yellow dots) above a certain point in the tree, the remaining input variables (purple dots) become less correlated, which allows for more effective analysis.

Full paper

#