↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Existing methods for training differentially private generative models often struggle with hyperparameter tuning and convergence due to noise injection in gradients or discriminator adaptation. These methods also face challenges in determining optimal training epochs due to trade-offs between privacy budget and convergence. This work proposes a novel approach that addresses these challenges by introducing a slicing privacy mechanism, which injects noise into low-dimensional projections of private data. This decoupled training process ensures strong privacy guarantees, while allowing for model-agnostic optimization and flexibility to adjust model architecture and hyperparameters.
The proposed method introduces a new information-theoretic measure, the smoothed-sliced f-divergence, and a kernel-based estimator for it. This estimator avoids adversarial training, which enhances convergence stability and robustness. The paper provides theoretical proofs for the privacy guarantees and the statistical consistency of the smoothed-sliced f-divergence. Extensive numerical experiments demonstrate that this approach produces synthetic data of higher quality compared to baselines, surpassing existing methods in various metrics.
Key Takeaways#
Why does it matter?#
This paper is important because it offers a novel approach to training generative models with differential privacy guarantees. It addresses the limitations of existing DP methods by decoupling the training process, enabling easier hyperparameter tuning, stable convergence, and improved data utility. This opens avenues for developing more efficient and effective privacy-preserving generative models, impacting various fields dealing with sensitive data. The introduction of a new information-theoretic measure, smoothed-sliced f-divergence, and its kernel-based estimator contributes to the broader field of DP algorithm development.
Visual Insights#
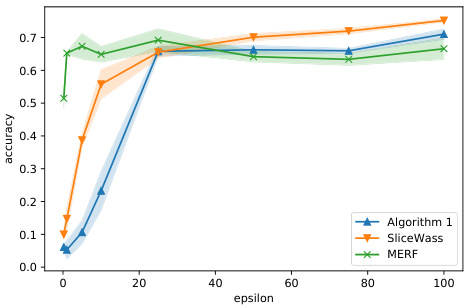
This figure shows the results of unsupervised domain adaptation experiments using the proposed method and the SliceWass baseline. The x-axis represents the privacy budget (epsilon), and the y-axis represents the accuracy of a classifier trained on synthetic data generated from a source domain (MNIST or USPS) and tested on the target domain (USPS or MNIST respectively). The figure demonstrates the performance of both algorithms across different privacy budgets and indicates that the proposed algorithm generally achieves higher accuracy.

The table compares the performance of different differentially private (DP) mechanisms for generating synthetic tabular data using the US Census data. Algorithm 1 is compared against SliceWass, DP-SGD, PATE, and MERF across five different tasks (Income, Coverage, Mobility, Employment, TravelTime), using various evaluation metrics. The results indicate the relative quality of synthetic data produced by different methods.
In-depth insights#
Slicing Privacy#
Slicing privacy, in the context of differential privacy for generative models, presents a novel approach to mitigating privacy risks during model training. Instead of injecting noise directly into gradients (as in traditional DP-SGD methods), it introduces noise into random low-dimensional projections of the private data. This clever strategy cleverly decouples the privacy-preserving step from the model training process. The method enjoys strong privacy guarantees because the noise is added to the projections before training begins. Consequently, subsequent training steps do not compromise privacy further. This decoupling offers substantial flexibility: hyperparameters can be easily tuned, architectures modified, and training epochs adjusted without incurring additional privacy costs, a significant advantage over gradient-based methods where such modifications necessitate re-injecting noise. The resulting noisy projections serve as the training data, enabling the generative model to learn the underlying data distribution without directly accessing sensitive information. The approach is also model-agnostic, making it broadly applicable to a wide variety of generative models. However, careful consideration must be given to the dimensionality of the projections, aiming to balance privacy guarantees against the utility of synthetic data. A too low dimension risks compromising data representation, while a too high dimension may not provide sufficient privacy amplification.
Smoothed Divergence#
The concept of “Smoothed Divergence” in a research paper likely involves modifying a standard divergence measure (like KL-divergence or Wasserstein distance) to improve its robustness and/or tractability. Smoothing might involve adding noise or using kernel density estimation to handle the challenges of estimating divergences from finite samples, especially in high dimensions. This smoothing is crucial for stability and reducing sensitivity to outliers, which are common issues when dealing with real-world data that may be noisy or incomplete. The paper may investigate the theoretical properties of the smoothed divergence, such as its consistency and convergence rates. Consistency would demonstrate that the smoothed divergence accurately reflects the true divergence between distributions as the sample size increases. The convergence rate would quantify how fast this convergence occurs. Furthermore, the paper would likely discuss the practical implications of the smoothed divergence. For instance, it might propose a new algorithm for training generative models or estimating density ratios, leveraging the improved properties of the smoothed divergence. A significant part of the paper’s analysis may focus on how the degree of smoothing affects the bias-variance trade-off; too much smoothing could introduce bias, masking important differences between distributions, while too little smoothing could result in high variance and unstable estimates. The overall goal is likely to propose a refined divergence measure that balances theoretical soundness with practical applicability, leading to more robust and efficient algorithms in machine learning and related fields.
Generative Training#
Generative training, in the context of differential privacy, presents a unique challenge: creating high-quality synthetic data while adhering to strict privacy constraints. Traditional methods often introduce noise directly into gradient updates, impacting model convergence and hyperparameter tuning. The core idea of decoupling the privacy-preserving step from the model training step is crucial. This allows for flexibility in model architecture, hyperparameter adjustments, and the number of training epochs without affecting the overall privacy guarantee. The introduction of novel information-theoretic measures, like the smoothed-sliced f-divergence, allows for statistically consistent training and provides strong privacy guarantees by carefully injecting noise into low-dimensional projections of the data. By sidestepping noisy gradients, this approach offers greater efficiency and improved data quality compared to traditional methods. The emphasis is on achieving a balance between privacy and utility, offering a significant advancement in the field of privacy-preserving generative model training.
DP Guarantees#
Differential Privacy (DP) guarantees are crucial for privacy-preserving machine learning. The paper likely establishes DP guarantees for a novel mechanism, possibly involving a slicing technique or a new method of noise addition. A key aspect would be the quantification of privacy loss using parameters like epsilon (ε) and delta (δ). Strong DP guarantees are essential, showing that the method limits the impact of individual data points on the output. The analysis may involve techniques like Rényi Differential Privacy (RDP) to simplify the composition theorem and provide tighter bounds. The choice of parameters (ε, δ) is critical, balancing privacy with utility. The paper should justify these choices, possibly demonstrating that they meet regulatory requirements or industry standards. The analysis should consider the effect of dataset size, dimensionality, and other hyperparameters on privacy. A rigorous proof is expected, demonstrating the correctness of the DP guarantees. Finally, the paper might show that the DP mechanism is composable, allowing the training process to be extended without compromising privacy.
Empirical Results#
An effective ‘Empirical Results’ section in a research paper should present a thorough evaluation of the proposed method, comparing its performance against relevant baselines across various metrics. Key aspects include clarity in describing the experimental setup (datasets, parameters, evaluation metrics), the use of appropriate statistical measures to assess significance, and a comprehensive discussion of the results. The discussion should not only highlight the strengths of the proposed method but also acknowledge any limitations or weaknesses, offering potential explanations and future directions. Visualizations like tables and graphs should be used effectively to present the results concisely and intuitively. A strong focus on reproducibility is vital; the section should provide sufficient details to allow others to replicate the experiments. Ultimately, a well-crafted ‘Empirical Results’ section enhances the paper’s credibility and impact by convincingly demonstrating the method’s effectiveness and robustness.
More visual insights#
More on tables
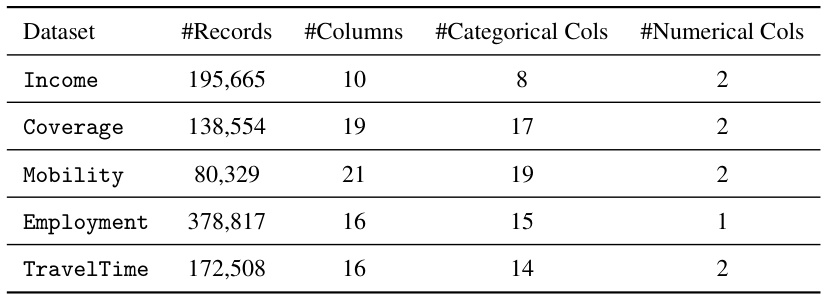
This table presents details of the five datasets used in the paper’s experiments. Each dataset includes a target column used for the LogitRegression evaluation metric. The table shows the number of records, the total number of columns, and the breakdown of columns into categorical and numerical features for each dataset.
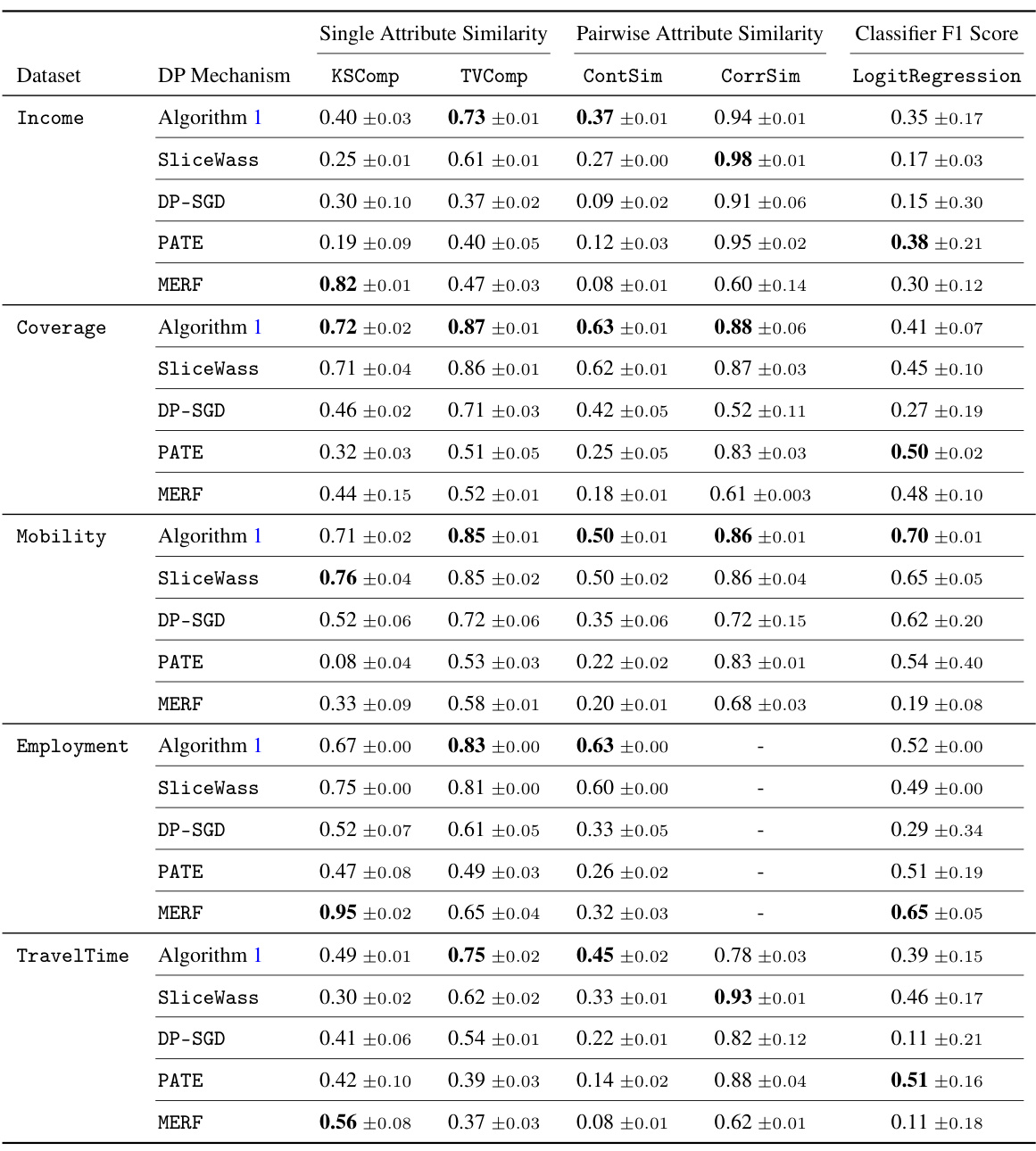
This table compares the performance of the proposed algorithm (Algorithm 1) against four baseline methods (SliceWass, DP-SGD, PATE, and MERF) for generating synthetic tabular data under a privacy budget of 5.1. The comparison uses five datasets from the US Census American Community Survey and several evaluation metrics assessing the similarity between the synthetic and real data distributions.
Full paper#