↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Decentralized machine learning is attractive due to its scalability and privacy-preserving nature but often suffers from high communication costs and slow convergence. Existing methods struggle to balance these factors, especially when dealing with diverse datasets distributed across multiple nodes. Many decentralized algorithms converge slowly because information mixing is inefficient, creating a trade-off between communication cost and speed.
This paper proposes the B-ary Tree Push-Pull (BTPP) algorithm. BTPP employs two B-ary spanning trees to distribute information efficiently. This approach minimizes communication since each agent only communicates with a small number of neighbors. Importantly, BTPP is theoretically proven to achieve linear speedup, converging much faster than existing decentralized methods. This improvement is particularly significant for smooth nonconvex and strongly convex objective functions, showing superior performance even on heterogeneous datasets.
Key Takeaways#
Why does it matter?#
This paper is important because it presents a provably efficient decentralized algorithm for distributed learning, a crucial aspect of modern machine learning. It addresses the challenges of communication overhead and slow convergence in existing decentralized methods, offering a novel solution with significantly improved performance. The B-ary Tree Push-Pull (BTPP) method and its theoretical analysis provide valuable insights and new avenues for future research in distributed optimization and machine learning.
Visual Insights#

This figure shows two spanning trees used in the B-ary Tree Push-Pull (BTPP) algorithm. Each tree has 10 nodes and a branching factor (B) of 2. The tree on the left (GR) represents the communication graph for distributing model parameters, where information flows from parent nodes to child nodes. The tree on the right (GC) is the inverse of the left tree, used for distributing stochastic gradients, with information flowing from child nodes to parent nodes. The root node (1) has a self-loop in GC. These trees form the basis of the BTPP algorithm’s communication structure.
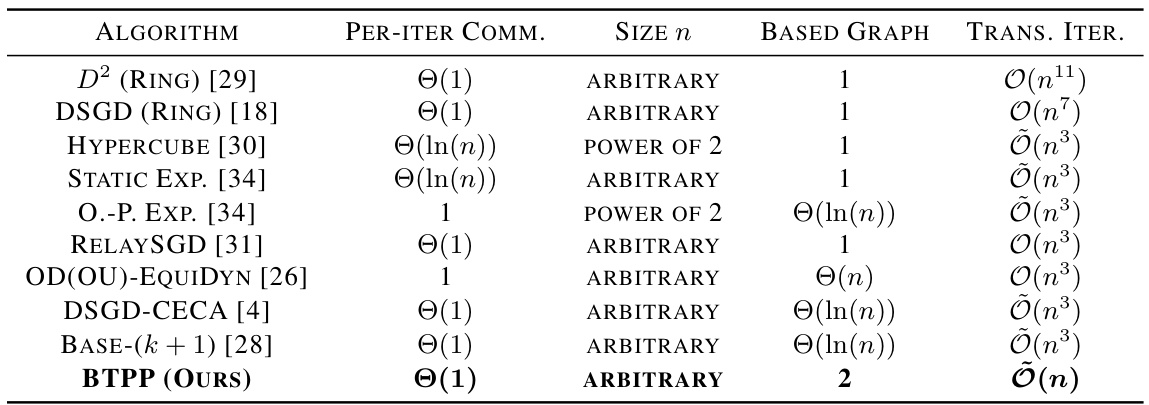
The table compares various distributed stochastic optimization algorithms under smooth non-convex objective functions. It shows the number of communications per iteration for each agent, the type of graph topology used, the number of graph topologies used across the entire process, and the number of transient iterations. The notation Õ(·) in the table hides polylogarithmic factors for easier readability.
In-depth insights#
BTPP Algorithm#
The BTPP algorithm, a decentralized stochastic gradient method, stands out for its provably efficient approach to distributed learning on heterogeneous data. Leveraging a B-ary tree topology, it distributes parameter updates and gradient information across the network, significantly reducing communication overhead. Each agent interacts with a limited number of neighbors (B+1), minimizing communication burden while ensuring efficient information dissemination. The theoretical analysis demonstrates linear speedup for both smooth non-convex and strongly convex objective functions, with significantly improved transient iterations compared to state-of-the-art methods. Two B-ary spanning trees are cleverly utilized to manage the push and pull operations for parameters and gradients, respectively, allowing for simultaneous updates. Furthermore, the algorithm’s inherent simplicity and adaptability to arbitrary network sizes makes it a promising solution for large-scale distributed machine learning tasks, particularly in scenarios with heterogeneous data distributions.
Convergence Analysis#
A rigorous convergence analysis is crucial for establishing the reliability and efficiency of any machine learning algorithm. The analysis should demonstrate that the algorithm converges to a solution, ideally with quantifiable bounds on the rate of convergence. For distributed learning algorithms, the analysis should also address how the communication topology and the heterogeneity of data across nodes impact convergence. Key aspects to explore are the algorithm’s transient phase, characterizing the initial period before the algorithm settles into its asymptotic behavior, and the impact of algorithm parameters, such as step size and batch size, on both the transient phase and the asymptotic convergence rate. A well-conducted analysis often involves mathematical tools to prove convergence bounds, considering various factors such as smoothness, strong convexity or non-convexity of the objective function, and noise characteristics of the gradient estimates. The results would ideally showcase linear speedup and a small transient phase, which are desirable properties for practical algorithms. Finally, numerical simulations should validate the theoretical findings and provide a practical demonstration of the algorithm’s convergence behavior.
Communication Tradeoffs#
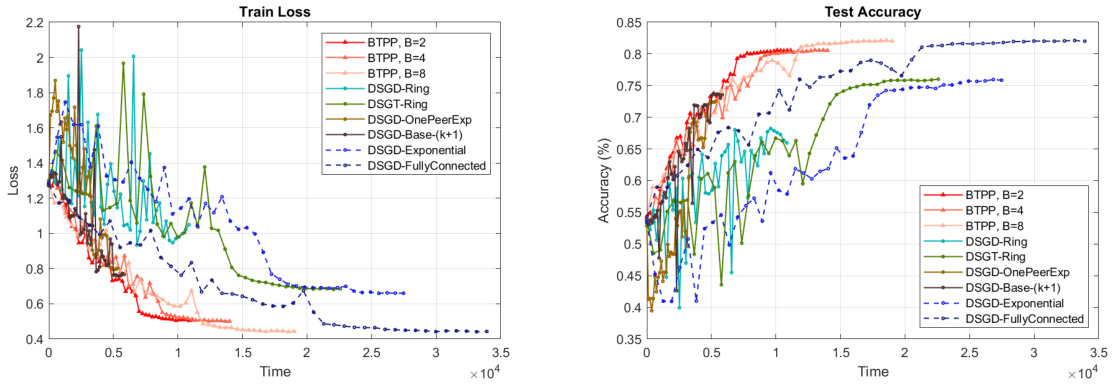
Communication tradeoffs in distributed learning represent a fundamental challenge: balancing the speed of convergence with the communication overhead. Faster convergence often necessitates frequent communication rounds between nodes, leading to increased network congestion and latency. Conversely, reducing communication may prolong the training process and potentially hinder the overall performance. Decentralized algorithms often attempt to optimize this balance, utilizing network topologies that minimize per-iteration communication while maximizing information dissemination across the network. Sparsity in communication graphs is one strategy to reduce overhead, but this can slow down convergence. The paper analyzes this tradeoff through a novel B-ary tree push-pull method, demonstrating that a carefully designed tree structure can achieve efficient communication and linear speedup for both smooth convex and nonconvex objectives.
Heterogeneous Data#
The concept of “Heterogeneous Data” in distributed learning is crucial because it acknowledges the realistic scenario where data isn’t uniformly distributed across participating agents. This heterogeneity poses challenges to traditional algorithms that assume homogeneous data distribution, leading to slower convergence and reduced efficiency. The paper addresses this by proposing a novel algorithm (BTPP) which leverages a B-ary tree structure to effectively manage and distribute information across the network. This structure ensures efficient communication even with non-uniform data distribution, allowing for faster convergence despite the presence of heterogeneous data. A key aspect of the BTPP is its consideration of the variance in data samples as well as its ability to deal with arbitrary topologies making it suitable for deployment in diverse and dynamic environments. The efficacy of BTPP in handling heterogeneous data highlights its practical relevance to real-world distributed learning scenarios.
Future Directions#
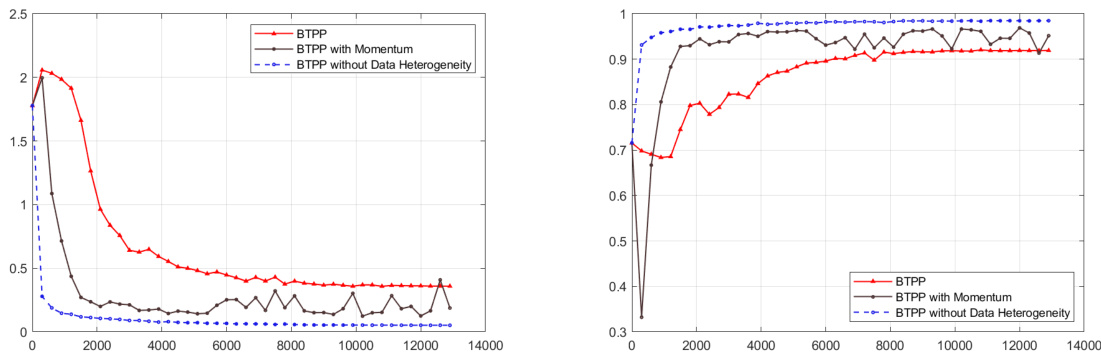
Future research directions stemming from this B-ary Tree Push-Pull (BTPP) method could explore adaptive strategies for selecting the branching factor (B). Currently, B is a hyperparameter; however, an adaptive mechanism that adjusts B based on network conditions or convergence rate could significantly enhance efficiency. Investigating BTPP’s robustness to various network topologies beyond the B-ary tree is crucial, particularly considering more complex and realistic network structures prevalent in distributed systems. The impact of heterogeneous data distributions and noisy gradients on BTPP’s convergence properties warrants further analysis. Further research could develop extensions of BTPP for handling decentralized optimization problems with constraints or non-smooth objective functions. Finally, a key area for future work is to evaluate BTPP’s performance on real-world, large-scale machine learning applications to demonstrate its practicality and scalability.
More visual insights#
More on figures

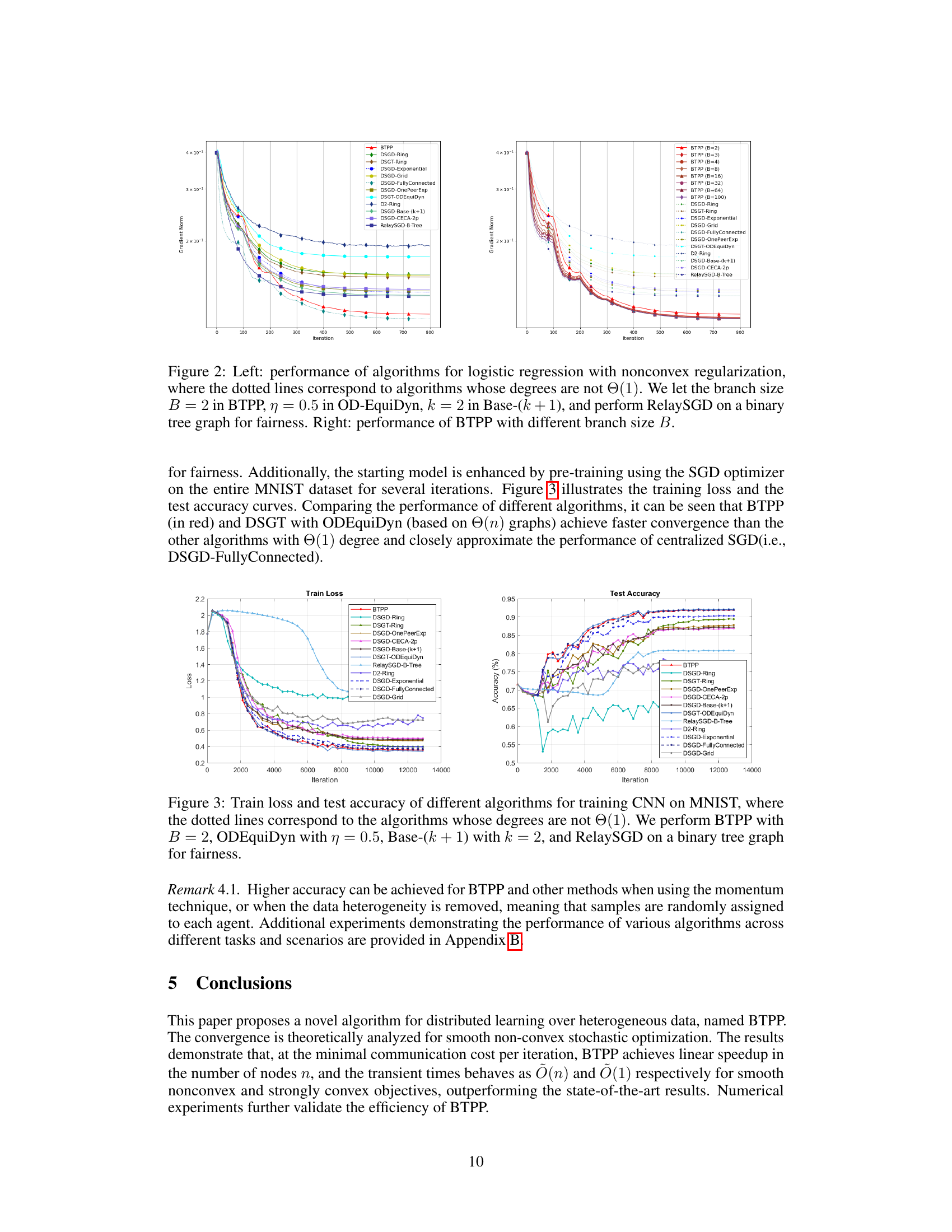
The left plot compares the performance of BTPP with other algorithms for logistic regression with non-convex regularization. The right plot shows how the performance of BTPP changes with different branch sizes (B).

The left panel compares the performance of BTPP against other algorithms for logistic regression with non-convex regularization. The right panel shows how the performance of BTPP changes with different branch sizes (B). Both plots use the gradient norm as a metric to assess convergence speed.

The left plot compares the performance of various algorithms for solving logistic regression with non-convex regularization. The y-axis represents gradient norm, and the x-axis represents the number of iterations. BTPP (in red) shows faster convergence than others with Θ(1) degree and closely approximates centralized SGD. The right plot illustrates how BTPP’s performance changes with different branch sizes (B). Increasing B improves convergence speed but increases communication cost per iteration.

This figure compares the performance of various decentralized optimization algorithms on a logistic regression task with non-convex regularization. The left panel shows the gradient norm over iterations for BTPP (with B=2) and other algorithms, highlighting BTPP’s faster convergence. The right panel demonstrates how BTPP’s performance improves with increasing branch size B, approaching that of centralized SGD. Different graph topologies are considered for each algorithm to ensure fair comparison.
The left plot compares various algorithms on a logistic regression task with non-convex regularization. BTPP (with B=2) is shown to converge faster than other algorithms that have a communication overhead of Θ(1) per iteration, achieving performance comparable to centralized SGD. The right plot shows how varying the branch size B in BTPP affects its convergence rate. Increasing B leads to faster convergence, but at the cost of increased communication per iteration.
The left plot compares the performance of BTPP with other algorithms on a logistic regression task with nonconvex regularization. The right plot shows how BTPP’s performance changes when varying the branch size B.
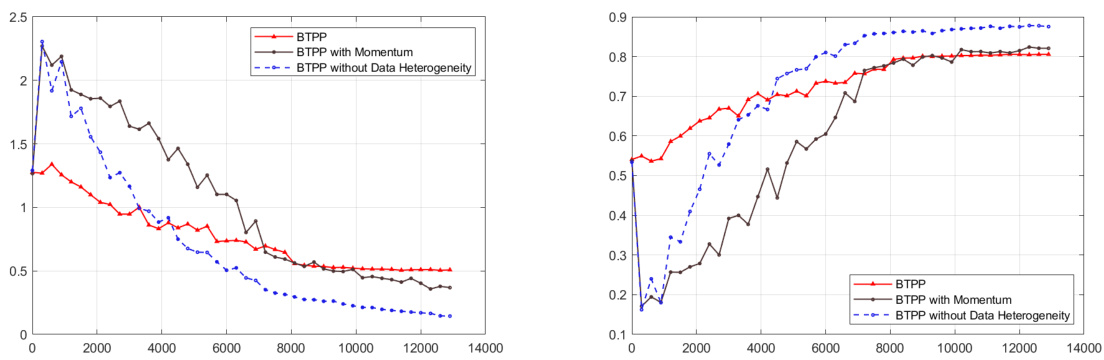
The left plot compares the performance of various algorithms on a logistic regression task with nonconvex regularization. The algorithms with a degree of Θ(1) (meaning each node communicates with at most one other node) show improved performance compared to those with higher degree. BTPP is highlighted for its performance. The right plot shows how the performance of BTPP changes with differing branch sizes (B). Increasing B improves performance, although also increasing computational cost per iteration.
Full paper#