↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
ReLU regression, a fundamental non-convex learning problem, poses significant challenges under differential privacy (DP) constraints, particularly in high-dimensional scenarios. Existing solutions often rely on strong assumptions about bounded data norms, which limit their applicability to real-world datasets. This limitation has motivated researchers to revisit the problem, leading to the development of improved approaches.
This paper introduces two novel DP algorithms, DP-GLMtron and DP-TAGLMtron. DP-GLMtron uses a perceptron-based approach with adaptive clipping and a Gaussian mechanism to enhance privacy. DP-TAGLMtron builds upon DP-GLMtron and further improves the privacy-utility trade-off by employing a tree aggregation protocol. Rigorous theoretical analysis demonstrates that these algorithms perform better than conventional methods like DPSGD, even with high-dimensional data and relaxed assumptions on data distribution. Empirical results validate these findings.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in differential privacy and machine learning. It addresses the challenges of applying differential privacy to non-convex models like ReLU regression, a common task in deep learning. The novel algorithms proposed offer better utility than existing methods, especially in high-dimensional settings, providing practical guidance for developing privacy-preserving machine learning systems. The analysis also extends beyond typical data assumptions, opening up new avenues for research in this rapidly evolving field.
Visual Insights#
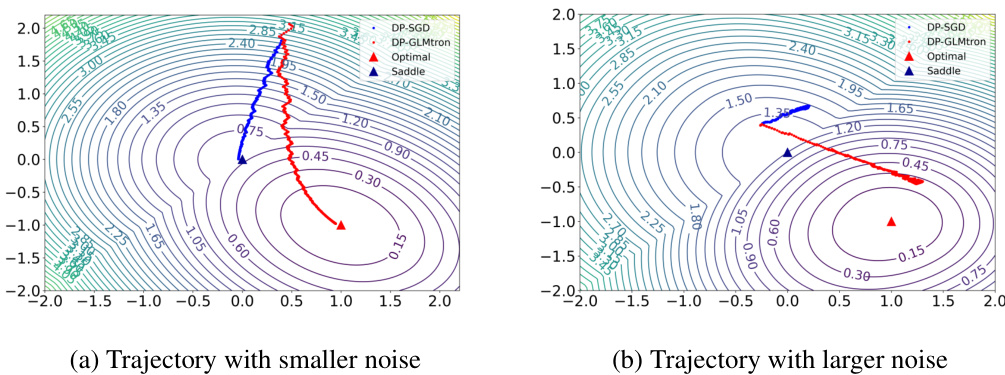
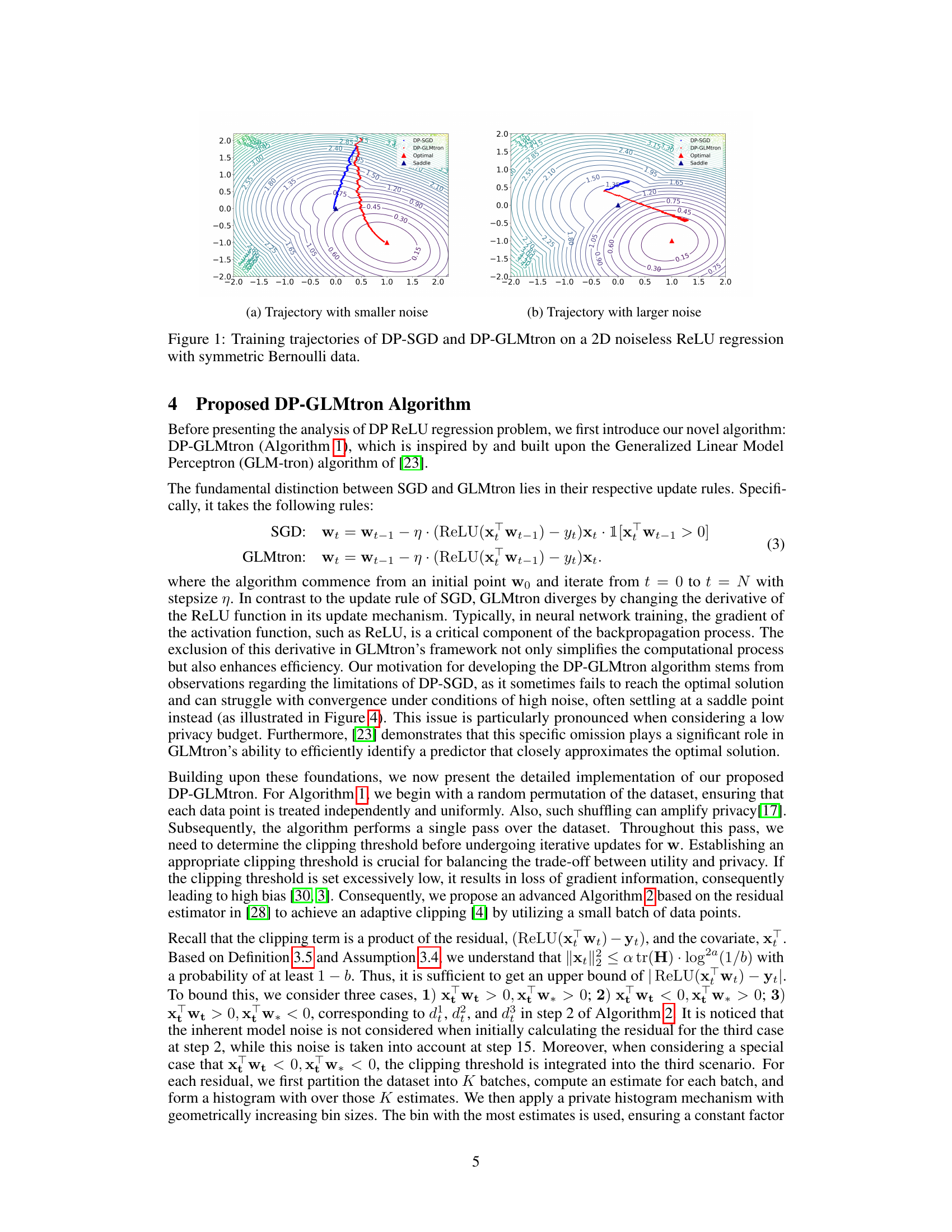
This figure displays the training trajectories of two differentially private algorithms, DP-SGD and DP-GLMtron, on a 2-dimensional ReLU regression problem with no added noise. The data points are generated from a symmetric Bernoulli distribution. Two subfigures are presented, each showing different levels of noise added during the training process. The trajectories illustrate the path taken by each algorithm towards convergence (or lack thereof). Red triangles mark the optimal solution, while blue triangles represent saddle points. The figure visually demonstrates how DP-GLMtron outperforms DP-SGD, particularly in higher noise scenarios, by avoiding saddle points and reaching the optimum.

This table compares the upper and lower bounds of the excess population risk for three different differentially private (DP) ReLU regression algorithms: DP-PGD, DP-GLMtron, and DP-TAGLMtron. It shows the privacy constraints and data assumptions for each method. The effective dimensions (Deff and Dpri) are highlighted as they are defined differently than in the traditional approach, offering a more nuanced comparison across different algorithms and data characteristics. Note that the effective dimensions do not rely directly on the dimension d.
In-depth insights#
DP-ReLU Revisted#
The study “DP-ReLU Revisited” makes significant contributions to the field of differentially private machine learning. It addresses the limitations of existing differentially private ReLU regression methods, particularly in high-dimensional settings. The authors introduce novel algorithms, DP-GLMtron and DP-TAGLMtron, which demonstrate improved performance compared to traditional methods like DP-SGD. A key focus is relaxing the stringent assumption of bounded data norms, allowing for broader applicability to real-world datasets. The theoretical analysis provides excess population risk bounds, revealing insights into how data distribution impacts learning in high dimensions. DP-TAGLMtron is especially significant as it addresses limitations of DP-GLMtron concerning small privacy budgets, achieving comparable performance with only a logarithmic increase in the utility upper bound. Overall, this research enhances our understanding and capabilities for privacy-preserving ReLU regression, especially in high-dimensional and overparameterized regimes.
Novel DP Algos#
The heading ‘Novel DP Algos’ suggests a discussion of new algorithms designed for differential privacy (DP). A thoughtful analysis would delve into the specifics of these algorithms, examining their mechanisms for adding noise to protect privacy while maintaining utility. Key aspects to consider include the type of noise added (e.g., Gaussian, Laplace), the method for calibrating noise to data sensitivity, and the theoretical guarantees provided regarding privacy and utility. The analysis should also evaluate the computational complexity and efficiency of the algorithms, and potentially compare them to existing DP methods. Particular attention should be paid to how the algorithms handle high-dimensional data or non-convex optimization problems, areas often posing challenges in DP. Finally, a discussion of the practical implications and potential limitations of the novel algorithms, along with any empirical evaluations or real-world applications, would significantly enhance the overall understanding of their contribution to the field of differential privacy.
Eigenvalue Impact#
The impact of eigenvalues on differentially private (DP) ReLU regression, especially in high-dimensional settings, is a crucial aspect of this research. Eigenvalues directly relate to the data covariance matrix, reflecting the distribution of feature importance. Traditional DP analyses often assume Gaussian-like data, simplifying the covariance to a scaled identity matrix, effectively ignoring eigenvalue decay. This paper challenges that assumption and demonstrates that eigenvalue decay significantly affects utility bounds. Algorithms such as DP-GLMtron and DP-TAGLMtron, which are developed in this paper, demonstrate improved utility by leveraging such decay, particularly in overparameterized regimes where the dimension exceeds the number of samples. Faster eigenvalue decay consistently leads to lower excess risk, indicating that the methods are less sensitive to the curse of dimensionality in such scenarios. The analysis in this paper highlights the importance of considering data distribution beyond simplistic Gaussian assumptions when designing and analyzing DP algorithms, thus offering valuable insights into the interplay between data characteristics and privacy-utility trade-offs.
High-Dim Analysis#
A high-dimensional analysis of differentially private (DP) mechanisms is crucial because the performance of DP algorithms often degrades significantly as the dimensionality increases. The paper likely explores how the dimensionality of the data affects the utility bounds of the proposed DP ReLU regression algorithms. Key aspects would include examining how the privacy loss scales with dimensionality and whether the algorithms can maintain reasonable utility in high-dimensional settings. A theoretical analysis would probably involve analyzing the effective dimension of the data and how it impacts the excess population risk. The findings might demonstrate that the utility bounds are not always dependent on the dimension (d), especially under favorable conditions such as faster eigenvalue decay. The results are expected to be supported with rigorous proofs and experiments on datasets with varying dimensionality, which would offer insights into the practical implications of the proposed methods in high-dimensional contexts. The analysis would likely highlight the critical role of eigenvalue decay in determining the performance of DP algorithms in high dimensions, showcasing how data characteristics interact with the privacy-utility trade-off.
Future Works#
Future work could explore extending the DP-GLMtron and DP-TAGLMtron algorithms to handle more complex models, such as deep neural networks. Addressing the limitations imposed by the strong assumptions (e.g., bounded feature vectors) is crucial for broadening the applicability of these methods. Investigating alternative privacy mechanisms beyond the Gaussian mechanism, exploring techniques for adaptive clipping and privacy budget allocation, and providing a more comprehensive analysis of their theoretical guarantees under various data distributions are key areas for improvement. A thorough empirical evaluation on a wider range of datasets and real-world applications is also essential to validate the robustness and effectiveness of the proposed algorithms in diverse settings. Finally, research into the optimal trade-off between privacy, accuracy, and computational efficiency remains a significant challenge worthy of future investigation.
More visual insights#
More on figures
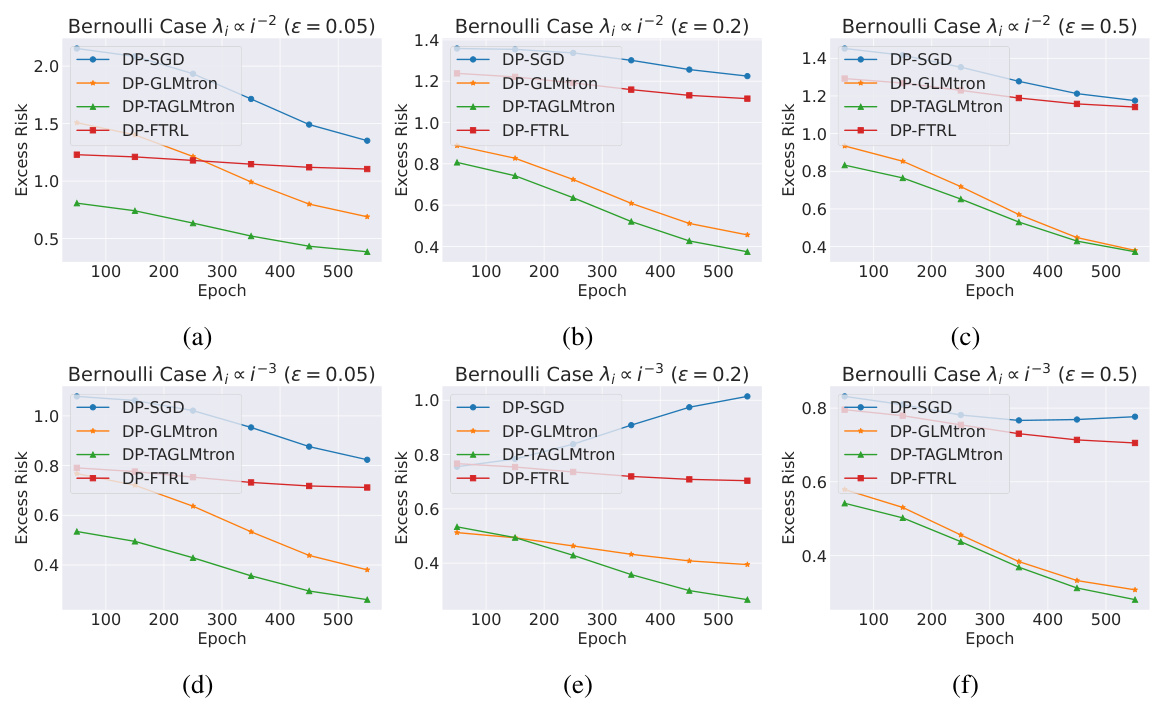
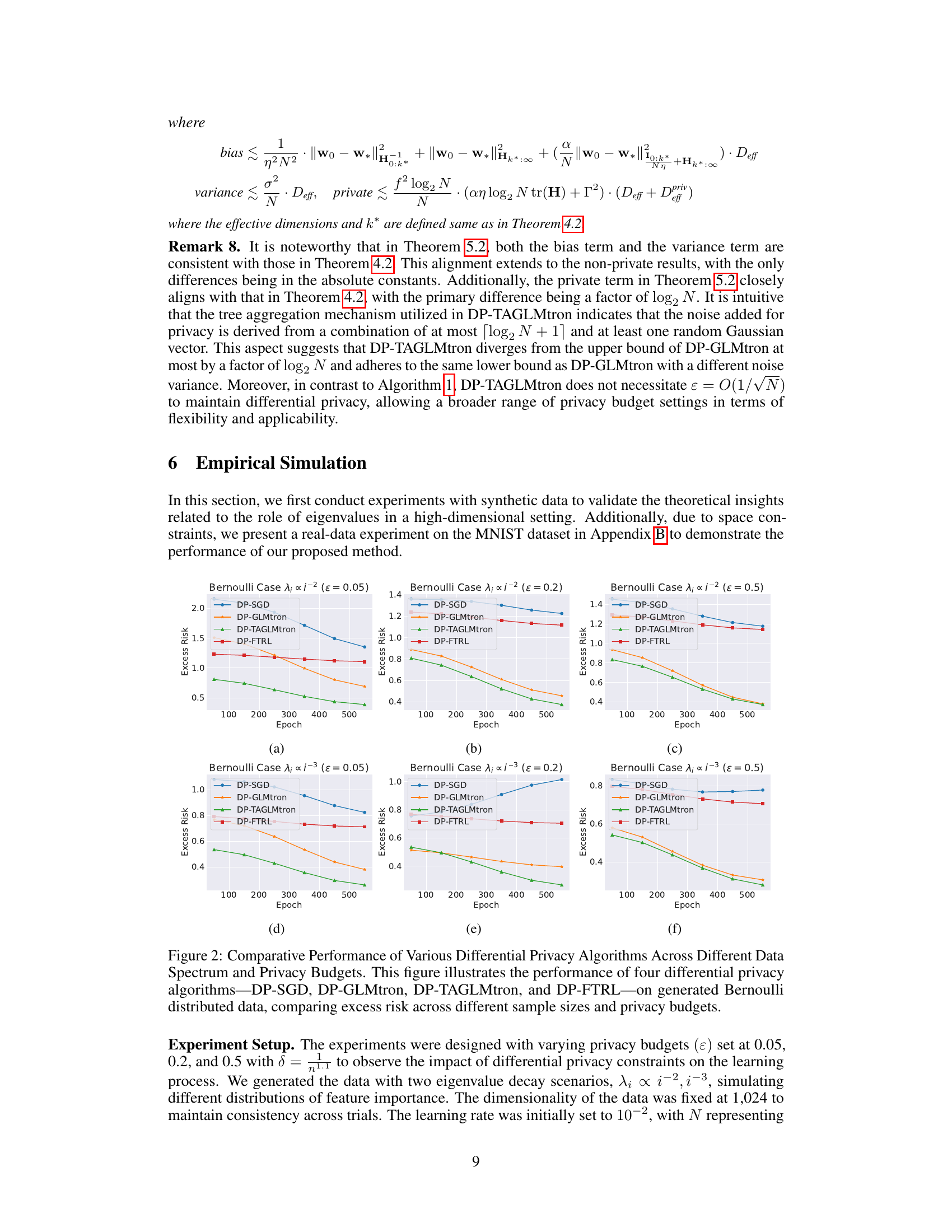
This figure compares the performance of four differential privacy algorithms (DP-SGD, DP-GLMtron, DP-TAGLMtron, and DP-FTRL) on synthetic Bernoulli data with varying eigenvalue decay (λᵢ ∝ i⁻², i⁻³) and privacy budgets (ε = 0.05, 0.2, 0.5). The excess risk (difference between the algorithm’s risk and the optimal risk) is plotted against the number of epochs. The results show that DP-GLMtron and DP-TAGLMtron generally outperform DP-SGD and DP-FTRL, especially as the sample size increases. Additionally, faster eigenvalue decay leads to lower excess risk, highlighting the impact of data distribution on the performance of DP algorithms.
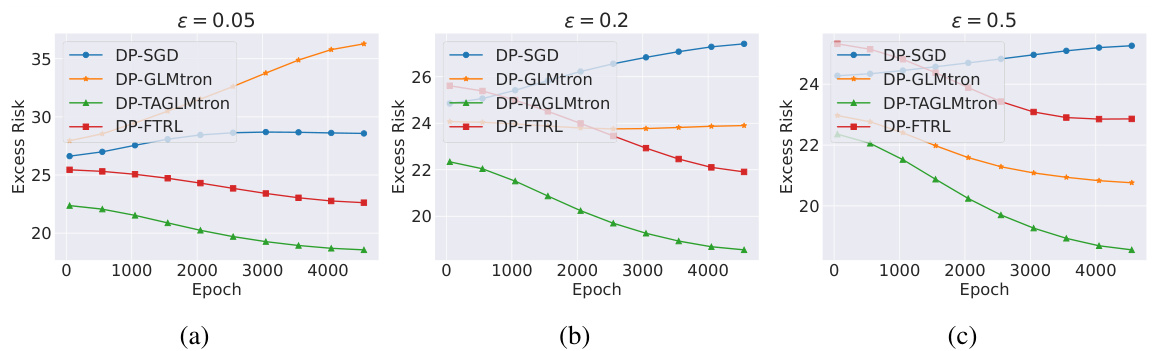
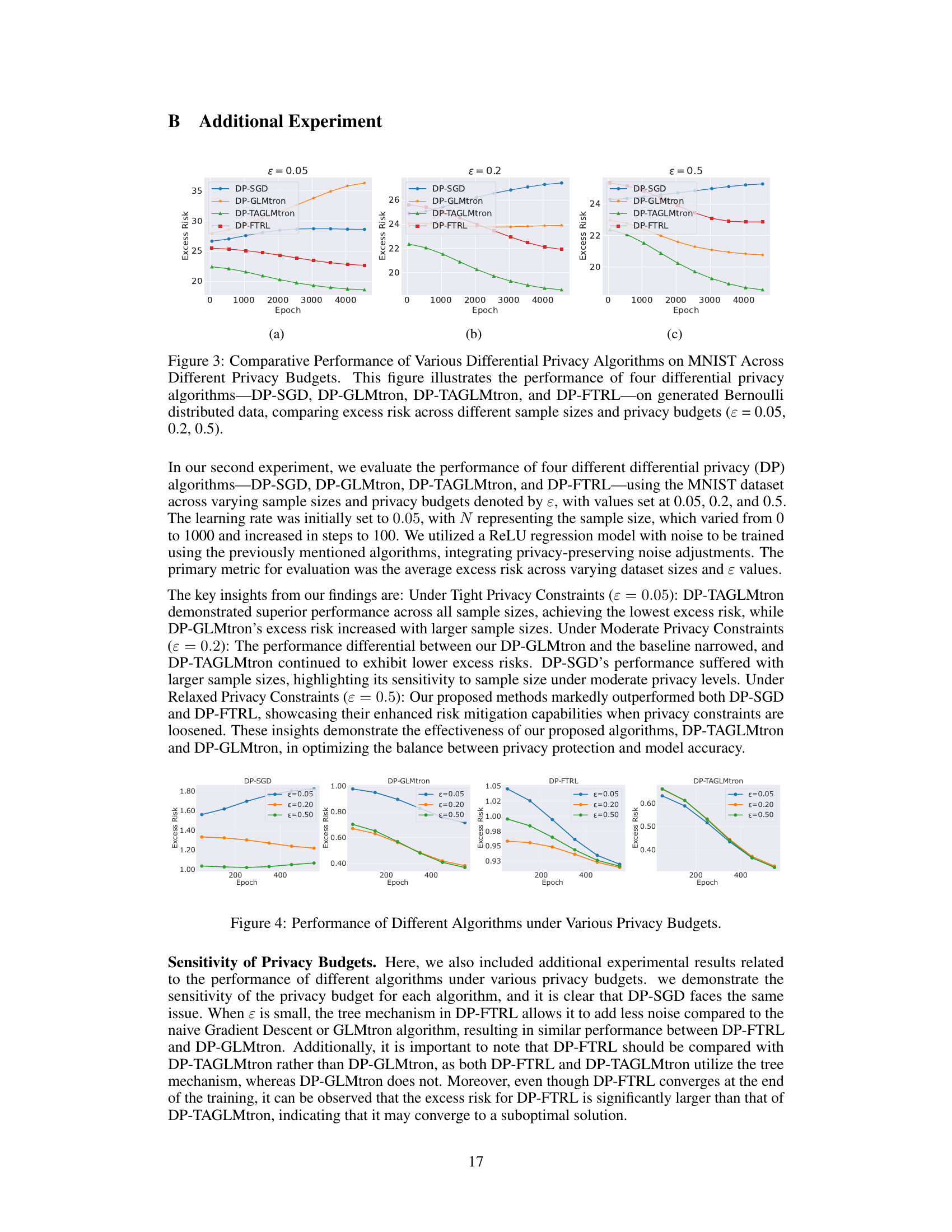
This figure compares the performance of four different DP algorithms (DP-SGD, DP-GLMtron, DP-TAGLMtron, and DP-FTRL) on the MNIST dataset under different privacy budgets (ε = 0.05, 0.2, and 0.5). The x-axis represents the number of epochs, and the y-axis represents the excess risk. The figure shows how the excess risk changes with different algorithms and privacy levels for various sample sizes. It demonstrates the effectiveness of DP-GLMtron and DP-TAGLMtron compared to DP-SGD and DP-FTRL.

This figure compares the performance of four differential privacy algorithms (DP-SGD, DP-GLMtron, DP-TAGLMtron, and DP-FTRL) on synthetic Bernoulli data with eigenvalue decay. It shows excess risk (a measure of model accuracy) across different sample sizes and privacy budgets (epsilon values). The results demonstrate the impact of eigenvalue decay rate and privacy budget on model performance, highlighting the relative effectiveness of the proposed DP-GLMtron and DP-TAGLMtron algorithms.
Full paper#