↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many real-world problems can be framed as combinatorial optimization problems, such as finding the smallest set of vertices in a graph that covers all edges (Minimum Vertex Cover). Solving these problems efficiently is crucial, especially for large-scale applications. However, existing approaches often struggle with the computational complexity and energy demands, particularly for complex variants like Hypergraph Minimum Vertex Cover (HMVC).
This research tackles this issue by proposing a new method using Spiking Neural Networks (SNNs) that directly solves HMVC without needing any extra steps like transforming the problem into a simpler form. Their SNN architecture incorporates a clever constraint checking mechanism to ensure feasibility. Experiments on a neuromorphic chip show that this approach not only produced high-quality solutions but also significantly outperformed traditional methods in terms of energy efficiency, speed and solution quality.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in neuromorphic computing and combinatorial optimization. It presents a novel, energy-efficient solution for a complex problem (Hypergraph Minimum Vertex Cover), demonstrating the potential of SNNs for tackling challenging optimization tasks. Its success in outperforming traditional methods on neuromorphic hardware opens exciting avenues for future research in designing specialized SNN architectures for solving similar combinatorial problems.
Visual Insights#

This figure compares three different Spiking Neural Networks (SNNs). (a) shows a 3-uniform hypergraph representing the Hypergraph Minimum Vertex Cover (HMVC) problem. (b) illustrates a QUBO-based SNN for solving the HMVC problem using the QUBO formulation, which incorporates slack variables. (c) presents the Slack-Free (SF) HMVC SNN proposed by the authors. This novel architecture doesn’t use the QUBO formulation and incorporates custom feedback neurons for constraint checking and correction.
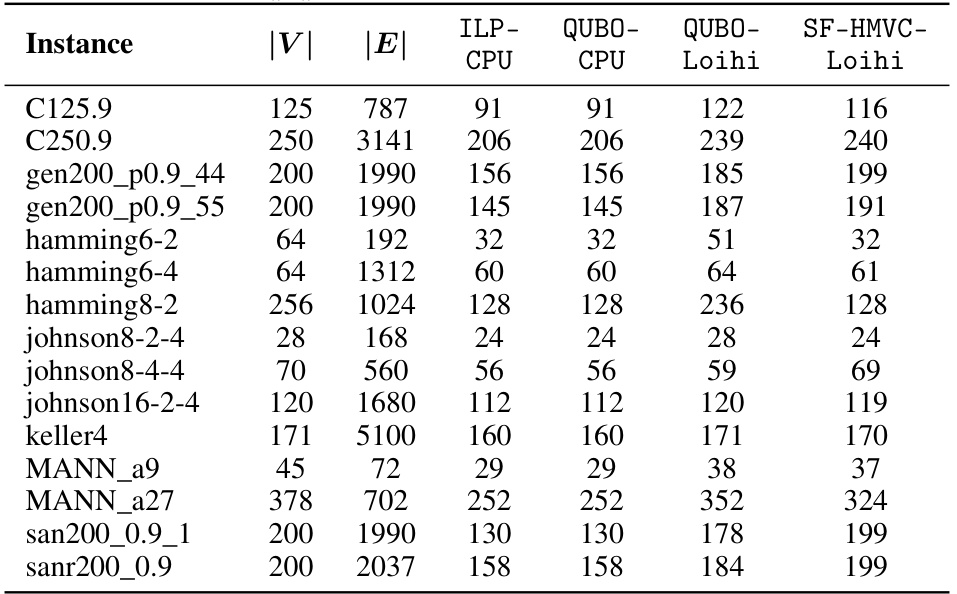
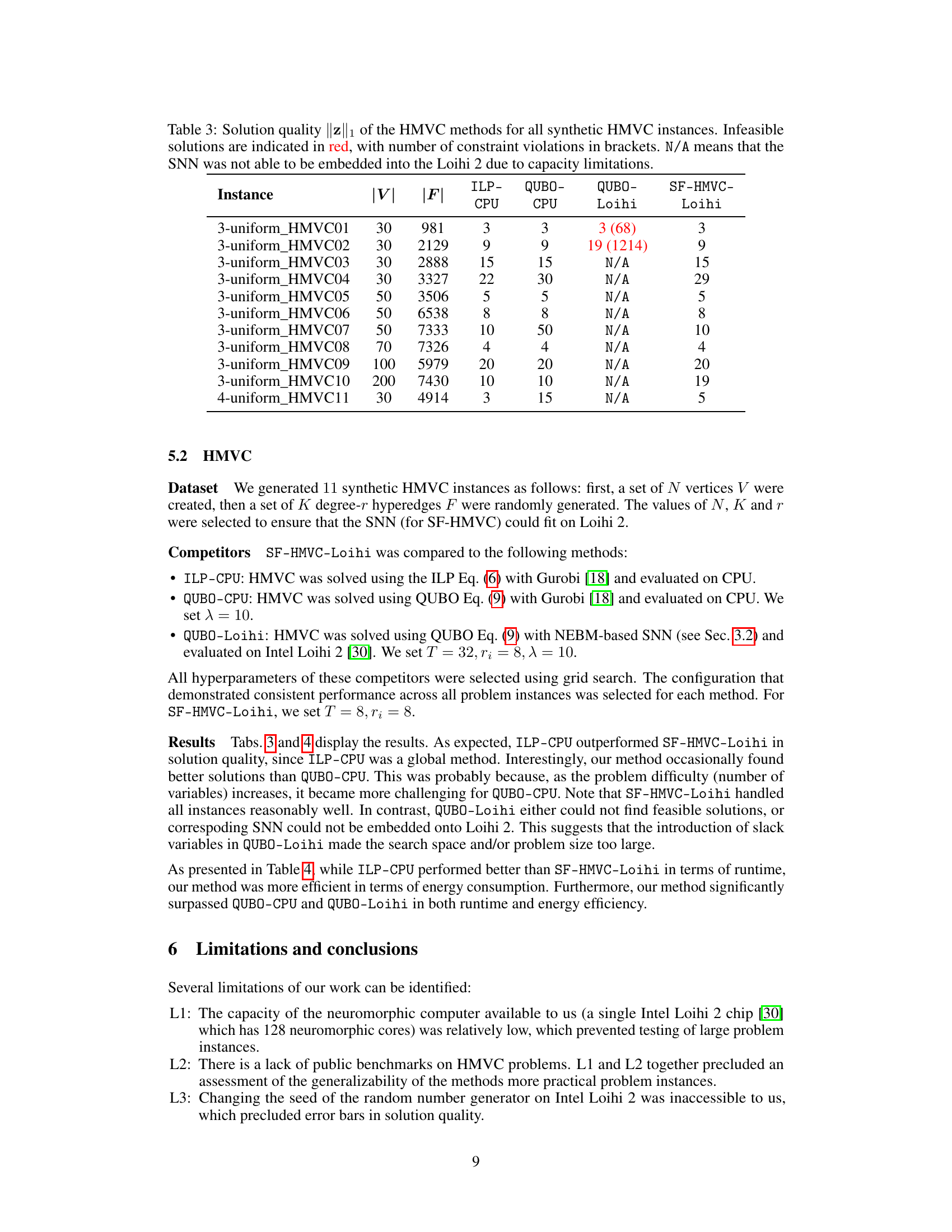
This table presents the solution quality, in terms of the number of vertices in the minimum vertex cover, obtained by four different methods for solving the Minimum Vertex Cover (MVC) problem on a set of benchmark instances from the DIMACS dataset. The methods compared are: ILP-CPU (Integer Linear Programming solved on a CPU), QUBO-CPU (Quadratic Unconstrained Binary Optimization solved on a CPU), QUBO-Loihi (QUBO solved using a Spiking Neural Network on Intel Loihi), and SF-HMVC-Loihi (Slack-Free HMVC solver using an SNN on Intel Loihi). The table shows the number of vertices (|V|) and edges (|E|) for each instance and the solution quality obtained by each method. The results illustrate the performance of the proposed SF-HMVC-Loihi method compared to existing methods, showing its ability to find high-quality solutions, especially on larger and more complex instances.
In-depth insights#
SNN for HMVC#
The proposed research explores the application of Spiking Neural Networks (SNNs) to solve the Hypergraph Minimum Vertex Cover (HMVC) problem. A key innovation is the slack-free formulation, eliminating the need for penalty terms and slack variables often introduced in traditional QUBO reformulations. This approach, reducing the search space, improves the efficiency and effectiveness of the SNN solver. The architecture incorporates additional spiking neurons with a constraint checking and correction mechanism, directly guiding the network toward feasible solutions. Experiments on neuromorphic hardware demonstrate the method’s superiority over existing SNN-based QUBO solvers, achieving consistently high-quality solutions for HMVC on various instances where QUBO methods frequently fail. Energy efficiency is also significantly improved compared to CPU-based global solvers, highlighting the potential of specialized SNN architectures for combinatorial optimization problems.
Slack-Free Design#
A slack-free design in the context of a spiking neural network (SNN) for solving combinatorial optimization problems like the hypergraph minimum vertex cover (HMVC) is a significant advancement. Traditional methods often introduce slack variables to handle constraints, increasing the problem’s complexity and hindering SNN efficiency. A slack-free approach directly incorporates constraints into the network architecture, eliminating the need for penalty terms and reducing the search space. This is achieved by using a combination of non-equilibrium Boltzmann machine (NEBM) neurons for variable representation and custom feedback neurons for constraint enforcement. This novel architecture enables the SNN to converge to feasible solutions more efficiently and with measurably less energy consumption compared to methods relying on QUBO reformulations and global solvers. The design’s effectiveness hinges on the precise interaction between NEBM and feedback neurons, cleverly balancing the exploration of solution space and the enforcement of constraints. This approach demonstrates a shift towards handcrafted SNNs tailored for specific problems, offering superior performance and efficiency compared to generic QUBO-based solutions. This offers a more promising path for deploying SNNs on neuromorphic hardware for practical combinatorial optimization problems.
Loihi2 Results#
An analysis of a hypothetical ‘Loihi2 Results’ section in a research paper would likely focus on the performance of a novel algorithm or model implemented on Intel’s Loihi 2 neuromorphic chip. Key aspects would include a comparison of the Loihi 2 implementation against other methods, such as CPU-based solutions or other neuromorphic platforms. Metrics like speed, energy efficiency, and solution quality would be essential for demonstrating the advantages of using Loihi 2. The discussion should delve into the specific hardware and software configurations employed, including details on the number of neurons, synapse weights, and algorithmic parameters. Furthermore, an in-depth analysis might explore the scalability of the Loihi 2 implementation across problem sizes or complexities, possibly including limitations encountered and how these could affect real-world deployment. The results should be presented with statistical significance, possibly using error bars or confidence intervals. The overall conclusion would assess the potential of Loihi 2 for accelerating the specific task and highlight any notable tradeoffs between performance and resource consumption.
Scalability Analysis#
A scalability analysis of a novel algorithm or system is crucial for evaluating its practical applicability. The analysis should quantitatively assess how the algorithm’s performance changes as the size of the input data or problem increases. It’s important to consider various factors that might affect scalability, such as memory usage, processing time, and computational complexity. For instance, an analysis might reveal that the algorithm exhibits linear scalability, meaning that performance increases linearly with input size, or it might demonstrate exponential scalability, implying significantly worse performance for larger inputs. A thoughtful scalability analysis will often compare the algorithm against existing methods and highlight where it excels or falls short. Furthermore, identifying the computational bottlenecks of the algorithm helps in designing strategies to optimize performance and extend scalability. The analysis should be supported by both theoretical estimations (e.g., Big O notation) and experimental evaluations using a wide range of datasets, ensuring the conclusions are robust and reliable.
Future Works#
Future work could explore several promising avenues. Scaling the slack-free SNN to larger hypergraphs is crucial, potentially through architectural modifications or leveraging more powerful neuromorphic hardware. Investigating the impact of different neuron models and network topologies on performance is warranted. Addressing the limitations of the current energy measurement by employing more precise techniques would enhance the accuracy of energy efficiency comparisons. Exploring alternative constraint handling methods, perhaps incorporating online learning techniques or advanced feedback mechanisms, could enhance the SNN’s efficiency and robustness. Extending the methodology to solve related combinatorial problems, such as set cover or hitting set problems, while maintaining energy efficiency, would further demonstrate the algorithm’s versatility. Finally, thorough theoretical analysis to understand the algorithm’s convergence properties and scalability limits should be pursued.
More visual insights#
More on tables
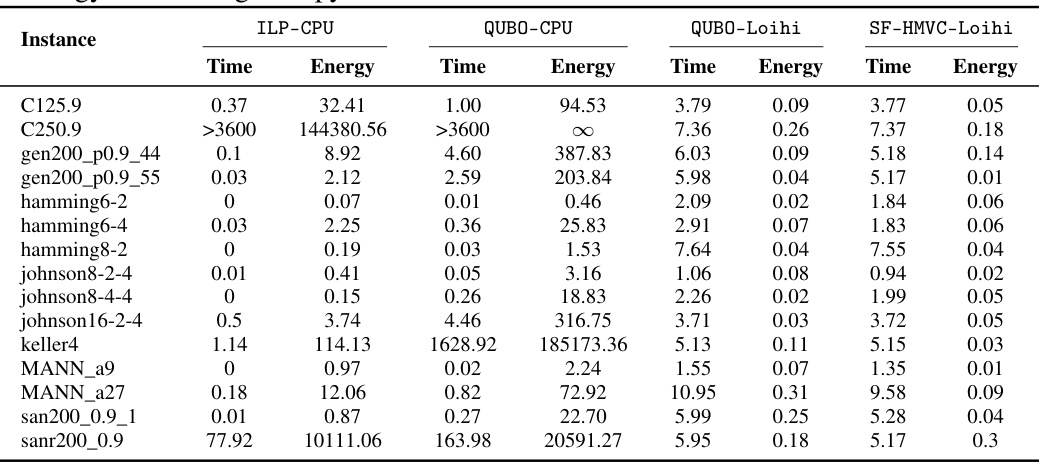
This table presents a comparison of four different methods for solving the Minimum Vertex Cover (MVC) problem: ILP-CPU, QUBO-CPU, QUBO-Loihi, and SF-HMVC-Loihi. For each method, the table shows the runtime in seconds and energy consumption in Joules across fifteen different instances of the MVC problem from the DIMACS benchmark dataset. The symbol ∞ indicates that the energy consumption was too high to measure accurately using the pyJoules tool.
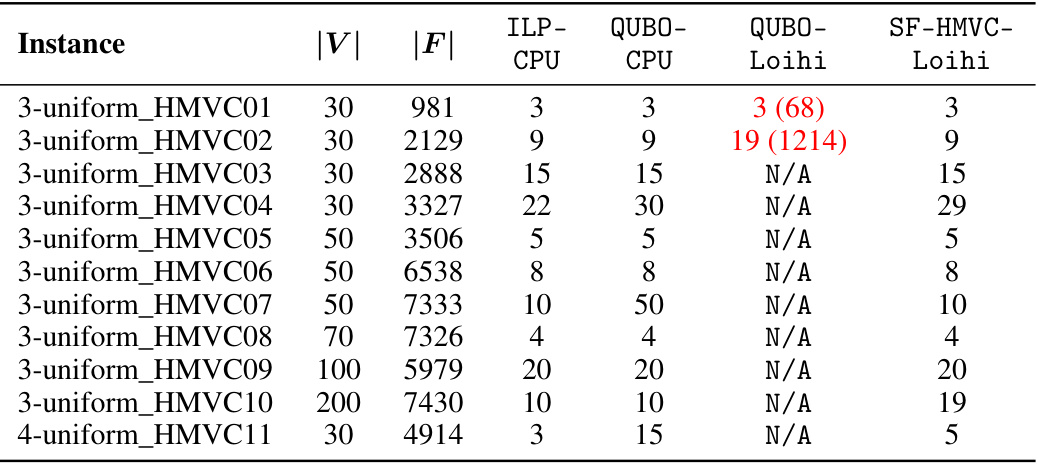
This table presents a comparison of the solution quality (measured by the L1 norm of the solution vector z) for the Hypergraph Minimum Vertex Cover (HMVC) problem across different methods. The methods compared include: ILP solved on CPU, QUBO formulation solved on CPU, QUBO formulation solved on Loihi neuromorphic chip using an established SNN, and the proposed SF-HMVC method on Loihi. The table shows that the proposed SF-HMVC method performs comparably to or better than the others in terms of solution quality and feasibility, while the QUBO methods, especially on Loihi, fail to produce feasible solutions for many instances due to capacity limitations.
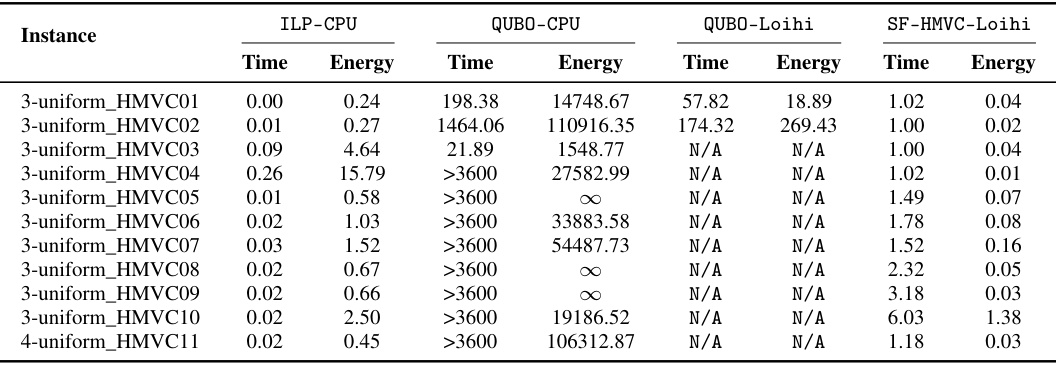
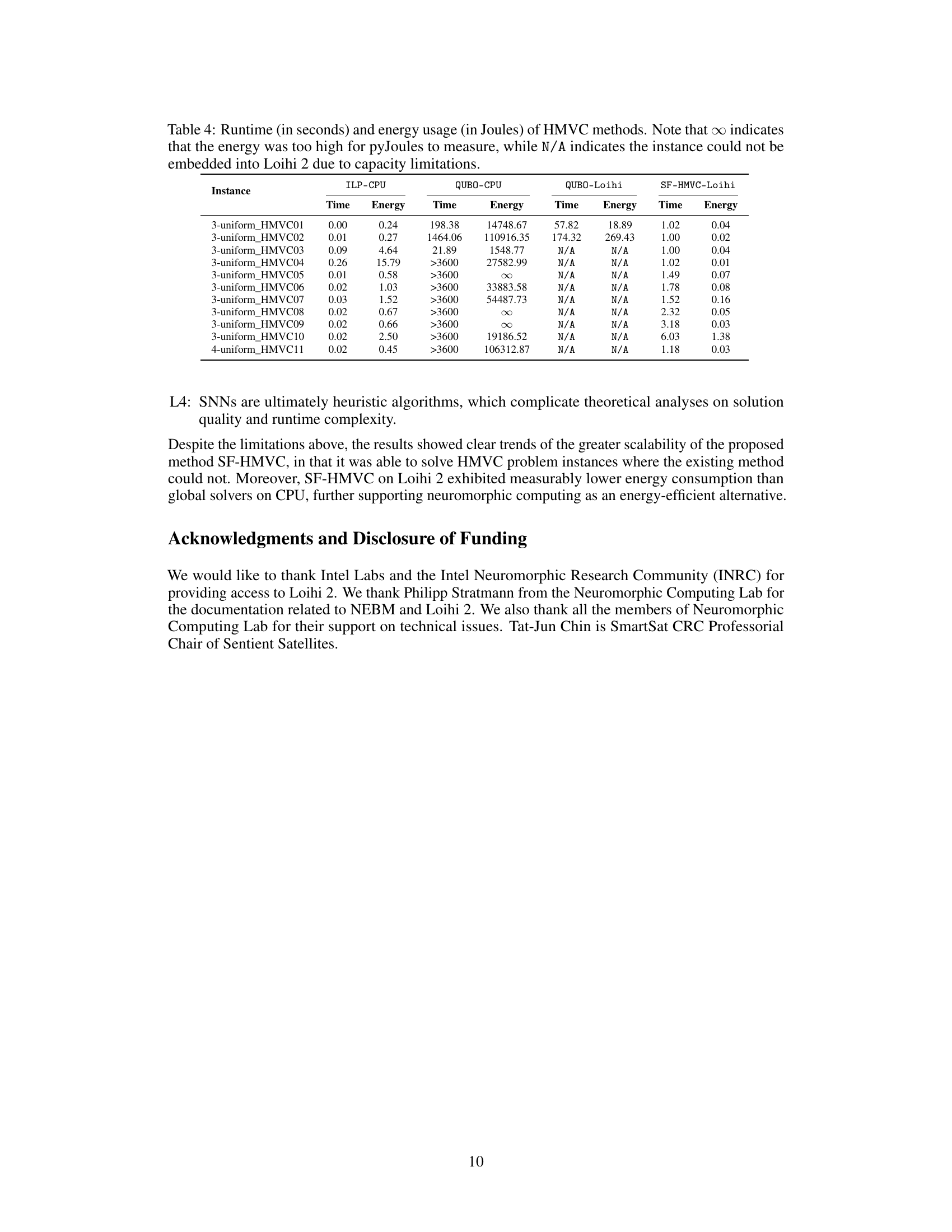
This table presents the runtime and energy consumption results for solving the Hypergraph Minimum Vertex Cover (HMVC) problem using four different methods: ILP-CPU, QUBO-CPU, QUBO-Loihi, and SF-HMVC-Loihi. For each method and instance, the time taken to find a solution (in seconds) and the energy consumed (in Joules) are provided. Note that some energy values are infinitely large or unavailable (N/A) due to hardware limitations on Intel Loihi 2.
Full paper#