How Does Black-Box Impact the Learning Guarantee of Stochastic Compositional Optimization?

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it bridges the gap in understanding the learning guarantees of derivative-free stochastic compositional optimization (SCO). Its findings on the impact of black-box settings and the provided learning guarantees for vertical federated learning (VFL) are highly relevant to the ongoing research in SCO and its applications, paving the way for improved algorithms and a better theoretical understanding of this important class of optimization problems.

Visual Insights

#

This table compares the generalization guarantees of several stochastic compositional optimization (SCO) algorithms (SCGD, SCSC) and stochastic gradient descent (SGD) under various assumptions. It shows the generalization error bounds achieved by each algorithm (expressed using Big O notation), along with which assumptions each algorithm satisfies (Lipschitz continuity, smoothness, bounded variance, bounded function, and convexity). The table highlights that the newer work (Theorem 2) provides sharper bounds under milder conditions than prior work.

In-depth insights

#

SCO Black-Box Impact

#

The research explores the effects of a black-box setting on stochastic compositional optimization (SCO). A black-box in this context means that the gradient information of the objective function is unavailable or partially unavailable, necessitating the use of derivative-free optimization methods. The study focuses on how the absence of exact gradient information impacts the learning guarantees, specifically generalization and optimization bounds. The core finding is that using less precise, zeroth-order gradient approximations significantly impacts the learning guarantee. This impact is theoretically analyzed and empirically validated, showing that the quality of gradient approximation directly impacts generalization and optimization performance. The study also examines how the proportion of ‘unknown gradients’ influences the dependence on approximation quality. This work is particularly important because it bridges the gap between theoretical understanding of SCO and real-world applications, where fully differentiable functions are often not available. Overall, the paper’s contribution lies in its detailed theoretical analysis of SCO’s resilience to black-box conditions which opens avenues for future derivative-free SCO algorithms.

Sharper Gen. Bounds

#

The concept of “Sharper Generalization Bounds” in machine learning focuses on improving the accuracy of theoretical guarantees about a model’s performance on unseen data. Traditional generalization bounds often provide loose estimates, making them less informative. Sharper bounds aim to reduce this looseness, offering a more precise understanding of a model’s generalization capability. This is crucial because tighter bounds can lead to better model selection, enabling researchers to choose models that are more likely to generalize well. Furthermore, sharper bounds can guide the development of more effective algorithms, by providing more precise targets for optimization. The pursuit of sharper bounds is an active area of research, requiring novel techniques in statistical learning theory and often involving careful analysis of specific model properties and algorithms. Addressing non-convexity and handling compositional objectives are significant challenges in achieving tighter generalization bounds, requiring advanced theoretical tools.

VFL Learning Guarantees

#

The heading ‘VFL Learning Guarantees’ suggests a focus on establishing theoretical bounds for the performance of Vertical Federated Learning (VFL) algorithms. This is crucial because VFL, by its nature of distributed and privacy-preserving computation, presents unique challenges to traditional analysis methods. Reliable learning guarantees would demonstrate the algorithm’s convergence and generalization capabilities, providing confidence in its predictions and reliability. The analysis would likely involve techniques from statistical learning theory, focusing on factors such as the quality of gradient estimations in a distributed setting, the impact of communication noise, and the effects of data heterogeneity across participating parties. A key aspect would be quantifying the trade-off between privacy preservation and accuracy, showing how different levels of privacy compromise affect learning performance. The work likely presents novel generalization and optimization error bounds for VFL, potentially comparing the performance of different VFL algorithms or different privacy mechanisms. Ultimately, providing rigorous learning guarantees for VFL would significantly enhance trust and adoption of this important technology.

Black-Box Analysis

#

Black-box analysis in machine learning tackles the challenge of understanding and improving models with limited or no access to their internal workings. This approach is crucial when dealing with complex models where the internal mechanisms are opaque or proprietary. A key focus is often on evaluating model performance and behavior through indirect means, such as input-output relationships and sensitivity analyses. Black-box techniques are particularly valuable when dealing with proprietary algorithms or when the model’s complexity prevents direct interpretation. However, the lack of direct access to inner workings means that black-box analysis is inherently limited in its ability to provide deep, causal insights into the model’s decision-making process. Despite these limitations, black-box methods are essential for ensuring fairness, robustness, and safety in machine learning applications, as they help identify biases, vulnerabilities, and other critical issues without requiring complete model transparency.

Non-convex SCO

#

In the landscape of stochastic compositional optimization (SCO), the assumption of convexity is often made for analytical tractability. However, many real-world applications involve non-convex objective functions, rendering the standard SCO algorithms and their theoretical guarantees inapplicable. A thoughtful exploration of non-convex SCO requires a shift in analytical techniques, potentially leveraging tools like algorithmic stability or techniques that handle non-convexity such as those using co-coercivity or smoothness properties. This would lead to a deeper understanding of convergence rates and generalization bounds for these more challenging scenarios. The implications are profound because non-convexity introduces the possibility of local optima, necessitating new analysis frameworks to characterize the algorithm’s behavior in escaping these suboptimal solutions and attaining near global solutions. The exploration of non-convex SCO necessitates the development of novel analysis and algorithmic strategies and, consequently, opens up new areas of research in optimization theory and machine learning.

More visual insights

#

More on tables

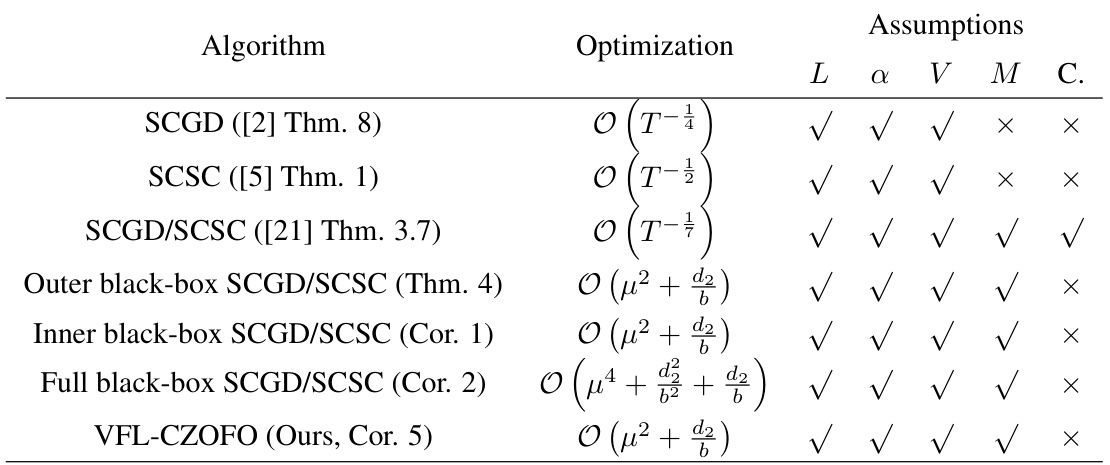
This table compares the optimization guarantees for several SCO algorithms (SCGD, SCSC, and their black-box variants) under different assumptions (Lipschitz continuity, smoothness, bounded variance, bounded function, and convexity). It highlights the convergence rates achieved by each algorithm and indicates which assumptions are satisfied by each.

This table compares the generalization guarantees of several algorithms, including Stochastic Compositional Gradient Descent (SCGD), Stochastically Corrected Stochastic Compositional Gradient Descent (SCSC), and Stochastic Gradient Descent (SGD). It shows the generalization bounds achieved by each algorithm under different assumptions (Lipschitz continuity, smoothness, bounded variance, bounded function, convexity), highlighting the differences in their theoretical guarantees.

This table summarizes the main differences in generalization and optimization results for different theorems and corollaries in the paper, highlighting the specific conditions and techniques used (co-coercivity, almost co-coercivity, special decompositions) for each analysis.

Full paper

#