↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Current methods for assessing quantum computer capabilities have limitations, often failing to account for the complex physics of quantum errors. This leads to inaccurate predictions of which quantum programs a given quantum computer can reliably execute, hindering progress in the field. Existing neural network models, while useful, often struggle to capture the nuances of these errors, especially coherent errors, limiting their predictive power.
This research introduces a novel, quantum-physics-aware neural network architecture. By incorporating fundamental physical principles governing the types and propagation of quantum errors, this model significantly improves the accuracy of capability predictions. The approach utilizes efficient approximations to handle the exponential complexity of error combinations, making it scalable to larger quantum systems (100+ qubits). The model outperforms existing methods, achieving up to 50% reduction in error, and demonstrates accuracy even on out-of-distribution data.
Key Takeaways#
Why does it matter?#
This paper is crucial because it presents a novel approach to assess quantum computer capabilities. It directly addresses the challenge of predicting a quantum computer’s success rate by incorporating quantum physics principles into neural networks. This provides more accurate capability predictions, which is essential for the field’s advancement and impacts resource allocation. The scalability to 100+ qubits opens doors for future research on larger quantum systems.
Visual Insights#

This figure illustrates the architecture of the quantum-physics-aware neural networks (qpa-NNs) used for quantum capability learning. It shows how the network takes a quantum circuit as input, encodes it, predicts error rates using GNN-like structures, and combines these predictions with an efficient approximation of quantum physics to estimate the circuit’s success rate. The figure breaks down the process into multiple steps, highlighting the key components and their interactions.

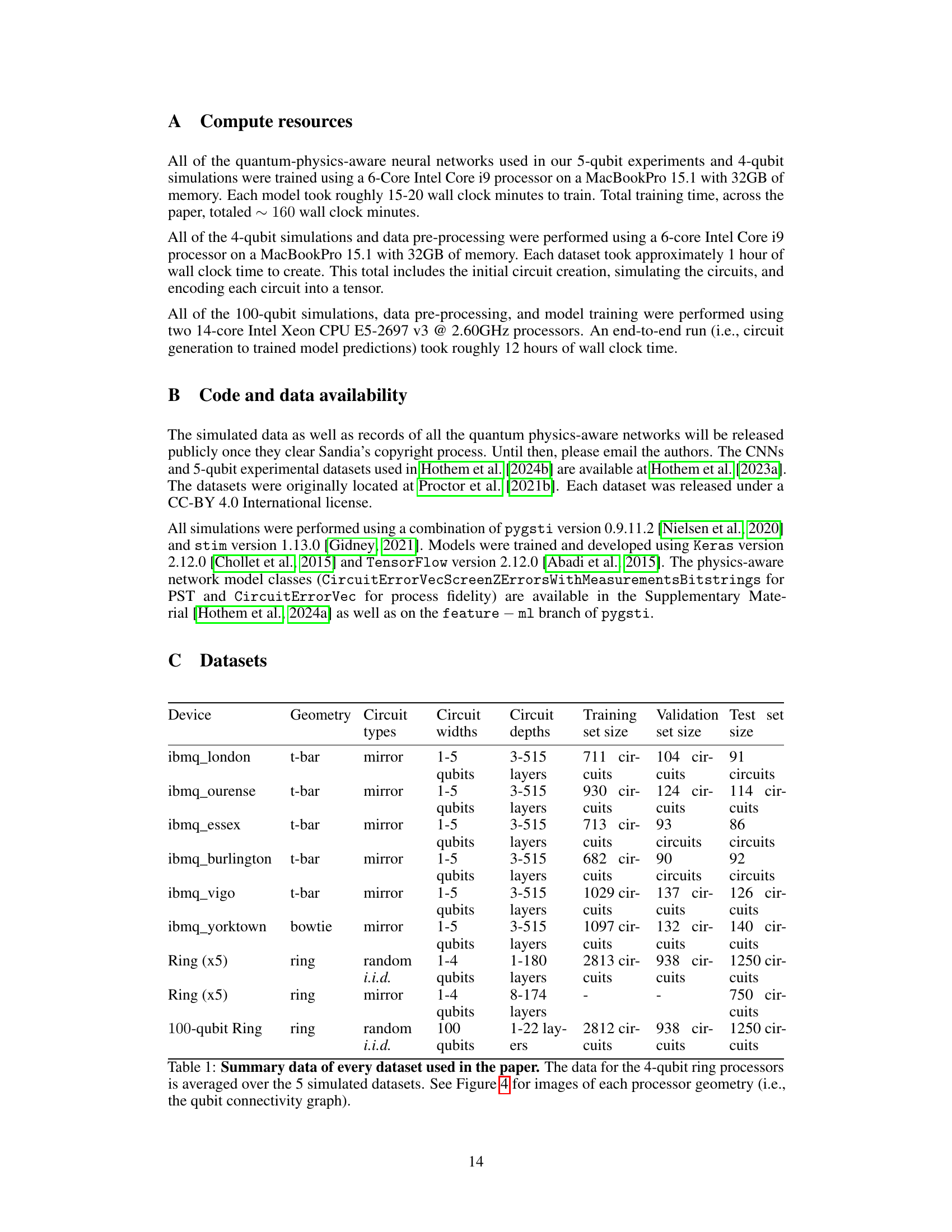
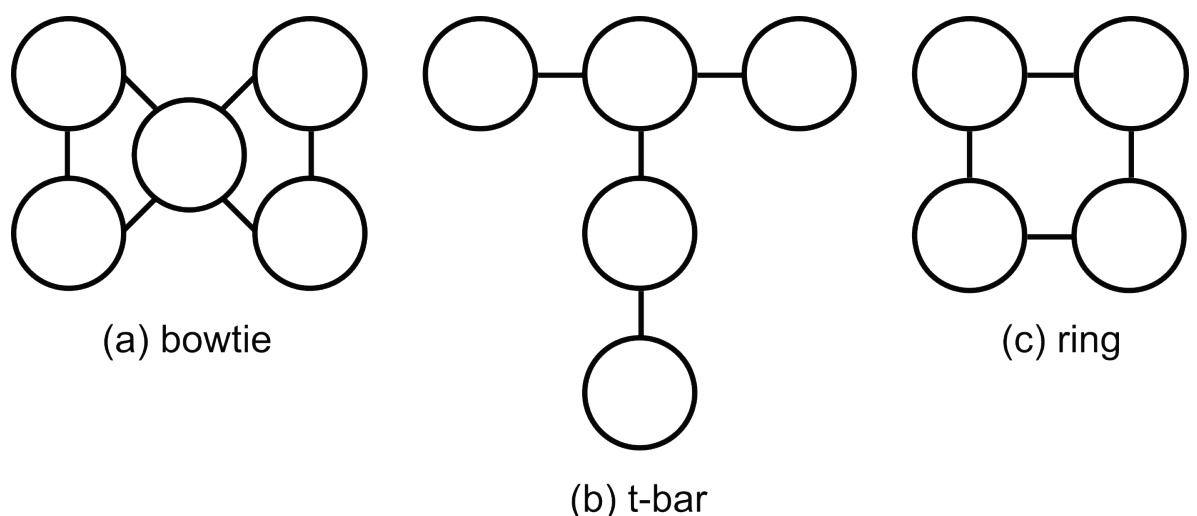
This table summarizes the characteristics of all the datasets used in the paper. It lists the device used (IBM quantum computers or simulated devices), the geometry of the qubit connectivity, the type of circuits used (random i.i.d., random mirror), the number of qubits used, circuit depth (number of layers), and the number of circuits used for training, validation, and testing for each dataset. The data for the 4-qubit ring processors is an average across 5 simulated datasets.
In-depth insights#
Quantum Capability#
Quantum capability, in the context of this research, refers to a quantum computer’s ability to reliably execute quantum programs. It’s a crucial metric because current quantum computers are error-prone, making it challenging to determine which programs will produce accurate results. The paper explores how neural networks can be used to predict this capability. Traditional methods for assessing quantum capability are limited; they typically involve running all possible programs, which is computationally expensive and impractical for larger quantum computers. This research, however, presents a novel approach that uses physics-aware neural networks to predict program execution success more efficiently, ultimately helping to guide the development and optimization of quantum hardware and software. The model’s success in predicting capabilities for devices with 100+ qubits highlights its scalability and potential for practical applications. The approach combines graph neural networks to model the complex physical processes of quantum computation, addressing the limitations of previous methods that failed to learn the intricate quantum physics responsible for real-world errors.
Physics-Aware NN#
The core idea behind Physics-Aware Neural Networks is to integrate physical principles directly into the neural network architecture. This contrasts with traditional neural networks that learn solely from data, often failing to capture underlying physical mechanisms. By incorporating physical knowledge, like quantum error mechanisms in this case, the network becomes more efficient and accurate. This is crucial for quantum capability learning, where standard neural networks struggle due to the complex and often counterintuitive behavior of quantum errors. Improved accuracy and generalization are key advantages; the model learns the physics of the problem rather than just memorizing the training data, making it more robust to variations in input data and capable of better predicting the performance of unseen quantum programs. Scalability is also important; it’s essential for the model to handle larger quantum systems efficiently, which the proposed approach achieves. The specific method uses graph neural network structures and efficient approximations of quantum error physics, optimizing both accuracy and computational requirements.
Experimental Setup#
A well-defined experimental setup is crucial for reproducibility and reliable results. Details on data acquisition, including the specific quantum computers used (models and specifications), circuit generation methods (random, structured, etc.), and error mitigation techniques, should be clearly outlined. Data preprocessing steps should also be documented, such as the handling of noisy data, selection criteria for circuit inclusion (e.g., fidelity thresholds), and any transformations applied. The metrics used to assess performance must be explicitly defined, with an explanation of why these metrics were selected, and the specific ways in which they were calculated. Finally, a clear description of the evaluation methodology is needed, including train/test splits, cross-validation strategies, and any hyperparameter tuning procedures employed. This level of detail ensures transparency and facilitates the validation and comparison of results by other researchers.
Scalability & Limits#
A crucial aspect of any quantum computing algorithm is its scalability. Quantum computers, unlike classical computers, face fundamental limitations in terms of the number of qubits that can be reliably controlled and the extent to which quantum coherence can be maintained. The paper’s investigation into quantum capability learning highlights the challenge of creating accurate predictive models for large-scale quantum devices. The accuracy of the model drops significantly as the number of qubits grows. Therefore, the practical application of such models depends on finding ways to improve their accuracy while maintaining computational feasibility. Furthermore, the physical limitations of quantum hardware, such as noise and error rates, impose constraints on the size and complexity of problems that can be tackled. Therefore, research into fault-tolerant quantum computation and error correction techniques is critical for realizing scalable quantum computers. The current success in reaching 100+ qubits highlights both progress and persistent hurdles. The study reveals that even with advanced techniques like physics-aware neural networks, achieving high accuracy in prediction for larger systems remains a challenge, suggesting that the path towards truly scalable quantum computing is complex and will require significant advancements in both hardware and software. Further improvements in algorithms and error mitigation strategies are needed before the full potential of scalable quantum algorithms can be realized.
Future Research#
Future research directions stemming from this quantum capability learning work could explore several promising avenues. Extending the model to handle non-Markovian noise is crucial for real-world applicability, as this type of noise is prevalent in current quantum computers. Investigating different error models and their impact on model accuracy is another key area. The current study focuses on specific error types; a broader analysis could provide a more robust and generalizable model. Furthermore, exploring the application of this model beyond Clifford circuits to encompass more complex quantum algorithms would significantly enhance its practical relevance. Improving the model’s scalability for even larger quantum devices remains a challenge, particularly as the number of parameters grows exponentially with the number of qubits. Finally, combining this capability learning model with other techniques such as quantum error mitigation and fault-tolerant quantum computing could lead to significant advancements in the field.
More visual insights#
More on figures
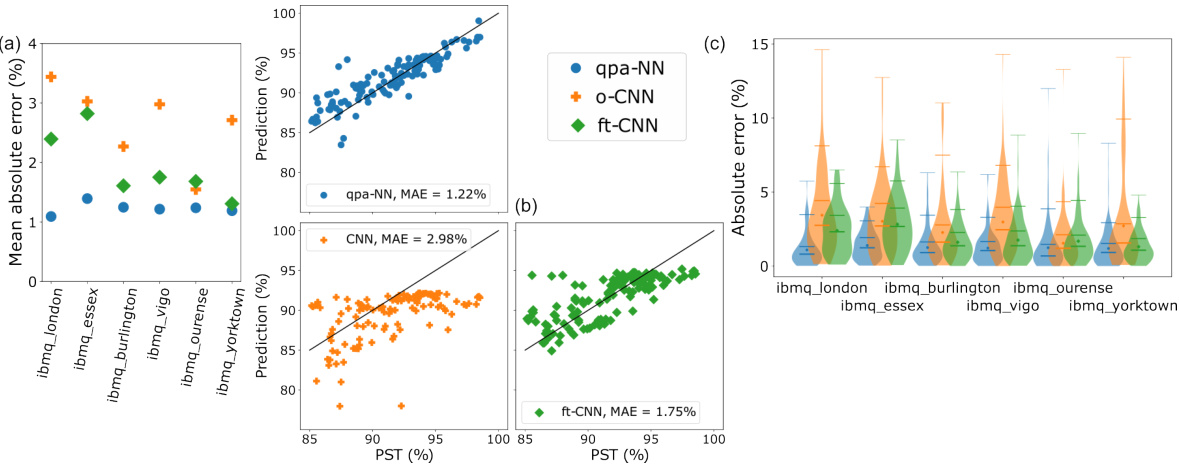
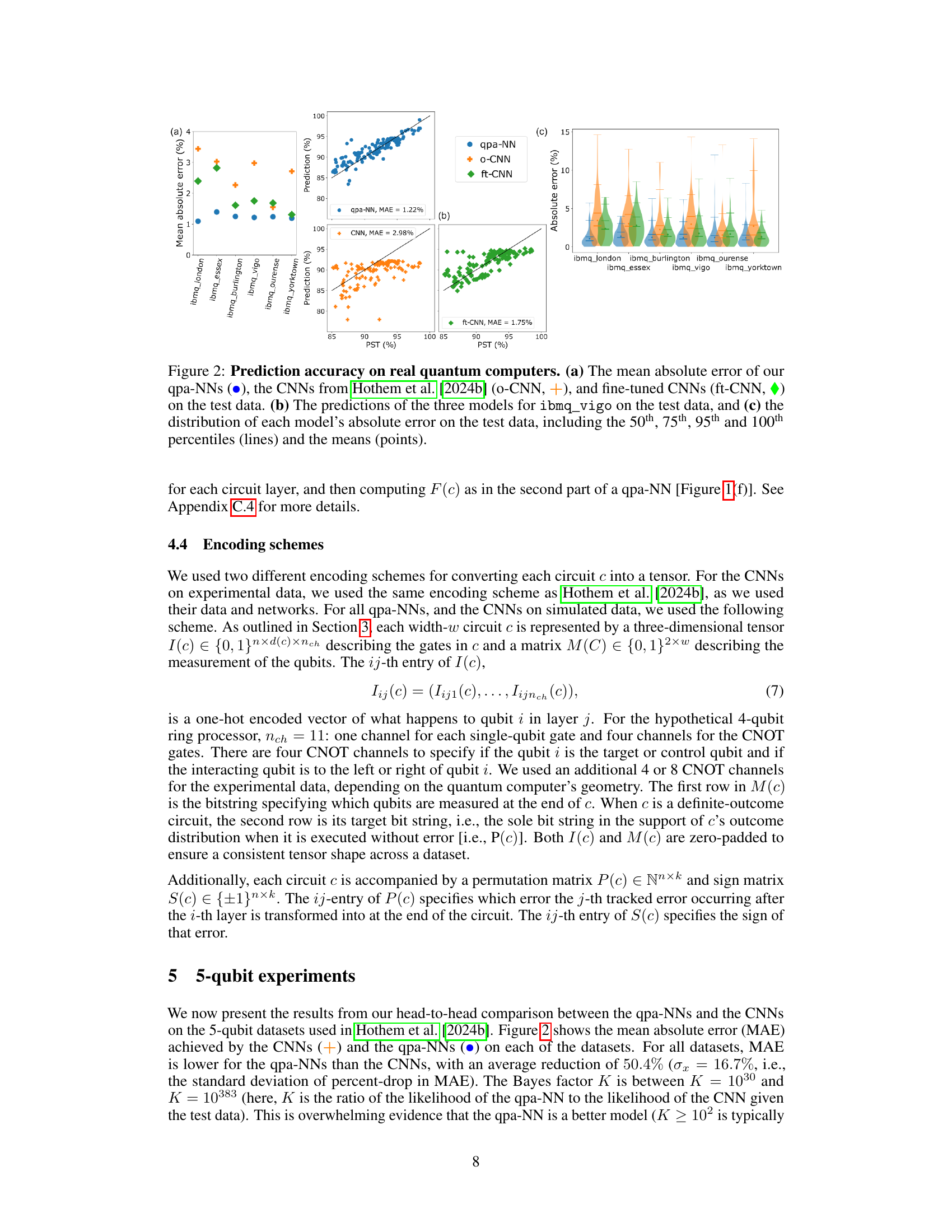
This figure compares the performance of three different models – qpa-NNs, original CNNs, and fine-tuned CNNs – in predicting the success rate (PST) of quantum circuits on real quantum computers. Panel (a) shows the mean absolute error for each model across six different quantum computers. Panel (b) presents a scatter plot showing predictions versus actual values for one of the computers (ibmq_vigo), highlighting the model’s predictive capabilities. Panel (c) provides a violin plot visualization, showing the distribution of absolute errors for each model and each quantum computer, offering a detailed view of performance variability.
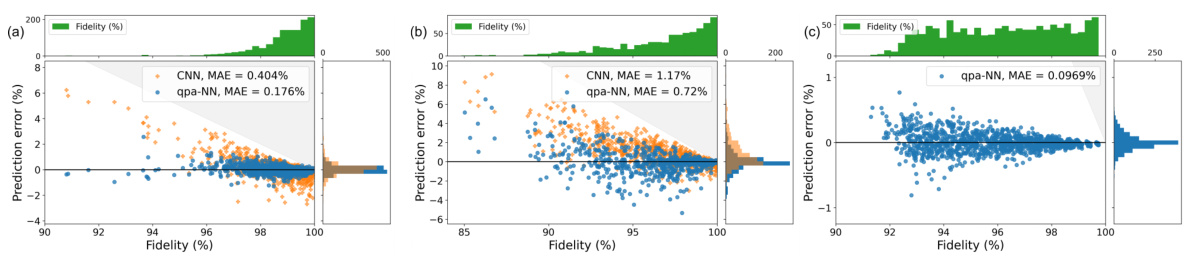
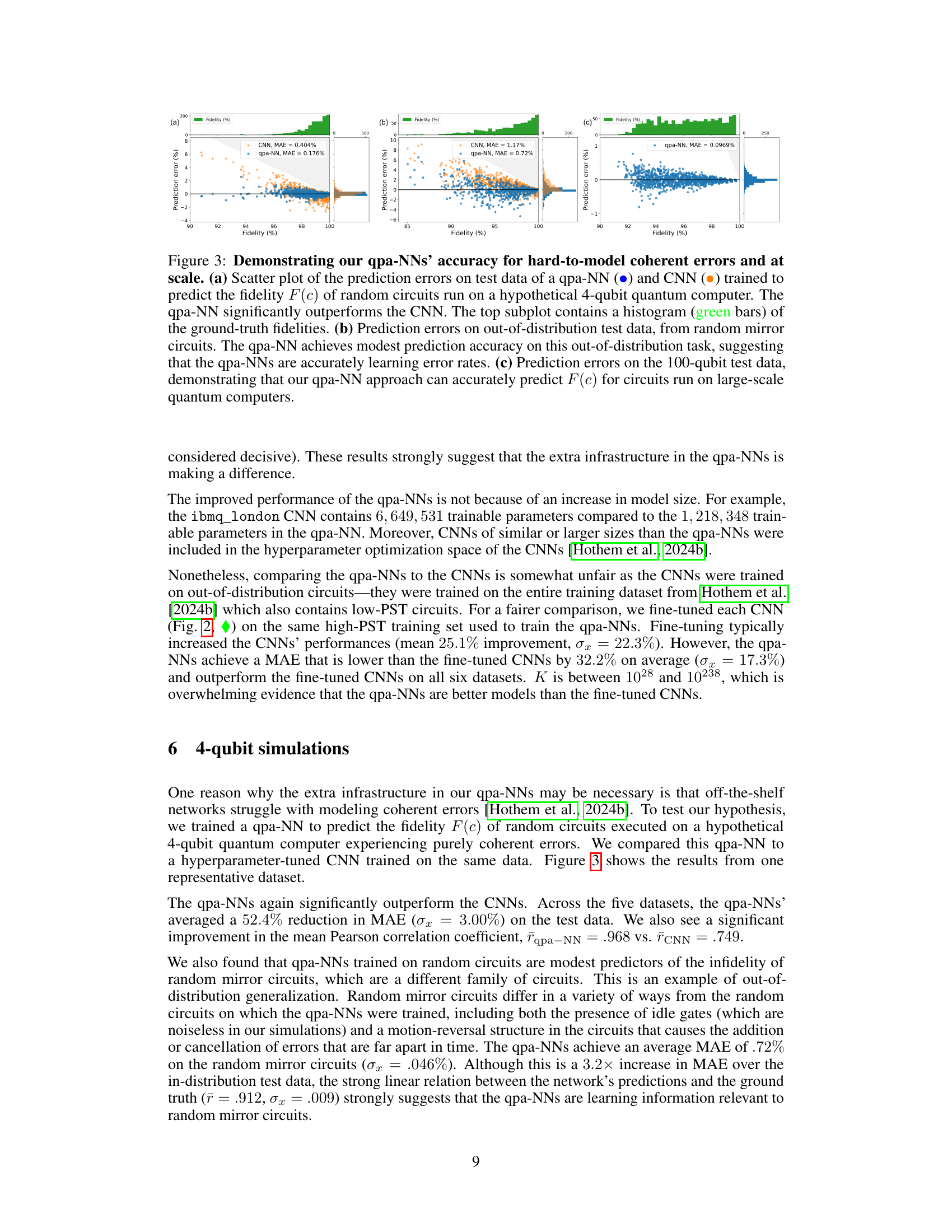
This figure demonstrates the performance of quantum-physics-aware neural networks (qpa-NNs) compared to convolutional neural networks (CNNs) in predicting the fidelity of quantum circuits with coherent errors. Subfigure (a) shows the superior accuracy of qpa-NNs over CNNs on a 4-qubit quantum computer, highlighting their improved ability to handle coherent errors. Subfigure (b) shows that qpa-NNs maintain reasonable accuracy even on out-of-distribution data (random mirror circuits), suggesting they accurately model error rates. Finally, subfigure (c) demonstrates the scalability of qpa-NNs by showing their accurate predictions on a 100-qubit quantum computer.
This figure illustrates the architecture of quantum-physics-aware neural networks (qpa-NNs) for quantum capability learning. It shows how the network takes a quantum circuit as input and predicts the circuit’s success probability by incorporating quantum physics principles and approximating error combinations. It highlights the network’s components, including encoding of quantum circuits, modeling of errors, and the prediction of success rate. Subfigures illustrate a quantum circuit, connectivity graph, error type, one-hot encoding, and the network’s two main parts (N and f) to help visualize the process.
More on tables
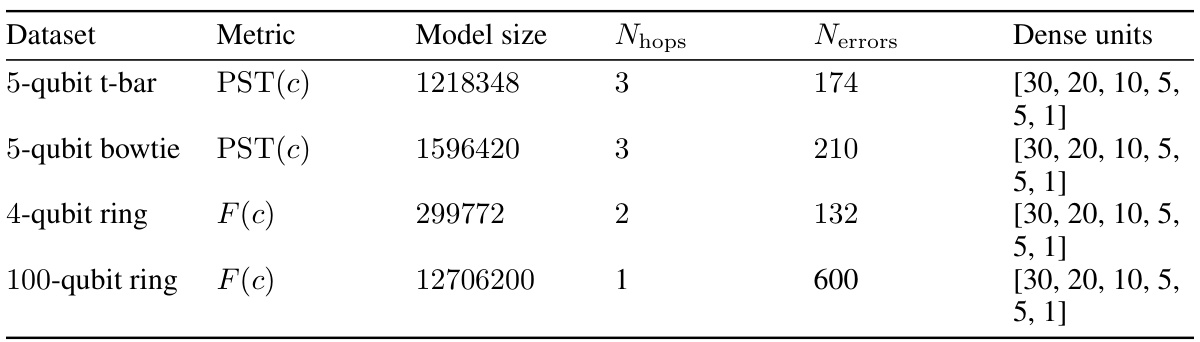
This table summarizes the hyperparameters and model sizes of the quantum-physics-aware neural networks used in the paper. It shows the dataset used, the metric predicted (PST or F(c)), the total number of trainable parameters in the model, the number of hops considered in the connectivity graph when predicting error rates, the number of error types considered, and the structure of the dense layers in the network.

This table presents a comparison of the mean absolute error achieved by the Quantum Physics-aware Neural Networks (qpa-NNs) and Convolutional Neural Networks (CNNs) on six different 5-qubit experimental datasets. It shows the mean absolute error for each model on each dataset. For all datasets, the MAE is lower for the qpa-NNs than the CNNs. Additionally, it provides Bayes factors, comparing the likelihood of the qpa-NN model against both the original CNN model and a fine-tuned version. These Bayes factors demonstrate strong evidence that the qpa-NNs are significantly better models.

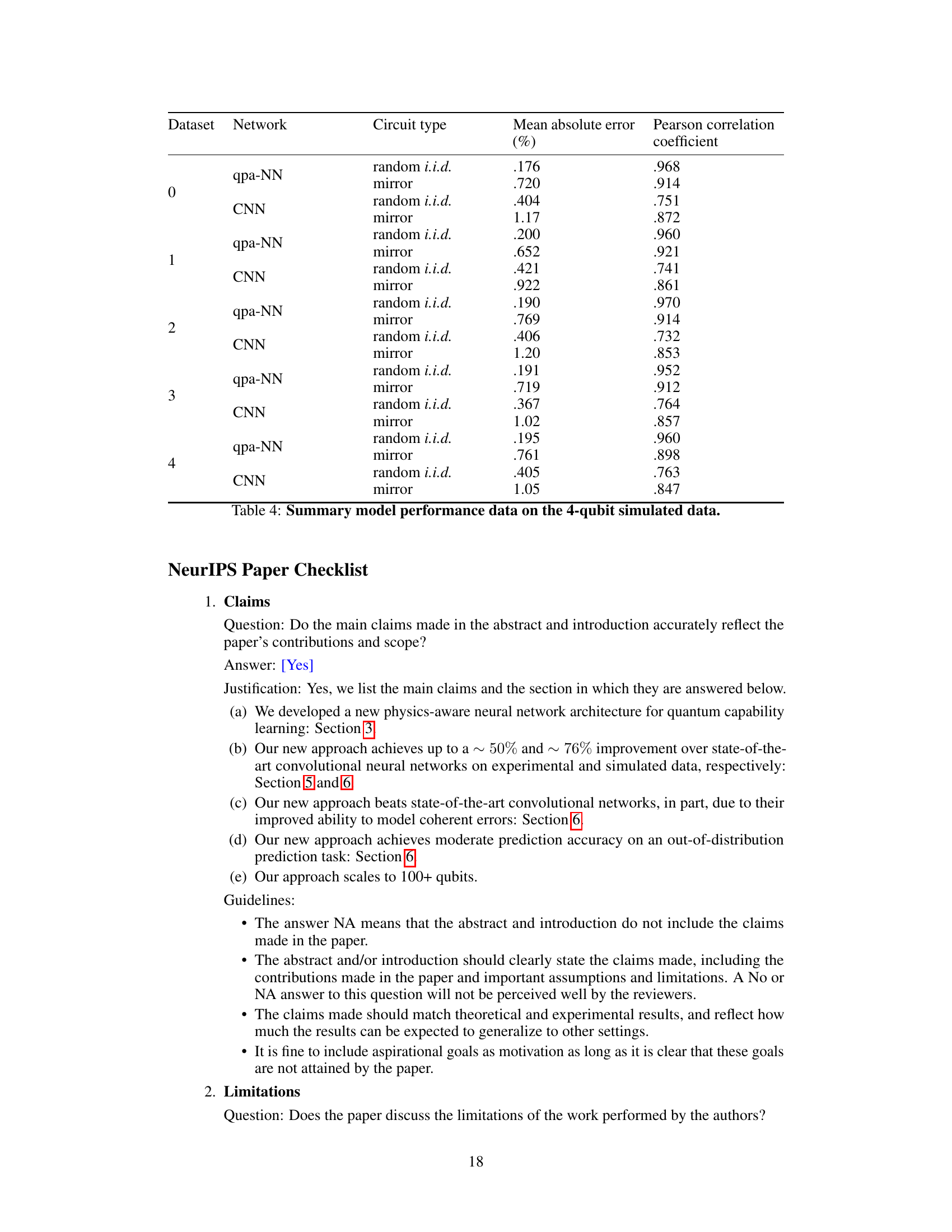
This table presents a comparison of the performance of qpa-NNs and CNNs on a dataset of simulated 4-qubit quantum computations. The dataset includes both random and mirror circuits, each with high fidelity (above 85%). For each model and circuit type, the table shows the mean absolute error (%) and Pearson correlation coefficient. The results illustrate that the qpa-NNs consistently outperform CNNs across all datasets, indicating a significant improvement in prediction accuracy for learning the capabilities of quantum computers.
Full paper#