↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
In-context learning (ICL), where language models solve tasks without parameter updates, is a cornerstone of large language models (LLMs). However, ICL’s theoretical foundations remain poorly understood due to transformers’ complexity. Existing work mostly focuses on simplified models and limited tasks.
This paper addresses this gap by analyzing a two-attention-layer transformer’s training dynamics on n-gram Markov chain data. The researchers prove that gradient descent leads to a model performing a ‘generalized induction head’ mechanism, using a learned feature vector generated by the feed-forward network to select relevant information from past tokens. This mechanism explains how relative positional embedding, multi-head attention, and feed-forward networks work together in ICL.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in AI and machine learning, especially those working with transformers and in-context learning. It provides a theoretical framework for understanding how transformers perform in-context learning, moving beyond empirical observations. This opens new avenues for designing more efficient and interpretable transformer models, advancing the field’s theoretical understanding. The work’s focus on provable training dynamics and feature learning offers valuable insights for improving model training and generalization.
Visual Insights#

This figure is a graphical representation of a two-gram Markov chain. It shows how the (l+1)th token in the sequence (x_l+1) depends only on the two preceding tokens (x_l-1 and x_l). The parent set (pa) is defined as {-1, -2}, indicating that the token depends on the previous token (index l-1) and the token before that (index l-2). This illustrates a simple Markov model showing the conditional dependencies between tokens.
This table summarizes the three-stage training paradigm used in the paper’s experiments and the observed behavior of the model’s parameters at each stage. Stage I focuses on training the feed-forward network (FFN) layer to select the relevant features. Stage II trains the relative positional embedding (RPE) weights in the first attention layer to act as a copier. Stage III focuses on training the weights of the second attention layer to perform a generalized exponential kernel regression. The ‘Description’ column provides a summary of the key dynamics and learning processes at each stage, and the ‘Weights to Train’ column clarifies the specific model parameters being trained in each stage.
In-depth insights#
Induction Head Unveiled#
The concept of the “Induction Head Unveiled” in the context of transformer models is a significant contribution to the field of in-context learning. It moves beyond simply observing the phenomenon of induction heads to providing a theoretical understanding of how these mechanisms emerge during the training process. The research likely delves into the training dynamics of transformers, showing how gradient descent optimizes the model parameters to achieve in-context learning capabilities. This involves a detailed analysis of how different components of the transformer architecture, such as attention mechanisms, feed-forward networks, and normalization layers, work together to create the induction head. A key aspect might be the identification of specific training phases or stages where particular components learn specific roles (e.g., a copying mechanism, a feature selection mechanism, a classification mechanism). The study’s findings probably demonstrate the crucial interplay between these components for the successful emergence of the induction head, offering a comprehensive theoretical framework to explain this key aspect of transformer behavior. The work also likely validates these findings through experiments, demonstrating the convergence of the training process and showing how the model’s behavior aligns with the theory. This provides strong empirical support for the theoretical analysis.
Transformer Dynamics#
Analyzing transformer dynamics involves examining how the model’s internal parameters and their interactions evolve during training. Understanding these dynamics is crucial for improving model performance and generalization. Several factors contribute to these dynamics, including the architecture of the transformer (e.g., number of layers, attention heads), the optimization algorithm used (e.g., gradient descent, Adam), and the characteristics of the training data (e.g., size, distribution, complexity). Research into transformer dynamics often focuses on identifying key patterns and phases in the training process. For instance, some studies have observed an initial phase of rapid learning, followed by a period of slower progress, and finally, a saturation phase where improvements become marginal. Understanding the gradient flow, how information propagates through different layers, and the emergence of specialized attention patterns are key research areas in transformer dynamics. Provable analysis of these dynamics under simplified settings, such as linear transformers or specific data distributions, provides valuable theoretical insights. However, these insights don’t fully capture the complexity of large-scale transformer models. Future work in this area should focus on developing more sophisticated analytical techniques that can handle the complexities of real-world transformer models and datasets.
GIH Mechanism#
The Generalized Induction Head (GIH) mechanism, a core concept in the paper, offers a novel perspective on in-context learning (ICL) in transformers. It posits that successful ICL isn’t solely reliant on the attention mechanism, but rather emerges from the concerted action of multiple transformer components. The GIH framework highlights a three-phase training dynamic: initially, the feed-forward network (FFN) identifies relevant “parent” tokens; subsequently, the first attention layer acts as a copier, replicating these parents; finally, the second attention layer functions as a learned kernel classifier comparing features, ultimately making predictions. This model effectively learns a feature representation by incorporating relative positional embeddings and layer normalization. A crucial aspect is the modified χ²-mutual information which acts as a feature selection metric, guiding the model toward informationally relevant parents and away from redundant data. This provides a more sophisticated view of ICL than previous “induction head” models, extending the theory to account for multiple parent tokens and demonstrating a more complete understanding of the transformer’s ICL capabilities.
Training Convergence#
The concept of “Training Convergence” in the context of machine learning, particularly deep learning models, refers to the process where a model’s parameters stabilize during training. Successful convergence implies that the model has learned to adequately represent the underlying patterns in the data. This is typically indicated by a plateauing of the loss function, which measures the difference between predicted and actual values. The rate of convergence is crucial as faster convergence can save significant computational resources, whereas very slow convergence might signal issues with the model architecture, hyperparameters, or data quality. The theoretical analysis of convergence often involves proving that the model’s optimization algorithm is guaranteed to reach a minimum or a saddle point of the loss function, under certain conditions. Empirical assessment focuses on the behavior of the loss curve and the model’s performance on validation data to determine if acceptable convergence has been achieved. However, complete convergence is not always necessary or even desirable. In some cases, early stopping might yield better generalization performance by preventing overfitting. Factors influencing convergence include the learning rate, batch size, optimizer type, model complexity, dataset characteristics, and the choice of initialization strategies for the model’s parameters.
Future ICL Research#
Future research in in-context learning (ICL) should prioritize a deeper understanding of its theoretical foundations. Current empirical successes mask a lack of theoretical clarity on why ICL works, especially for complex tasks. Bridging this gap requires developing more rigorous mathematical models and analyses of transformer architectures, including examining the interaction between different components (attention, feed-forward networks, normalization). Further work should focus on identifying and quantifying the inductive biases inherent in transformers that enable ICL and clarifying the relationship between ICL and generalization. Investigating how various training methodologies impact ICL performance and exploring the role of different types of data (e.g., structured vs. unstructured) is critical. Finally, research should address robustness issues, such as ICL’s sensitivity to prompt engineering and its performance on noisy or adversarial data. Ultimately, the aim is to move beyond empirical observations and develop a principled understanding of ICL, leading to more efficient and reliable applications.
More visual insights#
More on figures
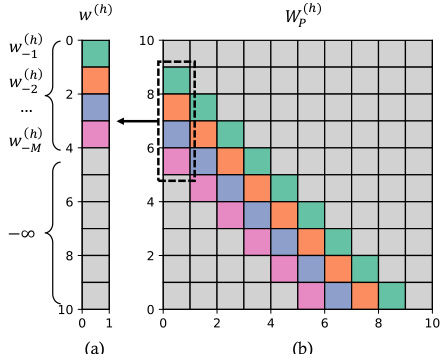
This figure illustrates how relative positional embeddings (RPE) are used in the transformer model. Panel (a) shows the RPE vector w(h) for a single head, where each element corresponds to a relative position within a window of size M. Panel (b) shows the resulting RPE matrix W(h), which is used to compute attention scores between tokens. Note that W(h) only considers tokens within a window of size M, and that the values outside of this window are set to -∞. This is implemented using the relationship W(h)(i,j) = w(h)_|i-j| if 1 ≤ |i - j| ≤ M and W(h)(i,j) = -∞ otherwise.

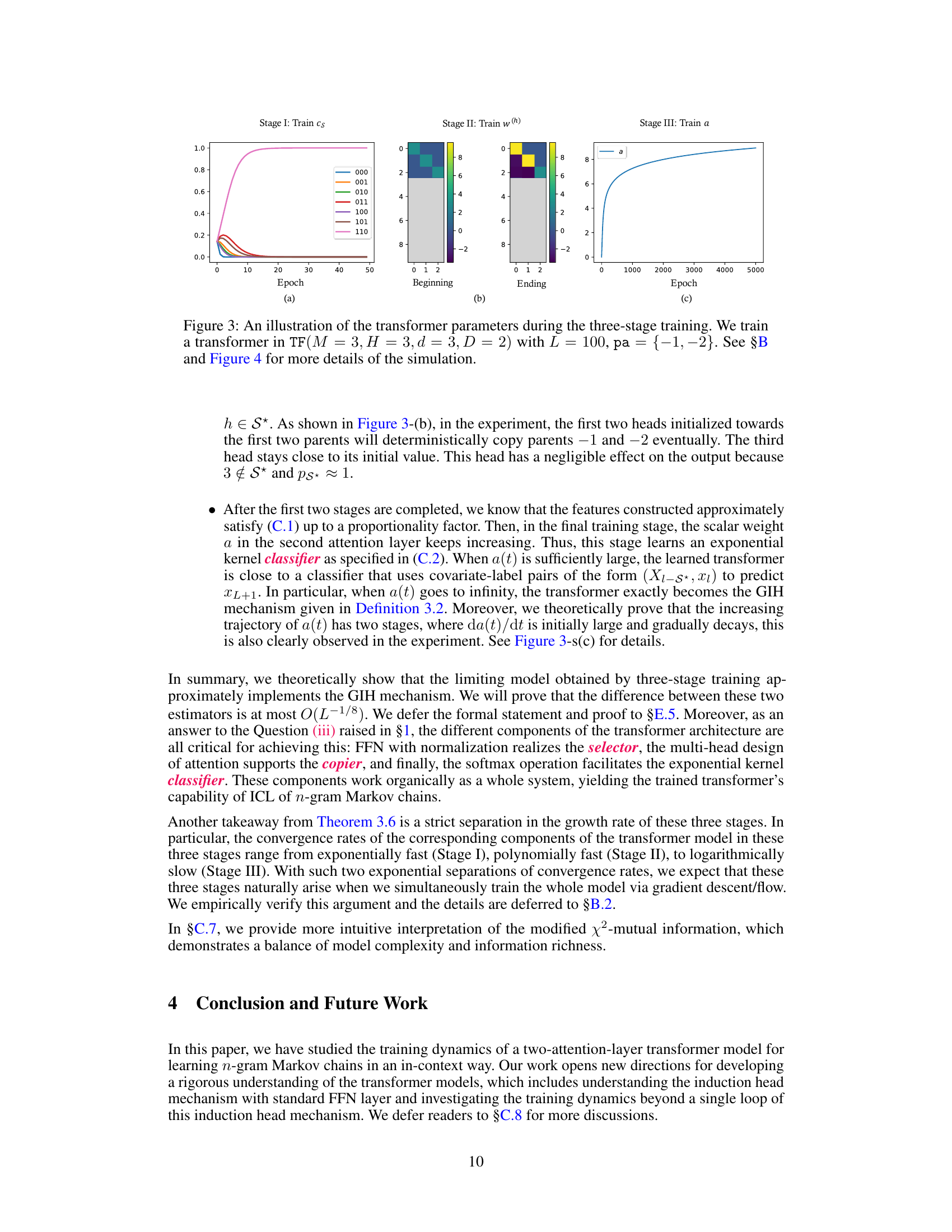
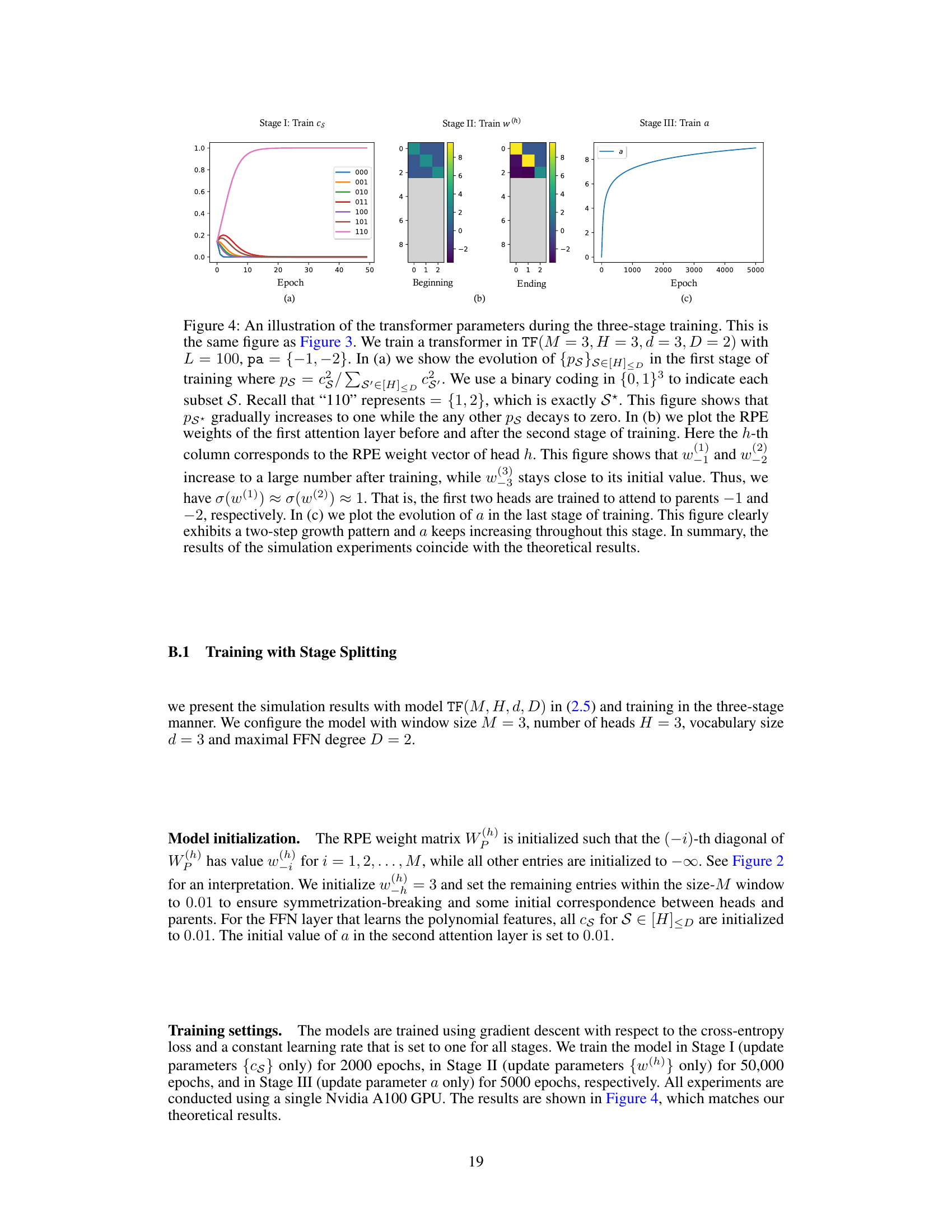
This figure shows the training dynamics of a two-attention-layer transformer model. The training process is divided into three stages, each focusing on a specific subset of weights. Stage I trains the feed-forward network (FFN) weights, which aims to select relevant features. Stage II updates the relative positional embedding (RPE) weights of the first attention layer to establish copying mechanisms. Finally, Stage III trains the second attention layer’s weight to aggregate the features and produces the final output. The plot demonstrates the changes in these parameters across these stages, validating the theoretical three-stage training dynamics.
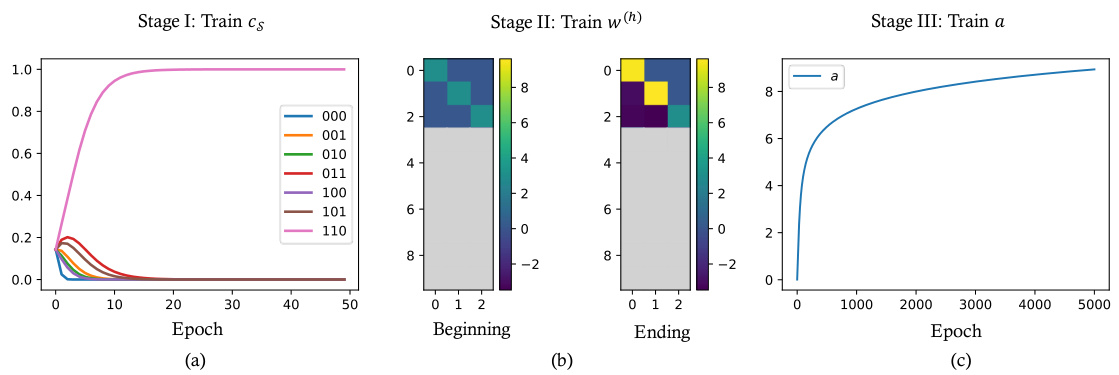
This figure shows the training dynamics of a two-attention-layer transformer model during three stages. Stage I shows the evolution of the FFN layer parameters, where the parameter corresponding to the optimal information set S* dominates exponentially. Stage II shows how the first attention layer learns to copy tokens, focusing on the relevant parents selected by the FFN layer. Stage III shows the growth of the second attention layer’s weight, implementing a softmax classifier that compares features learned in Stage II.

This figure shows the training dynamics of the transformer model with three stages. In the first stage, the FFN parameters are trained. In the second stage, RPE weights in the first attention layer are trained. In the third stage, the weight in the second attention layer is trained. The plots show the evolution of the parameters during these three stages.
This figure shows the training dynamics of the transformer parameters during the three-stage training paradigm. The left panel (a) shows the evolution of the ratio of FFN parameters, ps*(t)/ps(t), where ps*(t) represents the parameter for the optimal subset and ps(t) represents any other subsets. The middle panel (b) shows the RPE weights for each head in the first attention layer. The right panel (c) shows the evolution of the scalar parameter ‘a’ in the second attention layer. Each panel corresponds to a training stage.

The figure shows the generalization performance of the trained transformer model to different sequence lengths and prior distributions. The x-axis represents the sequence length (L) ranging from 10 to 1000, and the y-axis represents the validation loss. Different lines represent different values of the concentration parameter α in the Dirichlet prior distribution (α = 0.05, 0.1, and 0.2). The results show a decreasing trend in validation loss as the sequence length increases, demonstrating that the model generalizes well to unseen lengths and is robust to changes in the prior distribution. The pre-training data consisted of sequences with length L = 100 and α = 0.01.
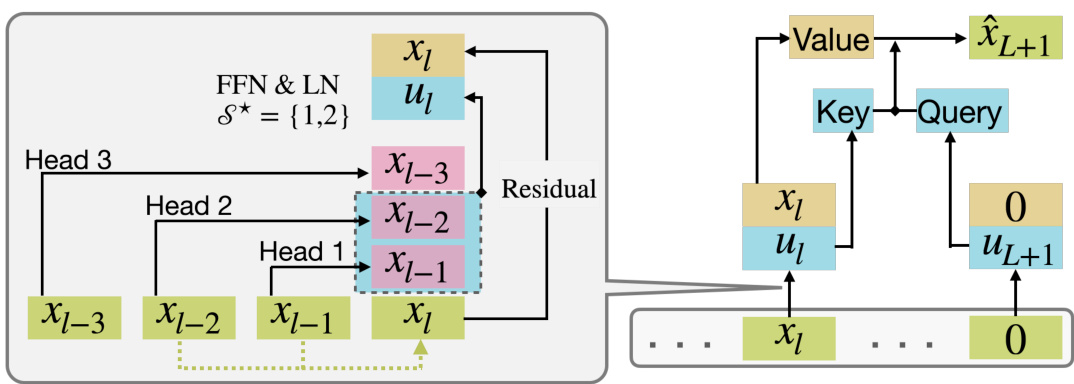
This figure illustrates the Generalized Induction Head (GIH) mechanism implemented by a two-layer transformer model. The first attention layer acts as a copier, copying relevant parent tokens to each position based on the learned information set S*. The feed-forward network (FFN) with normalization then generates feature vectors based on informationally relevant parents. Finally, the second attention layer acts as a classifier comparing these features to predict the output.

This figure shows the training dynamics of a two-layer transformer model during three stages. The first stage trains the feed-forward network (FFN) parameters, the second trains the relative positional embedding (RPE) weights in the first attention layer, and the third trains the weight of the second attention layer. The plots show that the FFN learns to select the relevant parents, the first attention layer learns to copy the selected parents, and the second attention layer learns to perform a generalized induction head mechanism.
More on tables
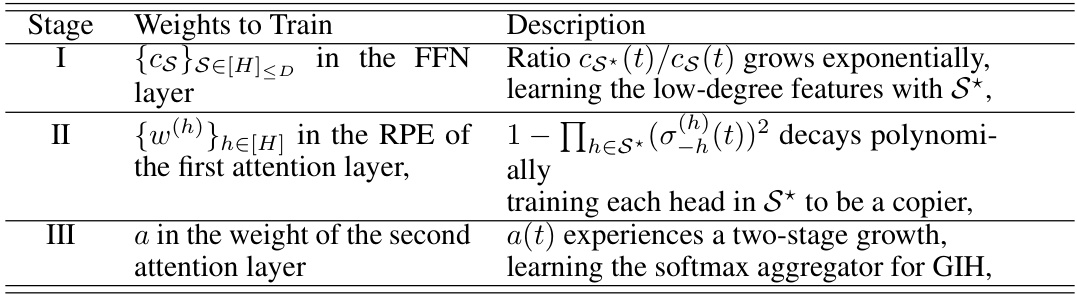
This table summarizes the three-stage training paradigm used in the paper. Each stage focuses on training a specific subset of the model’s weights using gradient flow, while keeping the other weights fixed. Stage I trains the feed-forward network (FFN) to learn the low-degree features, Stage II trains the relative positional embedding (RPE) in the first attention layer to copy relevant parent tokens, and Stage III trains the second attention layer to learn a softmax aggregation, effectively implementing the Generalized Induction Head (GIH) mechanism. The description column provides a summary of the model’s behavior during each training stage.
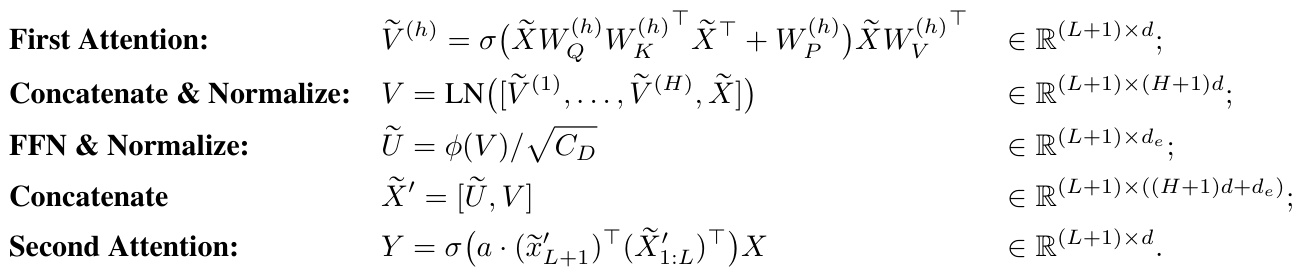
This table describes a three-stage training process for gradient flow in a transformer model. Each stage focuses on training a specific subset of weights while keeping others fixed. Stage I trains the feed-forward network (FFN) layer’s parameters. Stage II trains the relative positional embedding (RPE) weights in the first attention layer. Stage III trains the scalar parameter ‘a’ in the second attention layer. The table provides a description of the dynamics and behavior in each stage.
Full paper#