Instance-Specific Asymmetric Sensitivity in Differential Privacy

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in differential privacy because it introduces a novel algorithmic framework that significantly improves the accuracy of private estimations. It directly addresses the limitations of existing methods by adapting to dataset hardness, offering substantial improvements in various tasks, including variance calculation and machine learning model evaluation. This opens avenues for developing more efficient and accurate privacy-preserving algorithms.

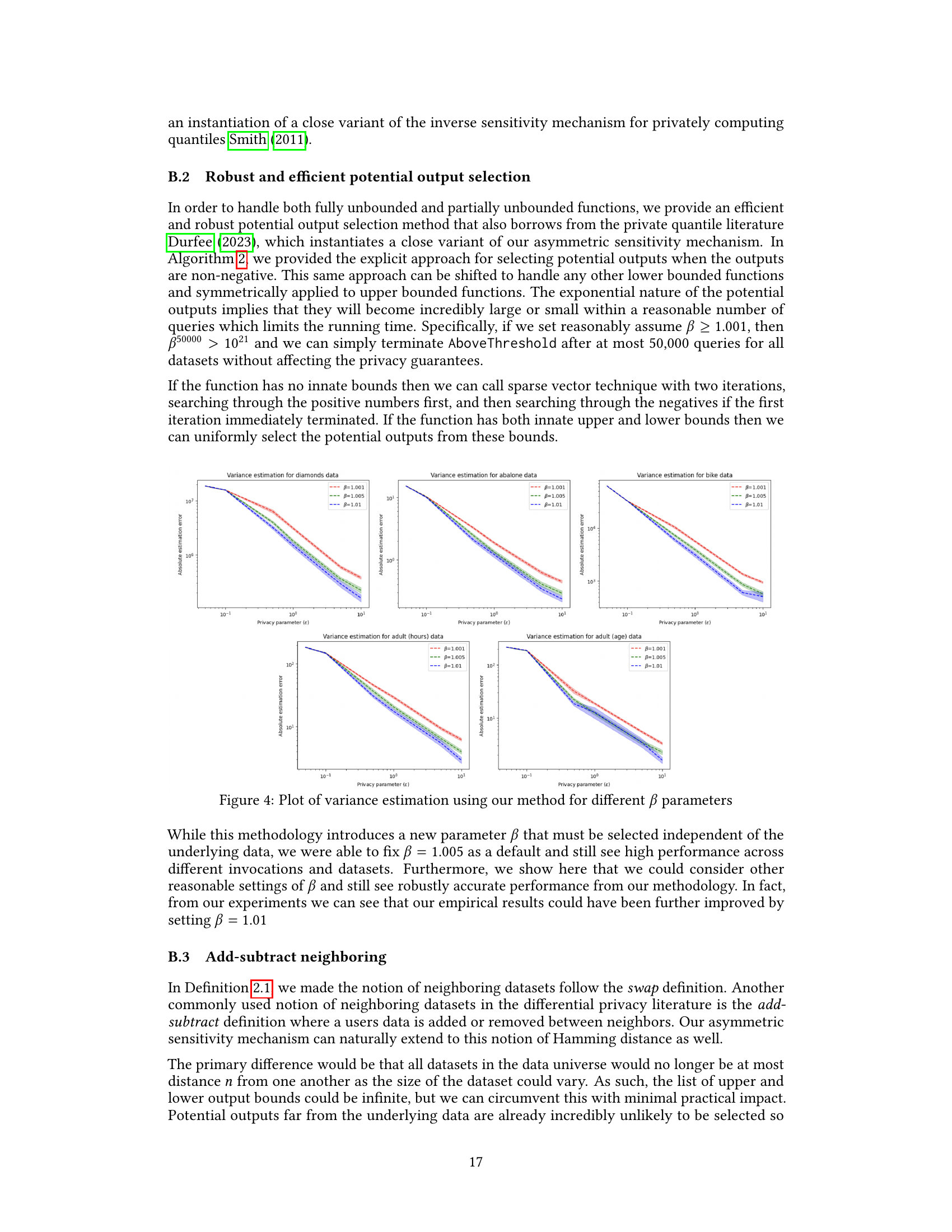
Visual Insights

#

The figure compares three differentially private variance estimation methods: Smooth Sensitivity Mechanism, Inverse Sensitivity Mechanism, and the proposed Asymmetric Sensitivity Mechanism. For several datasets (diamonds, abalone, bike, adult - age and hours worked), the average absolute error of each method is plotted against different privacy parameters (epsilon). Error bars representing 0.9 confidence intervals are included to show the variability of the estimates. The plot demonstrates that the Asymmetric Sensitivity Mechanism consistently outperforms the other two methods across various datasets and privacy levels.

This algorithm details the steps for estimating variance using the asymmetric sensitivity mechanism. It begins by computing approximate lower and upper bounds for variance estimations given a dataset, then utilizes the AboveThreshold algorithm (described elsewhere in the paper) to select an output close to the true variance. The output is scaled by a parameter, β, as part of the algorithm. Lemmas 5.3 and 5.4, referenced in the algorithm, provide the methods for calculating the upper and lower bounds, respectively.

In-depth insights

#

Asymmetric Sensitivity

#

The concept of “Asymmetric Sensitivity” in differential privacy mechanisms addresses the limitation of traditional methods that assume uniform sensitivity across all possible data modifications. It acknowledges that the impact of a single data change can vary significantly depending on the dataset’s characteristics. This asymmetry is particularly relevant in scenarios where adding a data point has a substantially different effect than removing one. The paper proposes a novel approach to leverage this asymmetry, improving the accuracy of differentially private estimations. By recognizing the varying degrees of impact, it aims to reduce unnecessary noise injection, thereby enhancing the utility of the results without compromising privacy guarantees. The proposed “asymmetric sensitivity mechanism” utilizes an iterative sparse vector technique to refine output selection, dynamically adjusting to the dataset-specific sensitivities. This adaptive approach offers a distinct advantage over methods relying on uniform or smooth sensitivity, providing a more nuanced and efficient solution for differentially private data analysis. The theoretical and empirical results strongly support the benefits of this asymmetry-aware method, particularly for problems with inherent asymmetries in their sensitivities like variance calculation or machine learning model evaluation.

Sparse Vector Technique

#

The sparse vector technique, as discussed in the context of differential privacy, offers an efficient approach to address the challenge of privacy-preserving data analysis. Its core idea is to iteratively query a dataset, each time adding carefully calibrated noise based on the query’s sensitivity. If a query’s result, plus added noise, surpasses a dynamically adjusted threshold, the process halts, returning a differentially private response. This mechanism cleverly balances utility and privacy by avoiding the need to know the global sensitivity of all possible queries in advance. This makes it particularly valuable when dealing with high-dimensional datasets or complex queries where calculating global sensitivity is computationally infeasible or prone to overestimation, which could lead to excessive noise addition. However, the sparse vector technique’s efficacy is intrinsically tied to the characteristics of the queries; its performance can be significantly enhanced when the queries are monotonic, meaning that their outputs are consistently increasing or decreasing across neighboring data points. This monotonicity facilitates tighter control over the accumulation of noise, leading to more accurate and private results. While effective, it’s important to note that the sparse vector technique introduces bias. The inherent randomness and iterative nature of the method will skew the most probable outputs, potentially affecting accuracy. The success of the technique is dependent upon this bias-variance tradeoff, which is influenced by the choice of noise distribution, the nature of the queries, and the data itself. Understanding the limitations and inherent bias of this method is crucial for responsible and accurate application in differential privacy schemes.

Variance Estimation

#

The section on variance estimation is crucial as it demonstrates a practical application of the proposed asymmetric sensitivity mechanism. It highlights the method’s effectiveness in handling the bias-variance tradeoff inherent in differentially private variance calculations. The authors show that their method significantly outperforms existing approaches, particularly when dealing with asymmetric sensitivities, which are common in real-world datasets. Efficient implementation details are provided, focusing on the computation of upper and lower bounds and the runtime complexity. The empirical evaluation on various datasets strongly supports the theoretical claims, showing substantial accuracy improvements with varying privacy parameters. The authors address the challenge of unbounded data, a common issue in variance estimation, showcasing how their approach naturally handles this scenario. Overall, this section provides compelling evidence of the proposed method’s superiority in accurately and privately estimating variance, serving as a strong case study for its broader applicability.

Model Evaluation

#

The section on ‘Model Evaluation’ would be crucial for assessing the practical utility of differentially private machine learning models. It should present a rigorous and thorough evaluation across various metrics, including commonly used machine learning performance metrics like cross-entropy loss (classification), mean squared error (MSE), and mean absolute error (MAE) (regression). The discussion must analyze how the proposed asymmetric sensitivity mechanism impacts these metrics, comparing its performance against other methods like the inverse sensitivity mechanism and smooth sensitivity. Key aspects to cover are the accuracy trade-offs at different privacy levels (epsilon), the impact of asymmetry on variance reduction, and how the method handles unbounded data. The evaluation should be conducted on a diverse set of datasets (tabular, image) and model types (linear, deep learning), focusing on both classification and regression tasks. A compelling model evaluation would demonstrate practical advantages, highlighting instances where the proposed method significantly improves accuracy while maintaining rigorous privacy guarantees.

Unbounded Data

#

The concept of handling unbounded data in differential privacy is crucial because many real-world datasets lack inherent bounds. Traditional methods often struggle with unbounded data, as they rely on pre-defined sensitivity parameters. This paper addresses this limitation by breaking the assumption of unbiased mechanisms used in prior approaches. By leveraging a bias-variance trade-off, the authors propose an asymmetric sensitivity mechanism that effectively handles unbounded data. This is achieved through modifications to the inverse sensitivity metric, which now reflects both positive and negative distances, enabling the sparse vector technique to naturally navigate potentially unbounded data. This approach is theoretically justified and empirically validated, demonstrating its effectiveness in scenarios where traditional methods fail. The asymmetric nature of the approach is key, as it allows the algorithm to adapt to data irregularities and avoid the issues associated with using fixed, data-independent sensitivity parameters. Furthermore, the authors’ method provides asymptotic utility guarantees superior to existing techniques for unbounded data.

More visual insights

#

More on figures

The figure compares three different differentially private methods for estimating cross-entropy loss: Smooth Sensitivity Mechanism, Inverse Sensitivity Mechanism, and Asymmetric Sensitivity Mechanism. The plots show the average absolute error for each method across four different datasets (Adult, Diabetes, MNIST, CIFAR) at various privacy parameters (epsilon). Error bars representing 0.9 confidence intervals are included. The results demonstrate the superior accuracy of the Asymmetric Sensitivity Mechanism, especially at higher privacy parameters (smaller epsilon values).

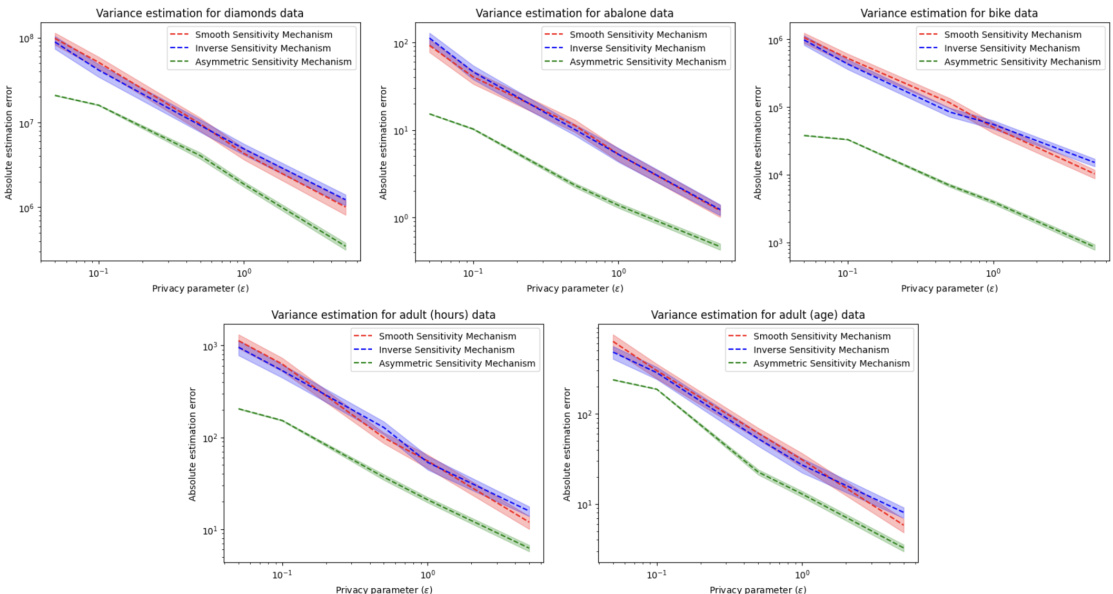
The figure compares three differentially private variance estimation methods (Smooth Sensitivity Mechanism, Inverse Sensitivity Mechanism, and Asymmetric Sensitivity Mechanism) across various privacy parameters (epsilon). For each privacy setting, 1000 data points were sampled, and each mechanism was run 100 times. The plots show the average absolute error, along with 90% confidence intervals, for each method across four different datasets: diamonds, abalone, bike, and adult (age and hours). The results demonstrate that the Asymmetric Sensitivity Mechanism consistently outperforms the other two methods in terms of accuracy, especially at higher privacy levels.

This figure compares three methods for estimating variance with differential privacy: Smooth Sensitivity Mechanism, Inverse Sensitivity Mechanism, and Asymmetric Sensitivity Mechanism. The plots show the average absolute estimation error for each method across a range of privacy parameters (ε). For each privacy parameter, 1000 data points were sampled from a dataset, and each method was run 100 times. Error bars represent 0.9 confidence intervals. The Asymmetric Sensitivity Mechanism consistently demonstrates lower error compared to the other methods.

The figure compares three different methods (Smooth Sensitivity Mechanism, Inverse Sensitivity Mechanism, and Asymmetric Sensitivity Mechanism) for estimating variance under differential privacy. For various privacy parameters (epsilon), the average absolute error of each method is shown, based on 100 trials with 1000 datapoints sampled from the dataset for each trial. The plots visualize the performance of the methods for estimating variance, showing how the error varies with different privacy levels and comparing the effectiveness of each method.

The figure compares three methods for estimating variance under differential privacy: Smooth Sensitivity Mechanism, Inverse Sensitivity Mechanism, and Asymmetric Sensitivity Mechanism. For each privacy parameter (epsilon), 1000 data points were sampled from five different datasets (diamonds, abalone, bike, adult (hours), adult (age)). Each mechanism was run 100 times for each sample, and the average absolute error was plotted with 90% confidence intervals. The plot shows that the Asymmetric Sensitivity Mechanism consistently outperforms the other two methods across all datasets and privacy parameters.

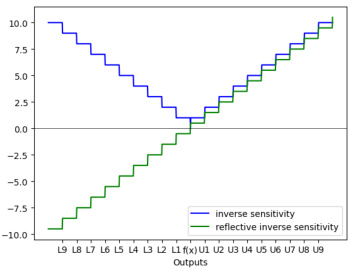
This figure provides a visualization of the inverse sensitivity and reflective inverse sensitivity, which are key concepts in the paper’s proposed asymmetric sensitivity mechanism. It uses step functions based on upper and lower output bounds to illustrate these sensitivities for a scenario with perfectly symmetric sensitivities. The figure serves as a visual aid to help readers grasp the concepts before a more detailed mathematical explanation in a later section.

This figure compares the probability density functions (PDFs) of the Inverse Sensitivity Mechanism (ISM) and the Asymmetric Sensitivity Mechanism (ASM) under the condition of perfectly symmetric sensitivities. It shows how the ASM, through its iterative nature, introduces a slight bias resulting in a more concentrated distribution around the true output (f(x)). The difference is subtle in this symmetric case, but highlights a key difference between the two methods.

This figure compares the probability density functions (PDFs) of the inverse sensitivity mechanism (ISM) and the asymmetric sensitivity mechanism (ASM) when the sensitivities are asymmetric. The ASM’s PDF shows a higher concentration of probability mass around the true output (f(x)) compared to the ISM, indicating that it better handles asymmetric sensitivities.

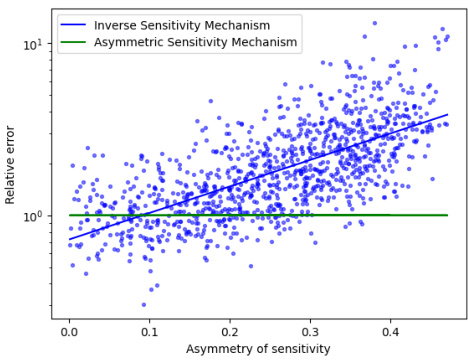
This figure shows the relationship between the relative error of the inverse sensitivity mechanism and the asymmetric sensitivity mechanism and the asymmetry of sensitivities. The x-axis represents the asymmetry of sensitivities (a metric defined in the paper), and the y-axis shows the ratio of the absolute errors of the two methods. The plot indicates that as the asymmetry of sensitivities increases, the relative error of the asymmetric sensitivity mechanism decreases compared to the inverse sensitivity mechanism, suggesting that the proposed method is more advantageous when sensitivities are asymmetric.

Full paper

#