Treeffuser: probabilistic prediction via conditional diffusions with gradient-boosted trees

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it introduces Treeffuser, a novel method for probabilistic prediction on tabular data that addresses the limitations of existing methods. Its non-parametric nature and efficiency make it highly relevant to various fields dealing with uncertain data, paving the way for more accurate and reliable predictions in diverse applications. Furthermore, Treeffuser’s open-source nature promotes wider adoption and collaboration within the research community.

Visual Insights

#

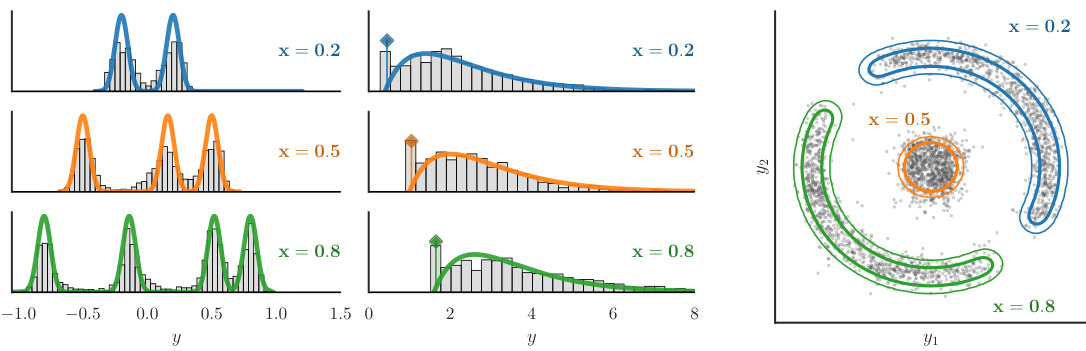
This figure shows examples of how Treeffuser, a probabilistic prediction method, performs on three different types of data distributions: multimodal, inflated, and multivariate. The left column shows histograms of samples generated by Treeffuser for different values of the input variable x. The middle column shows the true densities of the distributions. The right column shows a combined view across all values of x and for all three scenarios. The figure demonstrates that Treeffuser successfully captures the complexity and variability of the underlying distributions across all three scenarios, accurately reflecting the true densities.

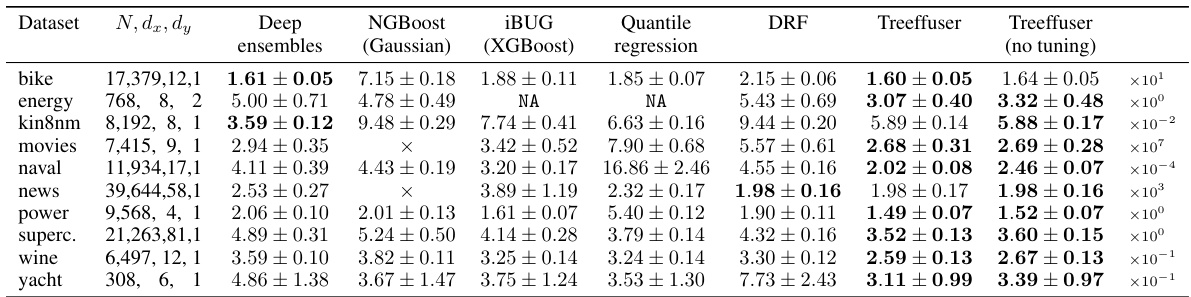
This table compares the continuous ranked probability score (CRPS) of Treeffuser against several other methods across various datasets. Lower CRPS values indicate better performance. The table includes standard deviations calculated using 10-fold cross-validation. Treeffuser consistently outperforms other methods, even without hyperparameter tuning, demonstrating its accuracy and ease of use.

In-depth insights

#

Treeffuser: A Deep Dive

#

Treeffuser, as a novel probabilistic prediction model, presents a compelling approach for handling tabular data. Its core innovation lies in the unique combination of conditional diffusion models and gradient-boosted trees. This hybrid architecture leverages the strengths of both: diffusions’ power to capture complex distributions and trees’ efficiency and robustness in handling tabular data, resulting in a model that’s both flexible and accurate. Treeffuser effectively addresses the limitations of parametric probabilistic methods by providing non-parametric estimations. Furthermore, its efficiency is notable; it can learn well-calibrated predictive distributions efficiently, showcasing its applicability to large real-world datasets. The use of gradient-boosted trees further simplifies the training process, making it more accessible to practitioners. The application to inventory allocation under uncertainty highlights the practical value and versatility of the Treeffuser model.

Conditional Diffusion

#

Conditional diffusion models offer a powerful approach to probabilistic modeling by combining the flexibility of diffusion models with the ability to incorporate conditioning information. They elegantly address the challenge of generating samples from complex, conditional distributions, overcoming limitations of traditional methods that often rely on restrictive assumptions about the underlying data. By learning the score function, which represents the gradient of the log probability density, conditional diffusion models can accurately capture intricate dependencies between variables, even in the presence of high dimensionality or non-linear relationships. The use of gradient-boosted trees for score estimation enhances the robustness and efficiency of these models, making them particularly well-suited for tabular data where trees excel. A key advantage is the non-parametric nature, eliminating the need for strong distributional assumptions. However, the computational cost of sampling from these models can be significant, particularly with high dimensional outputs, posing a limitation to consider in applications with real-time constraints. Future research could focus on developing more computationally efficient sampling techniques to mitigate this limitation while retaining the accuracy and flexibility of the conditional diffusion approach.

GBT Score Estimation

#

In estimating the score function within a diffusion model using gradient-boosted trees (GBTs), a crucial challenge lies in handling the high dimensionality and complexity of the score. GBTs excel at handling tabular data and can efficiently approximate complex functions. The approach likely involves training separate GBTs for each dimension of the score, leveraging the tree-based structure to capture non-linear relationships and interactions among features. A key consideration is the choice of loss function, which impacts the GBT’s convergence speed and the accuracy of the score estimation. Mean squared error (MSE) is a common choice, but other options sensitive to the tails of the distributions might improve the score’s accuracy, particularly if the target distributions have heavy tails. The training process requires careful consideration of hyperparameters, such as tree depth, learning rate, and regularization strength, to balance model complexity and generalization performance. Effective techniques for hyperparameter tuning, such as cross-validation or Bayesian optimization, are essential to achieving optimal GBT performance. Furthermore, the computational cost of training multiple GBTs needs to be addressed, potentially employing parallelization techniques to improve efficiency. Finally, the overall effectiveness relies heavily on the expressiveness of GBTs to capture the score function’s nuances, and it’s essential to evaluate the quality of the estimated score via metrics that align with diffusion model performance criteria.

Treeffuser Limitations

#

The heading ‘Treeffuser Limitations’ would ideally discuss the shortcomings of the proposed probabilistic prediction method. Nonparametric nature, while offering flexibility, can lead to higher computational costs, especially for complex datasets. The reliance on conditional diffusion models, while powerful, introduces the inherent limitation of potential slow training times. Additionally, the approach’s applicability to discrete response variables is limited, although the authors might explore handling this with appropriate transformations. Another aspect is the lack of closed-form density, necessitating the use of a computationally expensive SDE solver, impacting the speed of generating samples for tasks such as risk assessment or uncertainty quantification. Finally, the model’s sensitivity to hyperparameter tuning could influence the performance and increase the complexity of use. Addressing these limitations is crucial for wider adoption and improved reliability in diverse applications.

Future Research

#

Future research directions stemming from this work could explore several promising avenues. Improving the efficiency of the sampling process is crucial, potentially through techniques like progressive distillation or consistency models, which could substantially enhance the scalability of Treeffuser for larger datasets. Addressing the limitation of handling only continuous data by developing extensions for discrete or count data would broaden the applicability of the model. Further investigation into the theoretical properties of Treeffuser, such as the convergence rates of the score estimation procedure and the sensitivity of its performance to model hyperparameters, would strengthen the theoretical foundations. Exploring alternative tree-based models beyond gradient-boosted trees, or even employing neural networks as the score function approximator, could reveal further performance gains or improved flexibility. Finally, applying Treeffuser to a broader range of real-world applications and rigorously evaluating its performance against a wider set of benchmark methods, particularly in high-dimensional settings, would establish its practical utility and robustness.

More visual insights

#

More on figures

This figure shows the results of Treeffuser on three different complex distributions: a multimodal response with varying components, an inflated response with shifting support, and a multivariate response with dynamic correlations. For each scenario, Treeffuser generates samples from the target conditional distribution, demonstrating its ability to capture the complexity of arbitrarily complex conditional distributions that vary with the input variable x. The plots visually compare the samples generated by Treeffuser with the actual true densities of the target distributions.

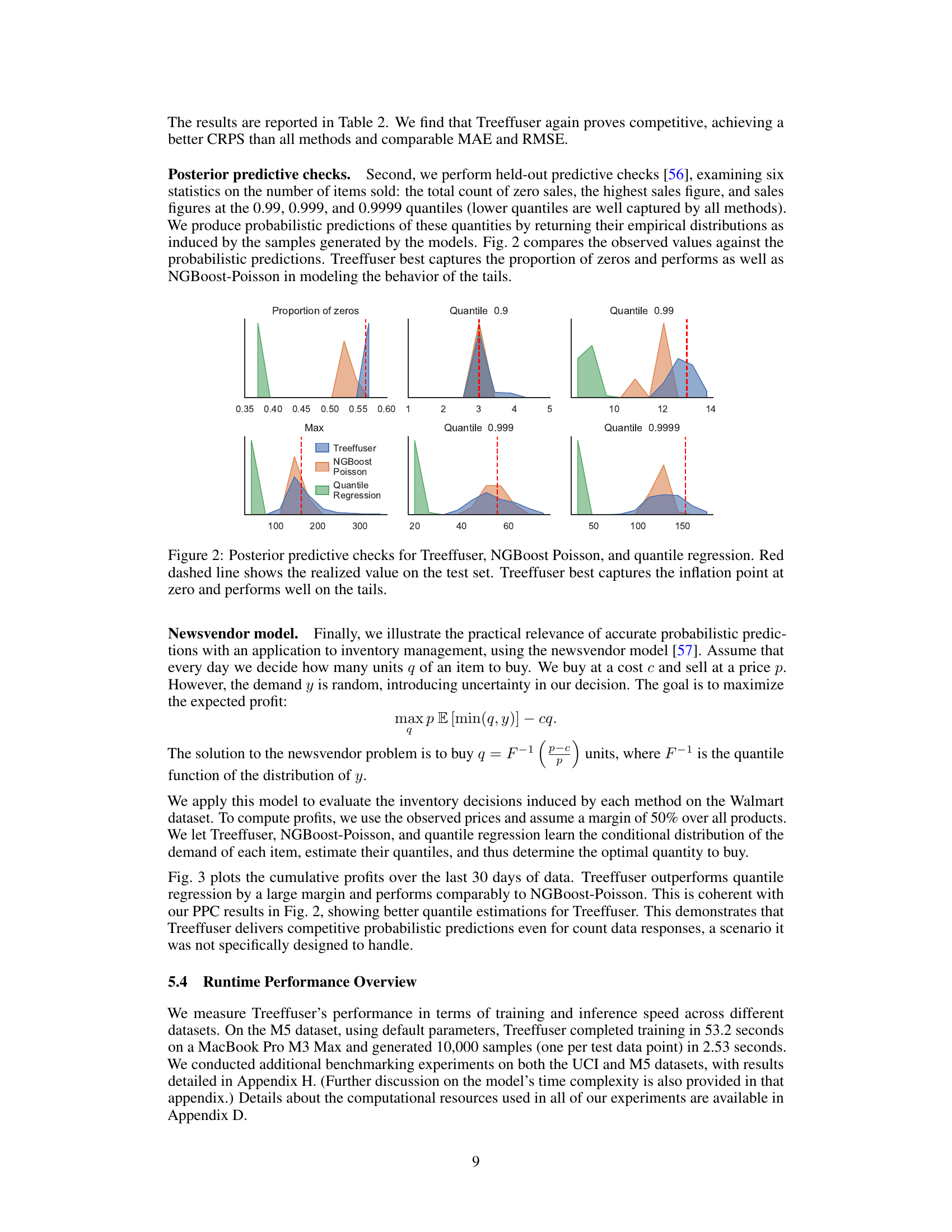
This figure shows the cumulative profits over 30 days for three different models used for inventory management: Treeffuser, NGBoost-Poisson, and Quantile Regression. Both tuned and default hyperparameters are shown for each model. The graph demonstrates that Treeffuser consistently outperforms the other models, achieving significantly higher cumulative profits, highlighting the advantages of using Treeffuser for making more accurate probabilistic predictions in this specific context.

This figure compares samples generated by Treeffuser with the true probability density functions for three different scenarios. Each scenario involves a different type of complex conditional distribution: a multimodal response with varying components, an inflated response with shifting support, and a multivariate response with dynamic correlations. The figure shows that Treeffuser accurately captures the complexity of each distribution, demonstrating its ability to learn and sample from arbitrarily complex conditional distributions.

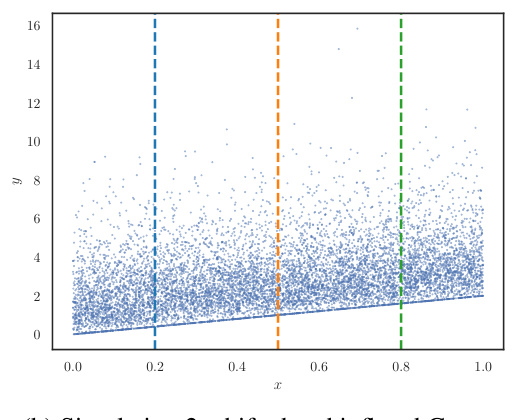
This figure demonstrates the ability of Treeffuser to model complex conditional distributions. It shows three scenarios: a multimodal response, an inflated response, and a multivariate response. For each scenario, Treeffuser accurately captures the true density of the response variable (y) given different values of the input variable (x), even when the true densities are multimodal, skewed, or exhibit dynamic correlations. This highlights Treeffuser’s flexibility and nonparametric nature.

This figure visualizes the performance of Treeffuser in capturing complex conditional distributions. It presents three different scenarios, each with multiple values of x, showcasing how Treeffuser generates samples (yx) that closely match the true probability density functions (PDFs). The scenarios illustrate Treeffuser’s ability to handle multimodal distributions, distributions with shifting support, and multivariate distributions with dynamic correlations. This demonstrates the model’s non-parametric nature and its capacity for accurately estimating complex relationships in data.

This figure shows the relationship between the size of the training dataset and the time it takes to train the Treeffuser model. The x-axis represents the number of samples in the dataset, and the y-axis represents the mean training time in seconds. Error bars indicate the variability in training time across multiple runs. The figure demonstrates that the training time scales linearly with the size of the dataset, indicating that Treeffuser is computationally efficient, especially on large datasets.

More on tables

This table compares the performance of different probabilistic prediction models on the Walmart sales forecasting task. The metrics used are CRPS (Continuous Ranked Probability Score), RMSE (Root Mean Squared Error), and MAE (Mean Absolute Error). Lower values indicate better performance. The table shows that Treeffuser achieves the lowest CRPS, indicating the best probabilistic predictions, comparable to NGBoost Poisson. Deep ensembles achieve the lowest RMSE and MAE, suggesting the best point predictions.

This table compares the continuous ranked probability score (CRPS) of various probabilistic prediction methods across several datasets. Lower CRPS values indicate better predictive performance. The table includes results from deep ensembles, NGBoost, IBUG, quantile regression, and DRF, in addition to Treeffuser with and without hyperparameter tuning. Note that some methods failed on certain datasets, and some are not directly applicable to multivariate outcomes. The results show that Treeffuser generally outperforms other methods, even without tuning.

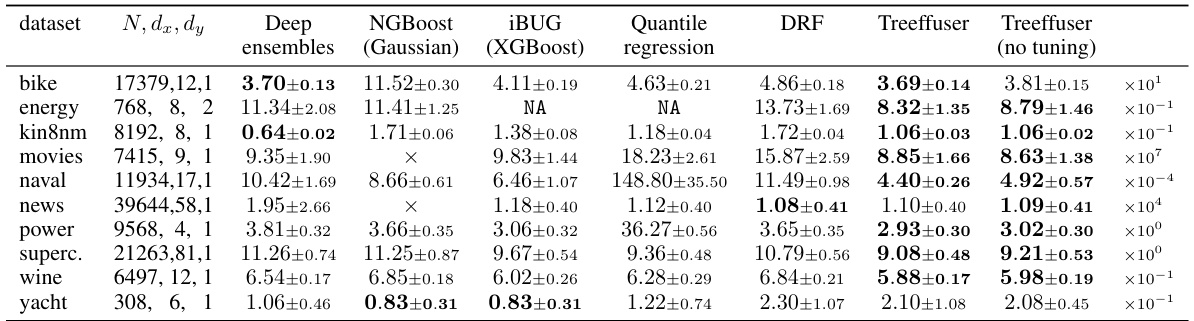
This table compares the continuous ranked probability score (CRPS) of Treeffuser against several other methods for probabilistic prediction on various benchmark datasets. Lower CRPS indicates better performance. The table shows that Treeffuser generally achieves the lowest CRPS, demonstrating superior predictive accuracy. The ’no tuning’ column highlights Treeffuser’s performance even without hyperparameter optimization.

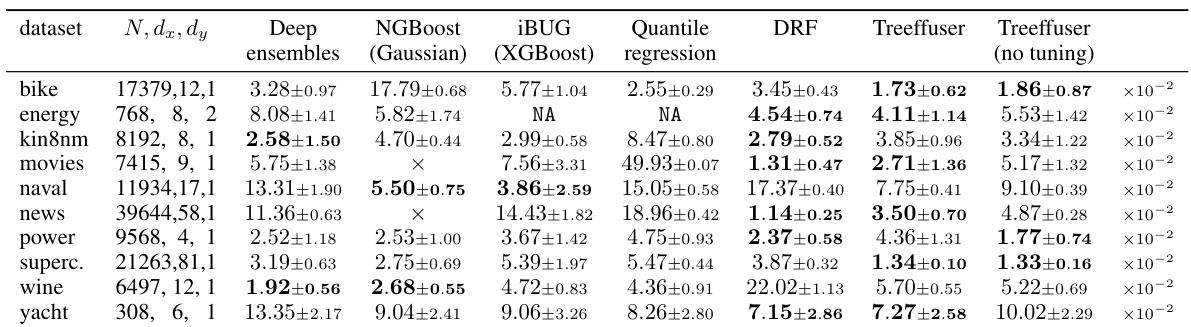
This table presents the Continuous Ranked Probability Score (CRPS) for various datasets and prediction methods, including Treeffuser and several baselines. Lower CRPS values indicate better predictive performance. The table highlights Treeffuser’s superior accuracy, even when using default hyperparameters. The ‘×’ indicates that a method failed to run for a specific dataset, while ‘NA’ shows the method was inapplicable to multivariate outputs. Standard deviations are based on 10-fold cross-validation.

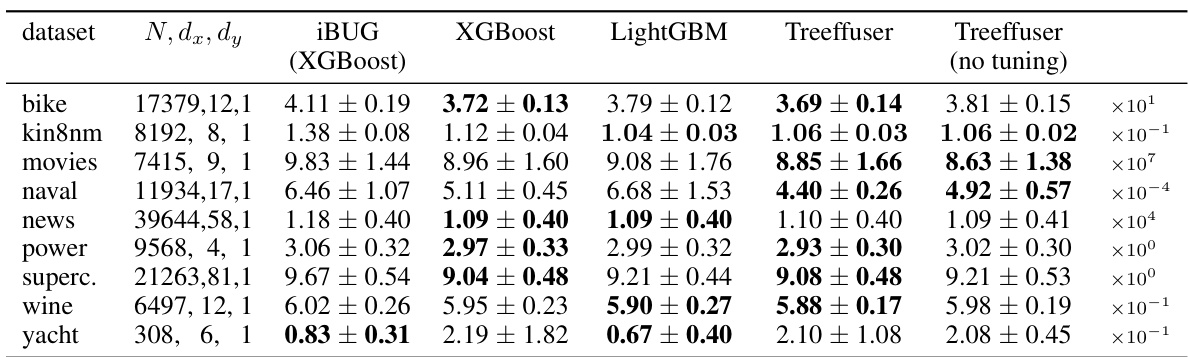
This table presents the continuous ranked probability score (CRPS) for various probabilistic prediction methods across multiple datasets. Lower CRPS values indicate better predictive accuracy. The table includes results from Deep Ensembles (Gaussian), NGBoost (Gaussian), IBUG (XGBoost), Quantile Regression, DRF, Treeffuser (with tuning), and Treeffuser (without tuning). The results demonstrate that Treeffuser generally provides the lowest CRPS values, indicating superior predictive accuracy compared to the other methods, even when using default hyperparameters. The table also shows that Treeffuser handles both univariate and multivariate responses well, though some methods did not apply to multivariate outputs.

This table compares the continuous ranked probability score (CRPS) achieved by Treeffuser with and without noise scaling across various datasets. The results demonstrate that noise scaling is crucial for Treeffuser’s performance, as the model without noise scaling fails to produce meaningful results.

This table presents the results of the continuous ranked probability score (CRPS) for different probabilistic prediction methods across various datasets. Lower CRPS values indicate better performance. The table includes standard deviations calculated via 10-fold cross-validation and highlights the top-performing methods for each dataset. Treeffuser consistently outperforms other methods, even without hyperparameter tuning.

Full paper

#