↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Differentially private (DP) machine learning faces challenges with high-dimensional data, especially in models using large embedding tables that generate sparse gradients. Existing DP optimization methods struggle with the computational cost and accuracy limitations in such scenarios, hindering the development of privacy-preserving AI systems. This paper addresses these issues by focusing on the sparsity of individual gradients.
The researchers developed new DP algorithms that leverage the gradient sparsity. They achieved almost optimal accuracy rates for convex optimization and near-optimal dimension-independent rates for near-stationary points in nonconvex settings. This breakthrough was made possible through a novel analysis of bias reduction and randomly-stopped biased SGD algorithms. This work provides more efficient and scalable methods for training large-scale private AI models, advancing the field of privacy-preserving machine learning.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in differential privacy and machine learning. It offers near-optimal algorithms for handling sparse gradients, a common challenge in large embedding models. The dimension-independent rates achieved are a significant improvement, opening doors for more efficient and scalable private AI.
Visual Insights#

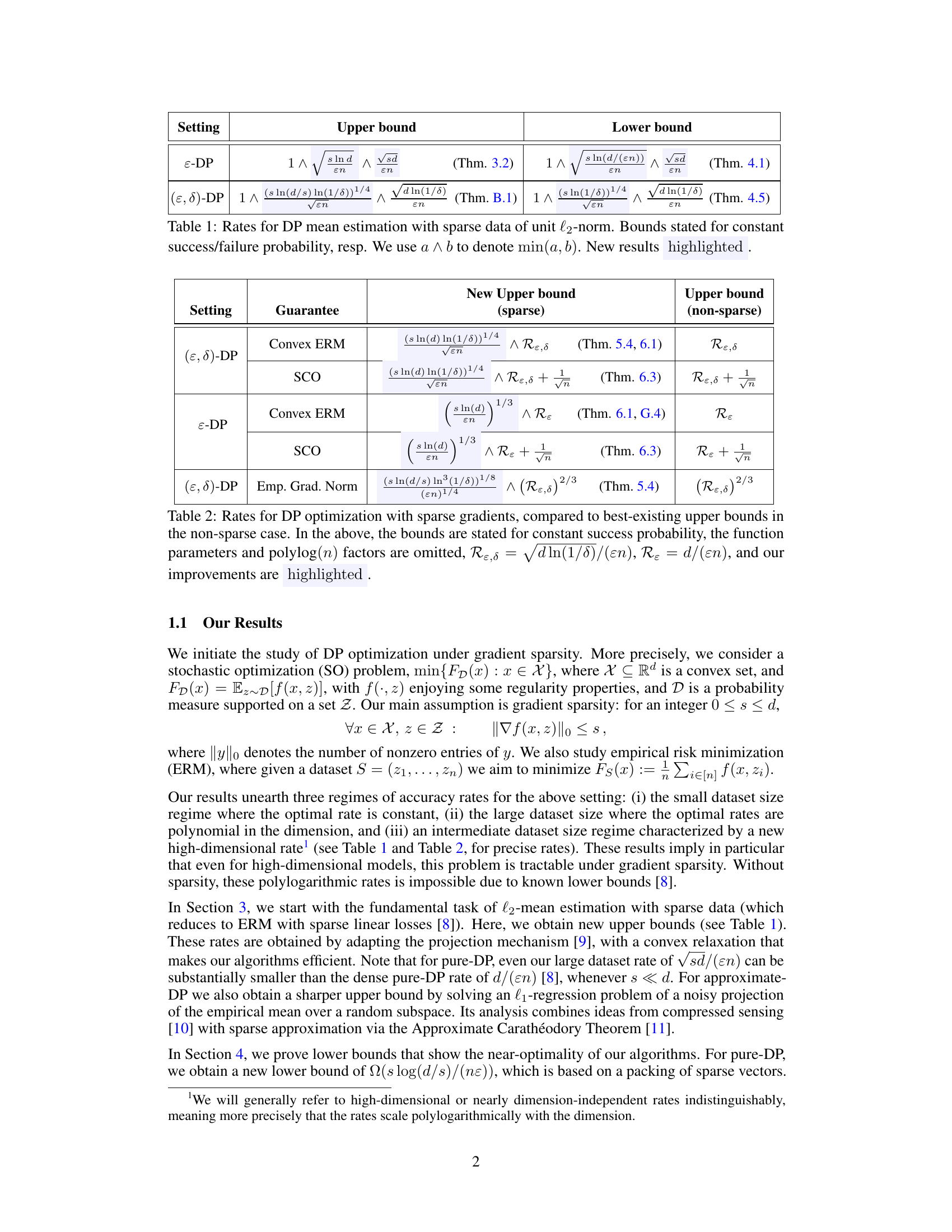
This table presents upper and lower bounds for differentially private (DP) mean estimation with sparse data. It shows the rates of convergence for both pure-DP (ε-DP) and approximate-DP ((ε, δ)-DP) mechanisms, highlighting the dependence on the sparsity level (s), dimension (d), privacy parameters (ε, δ), and sample size (n). New results from the paper are emphasized.
In-depth insights#
Sparse DP Optim.#
Sparse DP Optimization is a fascinating area bridging the need for privacy (Differential Privacy or DP) and efficiency in machine learning, particularly when dealing with high-dimensional data. The core challenge lies in balancing the noise injection inherent in DP with computational constraints. Sparsity, meaning many model parameters are zero, significantly reduces computational cost. The combination of these areas focuses on developing algorithms that achieve provable privacy guarantees while maintaining efficiency by leveraging sparsity in gradients or model parameters during the optimization process. Key aspects include designing specialized DP mechanisms that effectively handle sparse data, establishing theoretical guarantees on the resulting privacy and utility trade-off, and developing algorithms that scale to very large datasets often encountered in applications involving massive embedding tables. Successful approaches often involve techniques from compressed sensing, advanced optimization methods, and careful privacy accounting. Major contributions in this field could involve novel DP mechanisms tailored to sparse data, sharper bounds on the privacy-utility trade-off, or efficient algorithms with improved convergence rates.
New Algorithmic Bounds#
A research paper section on “New Algorithmic Bounds” would ideally present novel algorithmic advancements for solving computational problems, focusing on improved efficiency or accuracy. The core of the section would likely involve presenting new upper and lower bounds on the algorithm’s performance. Upper bounds would demonstrate the algorithm’s maximum resource consumption (time, space, etc.), while lower bounds would establish fundamental limits on the best possible performance achievable by any algorithm solving the same problem. A strong paper would show a tight gap between upper and lower bounds, indicating the near-optimality of the proposed algorithm. The section should also discuss the techniques used to derive the bounds, highlighting novel approaches or significant improvements over existing methods. Proofs or proof sketches are essential for establishing the validity of the bounds. The analysis might also consider various problem parameters, providing detailed insights into how the bounds scale with different inputs. For example, it could explore how the computational complexity is affected by the dimension of input data or the level of sparsity in the problem’s structure. Ultimately, a compelling “New Algorithmic Bounds” section would clearly demonstrate the superiority of the new algorithms and enhance the overall contribution of the research paper. It might conclude by suggesting avenues for future work based on the obtained bounds, perhaps identifying open problems or areas for improvement.
Bias Reduction in SGD#
In stochastic gradient descent (SGD), bias reduction is crucial for reliable convergence, especially when dealing with differentially private (DP) settings. Standard SGD methods, particularly when combined with DP mechanisms, often introduce bias in gradient estimates. This bias, if left unaddressed, can significantly hinder the algorithm’s ability to find optimal solutions or even converge to reasonable near-optimal points. The paper addresses this challenge by introducing a novel bias reduction technique using a carefully crafted mechanism involving randomly-stopped biased SGD and a telescopic estimator. This approach exploits the sparsity of gradients in the application, making the bias reduction method particularly effective in high-dimensional settings, typical in large embedding models. The introduction of random batch sizes plays a pivotal role in mitigating bias, but necessitates sophisticated techniques to control the variance and account for the probabilistic nature of the method’s execution and privacy budget. The resulting algorithm achieves nearly dimension-independent convergence rates, showcasing a significant improvement over existing DP optimization techniques.
High-Dim. Rate Regime#
The High-Dimensional Rate Regime in differentially private (DP) optimization with sparse gradients is a critical area of study. This regime emerges when the dataset size is neither too small (where rates are constant) nor overwhelmingly large (polynomial dependence on dimension). The key insight is that sparsity significantly alters the optimal convergence rates, moving them from a strong dependence on dimensionality (as seen in dense DP optimization) to a much weaker polylogarithmic dependence or even dimension independence in some cases. This improvement is particularly striking for high-dimensional settings where the number of features far exceeds the sample size. The sparse algorithms’ success stems from leveraging the sparsity structure to perform efficient updates and projections into carefully chosen subspaces, leading to near-optimal rates, which are often nearly dimension-independent. However, lower bounds demonstrate that this advantage is not unlimited; even in the high-dimensional regime, the impact of sparsity is subject to mathematical limits. The theoretical results highlight the potential of exploiting the sparsity inherent in large-scale machine learning applications like embedding models to achieve efficient and privacy-preserving optimization.
Future Research Gaps#
Future research could explore several avenues. Extending the theoretical analysis to non-convex settings is crucial, as many real-world applications involve non-convex optimization problems. Current high-dimensional rates are nearly optimal for convex problems but may not generalize well to non-convex cases. Another gap lies in developing adaptive algorithms that do not require prior knowledge of gradient sparsity (s); while theoretical results show benefits from sparsity, adaptive methods would make the techniques more practical. Improving the lower bounds for approximate differential privacy would also enhance our understanding of fundamental limitations in this regime, and there is a significant gap in the current high-dimensional analysis of approximate DP mean estimation. Finally, more research could focus on developing efficient and practical algorithms that scale well to large datasets and high-dimensional problems. Specifically, this would involve comparing the empirical performance of the novel algorithm introduced against well-established baselines.
More visual insights#
More on tables

This table compares the upper bounds for differentially private optimization with sparse gradients to existing upper bounds without sparsity. It shows rates for convex and non-convex empirical risk minimization (ERM) and stochastic convex optimization (SCO) under both pure and approximate differential privacy. The table highlights the improvements achieved by the authors’ algorithms, which are nearly dimension-independent in many settings.

This table shows upper and lower bounds for differentially private (DP) mean estimation with sparse data. The bounds are presented for both pure DP (ε-DP) and approximate DP ((ε, δ)-DP) settings. The data is assumed to have unit l2-norm, and the bounds are given for a constant success/failure probability. The table highlights new results achieved by the authors.
Full paper#