↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Fine-tuning large foundation models often struggles with balancing model fitting and robustness. Overly aggressive optimization can lead to overfitting and poor generalization, while insufficient regularization may not adequately constrain the model’s parameters, impacting its robustness to unseen data. Existing methods addressing this challenge either have limitations in their usability or require significant computational overhead.
This paper introduces Selective Projection Decay (SPD), a novel weight decay method that selectively regularizes model parameters based on a carefully designed condition. SPD prioritizes layers with consistent loss reduction and thus constrains those layers exhibiting inconsistent performance. Experimental results on image classification, semantic segmentation, and large language model fine-tuning across various benchmarks demonstrate that SPD significantly improves both in-distribution and out-of-distribution performance, outperforming existing methods in simplicity and effectiveness. The compatibility of SPD with PEFT methods further enhances its applicability to large-scale models.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in deep learning and fine-tuning because it addresses the critical challenge of balancing model fitting and robustness during model adaptation. The proposed SPD method offers a simple yet effective solution to improve generalization and out-of-distribution robustness, significantly impacting the fields of computer vision, natural language processing, and beyond. Its compatibility with PEFT techniques makes it particularly relevant to current research trends involving large language models. The findings open new avenues for developing efficient and robust fine-tuning strategies.
Visual Insights#

This figure illustrates how Selective Projection Decay (SPD) applies regularization differently in full fine-tuning and parameter-efficient fine-tuning (PEFT). In full fine-tuning, SPD constrains the distance between the fine-tuned model’s weights (Wt) and the pre-trained model’s weights (Wo) (||Wt – Wo||2). In PEFT, where only a small set of parameters are updated (∆Wt), SPD focuses on regularizing the change in these parameters (||∆Wt||2). The diagram uses a visual metaphor of containers and springs to represent the model weights and the regularization.

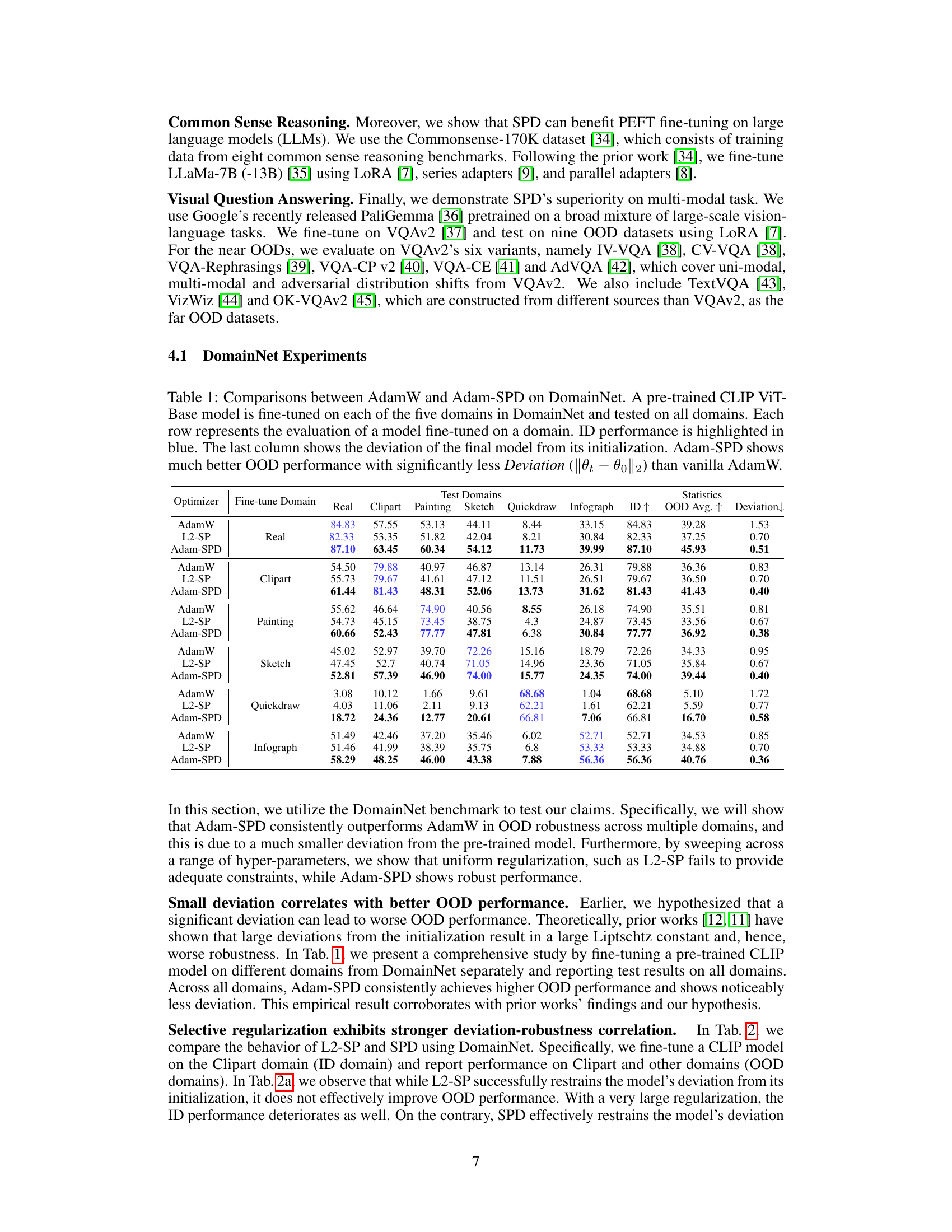
This table compares the performance of AdamW and Adam-SPD optimizers on the DomainNet dataset. A CLIP ViT-Base model was fine-tuned on each of the five DomainNet domains and then tested on all domains. The table shows in-distribution (ID) and out-of-distribution (OOD) performance metrics, highlighting the superior OOD performance of Adam-SPD with significantly lower deviation from the pre-trained initialization.
In-depth insights#
SPD: Selective Decay#
The proposed Selective Projection Decay (SPD) method offers a novel approach to weight decay in the fine-tuning of large foundation models. Instead of applying weight decay uniformly across all layers, SPD selectively applies strong penalties only to layers exhibiting inconsistent loss reduction. This intelligent application prevents unnecessary deviations from the pre-trained initialization, enhancing robustness and generalization. The core of SPD involves a carefully constructed condition (ct) which determines when to impose regularization. This condition is derived from a hyper-optimization perspective, identifying layers where the update direction contradicts consistent loss reduction. The method’s effectiveness stems from selectively restricting the search space for parameters which helps avoid overfitting. Furthermore, SPD incorporates a deviation ratio (rt) to intuitively control regularization strength. By combining layer-specific regularization with an analytical measure of parameter drift, SPD strikes a balance between fitting the fine-tuning data and preserving the benefits of pre-training. The approach’s simplicity is compelling, requiring minimal code additions and computational overhead, while still achieving state-of-the-art results on various benchmarks.
PEFT Integration#
Parameter-Efficient Fine-Tuning (PEFT) methods are crucial for adapting large language models (LLMs) without the computational burden of full fine-tuning. PEFT integration, therefore, focuses on how to seamlessly incorporate PEFT techniques such as LoRA, adapters, and others, into existing training pipelines. This involves carefully considering the interaction between the PEFT modules and the pre-trained model parameters. A key challenge is balancing the benefits of efficient adaptation with maintaining model robustness and performance. The integration strategy should address how PEFT layers are initialized, trained, and updated in conjunction with other parts of the model. Successful integration requires careful design to avoid negative impacts such as catastrophic forgetting or underfitting. For example, strategies to selectively apply PEFT methods or impose regularizations could play an important role in effective integration, addressing the trade-off between efficient parameter updates and preserving pre-trained knowledge. Further research into advanced integration strategies, particularly concerning handling complex architectures or scenarios with limited training data, is highly needed. Finally, a practical consideration is the memory footprint and computational overhead of adding PEFT components, which needs to be carefully balanced with the gains in efficiency.
Robustness Gains#
Analyzing robustness gains in the context of fine-tuning foundation models reveals crucial insights. Improved out-of-distribution (OOD) generalization is a key benefit, suggesting enhanced model adaptability to unseen data. This is particularly important for real-world applications where perfect data matching is unrealistic. Selective regularization techniques seem to be key in achieving these gains, as they prevent overfitting while preserving pre-trained knowledge. The success of selective approaches points towards the importance of a nuanced approach to weight decay, rather than applying uniform penalties across all model parameters. Such a nuanced approach is essential to maintaining pre-trained knowledge while adapting to new data. Moreover, robustness improvements often correlate with smaller deviations from the pre-trained model weights. This relationship suggests a potential trade-off between adaptation and stability, where excessive exploration of the parameter space can sacrifice robustness. The research highlights the potential of parameter-efficient fine-tuning (PEFT) methods in conjunction with selective regularization, demonstrating that robustness gains can be achieved even with minimal parameter updates. Further research is needed to fully explore the interplay between various regularization strategies, model architectures, and data characteristics in achieving robust performance on a broader range of tasks.
Hyperparameter Tuning#
Hyperparameter tuning is crucial for optimizing model performance. Effective strategies must balance exploration and exploitation, carefully navigating the vast parameter space to find settings that yield optimal results. This often involves sophisticated techniques beyond simple grid searches, such as Bayesian optimization or evolutionary algorithms, which leverage prior knowledge and adaptive sampling. Careful consideration of the objective function is paramount, ensuring it accurately reflects the desired performance metric and incorporates relevant regularization terms. Robust validation strategies, employing techniques like cross-validation and nested cross-validation, are essential to prevent overfitting and ensure reliable generalization. Finally, resource management is critical, as tuning can be computationally expensive, requiring careful allocation of time and computing resources. The choice of tuning method should be guided by available resources, problem complexity, and the desired level of optimization.
Future Directions#
Future research could explore adaptive mechanisms for determining the optimal regularization strength for each layer, potentially using reinforcement learning or Bayesian optimization. Another promising avenue is investigating the interaction between SPD and other robust fine-tuning techniques, such as feature normalization or adversarial training, to achieve further improvements in generalization and robustness. The effectiveness of SPD across diverse model architectures and data modalities beyond those tested requires further investigation. Extending SPD to other tasks, such as time-series forecasting or reinforcement learning, could also prove valuable. Finally, a more in-depth theoretical analysis of SPD’s behavior and its relationship to other regularization methods is needed to solidify its foundation and better understand its limitations. Investigating potential biases introduced by the selective regularization process and developing methods to mitigate them would also be a key step towards broader adoption.
More visual insights#
More on tables
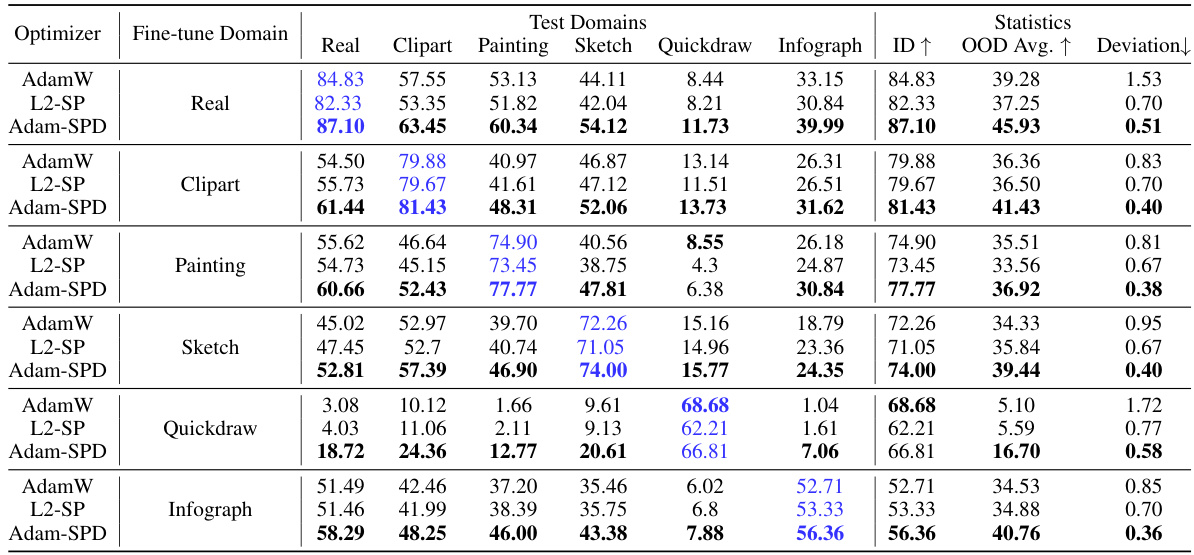
This table compares the performance of AdamW and Adam-SPD optimizers on the DomainNet dataset for image classification. A pre-trained CLIP ViT-Base model was fine-tuned on each of the five DomainNet domains and then evaluated on all domains. The table highlights the in-distribution (ID) and out-of-distribution (OOD) performance of each optimizer, showing Adam-SPD’s superior OOD performance and significantly lower deviation from the initial model weights.

This table compares the performance of L2-SP and Adam-SPD on the DomainNet dataset, focusing on the impact of selective regularization on in-distribution (ID) and out-of-distribution (OOD) robustness. It shows how different hyperparameter settings affect the trade-off between ID and OOD performance, demonstrating the benefits of selective regularization in improving OOD robustness without sacrificing ID performance.
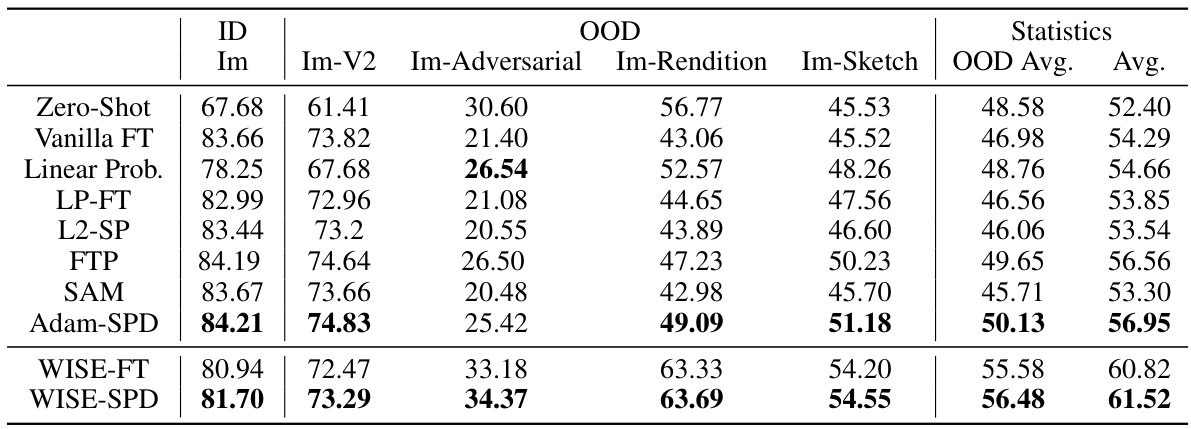
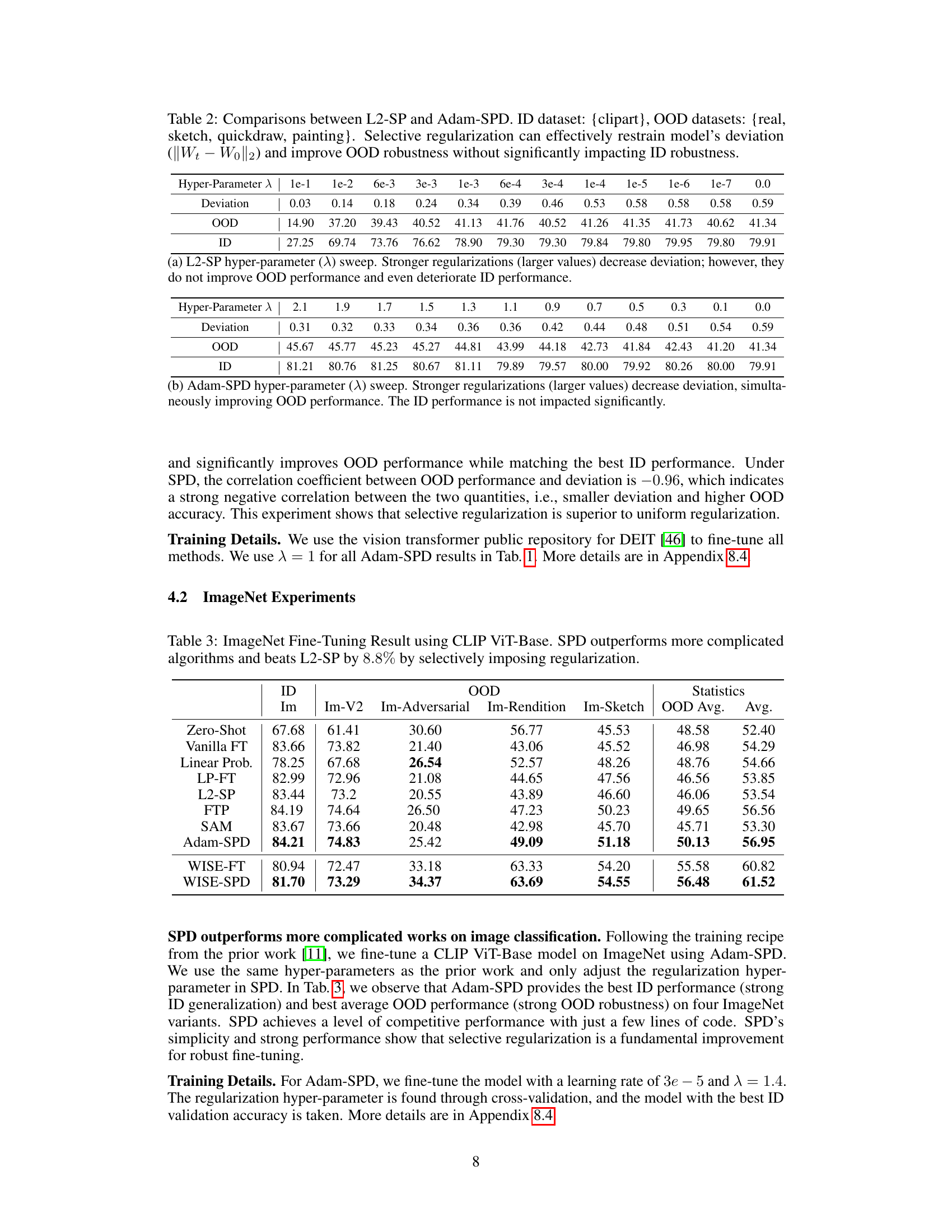
This table presents the ImageNet fine-tuning results using a CLIP ViT-Base model. It compares the performance of various methods, including Adam-SPD, on both in-distribution (ID) and out-of-distribution (OOD) image classification tasks. The metrics used are the average accuracy across multiple OOD datasets (Im-V2, Im-Adversarial, Im-Rendition, and Im-Sketch) and the average accuracy across ID datasets (Im). Adam-SPD demonstrates superior performance compared to other methods, particularly L2-SP, highlighting the effectiveness of selective regularization.
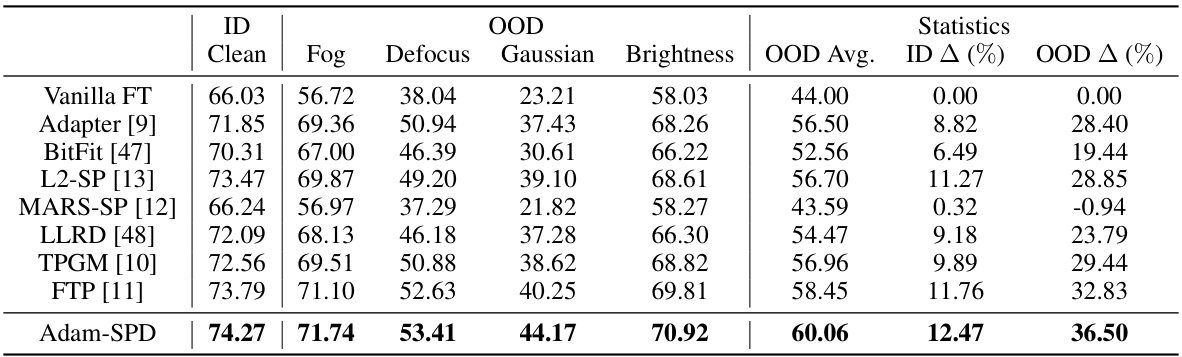
This table presents the results of Pascal Dense Semantic Segmentation experiments. It compares the performance of various methods (vanilla fine-tuning, adapters, BitFit, L2-SP, MARS-SP, LLRD, TPGM, FTP, and Adam-SPD) on the clean PASCAL dataset and several corrupted versions (fog, defocus, gaussian noise, and brightness) using a Swin-Tiny transformer model. The metrics used are mean Intersection over Union (mIoU) for ID (In-distribution) and OOD (Out-of-distribution) performance. The table highlights the improvements in OOD robustness achieved by the Adam-SPD method, outperforming others and showing significant gains compared to vanilla fine-tuning and L2-SP.
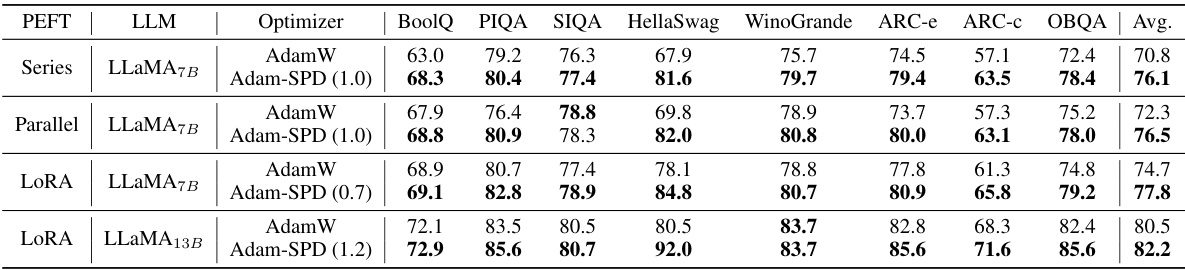
This table presents the results of experiments comparing the performance of different optimizers (AdamW and Adam-SPD) and parameter-efficient fine-tuning (PEFT) methods on eight commonsense reasoning datasets using the LLaMA-7B and LLaMA-13B language models. The results show that Adam-SPD consistently outperforms AdamW across various PEFT methods, highlighting the benefits of selective projection decay for improved performance in this task.

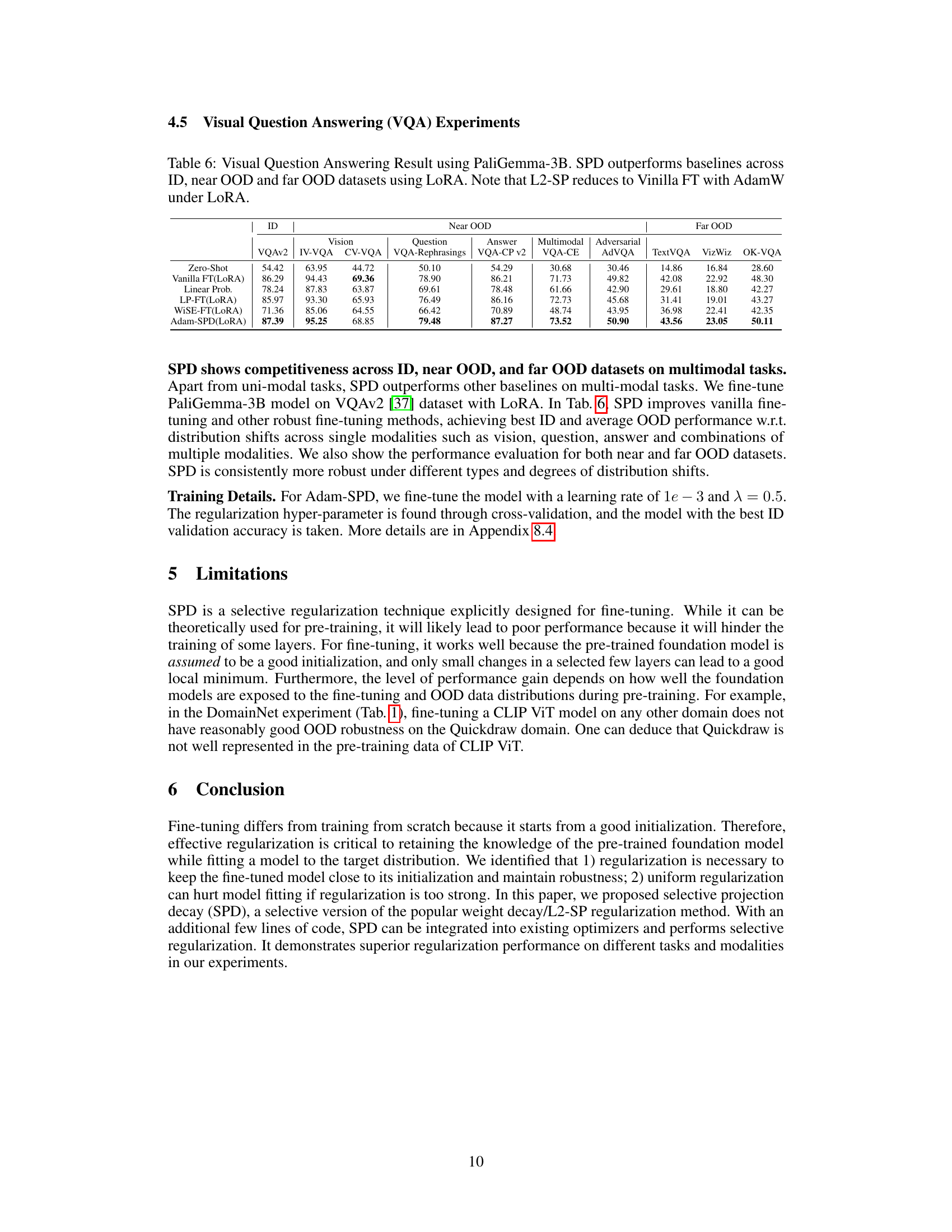
This table presents the results of visual question answering experiments using the PaliGemma-3B model and LoRA. It compares the performance of various fine-tuning methods (Vanilla FT, Linear Prob, LP-FT, WISE-FT, and Adam-SPD) across different datasets representing in-distribution (ID), near out-of-distribution (OOD), and far OOD scenarios. The results highlight Adam-SPD’s superior performance in handling out-of-distribution data.

This table compares the performance of AdamW and Adam-SPD optimizers on the DomainNet dataset. A pre-trained CLIP ViT-Base model is fine-tuned on five different domains, and then tested on all domains. The table shows in-distribution (ID) and out-of-distribution (OOD) accuracy, as well as the deviation of the final model from its initial parameters. The results highlight that Adam-SPD achieves significantly better OOD performance with substantially less deviation from the initial model weights compared to AdamW.
Full paper#